C++ 数据结构之-最小栈(MinStack)
最小栈
最小栈(Min Stack)是一个支持常数时间复杂度获取栈中最小元素的特殊栈数据结构。通常,标准的栈数据结构只支持在常数时间内执行入栈(push)和出栈(pop)操作,但无法在常数时间内获取栈中的最小元素。
最小栈通过在每个栈节点中额外存储一个当前阶段的最小值,从而实现在常数时间内获取最小元素的功能。这意味着无论栈的大小如何,都可以在常数时间内获取栈中的最小值。
最小栈的主要操作包括:
-
入栈(push):将元素压入栈顶,并更新当前最小值。
-
出栈(pop):从栈顶弹出一个元素。
-
获取最小值(getMin):返回栈中的最小元素,即栈顶节点的最小值。
这样,在使用最小栈时,我们可以通过调用 getMin 操作来获取栈中的最小元素,并保持常数时间复杂度。其他与标准栈一致的操作,例如入栈和出栈,仍然可以在常数时间内执行。
使用最小栈的一个常见场景是需要快速获取栈中的最小元素的问题,例如实现一个获取最小元素的栈(MinStack)或解决一些需要以常数时间获取最小值的算法问题。
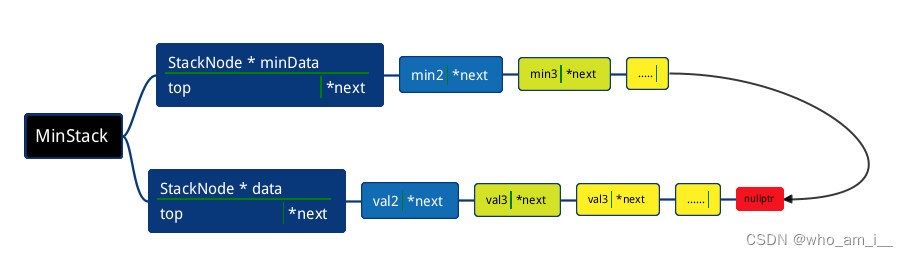
栈结构
代码实现
#include <iostream>
#ifndef TEST_MIN_STACK_H
#define TEST_MIN_STACK_H
using namespace std;
class StackNode{public:int val;StackNode * next;StackNode(int v):val(v),next(nullptr){}
};
class MinStack {
public:MinStack() {}void push(int val) {// 将元素压入栈StackNode* n;data == nullptr ? (data = new StackNode(val)) && nullptr : (n = new StackNode(val)) && (n->next = data) && (data = n);// 更新最小值栈if (minData == nullptr) {minData = new StackNode(val);}else if(val <= minData->val){StackNode* n = new StackNode(val);n->next = minData;minData = n;}}void pop() {if (data != nullptr) {// 取出栈顶元素int top = data->val;// 如果栈顶元素是最小值,同时从最小值栈中弹出if (minData != nullptr && top == minData->val) {StackNode* t = minData;minData = minData->next;delete t;}// 弹出栈顶元素StackNode* t = data;data = data->next;delete t;}}int top() {// if (data != nullptr) {// // 返回栈顶元素// return data->val;// }// // 当栈为空时,返回一个无意义的值// return INT_MIN;return data == nullptr ? INT_MIN : data->val;}int getMin() {//if (minData != nullptr) {// 返回最小值栈的栈顶元素// return minData->val;// }// 当栈为空时,返回一个无意义的值// return INT_MIN;return minData == nullptr ? INT_MIN : minData->val;}private:StackNode *data = nullptr;StackNode *minData = nullptr;
};#endif //TEST_MIN_STACK_H
实现分析
MinStack 类中有两个私有成员变量 data 和 minData,分别表示存储栈元素的栈和存储最小值的栈。这两个栈都是通过 StackNode 类的节点构成的。
下面是对 MinStack 类的各个方法进行分析:
-
void push(int val):将元素压入栈。该方法首先判断data是否为空,如果为空,则创建一个新的节点作为栈顶,并将data指向该节点;如果不为空,创建一个新节点并将其指向当前的栈顶节点,然后将data指向新的节点。接着,该方法更新最小值栈minData。如果minData为空,直接创建一个新节点作为最小值栈的栈顶;如果不为空,并且当前值小于等于最小值栈的栈顶元素,创建一个新节点,并将其指向最小值栈的栈顶节点,然后将minData指向新的节点。-
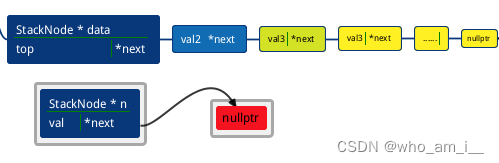
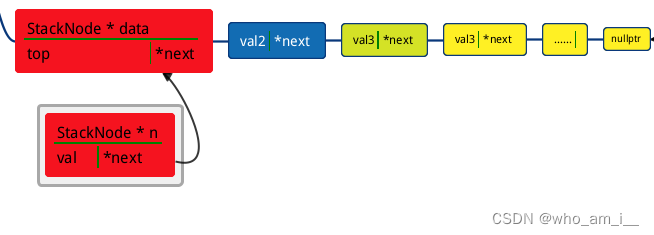
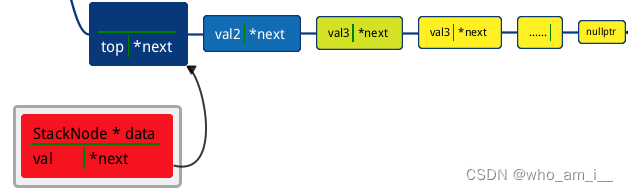
图解:
-
StackNode* n = new StackNode(val);
-
n->next = data;
-
data = n;
-
-
-
void pop():弹出栈顶元素。首先判断data是否为空,如果为空则直接返回。如果data不为空,则取出栈顶元素top。如果minData不为空且栈顶元素top等于最小值栈的栈顶元素,则将最小值栈的栈顶元素弹出。接着,将栈顶元素弹出,并释放内存。 -
int top():返回栈顶元素的值。如果data为空,返回INT_MIN,否则返回栈顶节点的值。 -
int getMin():返回最小值栈的栈顶元素的值。如果minData为空,返回INT_MIN,否则返回最小值栈的栈顶节点的值。
总体而言,该代码实现了一个基本的最小栈,支持在常数时间内进行入栈、出栈、获取栈顶元素和获取最小值的操作。
其他实现方式
使用stack,vector或deque实现MinStack。把其中的data和minData属性换成对应的容器对象即可。
相关文章:

C++ 数据结构之-最小栈(MinStack)
最小栈 最小栈(Min Stack)是一个支持常数时间复杂度获取栈中最小元素的特殊栈数据结构。通常,标准的栈数据结构只支持在常数时间内执行入栈(push)和出栈(pop)操作,但无法在常数时间内…...

【日常总结】优雅升级Swagger 2 升至 3.0, 全局设置 content-type application/json
目录 一、场景 二、问题 三、解决方案 四、延伸 上一节:【日常总结】Swagger-ui 导入 showdoc (优雅升级Swagger 2 升至 3.0)-CSDN博客 一、场景 接上一节:在 Swagger3Config extends WebMvcConfigurationSupport,…...
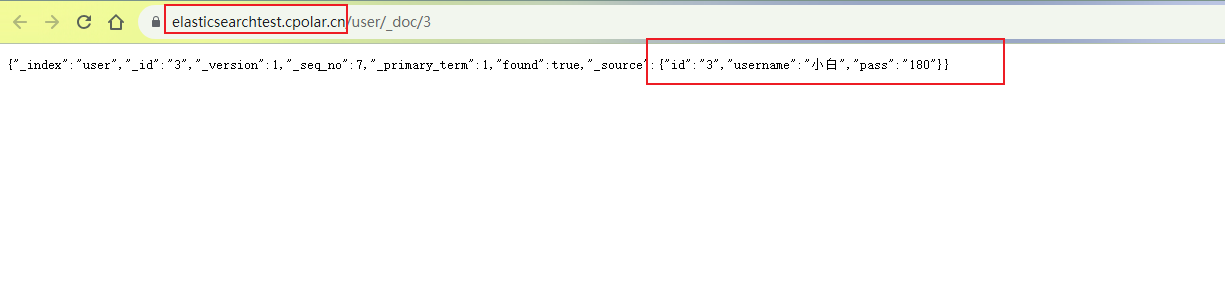
2023.11.27如何使用内网穿透工具实现Java远程连接操作本地Elasticsearch搜索引擎
文章目录 前言1. Windows 安装 Cpolar2. 创建Elasticsearch公网连接地址3. 远程连接Elasticsearch4. 设置固定二级子域名 前言 简单几步,结合Cpolar内网穿透工具实现Java远程连接操作本地Elasticsearch。 什么是elasticsearch?一个开源的分布式搜索引擎࿰…...

HNU 练习八 结构体编程题1. 评委打分
【问题描述】 校园卡拉OK比赛设置了7名评委,当一名选手K完歌之后,主持人报出歌手名字后,7位评委同时亮分,按照惯例,去掉一个最高分和一个最低分后,其余5位评委评分总和为该选手的最终得分。 一共有n组选手参…...
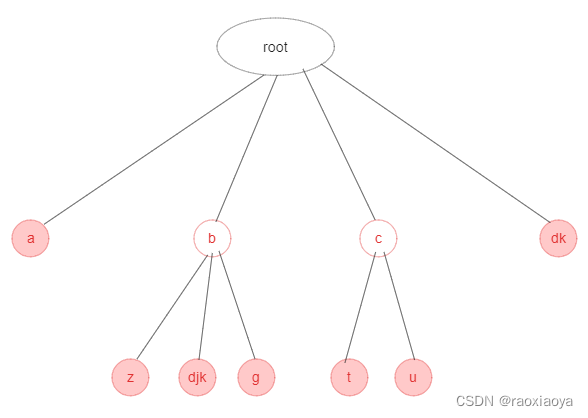
数据结构:字典树(前缀树,Trie树),压缩字典树(Radix)
字典树Trie Tree 字典树也称前缀树,Trie树。在 Elasticsearch 的倒排索引中用的也是 Trie 树。是一种针对字符串进行维护的数据结构。 字典树是对词典的一种存储方式,这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径,…...

前端学习系列之html
目录 初识html 发展史 优势 W3C 标准 地址 格式 网页基本标签 标题标签 段落标签 换行标签 水平线标签 字体样式 注释和特殊符号 特殊符号 图像、超链接 图像 常见图像格式 格式 超链接 格式 重要属性 href:规定链接指向的页面的 URL target…...
Star History 十月开源精选 |AI for Postgres
在 2023 年 Stack Overflow 开发者调查中,Postgres 顶替了 MySQL 被评为最受欢迎的数据库。一个重要因素应该是 Postgres 支持扩展:可扩展的架构 Postgres 仍然由社区拥有,Postgres 生态近年来蓬勃发展。 扩展可以看作是内置功能,…...
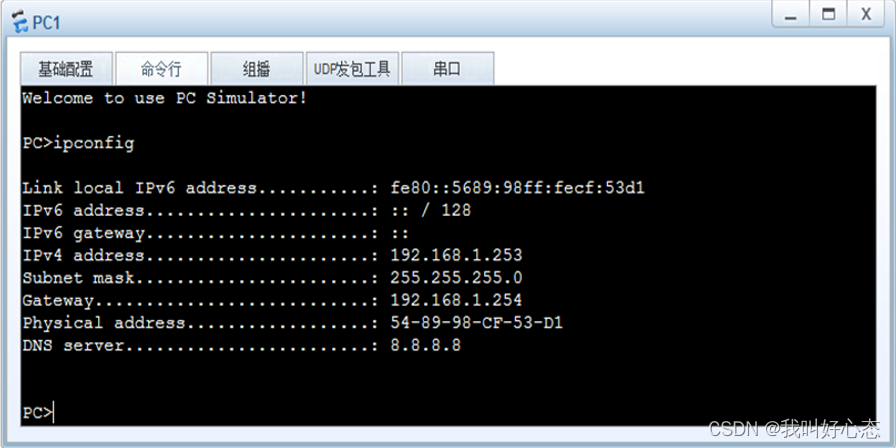
网络运维与网络安全 学习笔记2023.11.23
网络运维与网络安全 学习笔记 第二十四天 今日目标 VRRP负载均衡、BFD原理与配置、BFD典型应用 DHCP工作原理、全局模式DHCP VRRP负载均衡 VRRP单组缺陷 每网段存在一个VRRP组,缺点如下: 主网关数据转发压力大 备份网关不转发任何数据 网络设备利用…...
红黑树(万字图文详解)
红黑树 1. 红黑树的概念2. 红黑树的性质3. 红黑树节点的定义4. 红黑树结构5. 红黑树的插入操作5.1 按照二叉搜索的树规则插入新节点5.2 检测新节点插入后,红黑树的性质是否造到破坏5.2.1 情况一: cur为红,p为红,g为黑,u存在且为红…...
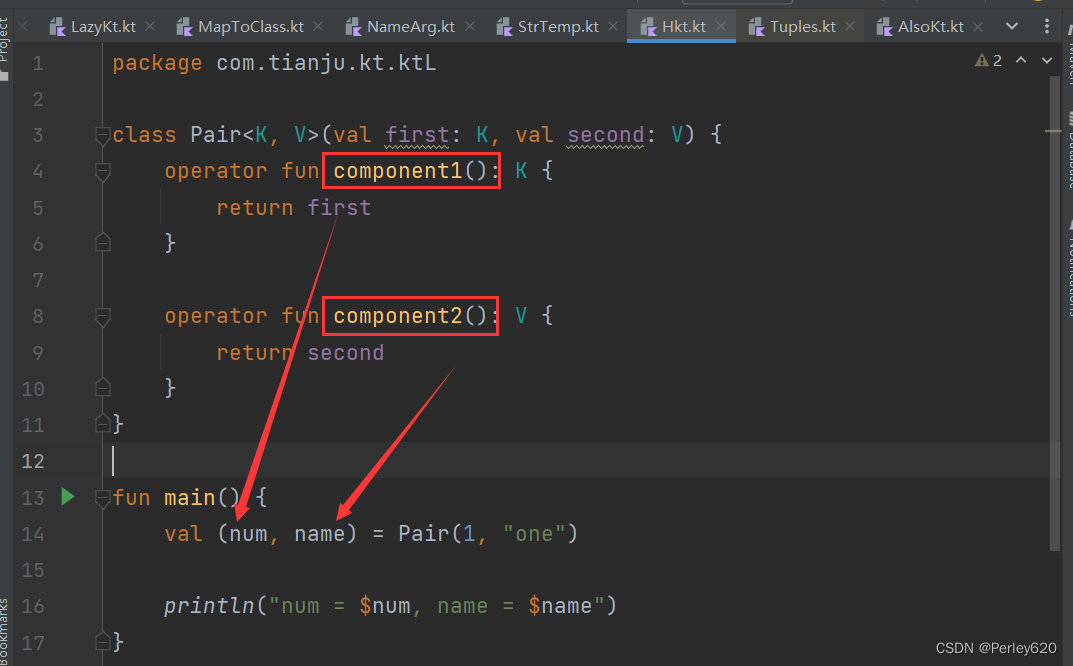
Kotlin学习——kt入门合集博客 kt里的委派模式Delegation kt里的特性
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...

数据挖掘 朴素贝叶斯
直入正题,直接看代码: 这是一段判断是不是藏话的代码 import numpy as np# 数据采集(定义函数加载数据集) def load_dataset():sent_list [[my, name, is, Devin],[you, are, stupid],[my, boyfriend, is, SB],[you, looks, ver…...

UI自动化测试工具有哪些优势?
UI自动化测试工具通过提高测试效率、覆盖率,减少测试时间和成本,以及支持持续集成等方式,为软件开发团队提供了一系列重要的优势,有助于提升软件质量和开发效率。 自动化执行:UI自动化测试工具可以模拟用户与应用程序的…...

【论文阅读笔记】InstructDiffusion: A Generalist Modeling Interface for Vision Tasks
【论文阅读笔记】StyleAvatar3D: Leveraging Image-Text Diffusion Models for High-Fidelity 3D Avatar Generation 论文阅读笔记论文信息引言动机挑战 方法结果 关键发现相关工作1. 视觉语言基础模型2. 视觉通用模型 方法/模型视觉任务的统一说明训练数据构建网络结构 实验设…...

笔记62:注意力汇聚 --- Nadaraya_Watson 核回归
本地笔记地址:D:\work_file\(4)DeepLearning_Learning\03_个人笔记\3.循环神经网络\第10章:动手学深度学习~注意力机制 a a a a a a a a a a a a a a a a...

给定一个n×n的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。
7-5 矩阵运算 分数 20 全屏浏览题目 切换布局 作者 C课程组 单位 浙江大学 给定一个nn的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。 输入格式: 输入第一行给出正整数n(…...

Go语言的学习笔记3——Go语言项目布局
Go 1.11 版本开始引入 go.mod 和 go.sum 以支持Go Module构建机制,而这种机制成为官方的依赖包管理方式。 现在Go可执行程序项目的典型布局如下所示: exe-layout ├── cmd/ │ ├── app1/ │ │ └── main.go │ └── app2/ │ └…...

70-76-堆、贪心算法
LeetCode 热题 100 文章目录 LeetCode 热题 100堆70. 中等-数组中的第K个最大元素71. 中等-前K个高频元素72. 困难-数据流中的中位数 贪心算法73. 简单-买卖股票的最佳时机74. 中等-跳跃游戏75. 中等-跳跃游戏II76. 中等-划分字母区间 本文存储我刷题的笔记。 堆 70. 中等-数组…...

Qt Network
Qt Network Qt Network为使用TCP/IP的应用程序编程提供了一组API。各种C++类处理诸如请求、cookies和通过HTTP发送数据之类的操作。 标题使用模块 使用Qt模块需要直接或通过其他依赖项链接到模块库。一些构建工具对此有专门的支持,包括CMake和qmake. 标题使用CMake构建 使…...
Win10电脑用U盘重装系统的步骤
在Win10电脑中,用户遇到了无法解决的系统问题,用户这时候就可以考虑重装Win10系统,这样即可轻松解决问题,从而满足自己的操作需求。接下来小编给大家详细介绍关于Win10电脑中用U盘重装系统的教程步骤。 准备工作 1. 一台正常联网可…...

安防视频监控/磁盘阵列/集中云存储平台EasyCVR设备录像保活不生效原因是什么?该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...