<JavaDS> 二叉树遍历各种遍历方式的代码实现 -- 前序、中序、后序、层序遍历
目录
有以下二叉树:
一、递归
1.1 前序遍历-递归
1.2 中序遍历-递归
1.3 后序遍历-递归
二、递归--使用链表
2.1 前序遍历-递归-返回链表
2.2 中序遍历-递归-返回链表
2.3 后序遍历-递归-返回链表
三、迭代--使用栈
3.1 前序遍历-迭代-使用栈
3.2 中序遍历-迭代-使用栈
3.3 后序遍历-迭代-使用栈
四、层序遍历
4.1 层序遍历-迭代-使用队列
4.2 层序遍历-迭代-返回二维链表
有以下二叉树:
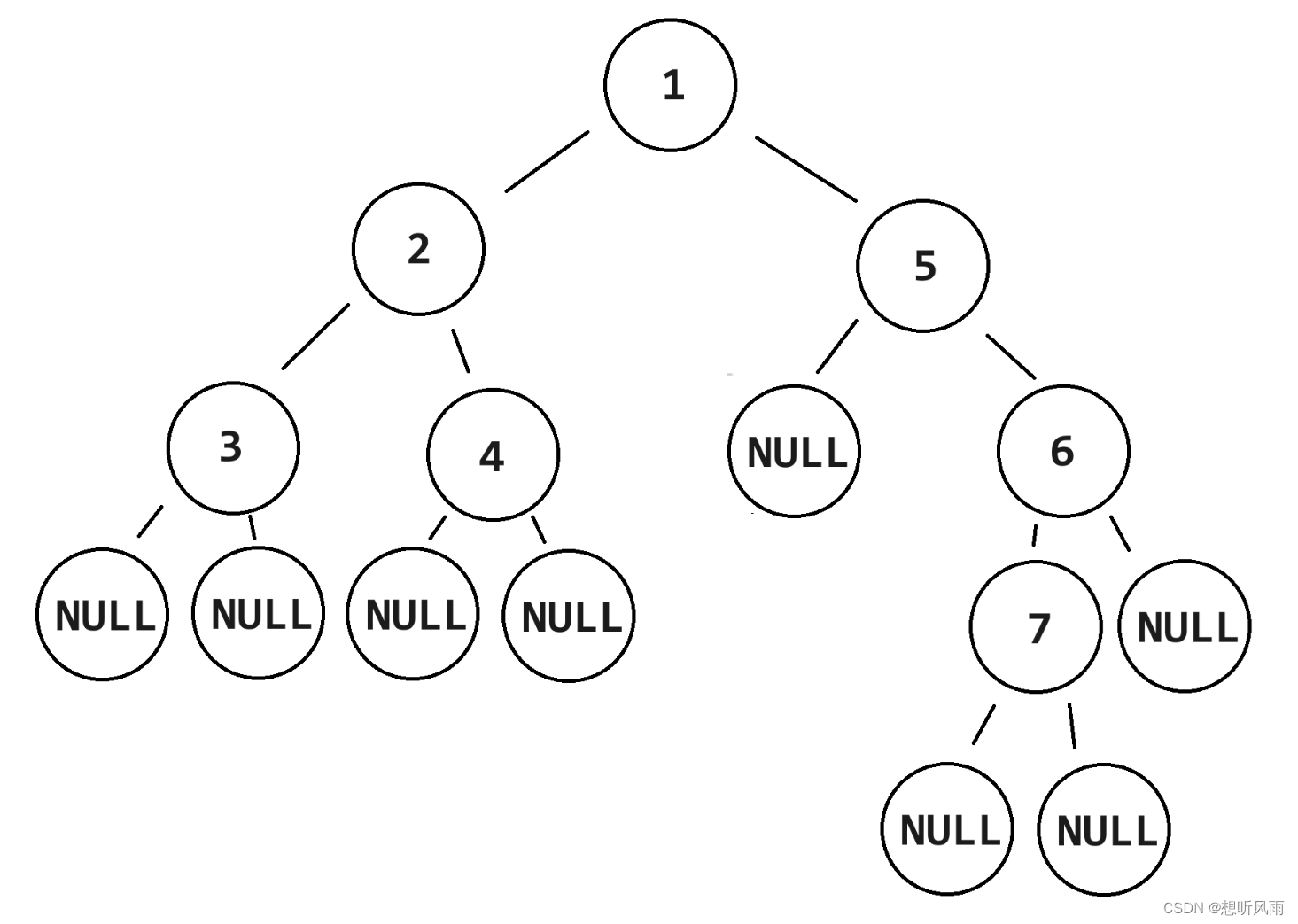
一、递归
| 逻辑/思路: | |
| 递归思想是将大问题分解为解法相似的小问题。 | |
| 已知根节点有左右子树,根节点的子节点又各有自己的左右子树,不断地对每棵子树进行左右分解,这就是从大问题到小问题。 | |
| 递归有两大关键条件:递推条件和回归条件,前者作用于递,后者作用于归。 | |
| 递推条件 | 在方法中,不断将左右子节点分别作为参数,重复调用本方法,每轮调用方法都在访问更深地子节点,达成了递归中的推进条件; |
| 回归条件 | 当访问到的节点为null时(如上图),就不能继续往下访问了,所以节点为null时,就return,这是回归条件; |
| 二叉树的前中后序递归遍历,思路基本相同,区别只在于调用方法和打印的顺序不同。 |
| 以下分别是二叉树的前序、中序、后序递归遍历的代码: |
1.1 前序遍历-递归
public static void PreorderTraversal1(TreeNode root) { //当前节点为null,则return;if(root == null){return;}//打印当前节点;System.out.print(root.val+" ");//找左子节点;PreorderTraversal1(root.left);//找右子节点;PreorderTraversal1(root.right);}//运行结果:
1 2 3 4 5 6 7 1.2 中序遍历-递归
public static void InorderTraversal1(TreeNode root) {//当前节点为null,则return;if(root == null){return;}//找左子节点;InorderTraversal1(root.left);//打印当前节点;System.out.print(root.val+" ");//找右子节点;InorderTraversal1(root.right);}//运行结果:
3 2 4 1 5 7 6 1.3 后序遍历-递归
public static void PostorderTraversal1(TreeNode root) {//当前节点为null,则return;if(root == null){return;}//找左子节点;PostorderTraversal1(root.left);//找右子节点;PostorderTraversal1(root.right);//打印当前节点;System.out.print(root.val+" ");}//运行结果:
3 4 2 7 6 5 1 二、递归--使用链表
| 逻辑/思路: | |
| 同样是使用递归的逻辑思想,只是由于使用了链表的数据结构,所以在递归的过程中需要将元素加入到链表中。 |
2.1 前序遍历-递归-返回链表
public static List<Integer> preorderTraversal2(TreeNode root){//新建链表;List<Integer> list = new ArrayList<>();//当前节点为null,则return;if(root == null){return list;}//add当前节点;list.add(root.val);//找当前节点的左子节点,并存储在新链表中;List<Integer> listLeft = preorderTraversal2(root.left);//将代表左子树的新链表中的元素全部添加到list中;list.addAll(listLeft);//找当前节点的右子节点,并存储在新链表中;List<Integer> listRight = preorderTraversal2(root.right);//将代表右子树的新链表中的元素全部添加到list中;list.addAll(listRight);//返回代表这个子树的list;return list;}//运行结果:
1 2 3 4 5 6 7 2.2 中序遍历-递归-返回链表
public static List<Integer> InorderTraversal2(TreeNode root){//新建链表;List<Integer> list = new ArrayList<>();//当前节点为null,则return;if(root == null){return list;}//找当前节点的左子节点,并存储在新链表中;List<Integer> listLeft = InorderTraversal2(root.left);//将代表左子树的新链表中的元素全部添加到list中;list.addAll(listLeft);//add当前节点;list.add(root.val);//找当前节点的右子节点,并存储在新链表中;List<Integer> listRight = InorderTraversal2(root.right);//将代表右子树的新链表中的元素全部添加到list中;list.addAll(listRight);//返回代表这个子树的list;return list;}//运行结果:
3 2 4 1 5 7 6 2.3 后序遍历-递归-返回链表
public static List<Integer> PostorderTraversal2(TreeNode root){//新建链表;List<Integer> list = new ArrayList<>();//当前节点为null,则return;if(root == null){return list;}//找当前节点的左子节点,并存储在新链表中;List<Integer> listLeft = PostorderTraversal2(root.left);//将代表左子树的新链表中的元素全部添加到list中;list.addAll(listLeft);//找当前节点的右子节点,并存储在新链表中;List<Integer> listRight = PostorderTraversal2(root.right);//将代表右子树的新链表中的元素全部添加到list中;list.addAll(listRight);//add当前节点;list.add(root.val);//返回代表这个子树的list;return list;}//运行结果:
3 4 2 7 6 5 1 三、迭代--使用栈
| 逻辑/思路: | |
| 迭代是使用栈来帮助遍历二叉树。这种遍历方式利用了栈“后进先出”的特点,来达到对二叉树中的父节点进行回溯的目的。 也就是说,当遍历到一个节点即将该节点压栈,当完成对左子树的访问之后,利用弹出并记录栈顶元素的方式,得到左子树的父节点,并通过这个父节点访问右子树。 因为压栈的第一个元素必然为根节点,因此,当栈为空时,必然全部节点都遍历完成了。 |
3.1 前序遍历-迭代-使用栈
public static void PreorderTraversal3(TreeNode root){//如果root为null,return;if(root == null){return;}//新建一个栈;Stack<TreeNode> stack = new Stack<>();//将根节点压栈;stack.push(root);//如果栈不为空;while (!stack.isEmpty()){//弹出栈顶元素,并记录为cur;TreeNode cur = stack.pop();//因为是前序遍历,打印当前节点,再进行后续操作;System.out.print(cur.val+" ");//如果cur的右子节点不为空,则将其压栈;if(cur.right != null){stack.push(cur.right);}//如果cur的左子节点不为空,则将其压栈;if(cur.left != null){stack.push(cur.left);}}}//运行结果:
1 2 3 4 5 6 7 | 为什么压栈先压右子节点,再压左子节点? |
| 因为要按前序遍历打印,而栈是后进先出,所以后压左子节点,等下先弹出的也是左子节点,先弹出先打印。 |
3.2 中序遍历-迭代-使用栈
public static void InorderTraversal3(TreeNode root){//如果root为null,return;if(root == null){return;}//新建一个栈;Stack<TreeNode> stack = new Stack<>();//用一个临时“指针”记录root(因为要移动指针,不然等下根节点跑哪去都不知道了)TreeNode cur = root;//如果cur不为空或者栈不为空;while (cur != null || !stack.isEmpty()){//如果节点不为空,则将节点压栈,并让指针不断向左子节点移动,直到节点为空;//当循环停下时,此时栈顶元素必然是树中最左边且未被遍历过的节点;while (cur != null){stack.push(cur);cur = cur.left;}//弹出栈顶元素,并记录为pre;TreeNode pre = stack.pop();//因为是中序遍历,打印当前节点,再进行后续操作;System.out.print(pre.val+" ");//如果pre的右子节点不为空,则将指针cur移动到右子节点上;if(pre.right != null){cur = pre.right;}}}//运行结果:
3 2 4 1 5 7 6 | 为什么进入循环的判断条件是cur != null || !stack.isEmpty()? |
| cur不为空的判断条件是为了让一开始栈中还没有元素时,能够顺利进入循环。 栈不为空代表还有元素没有遍历。 |
3.3 后序遍历-迭代-使用栈
public static void PostorderTraversal3(TreeNode root){//如果root为null,return;if(root == null){return;}//新建一个栈;Stack<TreeNode> stack = new Stack<>();//用一个临时“指针”记录root(因为要移动指针,不然等下根节点跑哪去都不知道了)TreeNode cur = root;//将根节点压栈;stack.push(root);//如果栈不为空;while (!stack.isEmpty()) {//查看并记录栈顶元素这个节点;TreeNode peek = stack.peek();//根据以下条件,进行后续操作;if (peek.left != null && peek.left != cur && peek.right != cur) {stack.push(peek.left);} else if (peek.right != null && peek.right != cur) {stack.push(peek.right);} else {System.out.print(stack.pop().val + " ");cur = peek;}}}//运行结果:
3 4 2 7 6 5 1 | 上述代码中的 if...else if..else 为什么这样设置条件? | |
| if (peek.left != null && peek.left != cur && peek.right != cur) { stack.push(peek.left); } | |
| 判断peek有没有左子节点,且peek的左右子节点有没有被处理过; | |
| 如果左右子节点都没有被处理过,那么将peek的左子节点压栈; | |
| else if (peek.right != null && peek.right != cur) { stack.push(peek.right); } | |
| 再判断peek有没有右子节点,且peek的右子节点有没有被处理过; | |
| 在这里不能对左子节点判断是否操作过,因为是先遍历的左子节点,如果存在左子节点必然是操作过的。所以如果加入左子节点的判断,则必然进不了这个else if; | |
| 如果右子节点没有被处理过,那么将peek的右子节点压栈; | |
| 通过前两个条件可以看出,只要有左子节点,必然先处理左子节点,没有左子节点或者左子节点被处理完了,才开始处理右子节点;处理方法如下: | |
| else { System.out.print(stack.pop().val + " "); cur = peek; } | |
| 直到所有左右子节点处理完毕,最后一个弹出栈并被处理的,必然是一开始压栈的根节点root。 | |
四、层序遍历
| 逻辑/思路: | |
| 层序遍历与前序、中序、后序遍历都不同,层序遍历使用的是队列的数据结构进行遍历。 核心思想是利用队列“先进先出”和“队头出,队尾入”的特点,分层遍历二叉树。 如果需要返回一个二维链表,则是将二叉树每层的节点按顺序添加到各个链表中,每个链表代表一层,最终链表将作为元素,被添加到二维链表中; |
4.1 层序遍历-迭代-使用队列
public static void SequenceTraversal1(TreeNode root){//如果root为null,return;if(root == null){return;}//创建队列,root入队列;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);//如果队列中还有元素;while (queue.size() != 0){//队首出队列并记录cur;TreeNode cur = queue.poll();//打印cur的值;System.out.print(cur.val + " ");//如果cur有左子节点,将左子节点入队列;if(cur.left != null){queue.offer(cur.left);}//如果cur有右子节点,将右子节点入队列;if(cur.right != null){queue.offer(cur.right);}}}//运行结果:
1 2 5 3 4 6 7 4.2 层序遍历-迭代-返回二维链表
public static List<List<Integer>> SequenceTraversal2(TreeNode root){//创建二维链表diList;List<List<Integer>> diList = new LinkedList<>();//如果root为空则return;if(root == null){return diList;}//创建队列,root入队列;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);//如果队列中还有元素;while(!queue.isEmpty()){//计算队列中的元素数量;int size = queue.size();//创建链表,用于存储每层的节点;List<Integer> list = new LinkedList<>();//根据上面的size确定需要循环多少次,即处理多少个节点;while (size>0){//队首出队列;TreeNode cur = queue.poll();//出队列一个size就--;size--;//把出队列的元素添加到list中;list.add(cur.val);//如果cur有左子节点,将左子节点入队列;if(cur.left != null){queue.offer(cur.left);}//如果cur有右子节点,将右子节点入队列;if(cur.right != null){queue.offer(cur.right);}}//把链表list添加到diList中;diList.add(list);}//返回diList;return diList;}//运行结果:
1 2 5 3 4 6 7 相关文章:

<JavaDS> 二叉树遍历各种遍历方式的代码实现 -- 前序、中序、后序、层序遍历
目录 有以下二叉树: 一、递归 1.1 前序遍历-递归 1.2 中序遍历-递归 1.3 后序遍历-递归 二、递归--使用链表 2.1 前序遍历-递归-返回链表 2.2 中序遍历-递归-返回链表 2.3 后序遍历-递归-返回链表 三、迭代--使用栈 3.1 前序遍历-迭代-使用栈 3.2 中序遍…...
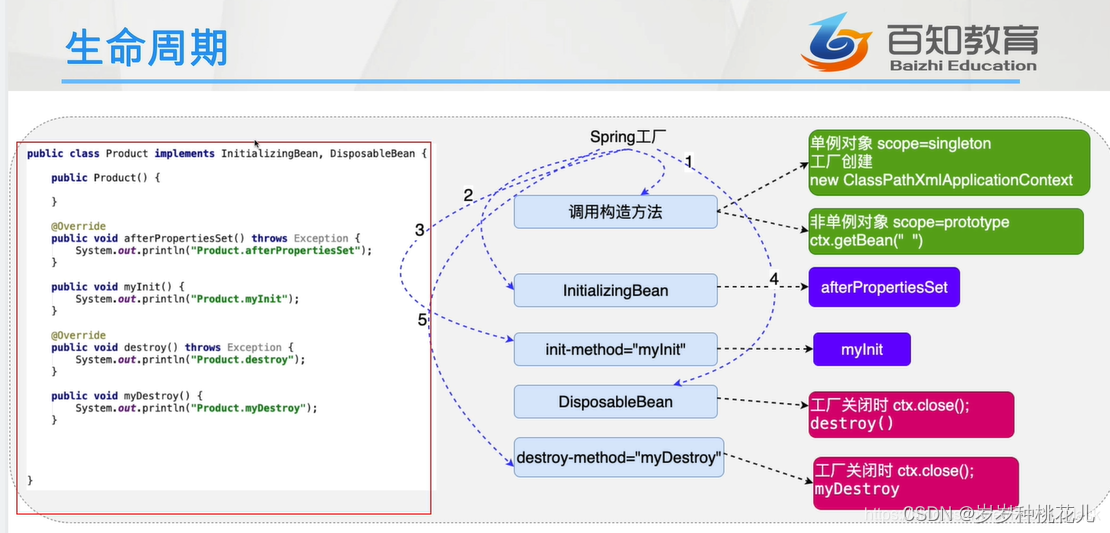
如何控制Spring工厂创建对象的次数?详解Spring对象的声明周期!
😉😉 学习交流群: ✅✅1:这是孙哥suns给大家的福利! ✨✨2:我们免费分享Netty、Dubbo、k8s、Mybatis、Spring...应用和源码级别的视频资料 🥭🥭3:QQ群:583783…...
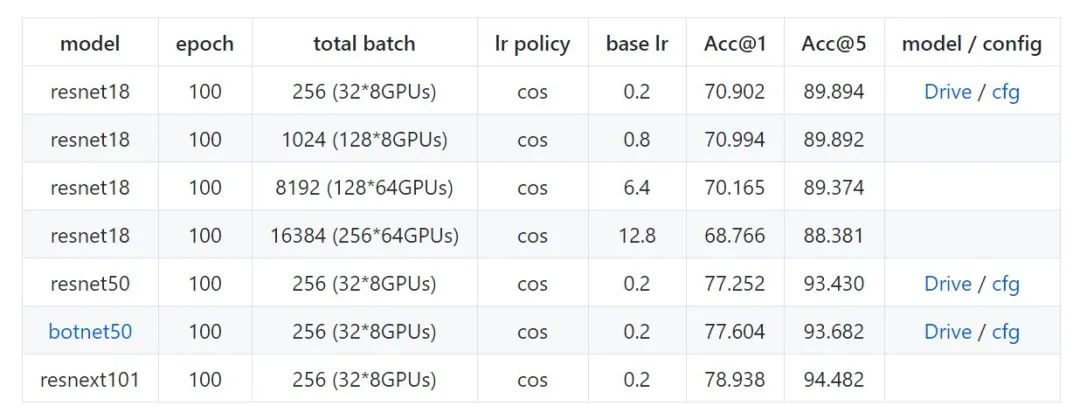
计算机杂谈系列精讲100篇-【计算机应用】PyTorch部署及分布式训练
目录 C平台PyTorch模型部署流程 1.模型转换 1. 不支持的操作 2. 指定数据类型 2.保存序列化模型 3.C load训练好的模型 4. 执行Script Module PyTorch分布式训练 分布式并行训练概述 Pytorch分布式数据并行 手把手渐进式实战 A. 单机单卡 B. 单机多卡DP C. 多机多卡DDP D. L…...

Opencv-C++笔记 (19) : 分水岭图像分割
文章目录 一、基于距离变换与分水岭的图像分割1、图像分割2、距离和变换与分水岭距离变换常见算法有两种分水岭变换常见的算法 3、距离变换API函数接口4、watershed 分水岭函数API接口步骤 5、代码 一、基于距离变换与分水岭的图像分割 1、图像分割 图像分割(Image Segmentat…...

Linux以nohup方式运行jar包
1、在需要运行的jar包同级目录下建立启动脚本文件: 文件内容: #! /bin/bash #注意:必须有&让其后台执行,否则没有pid生成 jar包路径为绝对路径 nohup java -jar /usr/local/testDemo/jdkDemo-0.0.1-SNAPSHOT.jar >/us…...
【c++|SDL】开始使用之---demo
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 SDL 记录 1. hello word #include<SDL2/SDL.h>SDL_Window* g_pWindow 0; SDL_Renderer* g_pRenderer 0;int main(int argc, char* args[]) {//…...
leetcode:有效的括号
题目描述 题目链接:20. 有效的括号 - 力扣(LeetCode) 题目分析 题目给了我们三种括号:()、{ }、[ ] 这里的匹配包括:顺序匹配和数量匹配 最优的思路就是用栈来解决: 括号依次入栈…...

使用STM32微控制器实现光电传感器的接口和数据处理
光电传感器在许多领域中被广泛应用,例如工业自动化、智能家居等。本文将介绍如何使用STM32微控制器实现光电传感器的接口和数据处理的方案,包括硬件设计、引脚配置、数据采集、滤波和阈值判断等关键步骤,并给出相应的代码示例。 一、引言 光…...
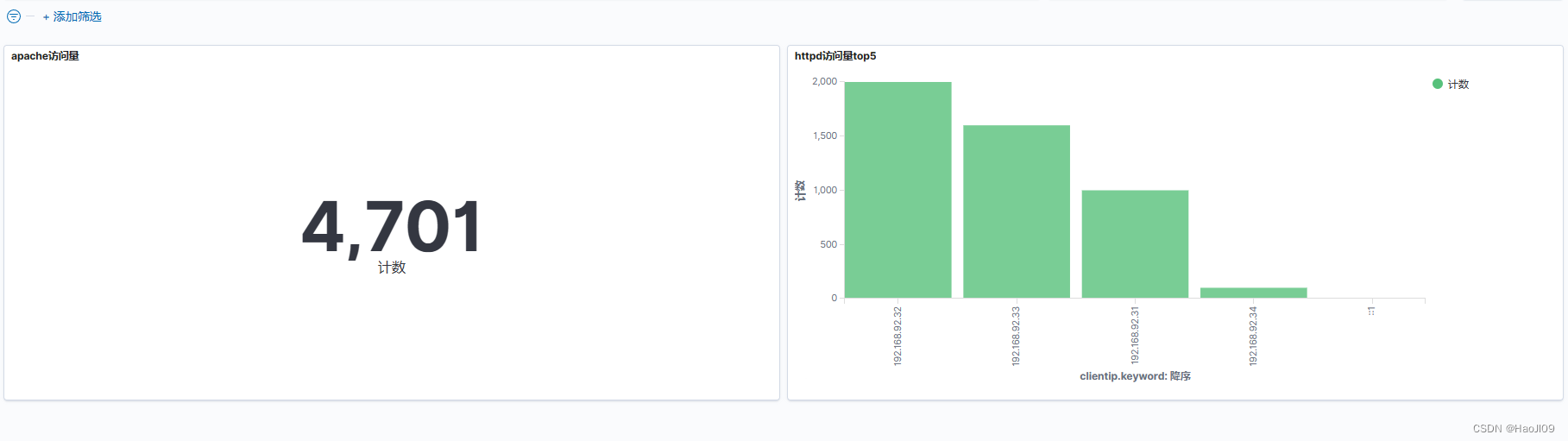
ELK企业级日志分析平台——kibana数据可视化
部署 新建虚拟机server5,部署kibana [rootelk5 ~]# rpm -ivh kibana-7.6.1-x86_64.rpm [rootelk5 ~]# cd /etc/kibana/[rootelk5 kibana]# vim kibana.ymlserver.host: "0.0.0.0"elasticsearch.hosts: ["http://192.168.56.11:9200"]i18n.local…...
Shell条件变量练习
1.算数运算命令有哪几种? (1) "(( ))"用于整数运算的常用运算符,效率很高 [rootshell scripts]# echo $((24*5**2/8)) #(( ))2452814 14 (2) "$[ ] "用于整数运算 [rootshell scripts]# echo $[24*5**2/8] #[ ]也可以运…...

【PHP】MySQL简介与MySQLi函数(含PHP与MySQL交互)
文章目录 一、MySQL简介二、MySQLi函数1. 开启mysqli扩展:2. PHP MySQLi扩展的常用函数 三、PHP与MySQL交互0. 准备1. 创建连接(mysqli_connect() )连接mysql语法 2. 选择数据库(mysqli_select_db())3. 在php中操作数据…...

vscode在Windows上安装插件提示错误xhr failed
问题描述: 在Windows下,在vscode里搜索扩展时发现无法搜索,报如下错:”Error while fetching extensions. XHR failed“。 问题定位: 在vscode界面下键入ctrlshiftp, 然后输入:Developer: T…...
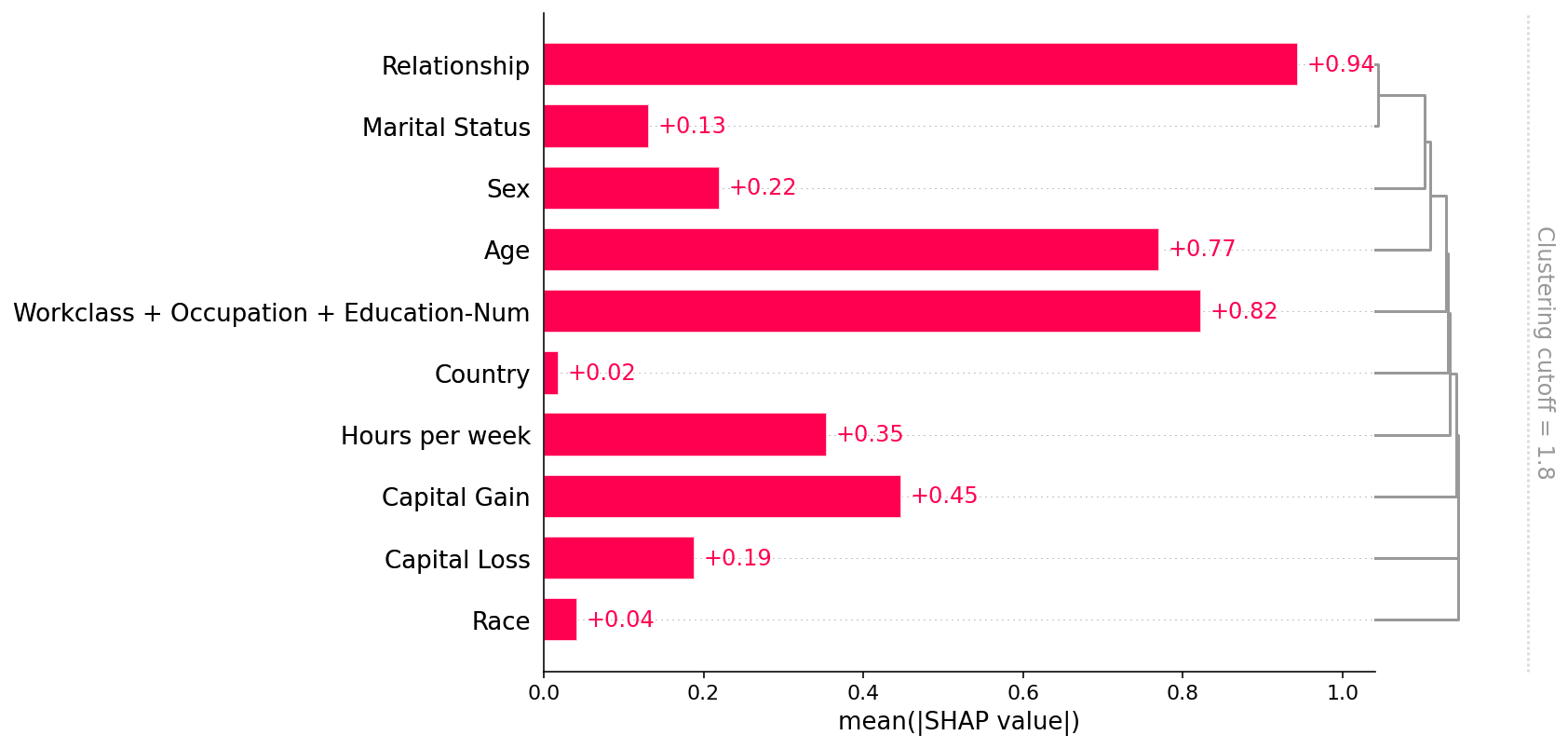
SHAP(一):具有 Shapley 值的可解释 AI 简介
SHAP(一):具有 Shapley 值的可解释 AI 简介 这是用 Shapley 值解释机器学习模型的介绍。 沙普利值是合作博弈论中广泛使用的方法,具有理想的特性。 本教程旨在帮助您深入了解如何计算和解释基于 Shapley 的机器学习模型解释。 我…...
C++数据结构:图
目录 一. 图的基本概念 二. 图的存储结构 2.1 邻接矩阵 2.2 邻接表 三. 图的遍历 3.1 广度优先遍历 3.2 深度优先遍历 四. 最小生成树 4.1 最小生成树获取策略 4.2 Kruskal算法 4.3 Prim算法 五. 最短路径问题 5.1 Dijkstra算法 5.2 Bellman-Ford算法 5.3 Floyd-…...

「C++」红黑树的插入(手撕红黑树系列)
💻文章目录 📄前言红黑树概念红黑树的结构红黑树节点的定义红黑树的定义红黑树的调整 红黑树的迭代器迭代器的声明operator( )opeartor--( ) 完整代码 📓总结 📄前言 作为一名程序员相信你一定有所听闻红黑树的大名,像…...

2023年生肖在不同时间段的运势预测
随着信息技术的飞速发展,API已经成为了数据获取和交互的重要途径。很多网站和APP都在运用API来获取数据。今天我们来介绍一个十分有趣的API——《十二生肖运势预测API》,通过这个API,我们可以获取到每个生肖在不同时间段的运势预测࿰…...
ERRO报错
无法下载nginx 如下解决: 查看是否有epel 源 安装epel源 安装第三方 yum -y install epel-release.noarch NGINX端口被占用 解决: 编译安装的NGINX配置文件在/usr/local/ngin/conf 修改端口...

shiyan
import javax.xml.transform.Result; import java.util.Arrays; public class ParseText {//需要统计的字符串为private String text"Abstract-This paper presents an overview";private Result[] res;private int count;public ParseText(){resnew Result[100];cou…...
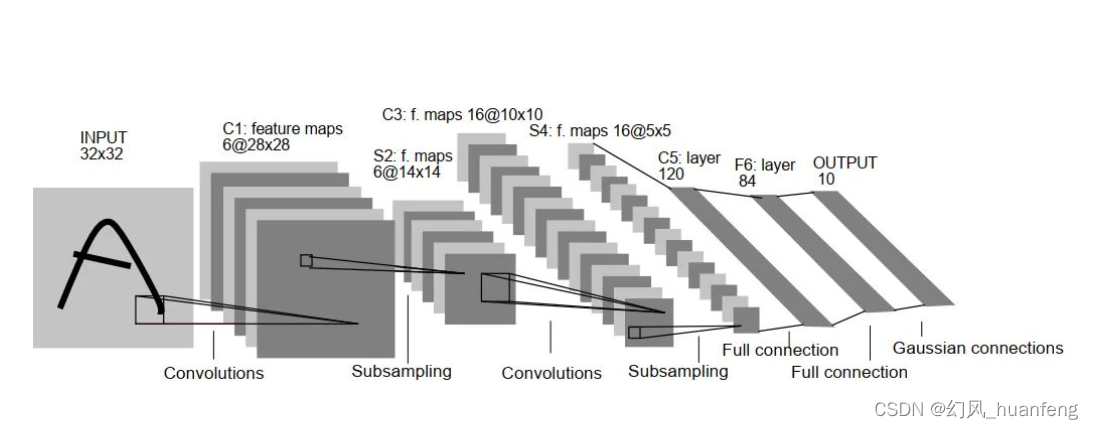
深度学习黎明时期的LeNet:揭开卷积神经网络的序幕
在深度学习的历史长河中,Yann LeCun 的 LeNet 是一个里程碑式的研究成果,它为后来的卷积神经网络(Convolutional Neural Networks,CNN)的发展奠定了基础。LeNet 的诞生标志着深度学习黎明时期的到来,为人工…...
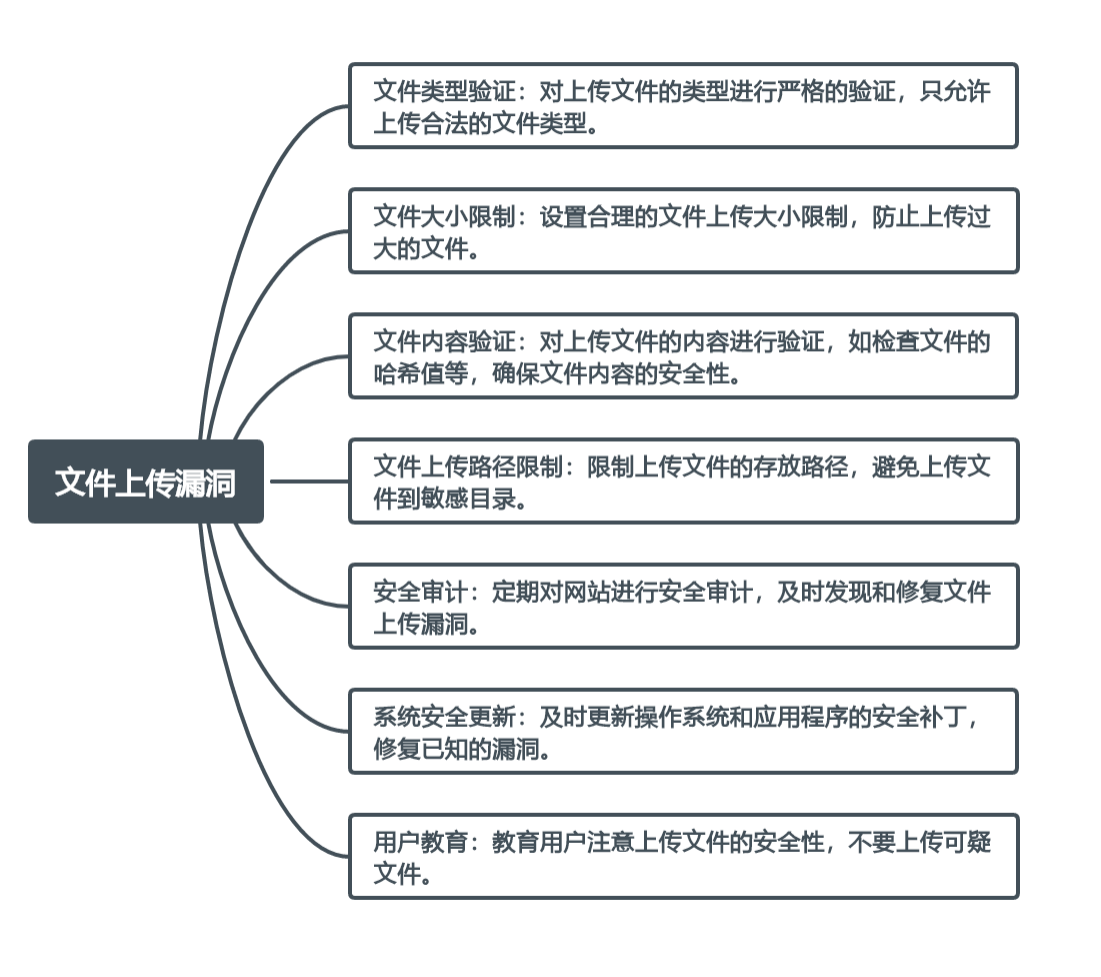
跨越威胁的传说:揭秘Web安全的七大恶魔
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
