报错解决:You may need an additional loader to handle the result of these loaders.
报错信息如下
- vue 项目
Module parse failed: Unexpected token (1:9)
File was processed with these loaders:* ./node_modules/@vue/cli-plugin-babel/node_modules/cache-loader/dist/cjs.js* ./node_modules/babel-loader/lib/index.js* ./node_modules/eslint-loader/index.js
You may need an additional loader to handle the result of these loaders.
> export * as homeApi from './modules/homeDataPanel';
| export * as loginApi from './modules/login';
| export * as collegApi from './modules/basicWork/collegeManger';
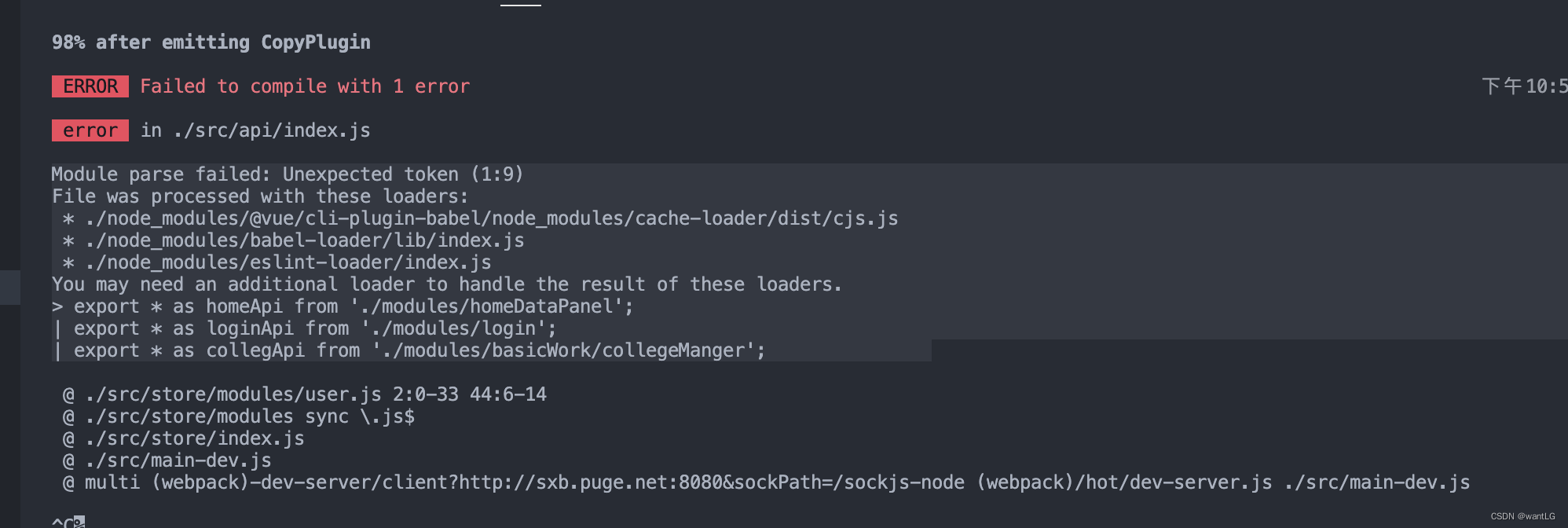
根因是:当前webpack/babel 识别不了 export * as x x x from xxxx的语法(export 和 import的组合使用)
解决
npm i @babel/preset-env @babel/plugin-transform-modules-commonjs -D
- 在babel.config.js中配置
module.exports = {presets: ['@babel/preset-env',...],plugins: ['@babel/plugin-transform-modules-commonjs',....]
};或者 在.babelrc中配置
{ "presets": ["@babel/preset-env"], "plugins": ["@babel/plugin-transform-modules-commonjs"]
}
相关文章:

报错解决:You may need an additional loader to handle the result of these loaders.
报错信息如下 vue 项目 Module parse failed: Unexpected token (1:9) File was processed with these loaders:* ./node_modules/vue/cli-plugin-babel/node_modules/cache-loader/dist/cjs.js* ./node_modules/babel-loader/lib/index.js* ./node_modules/eslint-loader/in…...
配置自动化部署Jenkins和Gitea
配置自动化部署 这里使用的是JenkinsGitea 如果不知道怎么安装Jenkins和Gitea可以参考下面文章 https://blog.csdn.net/weixin_46533577/article/details/134644144 我的另一篇文章 介绍 前端 先说下自己的情况,因为自己服务器原因,使用的服务器内…...

VSCODE+QEMU+WSL调试RISCV代码(SBI、kernel)
前言 最近在对RISC-V架构比较感兴趣,正好手头有《RISC-V体系结构编程与实践》的书籍,就打算跟随笨叔将这块的知识学习起来,最开始当然是需要搭建一个基础的实验平台,本来笨叔是贴心的提供了VMare的环境,奈何天生叛逆的…...
二叉树(判断是否为对称二叉树)
题目(力扣): 观察题目,只需判断该二叉树是否对称。 判断二叉树是否对称,就可以换位去判断该二叉树的左子树和右子树是否对称。 这时就可以写一个辅助函数来方便判断。 该函数是判断两颗树是否镜像对称,这…...

STM32开发学习(地址映射)
LED灯代码: #define PERIPH_BASE ((unsigned int)0x40000000)#define AHB1PERIPH_BASE (PERIPH_BASE 0x00020000)#define GPIOF_BASE (AHB1PERIPH_BASE 0x1400)#define GPIOF_MODER *(unsigned int*)(GPIOF_BASE0x00) #define GPIOF_BSRR *(uns…...
 =E(X) + E(Y))
证明E(X+Y) =E(X) + E(Y)
E(XY) E(X) E(Y)的成立是不需要X和Y相互独立的!!! 离散型随机变量 E ( X Y ) ∑ i 1 n ∑ j 1 m ( x i y j ) P { X x i , Y y j } ∑ i 1 n ∑ j 1 m x i P { X x i , Y y j } ∑ i 1 n ∑ j 1 m y j P { X x i , Y y j …...

ClickHouse入门手册1.0
1、数据类型 1.1 整数类型: ClickHouse中整型数据均为固定长度(可以设置长度参数,但是会被忽略),整型包括有符号整型和无符号整型。 有符号整型:Int8,Int16,Int32,Int64,Int128,Int256 无符号整型:UInt8,UInt16,UI…...
10个火爆的设计素材网站推荐
所谓聪明的女人没有米饭很难做饭,设计师也是如此。如何找到优秀的设计材料是每个设计师的痛点,国内材料网站收费,但也限制使用范围和期限,大多数外国设计网站不能打开或需要特殊互联网使用,有一定的安全风险。 作为一…...
SQL注入 - CTF常见题型
文章目录 题型一 ( 字符型注入 )题型二 ( 整数型注入 )题型三 ( 信息收集SQL注入)题型四 ( 万能密码登录 )题型五 ( 搜索型注入文件读写 )题型六 (…...
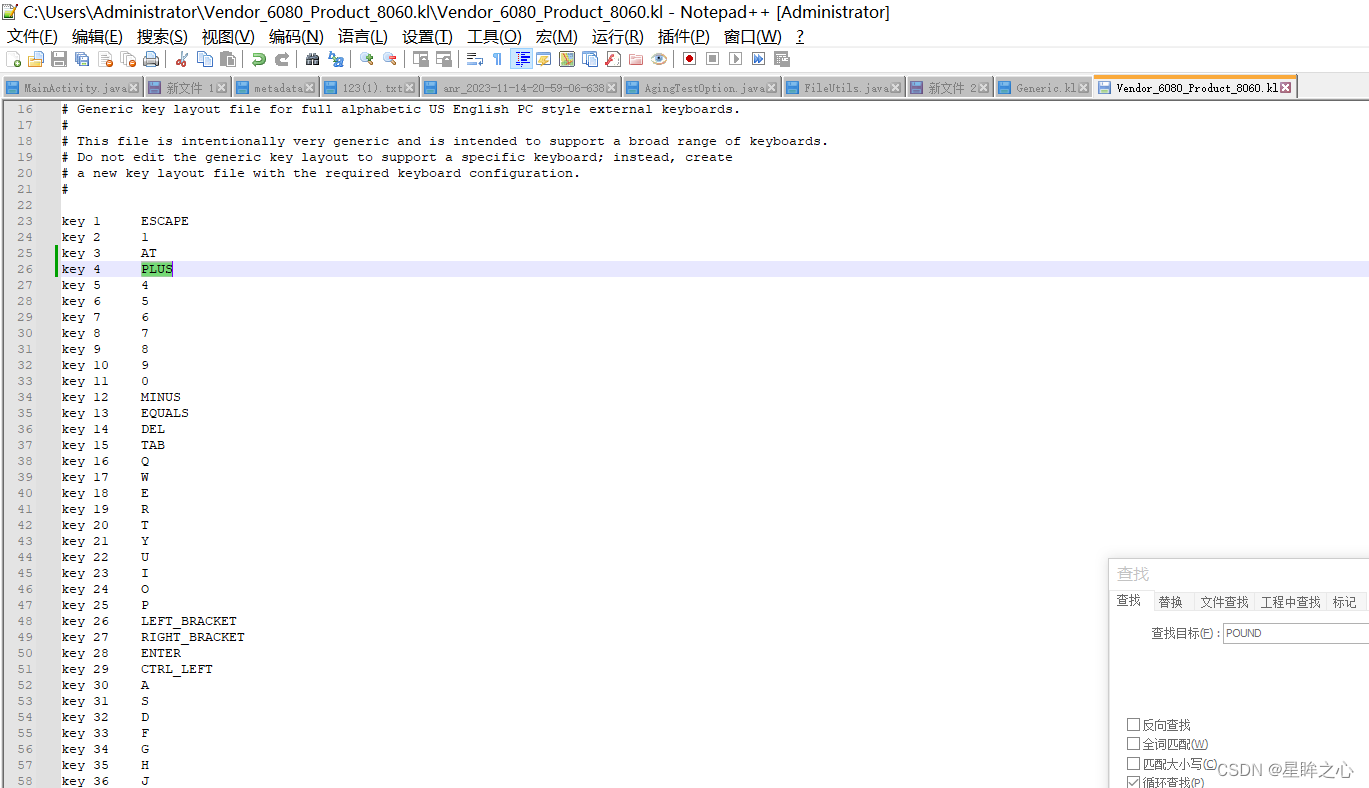
android keylayout键值适配
1、通过getevent打印查看当前keyevent数字对应事件和物理码 2、dumpsys input 查看输入事件对应的 KeyLayoutFile: /system/usr/keylayout/Vendor_6080_Product_8060.kl 3、通过物理码修改键值映射,修改/system/usr/keylayout/目录下的文件...

python读取excel自动化生成sql建表语句和java实体类字段
1、首先准备一个excel文件: idtypenameidint学号namestring姓名ageint年龄sexstring性别weightdecimal(20,4)体重scoredecimal(20,4)分数 2、直接生成java字段和注释: import pandas as pddf pd.read_excel(test.xlsx, sheet_nameSheet1)for i in ran…...
Unity求向量A在平面L上的投影向量
如题:求向量A在平面L上的投影向量(图左) 即求 其实等价于求向量,那在中,,所以只需要求即可 而就是在平面L的法向量的投影坐标,所以代码就是 /// <summary>/// 求向量A在平面B上的投影向量/// </summary>/// <para…...

人机交互2——任务型多轮对话的控制和生成
1.自然语言理解模块 2.对话管理模块 3.自然语言生成模块...

【数据结构】八大排序 (三)
目录 前言: 快速排序 快速排序非递归实现 快速排序特性总结 归并排序 归并排序的代码实现 归并排序的特性总结 计数排序 计数排序的代码实现 计数排序的特性总结 前言: 前文快速排序采用了递归实现,而递归会开辟函数栈帧࿰…...
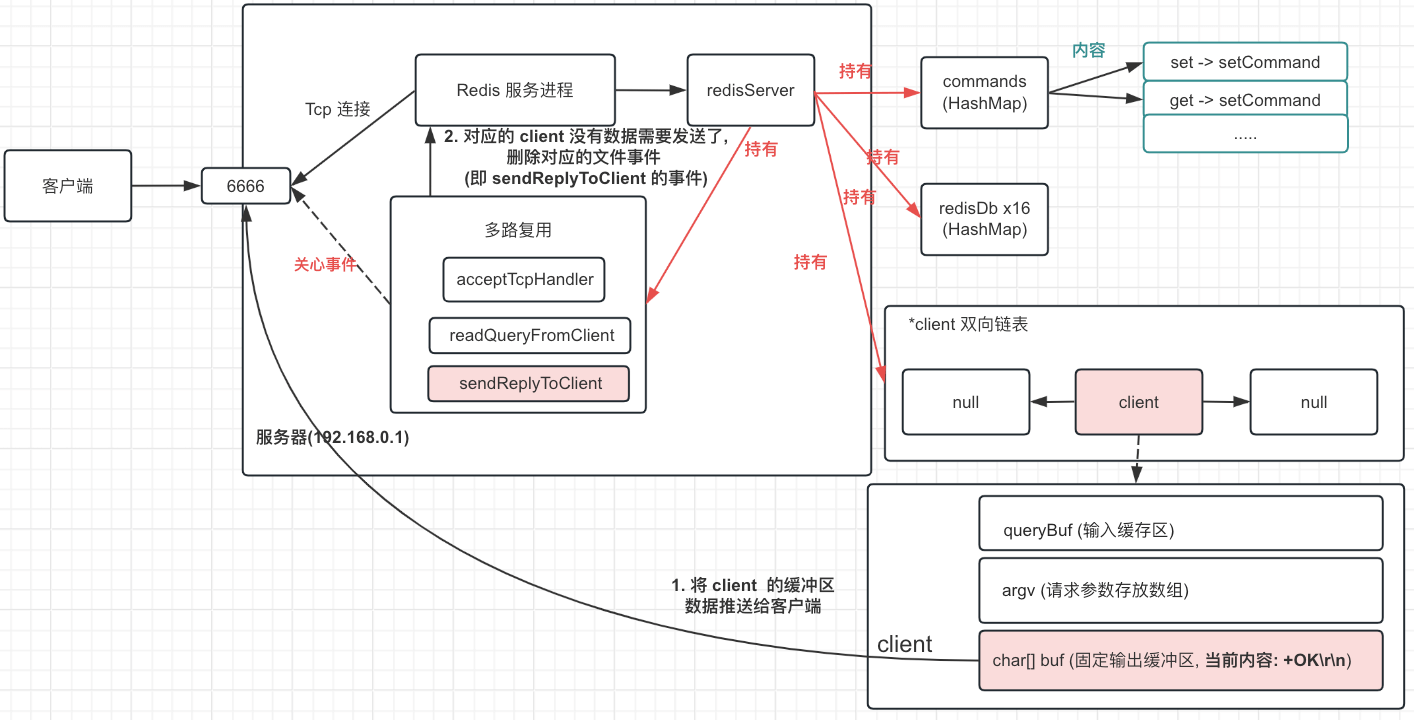
Redis 命令处理过程
我们知道 Redis 是一个基于内存的高性能键值数据库, 它支持多种数据结构, 提供了丰富的命令, 可以用来实现缓存、消息队列、分布式锁等功能。 而在享受 Redis 带来的种种好处时, 是否曾好奇过 Redis 是如何处理我们发往它的命令的呢? 本文将以伪代码的形式简单分析…...

python爬虫进阶教程之如何正确的使用cookie
文章目录 前言一、获取cookie二、程序实现三、动态获取cookie四、其他关于Python爬虫技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③Python小游戏源码五、面试资料六、Pytho…...

【hacker送书第4期】推荐4本Java必读书籍(各送一本)
第4期图书推荐 Java从入门到精通(第7版)内容简介参与方式 项目驱动零基础学Java内容简介参与方式 深入理解Java高并发编程内容简介参与方式 Java编程讲义内容简介参与方式 Java从入门到精通(第7版) 内容简介 《Java从入门到精通&…...

[密码学]DES
先声明两个基本概念 代换(substitution),用别的元素代替当前元素。des的s-box遵循这一设计。 abc-->def 置换(permutation),只改变元素的排列顺序。des的p-box遵循这一设计。 abc-->bac DES最核心的算法就是…...

15个超级实用的Python操作,肯定有你意想不到的!
文章目录 1)映射代理(不可变字典)2)dict 对于类和对象是不同的3) any() 和 all()4) divmod()5) 使用格式化字符串轻松检查变量6) 我们可以将浮点数转换为比率7) 用globals()和locals()显示现有的全局/本地变量8) import() 函数9) …...

GitHub上8个强烈推荐的 Python 项目
文章目录 前言1. Manim2. DeepFaceLab3. Airflow4. GPT-25. XSStrike6. 谷歌图片下载7. Gensim8. SocialMapper总结关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
