二叉树(判断是否为对称二叉树)
题目(力扣):
观察题目,只需判断该二叉树是否对称。
判断二叉树是否对称,就可以换位去判断该二叉树的左子树和右子树是否对称。
这时就可以写一个辅助函数来方便判断。
该函数是判断两颗树是否镜像对称,这时就会发现,我们需要的这个函数和判断两棵树是否相等非常相似,只需改变一些条件,(判断树是否相等是左节点的值等于另一棵树左节点的值,右节点的值等于另一棵树右节点的值而镜像则是相反,即左节点的值等于另一棵树右节点的值,右节点的值等于另一棵树左节点的值)
判断两树是否相等:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL)return true;else if (p == NULL || q == NULL)return false;else if (p->val != q->val)return false;elsereturn isSameTree(p->left, q->left)&& isSameTree(p->right, q->right);
}而判断两树是否镜像对称:
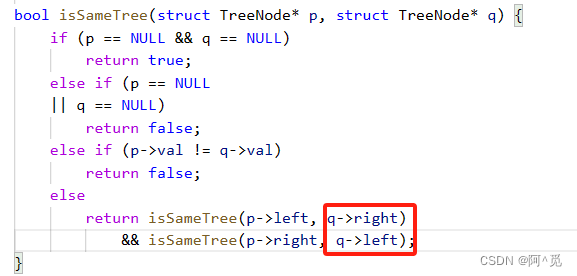
只有这两处地方有改变。
其余地方一直相同。
剩余的isSymmetric函数中就是简单的判断了

完整代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL)return true;else if (p == NULL || q == NULL)return false;else if (p->val != q->val)return false;elsereturn isSameTree(p->left, q->right)&& isSameTree(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root) {if(!root)return true;if((!root->left && root->right) || (!root->right && root->left))return false;else if(root->left && root->right)return isSameTree(root->left,root->right);elsereturn true;
}题目的提交:
相关文章:

二叉树(判断是否为对称二叉树)
题目(力扣): 观察题目,只需判断该二叉树是否对称。 判断二叉树是否对称,就可以换位去判断该二叉树的左子树和右子树是否对称。 这时就可以写一个辅助函数来方便判断。 该函数是判断两颗树是否镜像对称,这…...

STM32开发学习(地址映射)
LED灯代码: #define PERIPH_BASE ((unsigned int)0x40000000)#define AHB1PERIPH_BASE (PERIPH_BASE 0x00020000)#define GPIOF_BASE (AHB1PERIPH_BASE 0x1400)#define GPIOF_MODER *(unsigned int*)(GPIOF_BASE0x00) #define GPIOF_BSRR *(uns…...
 =E(X) + E(Y))
证明E(X+Y) =E(X) + E(Y)
E(XY) E(X) E(Y)的成立是不需要X和Y相互独立的!!! 离散型随机变量 E ( X Y ) ∑ i 1 n ∑ j 1 m ( x i y j ) P { X x i , Y y j } ∑ i 1 n ∑ j 1 m x i P { X x i , Y y j } ∑ i 1 n ∑ j 1 m y j P { X x i , Y y j …...

ClickHouse入门手册1.0
1、数据类型 1.1 整数类型: ClickHouse中整型数据均为固定长度(可以设置长度参数,但是会被忽略),整型包括有符号整型和无符号整型。 有符号整型:Int8,Int16,Int32,Int64,Int128,Int256 无符号整型:UInt8,UInt16,UI…...
10个火爆的设计素材网站推荐
所谓聪明的女人没有米饭很难做饭,设计师也是如此。如何找到优秀的设计材料是每个设计师的痛点,国内材料网站收费,但也限制使用范围和期限,大多数外国设计网站不能打开或需要特殊互联网使用,有一定的安全风险。 作为一…...
SQL注入 - CTF常见题型
文章目录 题型一 ( 字符型注入 )题型二 ( 整数型注入 )题型三 ( 信息收集SQL注入)题型四 ( 万能密码登录 )题型五 ( 搜索型注入文件读写 )题型六 (…...
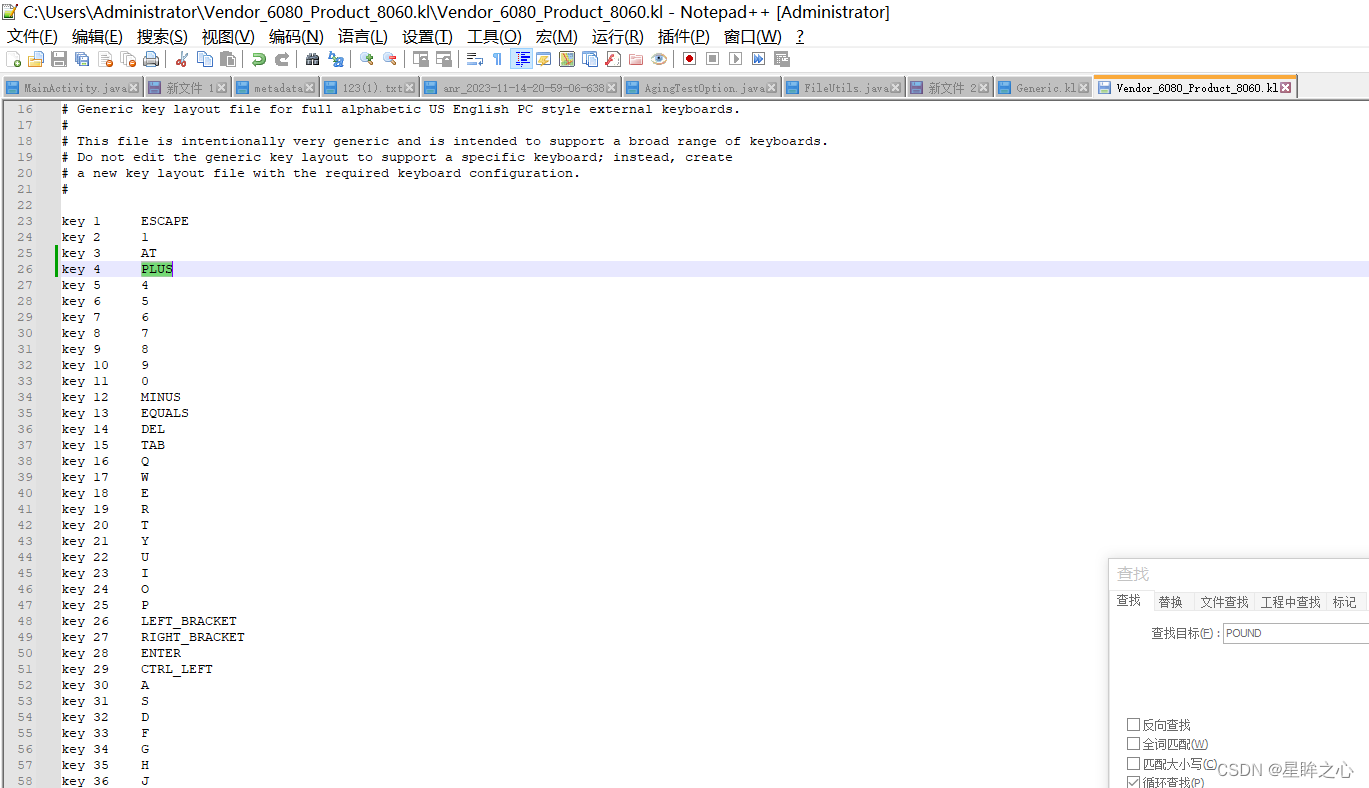
android keylayout键值适配
1、通过getevent打印查看当前keyevent数字对应事件和物理码 2、dumpsys input 查看输入事件对应的 KeyLayoutFile: /system/usr/keylayout/Vendor_6080_Product_8060.kl 3、通过物理码修改键值映射,修改/system/usr/keylayout/目录下的文件...

python读取excel自动化生成sql建表语句和java实体类字段
1、首先准备一个excel文件: idtypenameidint学号namestring姓名ageint年龄sexstring性别weightdecimal(20,4)体重scoredecimal(20,4)分数 2、直接生成java字段和注释: import pandas as pddf pd.read_excel(test.xlsx, sheet_nameSheet1)for i in ran…...
Unity求向量A在平面L上的投影向量
如题:求向量A在平面L上的投影向量(图左) 即求 其实等价于求向量,那在中,,所以只需要求即可 而就是在平面L的法向量的投影坐标,所以代码就是 /// <summary>/// 求向量A在平面B上的投影向量/// </summary>/// <para…...

人机交互2——任务型多轮对话的控制和生成
1.自然语言理解模块 2.对话管理模块 3.自然语言生成模块...

【数据结构】八大排序 (三)
目录 前言: 快速排序 快速排序非递归实现 快速排序特性总结 归并排序 归并排序的代码实现 归并排序的特性总结 计数排序 计数排序的代码实现 计数排序的特性总结 前言: 前文快速排序采用了递归实现,而递归会开辟函数栈帧࿰…...
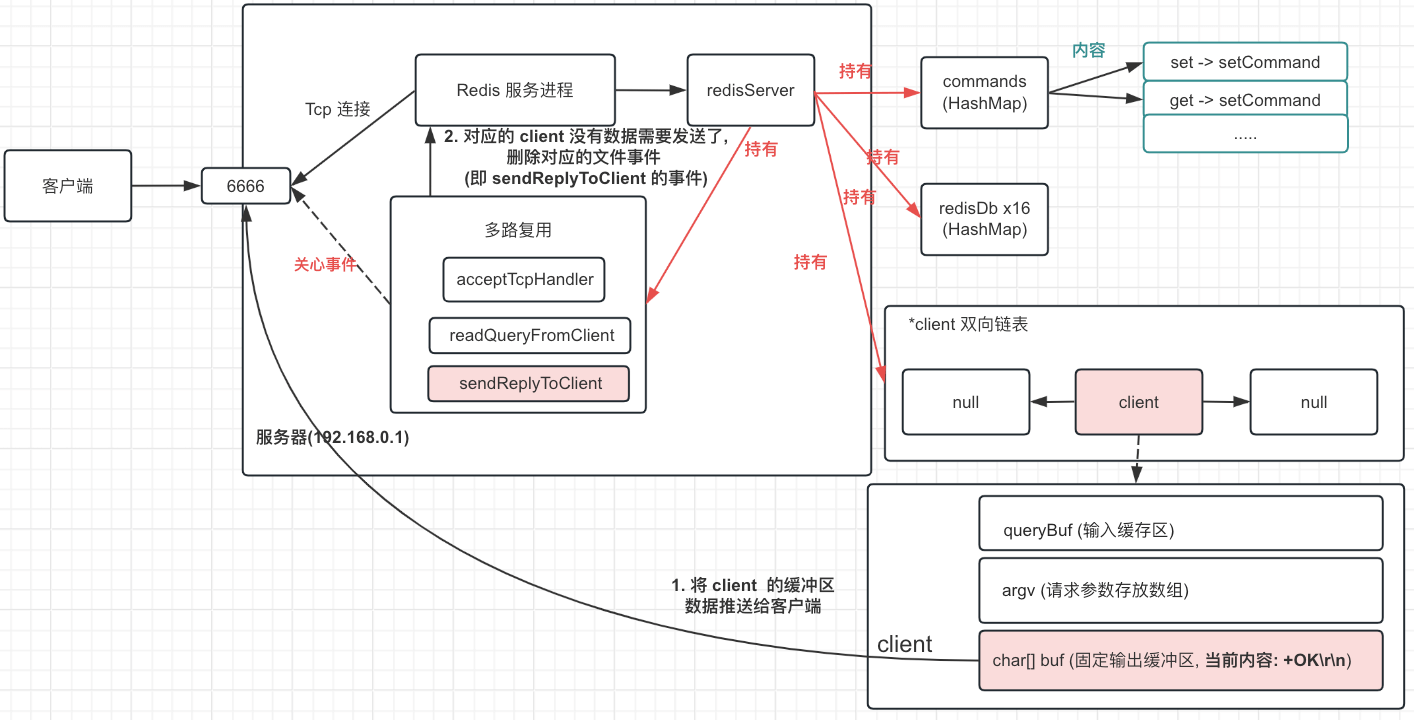
Redis 命令处理过程
我们知道 Redis 是一个基于内存的高性能键值数据库, 它支持多种数据结构, 提供了丰富的命令, 可以用来实现缓存、消息队列、分布式锁等功能。 而在享受 Redis 带来的种种好处时, 是否曾好奇过 Redis 是如何处理我们发往它的命令的呢? 本文将以伪代码的形式简单分析…...

python爬虫进阶教程之如何正确的使用cookie
文章目录 前言一、获取cookie二、程序实现三、动态获取cookie四、其他关于Python爬虫技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③Python小游戏源码五、面试资料六、Pytho…...

【hacker送书第4期】推荐4本Java必读书籍(各送一本)
第4期图书推荐 Java从入门到精通(第7版)内容简介参与方式 项目驱动零基础学Java内容简介参与方式 深入理解Java高并发编程内容简介参与方式 Java编程讲义内容简介参与方式 Java从入门到精通(第7版) 内容简介 《Java从入门到精通&…...

[密码学]DES
先声明两个基本概念 代换(substitution),用别的元素代替当前元素。des的s-box遵循这一设计。 abc-->def 置换(permutation),只改变元素的排列顺序。des的p-box遵循这一设计。 abc-->bac DES最核心的算法就是…...

15个超级实用的Python操作,肯定有你意想不到的!
文章目录 1)映射代理(不可变字典)2)dict 对于类和对象是不同的3) any() 和 all()4) divmod()5) 使用格式化字符串轻松检查变量6) 我们可以将浮点数转换为比率7) 用globals()和locals()显示现有的全局/本地变量8) import() 函数9) …...

GitHub上8个强烈推荐的 Python 项目
文章目录 前言1. Manim2. DeepFaceLab3. Airflow4. GPT-25. XSStrike6. 谷歌图片下载7. Gensim8. SocialMapper总结关于Python技术储备一、Python所有方向的学习路线二、Python基础学习视频三、精品Python学习书籍四、Python工具包项目源码合集①Python工具包②Python实战案例③…...

什么是依赖倒置原则
1、什么是依赖倒置原则 依赖倒置原则(Dependency Inversion Principle,DIP)是指高层模块不应该依赖于低层模块,它们都应该依赖于抽象。换句话说,具体类之间的依赖关系应该尽可能减少,而抽象类或接口之间的…...
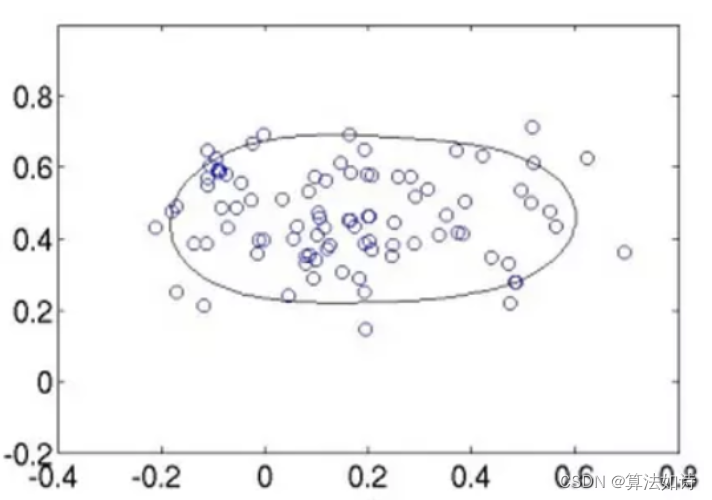
异常数据检测 | Python实现oneclassSVM模型异常数据检测
支持向量机(SVM)的异常检测 SVM通常应用于监督式学习,但OneClassSVM[8]算法可用于将异常检测这样的无监督式学习,它学习一个用于异常检测的决策函数其主要功能将新数据分类为与训练集相似的正常值或不相似的异常值。 OneClassSVM OneClassSVM的思想来源于这篇论文[9],SVM使用…...
)
using meta-SQL 使用元SQL (3)
%FirstRows Syntax %FirstRows(n) Description The %FirstRows meta-SQL variable is replaced by database-specific SQL syntax to optimize retrieval of n rows. Depending on the database, this variable optimizes: FirstRows meta-SQL变量被特定于数据库的SQL语法…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
