Leetcode.974 和可被 K 整除的子数组
题目链接
Leetcode.974 和可被 K 整除的子数组
rating : 1676
题目描述
给定一个整数数组 n u m s nums nums 和一个整数 k k k ,返回其中元素之和可被 k k k 整除的(连续、非空) 子数组 的数目。
子数组 是数组的 连续 部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:
有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:
输入: nums = [5], k = 9
输出: 0
提示:
- 1 ≤ n u m s . l e n g t h ≤ 3 ∗ 1 0 4 1 \leq nums.length \leq 3 * 10^4 1≤nums.length≤3∗104
- − 1 0 4 ≤ n u m s [ i ] ≤ 1 0 4 -10^4 \leq nums[i] \leq 10^4 −104≤nums[i]≤104
- 2 ≤ k ≤ 1 0 4 2 \leq k \leq 10^4 2≤k≤104
解法:前缀和 + 哈希表
我们假设 [ j , i ] [j,i] [j,i] 区间的子数组元素和可以被 k k k 整除,即 :
( n u m s [ j ] + n u m s [ j + 1 ] + . . . + n u m s [ i − 1 ] + n u m s [ i ] ) m o d k = 0 (nums[j] + nums[j + 1] + ... + nums[i-1] + nums[i])\ mod\ k = 0 (nums[j]+nums[j+1]+...+nums[i−1]+nums[i]) mod k=0
我们用 s u m sum sum 表示 n u m s nums nums 的前缀和数组,可将上式转换为:
( s u m [ i ] − s u m [ j − 1 ] ) m o d k = 0 (sum[i] - sum[j-1])\ mod\ k = 0 (sum[i]−sum[j−1]) mod k=0
再转换一下得到:
s u m [ j − 1 ] m o d k = s u m [ i ] m o d k sum[j-1]\ mod\ k= sum[i]\ mod\ k sum[j−1] mod k=sum[i] mod k
那么以 n u m s [ i ] nums[i] nums[i] 为结尾的数组,我们只需要统计前面等于 s u m [ j − 1 ] m o d k sum[j-1]\ mod\ k sum[j−1] mod k 也就是 s u m [ i ] m o d k sum[i]\ mod\ k sum[i] mod k 的数量 t t t 即可。
那么这个 t t t 就是以 n u m s [ i ] nums[i] nums[i] 为结尾的数组中 和能被 k k k 整除的子数组的数量。
我们只需要对每一个 n u m s [ i ] nums[i] nums[i] 都加上 t t t 即可,这样我们就可以统计出所有的 和能被 k k k 整除的子数组的数量。
在实现上,我们使用哈希表来记录前缀和出现的次数。初始时,和为 0 0 0 ,也需要统计它的出现次数,即 { 0 , 1 } \{ 0 , 1 \} {0,1}。
注意:由于 n u m s nums nums 中存在负数,所以 s u m m o d k sum\ mod\ k sum mod k 仍然有可能是负数,所以我们要将其转换为正数,即:
k e y = ( s u m m o d k + k ) m o d k key = (sum\ mod\ k + k)\ mod\ k key=(sum mod k+k) mod k
时间复杂度: O ( n ) O(n) O(n)
C++代码:
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {int n = nums.size();int ans = 0 , sum = 0;unordered_map<int,int> cnt{{0,1}};for(int i = 0;i < n;i++){sum += nums[i];auto key = (sum % k + k) % k;ans += cnt[key];cnt[key]++;}return ans;}
};
相关文章:

Leetcode.974 和可被 K 整除的子数组
题目链接 Leetcode.974 和可被 K 整除的子数组 rating : 1676 题目描述 给定一个整数数组 n u m s nums nums 和一个整数 k k k ,返回其中元素之和可被 k k k 整除的(连续、非空) 子数组 的数目。 子数组 是数组的 连续 部分。 示例 1&…...
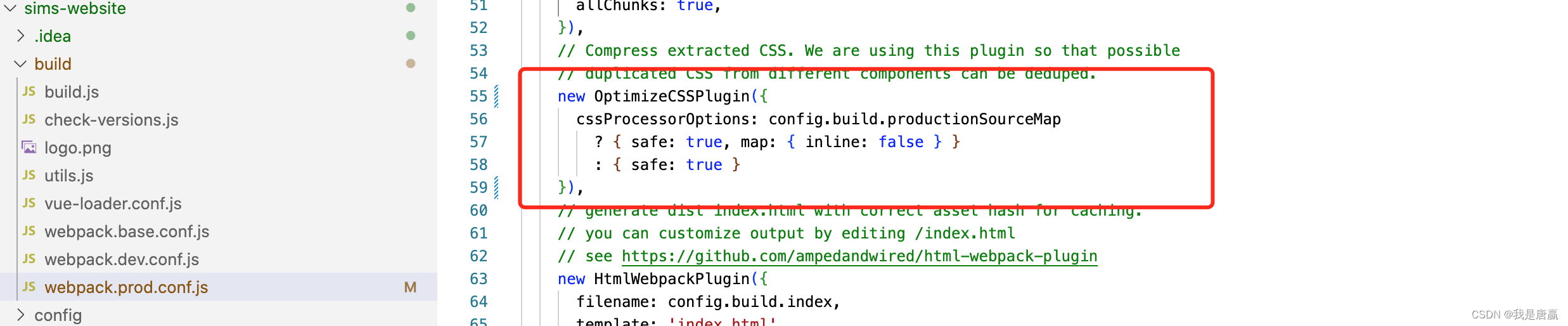
Vue打包错误UnhandledPromiseRejectionWarning: CssSyntaxError
错误详情如下: building for production...Error processing file: static/css/app.3d5caae7aaba719754d7d5c30b864551.css (node:33011) UnhandledPromiseRejectionWarning: CssSyntaxError: /Users/yt/Documents/BM/sims-plus/sims-website/static/css/app.3d5caa…...
鸿蒙系统扫盲(三):鸿蒙开发用什么语言?
1.两种开发方向 我们常说鸿蒙开发,但是其实鸿蒙开发分为两个方向: 一个是系统级别的开发,比如驱动,内核和框架层的开发,这种开发以C/C为主 还有一个是应用级别的开发,在API7以及以下,还是支持…...

linux 中vmalloc实现简述
vmalloc 用途 vmalloc只用于内核模块的逻辑地址分配,也就是说它的逻辑地址是挂在init_mm的pgd页表上的。它可将几段不连续物理区域合并分配一个连续逻辑区域。主要用于内核和驱动。 vmalloc 实现 入口在__vmalloc_node_range。 首先分配一个vm_struct,…...

homeassistant 随笔
1.使用mushroom-strategy自动生成ui,隐藏中文ares,名字为区域的拼音,例如显示厨房则真实名字为chu_fang 隐藏图片中的工作室 代码为:...

带大家做一个,易上手的家常炒鸡蛋
想做这道菜 先准备五个鸡蛋 然后将鸡蛋打到碗里面 然后 加小半勺盐 这个看个人喜好 放多少都没问题 不要太咸就好 将鸡蛋搅拌均匀 起锅烧油 油温热了之后 放三个干辣椒进去炒 干辣椒烧黑后 捞出来 味道就留在油里了 然后 倒入鸡蛋液 翻炒 注意翻炒 不要粘锅底 或者 一面糊…...

芒格传奇落幕!生前最后一次谈论比特币,说了什么?
当地时间11月28日,知名投资公司伯克希尔哈撒韦发布声明,公司董事会副主席查理芒格(Charlie Munger)于当天早上在美国加利福尼亚州的一家医院去世,终年99岁,距离其百岁生日仅剩1个月。 巴菲特在一份声明中表示:“没有查…...
Springboot如何快速生成分页展示以及统计条数
这是表结构: 前置知识: 分页查询公式(): -- 推导一个公式 -- select * from emp -- order by empno -- limit 每页显示记录数 * (第几页-1),每页显示记录数 统计条数公式: select count…...

数据结构:图文详解顺序表的各种操作(新增元素,查找元素,删除元素,给指定位置元素赋值)
目录 一.顺序表的概念 二.顺序表的实现 新增元素 默认尾部新增 指定位置添加元素 查找元素 查找是否存在 查找元素对应的位置 查找指定位置对应的元素 删除元素 获取顺序表长度 清空顺序表 一.顺序表的概念 在线性数据结构中,我们一般分为俩类…...
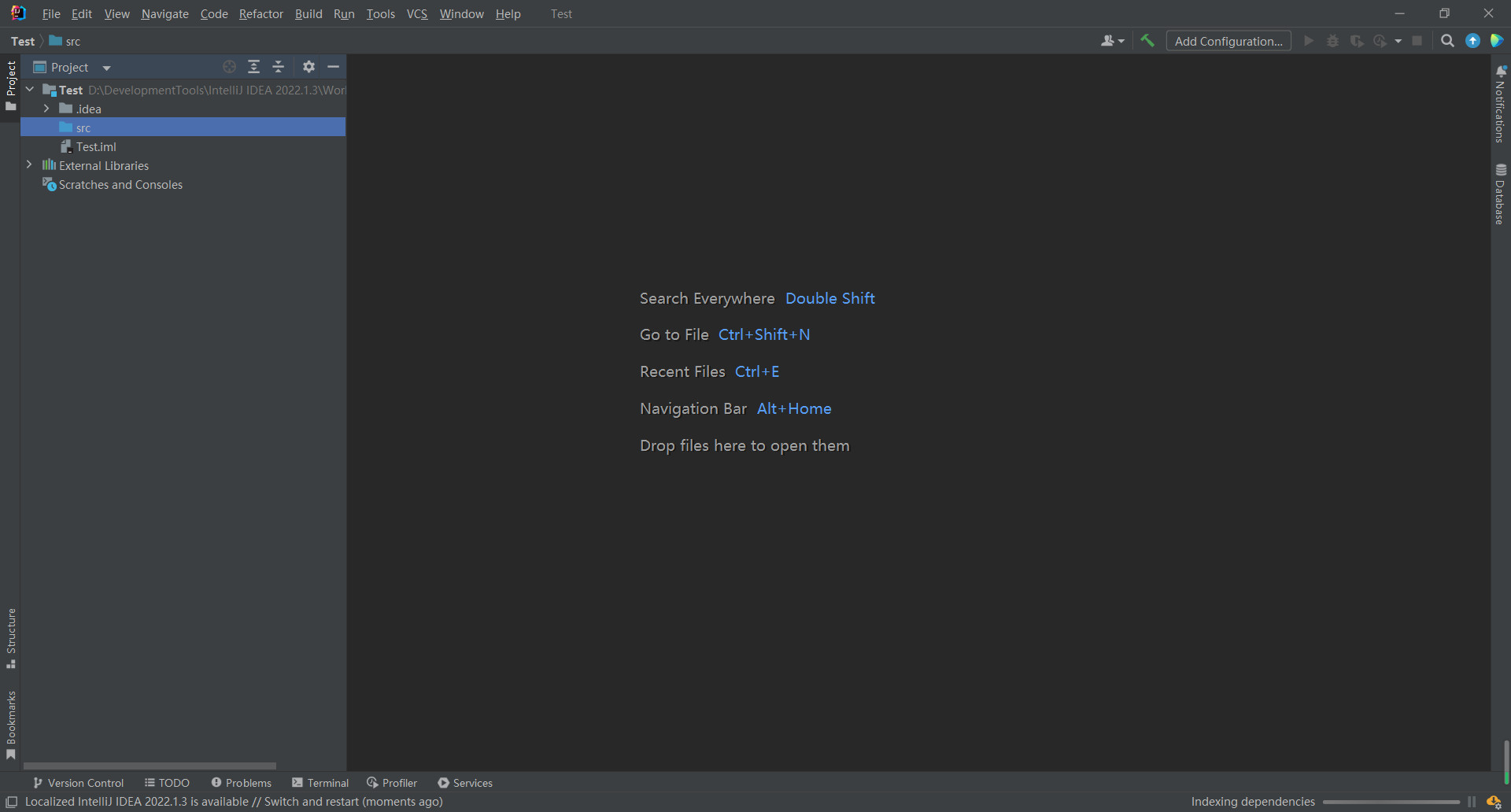
2023 年 IntelliJ IDEA下载、安装教程,附详细图文
大家好,今天为大家带来的是 2023年 IntelliJ IDEA 下载、安装教程,超详细的图文教程,亲测可用。 文章目录 1 IDEA 下载2 IDEA 安装3 IDEA 使用4 快捷键新手必须掌握:Ctrl:Alt:Shift:Ctrl Alt&a…...
C++——解锁string常用接口
目录 string::npos; 1.测试string容量相关的接口: 1.1 string::size() 1.2 string::clear() 1.3 string::resize() 1.4 string::erase() 1.5 string::reserve() 保留 1.6 std::string::shrink_to_fit 2.string数据插入删除相关的接口 2.1 std::string::pus…...

Stable Video Diffusion(SVD)参数使用教程
Stable Video Diffusion(SVD)安装和测试 官网 github | https://github.com/Stability-AI/generative-modelsHugging Face | https://huggingface.co/stabilityai/stable-video-diffusion-img2vid-xtPaper | https://stability.ai/research/stable-vid…...

【传智杯】排排队、小卡与质数 2、1024 程序员节发橙子题解
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙请不要相信胜利就像山坡上的蒲公英一样唾手…...

Oracle
1.解释冷备份和热备份的不同点以及各自的优点 冷备份 发生在数据库已经正常关闭的情况下,将关键性文件拷贝到另外位置的一种说法。适用于所有模式的数据库。 优点 是非常快速的备份方法(只需拷贝文件)容易归档(简单拷贝即可&a…...
2023年c语言程序设计大赛
7-1 这是一道送分题 为了让更多的同学参与程序设计中来,这里给同学们一个送分题,让各位感受一下程序设计的魅力,并祝贺各位同学在本次比赛中取得好成绩。 注:各位同学只需将输入样例里的代码复制到右侧编译器,然后直…...
:spu管理页面的新增和修改)
9.vue3项目(九):spu管理页面的新增和修改
目录 一、SPU和SKU概念 二、SPU静态搭建 1.代码编辑 2.效果展示 三、封装接口以及出参入参...

人工智能:让生活更便捷、更智能——探讨人工智能在生活中的作用与挑战
文章目录 前言人工智能的定义与分类人工智能的领域一、智能语音助手改变日常生活二、智能驾驶带来出行革命三、人工智能在医疗健康领域的应用四、教育领域的人工智能创新 人工智能的应用生活方面的影响工作方面的影响 应对AI带来的挑战后记 前言 人工智能相关的领域࿰…...
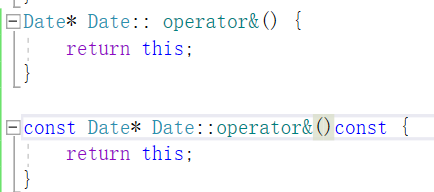
【C++】类和对象——const修饰成员函数和取地址操作符重载
在上篇博客中,我们已经对于日期类有了较为全面的实现,但是,还有一个问题,比如说,我给一个const修饰的日期类的对象 这个对象是不能调用我们上篇博客写的函数的,因为&d1是const Date*类型的ÿ…...
express+mySql实现用户注册、登录和身份认证
expressmySql实现用户注册、登录和身份认证 注册 注册时需要对用户密码进行加密入库,提高账户的安全性。用户登录时再将密码以相同的方式进行加密,再与数据库中存储的密码进行比对,相同则表示登录成功。 安装加密依赖包bcryptjs cnpm insta…...
加载数据集)
【PyTorch】(二)加载数据集
文章目录 1. 创建数据集1.1. 直接继承Dataset类1.2. 使用TensorDataset类 2. 加载数据集3. 将数据转移到GPU 1. 创建数据集 主要是将数据集读入内存,并用Dataset类封装。 1.1. 直接继承Dataset类 必须要重写__getitem__方法,用于根据索引获得相应样本…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
