决策树学习
1. 背景
DT决策树是一种基本的分类与回归方法,其学习时,利用训练数据,根据损失函数最小化原则建立DT模型。
分类DT主要优点:模型具有可读性,分类速度快。
由DT树的根结点到叶结点的每一条路径构建一条规则,即组合特征,路径上内部结点
的特征对应着规则的条件,而叶结点的类对应着规则的结论。这些路径互斥且完备。
DT学习通常包括3个步骤:特征选择、DT的生成与DT的修剪。DT的生成只考虑局部最优,而DT的剪枝则考虑全局最优。
DT学习是由训练数据集估计条件概率模型,其损失函数通常是正则化的极大似然函数,其策略是损失函数为目标函数的最小化。
2. 特征选择
特征选择在于选取对训练数据具有分类能力的特征,这样可以提高DT学习的效率。通常特征选择的准则是信息增益或信息增益比。
2.1 熵
随机变量X的熵定义为 (对数以2为底时,熵的单位叫bit;以e为底时,熵的单位叫nat)。
其中 ,i=1,2,...,n
熵只依赖于X的分布,与X的取值无关,且 。
2.2 条件熵
H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。
即X给定条件下Y的条件概率分布的熵对X的数学期望
其中令0log0=0
信息增益表示,得知特征X的信息而使得类Y的信息的不确定性减少的程度。
2.3 信息增益及其计算
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差(亦叫类与特征的互信息)。
(1)计算数据集D的经验熵H(D)
表示对数据集D进行分类的不确定性。
(2)计算特征A对数据集D的经验条件熵H(D|A)
表示在特征A给定的条件下对数据集D进行分类的不确定性。
(3)计算信息增益
表示由于特征A而使得对数据集D的分类的不确定性减少的程度。
2.4 信息增益比
信息增益存在偏向于选择取值较多的特征的问题。使用信息增益比可以对这一问题
进行校正。
定义:信息增益g(D,A)与训练集D关于特征A的值的熵之比。
即
其中,n为特征A取值的个数。
3. DT的生成
3.1 ID3算法
ID3算法的核心是在DT各个结点上应用信息增益准则选择特征,递归地构建DT。具体方法如下:
从根结点开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点;再对子结点递归地调用以上方法,构建DT;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个DT。
ID3相当于用极大似然法进行概率模型的选择,但其只有树的生成,所以该算法生成的树
容易产生过拟合。
3.2 C4.5算法
C4.5算法对ID3算法进行了改进,在生成过程中,用信息增益比来选择特征。
4. DT的剪枝
剪枝(pruning)是将已生成的树进行简化的过程,即从已生成的树上裁掉一些子树或叶结点,
并将其根结点或父结点作为新的叶结点,从而简化分类树模型。DT的剪枝往往通过极小化DT整体的损失函数来实现。
DT学习的损失函数可以定义为: (
)
其中
表示模型对训练数据的预测误差;
为叶结点t上的经验熵。
|T|为树T的叶结点个数(即模型复杂度),t是树T的叶结点,该叶结点有个样本点,其中k类样本点有
个。
参数
控制着预测误差与模型复杂度之间的影响,较小的
促使选择较复杂的模型。
剪枝就是当确定时,选择损失函数最小的模型(子树)。
DT生成学习局部的模型(只考虑了通过提高信息增益对训练数据进行更好的拟合),DT剪枝学习整体的模型(通过优化损失函数还考虑了减小模型复杂度)。
利用损失函数最小原则进行剪枝就是用正则化的极大似然估计进行模型选择。
5. CART算法
分类与回归树CART(classification and regression tree)模型既可以用于分类也可以用于回归(其假设DT是二叉树)。
5.1 CART生成
基于训练数据集生成DT,生成的DT要尽量大;
DT的生成就是递归地构建二叉DT的过程,对回归树用平方误差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
5.1.1 回归树的生成
可以用平方误差来表示回归树对于训练数据的预测误差。
5.1.2 分类树的生成
分类树用基尼指数选择最优特征,同时决定该特征的最优二值切分点(选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点)。
样本集合D的基尼指数
特征A条件下集合D的基尼指数
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数与熵相似,其值越大,样本集合的不确定性也就越大。
5.2 CART剪枝
用验证数据集对已生成的树进行剪枝并选择最优子树,这时用损失函数最小作为剪枝的标准。CART剪枝算法从“完全生长”的DT的底端剪去一些子树,使DT变得简单,从而能够对未知数据有更准确的预测。
step.1 剪枝,形成一个子树序列;
step.2 在剪枝得到子树序列中通过交叉验证选取最优子树。
相关文章:
决策树学习
1. 背景 DT决策树是一种基本的分类与回归方法,其学习时,利用训练数据,根据损失函数最小化原则建立DT模型。 分类DT主要优点:模型具有可读性,分类速度快。 由DT树的根结点到叶结点的每一条路径构建一条规则&…...

如何在Ubuntu系统上安装Git
简单介绍 Git是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目。Git是Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源码的版本控制软件。Git 与常用的版本控制工具CVS,Subversion 等不同,它采用了分布式版…...

Leetcode.974 和可被 K 整除的子数组
题目链接 Leetcode.974 和可被 K 整除的子数组 rating : 1676 题目描述 给定一个整数数组 n u m s nums nums 和一个整数 k k k ,返回其中元素之和可被 k k k 整除的(连续、非空) 子数组 的数目。 子数组 是数组的 连续 部分。 示例 1&…...
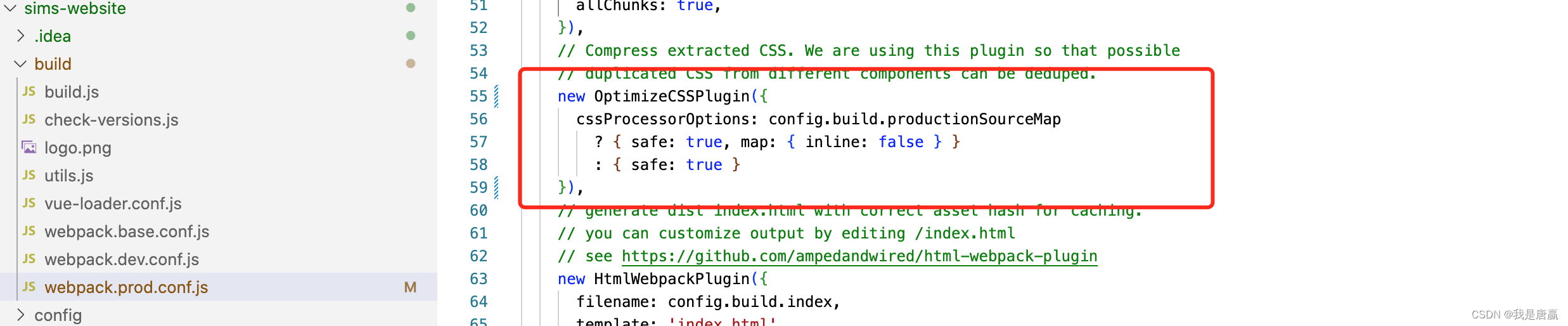
Vue打包错误UnhandledPromiseRejectionWarning: CssSyntaxError
错误详情如下: building for production...Error processing file: static/css/app.3d5caae7aaba719754d7d5c30b864551.css (node:33011) UnhandledPromiseRejectionWarning: CssSyntaxError: /Users/yt/Documents/BM/sims-plus/sims-website/static/css/app.3d5caa…...
鸿蒙系统扫盲(三):鸿蒙开发用什么语言?
1.两种开发方向 我们常说鸿蒙开发,但是其实鸿蒙开发分为两个方向: 一个是系统级别的开发,比如驱动,内核和框架层的开发,这种开发以C/C为主 还有一个是应用级别的开发,在API7以及以下,还是支持…...

linux 中vmalloc实现简述
vmalloc 用途 vmalloc只用于内核模块的逻辑地址分配,也就是说它的逻辑地址是挂在init_mm的pgd页表上的。它可将几段不连续物理区域合并分配一个连续逻辑区域。主要用于内核和驱动。 vmalloc 实现 入口在__vmalloc_node_range。 首先分配一个vm_struct,…...

homeassistant 随笔
1.使用mushroom-strategy自动生成ui,隐藏中文ares,名字为区域的拼音,例如显示厨房则真实名字为chu_fang 隐藏图片中的工作室 代码为:...

带大家做一个,易上手的家常炒鸡蛋
想做这道菜 先准备五个鸡蛋 然后将鸡蛋打到碗里面 然后 加小半勺盐 这个看个人喜好 放多少都没问题 不要太咸就好 将鸡蛋搅拌均匀 起锅烧油 油温热了之后 放三个干辣椒进去炒 干辣椒烧黑后 捞出来 味道就留在油里了 然后 倒入鸡蛋液 翻炒 注意翻炒 不要粘锅底 或者 一面糊…...

芒格传奇落幕!生前最后一次谈论比特币,说了什么?
当地时间11月28日,知名投资公司伯克希尔哈撒韦发布声明,公司董事会副主席查理芒格(Charlie Munger)于当天早上在美国加利福尼亚州的一家医院去世,终年99岁,距离其百岁生日仅剩1个月。 巴菲特在一份声明中表示:“没有查…...
Springboot如何快速生成分页展示以及统计条数
这是表结构: 前置知识: 分页查询公式(): -- 推导一个公式 -- select * from emp -- order by empno -- limit 每页显示记录数 * (第几页-1),每页显示记录数 统计条数公式: select count…...

数据结构:图文详解顺序表的各种操作(新增元素,查找元素,删除元素,给指定位置元素赋值)
目录 一.顺序表的概念 二.顺序表的实现 新增元素 默认尾部新增 指定位置添加元素 查找元素 查找是否存在 查找元素对应的位置 查找指定位置对应的元素 删除元素 获取顺序表长度 清空顺序表 一.顺序表的概念 在线性数据结构中,我们一般分为俩类…...
2023 年 IntelliJ IDEA下载、安装教程,附详细图文
大家好,今天为大家带来的是 2023年 IntelliJ IDEA 下载、安装教程,超详细的图文教程,亲测可用。 文章目录 1 IDEA 下载2 IDEA 安装3 IDEA 使用4 快捷键新手必须掌握:Ctrl:Alt:Shift:Ctrl Alt&a…...
C++——解锁string常用接口
目录 string::npos; 1.测试string容量相关的接口: 1.1 string::size() 1.2 string::clear() 1.3 string::resize() 1.4 string::erase() 1.5 string::reserve() 保留 1.6 std::string::shrink_to_fit 2.string数据插入删除相关的接口 2.1 std::string::pus…...

Stable Video Diffusion(SVD)参数使用教程
Stable Video Diffusion(SVD)安装和测试 官网 github | https://github.com/Stability-AI/generative-modelsHugging Face | https://huggingface.co/stabilityai/stable-video-diffusion-img2vid-xtPaper | https://stability.ai/research/stable-vid…...

【传智杯】排排队、小卡与质数 2、1024 程序员节发橙子题解
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙请不要相信胜利就像山坡上的蒲公英一样唾手…...

Oracle
1.解释冷备份和热备份的不同点以及各自的优点 冷备份 发生在数据库已经正常关闭的情况下,将关键性文件拷贝到另外位置的一种说法。适用于所有模式的数据库。 优点 是非常快速的备份方法(只需拷贝文件)容易归档(简单拷贝即可&a…...
2023年c语言程序设计大赛
7-1 这是一道送分题 为了让更多的同学参与程序设计中来,这里给同学们一个送分题,让各位感受一下程序设计的魅力,并祝贺各位同学在本次比赛中取得好成绩。 注:各位同学只需将输入样例里的代码复制到右侧编译器,然后直…...
:spu管理页面的新增和修改)
9.vue3项目(九):spu管理页面的新增和修改
目录 一、SPU和SKU概念 二、SPU静态搭建 1.代码编辑 2.效果展示 三、封装接口以及出参入参...

人工智能:让生活更便捷、更智能——探讨人工智能在生活中的作用与挑战
文章目录 前言人工智能的定义与分类人工智能的领域一、智能语音助手改变日常生活二、智能驾驶带来出行革命三、人工智能在医疗健康领域的应用四、教育领域的人工智能创新 人工智能的应用生活方面的影响工作方面的影响 应对AI带来的挑战后记 前言 人工智能相关的领域࿰…...
【C++】类和对象——const修饰成员函数和取地址操作符重载
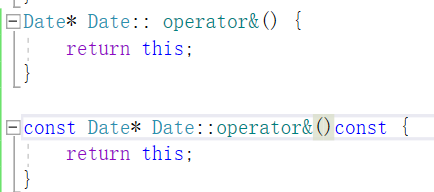
在上篇博客中,我们已经对于日期类有了较为全面的实现,但是,还有一个问题,比如说,我给一个const修饰的日期类的对象 这个对象是不能调用我们上篇博客写的函数的,因为&d1是const Date*类型的ÿ…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
