EM@常见平面曲线的方程的不同表示方式
文章目录
- abstract
- 常见曲线的不同形式
- 小结:一览表
- 分析
- 圆锥曲线的极坐标方程
- 非标准位置的圆锥曲线参数方程
- 应用比较
- refs
abstract
- 常见平面曲线的方程的不同表示方式
常见曲线的不同形式
- 下面以平面曲线为对象讨论
- 参数方程通常是对普通方程的补充和增强,曲线的普通方程(直角坐标方程)和其参数方程通常在直角坐标系中讨论,都涉及到 x , y x,y x,y
- 而曲线的极坐标方程,是以和直角坐标截然不同的坐标系,尤其擅长表示的曲线类型,利用直角坐标和极坐标转换公式,可以完成同一曲线的普通方程和极坐标方程形式转换
- 在应用中,处理方程形式的变换,还要注意定义域或变量取值范围的等价转换,例如
- x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1, ( x , y ⩾ 0 ) (x,y\geqslant{0}) (x,y⩾0)转换为极坐标表示为: ρ = 1 \rho=1 ρ=1, θ ∈ [ 0 , π 2 ] \theta\in[0,\frac{\pi}{2}] θ∈[0,2π],都表示的是 1 4 \frac{1}{4} 41圆弧,
- 而对应的参数方程为 x = cos θ x=\cos\theta x=cosθ; y = sin θ y=\sin\theta y=sinθ, θ ∈ [ 0 , π 2 ] \theta\in[0,\frac{\pi}{2}] θ∈[0,2π]
- x x x在该段圆弧的取值范围 [ 0 , 1 ] [0,1] [0,1],因此 x = cos θ ∈ [ 0 , 1 ] x=\cos\theta\in[0,1] x=cosθ∈[0,1],解得 θ ∈ [ 0 , π 2 ] \theta\in[0,\frac{\pi}{2}] θ∈[0,2π]
- 直角坐标和极坐标转换公式是在极坐标的极点和直角坐标原点重合的情形
- x = ρ cos θ x=\rho\cos\theta x=ρcosθ; y = ρ sin θ y=\rho\sin\theta y=ρsinθ
- 上述转换公式不能滥用,有时极点不和直角坐标系的原点重合,就不能直接代入上述公式,需要调整
- 极点的位置根据问题的需要建立在合适的位置对于极坐标方程的形式是重要的,而对比较简单的情形,通常建立在直角坐标系的原点上
小结:一览表
| 曲线 | 普通方程 | 极坐标方程 | 参数方程 |
|---|---|---|---|
| 圆心在 ( 0 , 0 ) (0,0) (0,0) | x 2 + y 2 = R 2 x^2+y^2=R^2 x2+y2=R2 | ρ = R \rho=R ρ=R | x = R cos θ x=R\cos\theta x=Rcosθ; y = R sin θ y=R\sin\theta y=Rsinθ, ( θ ∈ [ 0 , 2 π ) ) (\theta\in[0,2\pi)) (θ∈[0,2π)) |
| 圆心在 ( a , b ) (a,b) (a,b) | ( x − a ) 2 + ( y − b ) 2 = R 2 (x-a)^2+(y-b)^2=R^2 (x−a)2+(y−b)2=R2 | ( ρ cos θ − a ) 2 + ( ρ sin θ − b ) 2 = R 2 (\rho\cos{\theta}-a)^2+(\rho\sin\theta-b)^2=R^2 (ρcosθ−a)2+(ρsinθ−b)2=R2 | x = a + R cos θ x=a+R\cos\theta x=a+Rcosθ ; y = b + R sin θ y=b+R\sin\theta y=b+Rsinθ; ( ( θ ∈ [ 0 , 2 π ) ) ((\theta\in[0,2\pi)) ((θ∈[0,2π)) |
| 圆心在 ( a , 0 ) (a,0) (a,0)且半径 R = a R=a R=a | ( x − a ) 2 + y 2 = a 2 (x-a)^2+y^2=a^2 (x−a)2+y2=a2 | ρ = 2 a cos θ \rho=2a\cos\theta ρ=2acosθ | x = a + a cos θ x=a+a\cos\theta x=a+acosθ ; y = a sin θ y=a\sin\theta y=asinθ; ( ( θ ∈ [ 0 , 2 π ) ) ((\theta\in[0,2\pi)) ((θ∈[0,2π)) |
| 圆心在 ( 0 , a ) (0,a) (0,a)且半径 R = a R=a R=a | x 2 + ( y − b ) 2 = a 2 x^2+(y-b)^2=a^2 x2+(y−b)2=a2 | ρ = 2 a sin θ \rho=2a\sin\theta ρ=2asinθ | x = a cos θ x=a\cos\theta x=acosθ ; y = a + a sin θ y=a+a\sin\theta y=a+asinθ; ( ( θ ∈ [ 0 , 2 π ) ) ((\theta\in[0,2\pi)) ((θ∈[0,2π)) |
| 直线 | A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0 | A ρ cos θ + B ρ sin θ + C = 0 A\rho\cos\theta+B\rho\sin\theta+C=0 Aρcosθ+Bρsinθ+C=0 | x = x 0 + B t x=x_0+Bt x=x0+Bt; y = y 0 − A t y=y_0-At y=y0−At ( t ∈ R ) (t\in\mathbb{R}) (t∈R) |
| 以下极点建立在焦点上 | |||
| 椭圆(中心位于 ( 0 , 0 ) (0,0) (0,0)) | x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 a2x2+b2y2=1 | ρ = p 1 − e cos θ \rho=\frac{p}{1-e\cos\theta} ρ=1−ecosθp, ( e < 1 ) (e<1) (e<1) | x = a cos t x=a\cos{t} x=acost; y = b sin t y=b\sin{t} y=bsint; 0 ∈ [ 0 , 2 π ] 0\in[0,2\pi] 0∈[0,2π] |
| 抛物线(顶点位于 ( 0 , 0 ) (0,0) (0,0)) | y 2 = x y^2=x y2=x | ρ = p 1 − e cos θ \rho=\frac{p}{1-e\cos\theta} ρ=1−ecosθp, ( e = 1 ) (e=1) (e=1) | x = 2 p t 2 x=2pt^2 x=2pt2; y = 2 p t y=2pt y=2pt; ( t ∈ R ) (t\in\mathbb{R}) (t∈R) |
| 双曲线(中心位于 ( 0 , 0 ) (0,0) (0,0)) | x 2 a 2 − y 2 b 2 = 1 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 a2x2−b2y2=1 | ρ = p 1 − e cos θ \rho=\frac{p}{1-e\cos\theta} ρ=1−ecosθp, ( e > 1 ) (e>1) (e>1) | x = a sec θ x=a\sec\theta x=asecθ; y = b tan θ y=b\tan\theta y=btanθ; ( θ ∈ [ 0 , 2 π ) , θ ≠ k π + π 2 , k = 0 , 1 ) (\theta\in[0,2\pi),\theta\neq{k\pi}+\frac{\pi}{2},k=0,1) (θ∈[0,2π),θ=kπ+2π,k=0,1) |
分析
-
上表中不是每个方程都常用例如极坐标方程形式复杂或不便于计算,就不常用
-
直线的普通方程有各种各样的形式,一般方程 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0, ( A B ≠ 0 ) (AB\neq{0}) (AB=0)可以表示任意直线
- 其法线方向向量为 ( A , B ) (A,B) (A,B)
- 其方向向量为 ( B , − A ) (B,-A) (B,−A)
-
直线的参数方程也有多种形式
-
从普通方程化为极坐标方程通常是容易的
- 只要将直角坐标和极坐标的转换公式代入普通方程,即可得到极坐标方程
- 而对于简单曲线,还可以从几何特点出发:设曲线上的任意点为 ( ρ , θ ) (\rho,\theta) (ρ,θ),根据曲线几何特点,建立极坐标方程,这比通用的代入转化公式更加直观
- 例如,半径为 R R R,圆心为 ( 0 , 0 ) (0,0) (0,0),可以立马根据几何性质写出极坐标方程为 ρ = 1 \rho=1 ρ=1
-
而普通方程化为参数方程就复杂一些
圆锥曲线的极坐标方程
- 上述表格中给出的是中心在坐标原点的情形下圆锥曲线的极坐标方程
- 将极坐标建立在直角坐标系原点上是不常见的,此时代入坐标转换公式可知,形式复杂,一般不利于使用
非标准位置的圆锥曲线参数方程
-
对于椭圆和双曲线,标准位置指中心在坐标原点的情形
-
利用坐标平移公式,可以得到与非标准位置的圆的类似的参数方程
- 椭圆(中心为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)): x = x 0 + a cos θ x=x_0+a\cos{\theta} x=x0+acosθ; y = y 0 + b sin θ y=y_0+b\sin{\theta} y=y0+bsinθ; θ ∈ [ 0 , 2 π ] \theta\in[{0},{2\pi}] θ∈[0,2π]
- 双曲线(中心为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)): x = x 0 + a sec θ x=x_0+a\sec{\theta} x=x0+asecθ; y = y 0 + b tan θ y=y_0+b\tan{\theta} y=y0+btanθ; θ ∈ [ 0 , 2 π ] \theta\in[{0},{2\pi}] θ∈[0,2π]
- 抛物线(顶点为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)): x = x 0 + 2 p t 2 x=x_0+2pt^2 x=x0+2pt2; y = y 0 + 2 p t y=y_0+2pt y=y0+2pt; t ∈ R t\in\mathbb{R} t∈R
应用比较
- 极坐标方程适合用在 f ( x 2 + y 2 ) f(x^2+y^2) f(x2+y2), f ( y x ) f(\frac{y}{x}) f(xy), f ( x y ) f(\frac{x}{y}) f(yx)这类情形下,可以简化曲线的表示形式,在二重积分的某些和圆有关的区域,用极坐标表示往往是方便的
- 参数方程可以表示一些一般方程那一表示的或者表示形式复杂的曲线或方程
refs
- 极坐标方程
- 圆@圆锥曲线参数方程
相关文章:

EM@常见平面曲线的方程的不同表示方式
文章目录 abstract常见曲线的不同形式小结:一览表分析圆锥曲线的极坐标方程非标准位置的圆锥曲线参数方程应用比较 refs abstract 常见平面曲线的方程的不同表示方式 常见曲线的不同形式 下面以平面曲线为对象讨论参数方程通常是对普通方程的补充和增强,曲线的普通方程(直角…...

element使用小结
1、tabel表头文字自定义效果(换行,不同颜色) 换行: // 方法一 <el-table-columnprop"otherCost":label"本期累计\n(元)"> // 通过:label添加\n </el-table-column>.xx .cell {white-space: pre-…...
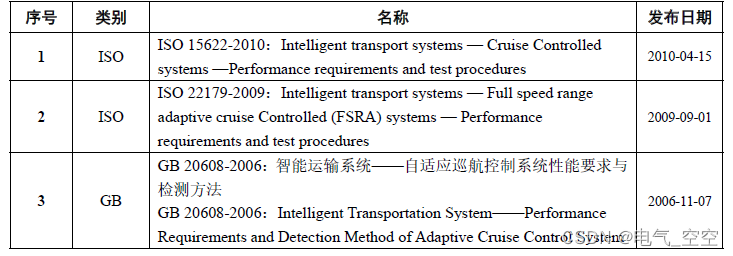
自动驾驶DCLC 功能规范
目录 1 概述Summary....................................................................................................... 4 1.1 目的Purpose....................................................................................................... 4 1.2 范围Ran…...
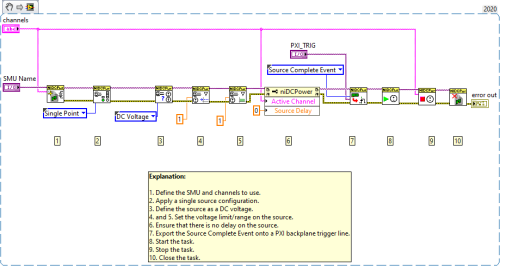
LabVIEW中将SMU信号连接到PXI背板触发线
LabVIEW中将SMU信号连接到PXI背板触发线 本文介绍如何将信号从PXI(e)SMU卡路由到PXI(e)机箱上的背板触发线。该过程涉及使用NI-DCPowerVI将SMU信号导出到PXI_TRIG线上。 在继续操作之前,请确保在开发PC上安装了兼容版…...

[蓝桥杯习题]———位运算、判断二进制1个数
⭐Hello!这里是欧_aita的博客。 ⭐今日语录:行动胜过一切。 ⭐个人主页:欧_aita ψ(._. )>⭐个人专栏: 数据结构与算法(内含蓝桥杯习题) MySQL数据库 位运算 位运算位运算的定义简单运用 实战刷题题目思路代码实现声…...

3DCAT为华东师大设计学院打造元宇宙数字虚拟学院
6月11日,华东师范大学设计学院在chi K11美术馆举办了一场别开生面的 2023 年本科毕业设计暨项目实践教学现场演示展。其中,元宇宙数字虚拟学院(一期)的现场发布会引起了现场震撼,吸引了众多观众的目光和参与。 该元宇宙…...

AIGC 3D即将爆发,混合显示成为产业数字化的生产力平台
2023年,大语言模型与生成式AI浪潮席卷全球,以文字和2D图像生成为代表的AIGC正在全面刷新产业数字化。而容易为市场所忽略的是,3D图像生成正在成为下一个AIGC风口,AIGC 3D宇宙即将爆发。所谓AIGC 3D宇宙,即由文本生成3D…...

时间序列预测实战(二十一)PyTorch实现TCN卷积进行时间序列预测(专为新手编写的自研架构)
一、本文介绍 本篇文章给大家带来的是利用我个人编写的架构进行TCN时间序列卷积进行时间序列建模(专门为了时间序列领域新人编写的架构,简单不同于市面上大家用GPT写的代码),包括结果可视化、支持单元预测、多元预测、模型拟合效…...

探索计算机视觉:深度学习与图像识别的融合
探索计算机视觉:深度学习与图像识别的融合 摘 要: 本文将探讨计算机视觉领域中的深度学习技术,并重点关注图像识别方面的应用。我们将介绍卷积神经网络(CNN)的原理、常用的图像数据集以及图像识别的实际应用场景&…...

屏蔽WordPress评论中长URL地址方法
由于WordPress是比较常见的CMS程序之一,所以很多网络营销推广也会基于WP去群发外链和广告信息。这里,我们可以通过屏蔽特定关键字、屏蔽特定字符的方式,或者是屏蔽评论内容的长短来限制评论。还有一个我们可以通过评论内容的URL地址的长度来屏…...

【教程】 一文部署配置并入门 Redis
综述 什么是Redis Redis官网——Redis.io Redis, 作为一个高性能的键值对数据库,主要应用于以下场景: 缓存系统:由于其高速读写能力,Redis 非常适合用作缓存系统,减少数据库负载。 会话存储(Session St…...

数据被锁住了?如何应对.mkp病毒的攻击
导言: 在数字时代的舞台上,.mkp勒索病毒如幽灵般悄然崭露头角,威胁着无数个体和组织的数据安全。本文将深度挖掘.mkp勒索病毒的狡猾本质,并为你揭示应对感染的独特方法,以及如何巧妙规避这个数字威胁。 如果您在面对被…...

【Shell】Shell基础学习
一、shell脚本 (1)第一个shell脚本 #!/bin/bash #this is a comment echo "hello world"一个shell脚本永远以“#!”开头,这是一个脚本开始的标记,它是告诉系统执行这个文件需要用某个解释器,后面的/bin/bash就是指明解释器的具体位置。 “#”开头是注释 …...

python文件读取
相对路径 读文件 打印txt文件 fopen(".\data.txt","r",encoding"utf-8") contentf.read() print(content) f.close()with open(".\data.txt","r",encoding"utf-8") as f:contentf.read()print(content)contentf…...

第16关 革新云计算:如何利用弹性容器与托管K8S实现极速服务POD扩缩容
------> 课程视频同步分享在今日头条和B站 天下武功,唯快不破! 大家好,我是博哥爱运维。这节课给大家讲下云平台的弹性容器实例怎么结合其托管K8S,使用混合服务架构,带来极致扩缩容快感。 下面是全球主流云平台弹…...

算法通关村第十二关|黄金挑战|最长公共前缀字符串压缩
1.最长公共前缀 原题:力扣14. 1.从前到后比较每个字符串的同一个位置。 public String longestCommonPrefix(String[] strs) {if (strs null || strs.length 0) {return "";}int length strs[0].length();int count strs.length;for (int i 0; i …...
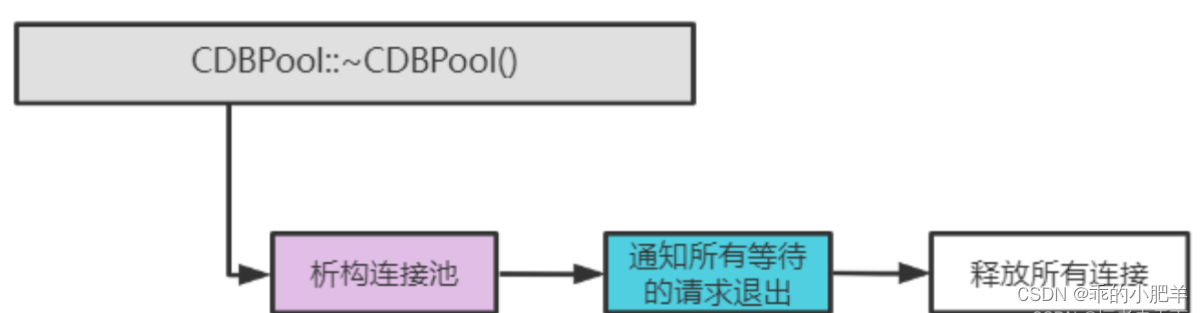
池式组件 ----- Mysql连接池的原理实现
前言 本文是mysql连接池的实现。学完mysql连接池之后,接下来会结合多线程来进行测试,看看使用连接池性能高,还是不要连接池性能高,具体能差多少。当然这是下一篇文章了哈哈哈哈哈。当前首要任务是学会连接池,会都不会…...
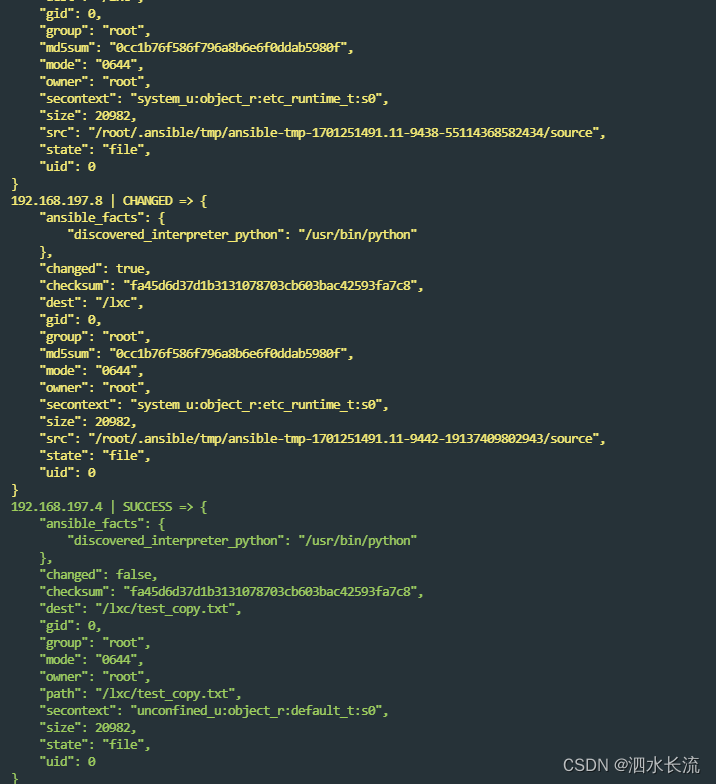
1.自动化运维工具Ansible的安装
1.物料准备 四台服务器,其中一个是主控机,三个为host 2.安装 在主控机上安装ansible 2.1 设置EPEL仓库 Ansible仓库默认不在yum仓库中,因此我们需要使用下面的命令启用epel仓库。 yum install epel-release -y2.2 执行安装命令 yum i…...

[个人笔记] Apache2.4配置TLS1.3安装openssl1.1.1
Linux - 运维篇 第二章 Apache2.4配置TLS1.3&安装openssl1.1.1 Linux - 运维篇系列文章回顾Apache2.4配置TLS1.3&安装openssl1.1.1参考来源 系列文章回顾 第一章 php-fpm编译和使用openssl扩展 Apache2.4配置TLS1.3&安装openssl1.1.1 [rootlocalhost ~]# yum ins…...

解密Kafka主题的分区策略:提升实时数据处理的关键
目录 一、Kafka主题的分区策略概述1.1 什么是Kafka主题的分区策略?1.2 为什么分区策略重要? 二、Kafka默认分区策略2.1 Round-Robin分区策略 三、自定义分区策略3.1 编写自定义分区器3.2 最佳实践:如何选择分区策略 四、分区策略的性能考量4.…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
