时间复杂度为 O(n^2) 的排序算法 | 京东物流技术团队
对于小规模数据,我们可以选用时间复杂度为 O(n2) 的排序算法。因为时间复杂度并不代表实际代码的执行时间,它省去了低阶、系数和常数,仅代表的增长趋势,所以在小规模数据情况下, O(n2) 的排序算法可能会比 O(nlogn) 的排序算法执行效率高。不过随着数据规模增大, O(nlogn) 的排序算法是不二选择。本篇我们主要对 O(n2) 的排序算法进行介绍,在介绍之前,我们先了解一下算法特性:
-
算法特性:
-
稳定性:经排序后,若等值元素之间的相对位置不变则为稳定排序算法,否则为不稳定排序算法
-
原地排序:是否借助额外辅助空间
-
自适应性: 自适应性排序受输入数据的影响,即最佳/平均/最差时间复杂度不等,而非自适应排序时间复杂度恒定
-
本篇我们将着重介绍插入排序,选择排序和冒泡排序了解即可。
插入排序
插入排序的工作方式像整理手中的扑克牌一样,即不断地将每一张牌插入到其他已经有序的牌中适当的位置。
插入排序的当前索引元素左侧的所有元素都是有序的:若当前索引为 i,则 [0, i - 1] 区间内的元素始终有序,这种性质被称为循环不变式,即在第一次迭代、迭代过程中和迭代结束时,这种性质始终保持不变。
不过,这些有序元素的索引位置暂时不能确定,因为它们可能需要为更小的元素腾出空间而向右移动。插入排序的代码实现如下:
private void sort(int[] nums) {for (int i = 1; i < nums.length; i++) {int base = nums[i];int j = i - 1;while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j--];}nums[j + 1] = base;}}它的实现逻辑是取未排序区间中的某个元素为基准数base,将base与其左侧已排序区间元素依次比较大小,并"插入"到正确位置。插入排序对部分有序(数组中每个元素距离它的最终位置都不远或数组中只有几个元素的位置不正确等情况)的数组排序效率很高。事实上,当逆序很少或数据量不大(n2和nlogn比较接近)时,插入排序可能比其他任何排序算法都要快,这也是一些编程语言的内置排序算法在针对小数据量数据排序时选择使用插入排序的原因。
算法特性:
-
空间复杂度:O(1)
-
原地排序
-
稳定排序
-
自适应排序:当数组为升序时,时间复杂度为 O(n);当数组为降序时,时间复杂度为 O(n2)
希尔排序
插入排序对于大规模乱序数组排序很慢,因为它只会交换相邻的元素,所以元素只能一步步地从一端移动到另一端,如果最小的元素恰好在数组的最右端,要将它移动到正确的位置需要移动 N - 1 次。
希尔排序是基于插入排序改进的排序算法,它可以交换不相邻的元素以对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。它的思想是使数组中间隔为 h 的元素有序(h 有序数组),如下图为间隔为 4 的有序数组:
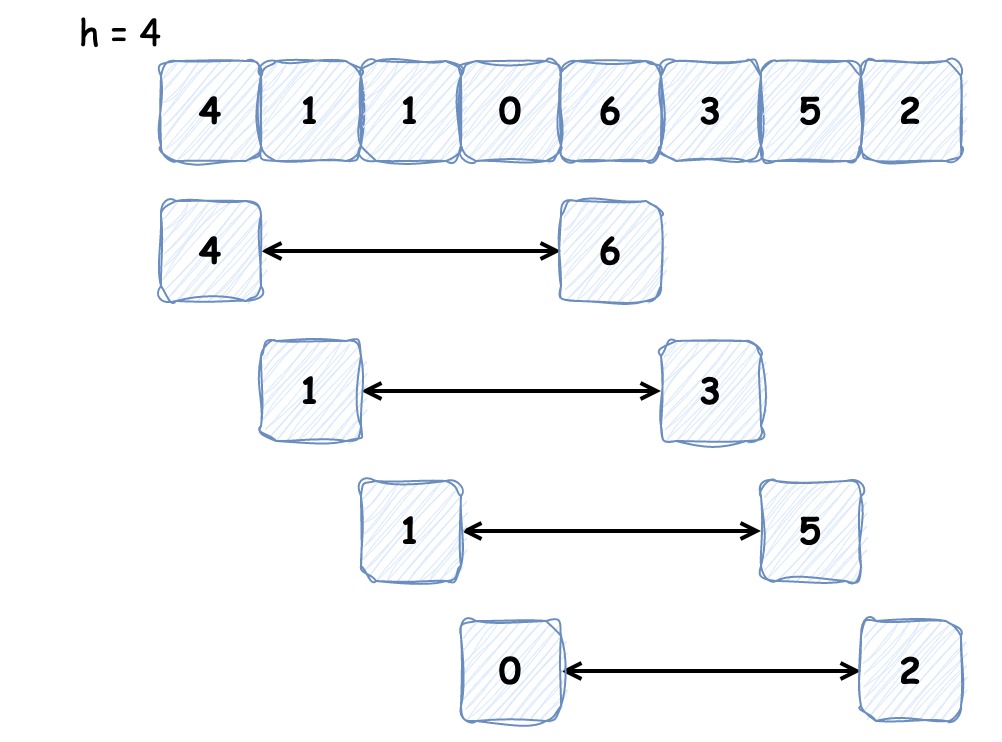
排序之初 h 较大,这样我们能将较小的元素尽可能移动到靠近左端的位置,为实现更小的 h 有序创造便利,最后一次循环时 h 为 1,便是我们熟悉的插入排序。这就是希尔排序的过程,代码实现如下:
private void sort(int[] nums) {int N = nums.length;int h = 1;while (h < N / 3) {h = 3 * h + 1;}while (h >= 1) {for (int i = h; i < N; i++) {int base = nums[i];int j = i - h;while (j >= 0 && nums[j] > base) {nums[j + h] = nums[j];j -= h;}nums[j + h] = base;}h /= 3;}}希尔排序更高效的原因是它权衡了子数组的规模和有序性,它也可以用于大型数组。排序之初,各个子数组都很短,排序之后子数组都是部分有序的,这两种情况都很适合插入排序。
选择排序
选择排序的实现非常简单:每次选择未排序数组中的最小值,将其放到已排序区间的末尾,代码实现如下:
private void sort(int[] nums) {for (int i = 0; i < nums.length; i++) {int min = i;for (int j = i + 1; j < nums.length; j++) {if (nums[j] < nums[min]) {min = j;}}swap(nums, i, min);}}private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}算法特性:
-
空间复杂度:O(1)
-
原地排序
-
非稳定排序:会改变等值元素之间的相对位置
-
非自适应排序:最好/平均/最坏时间复杂度均为 O(n2)
冒泡排序
冒泡排序通过连续地比较与交换相邻元素实现排序,每轮循环会将未被排序区间内的最大值移动到数组的最右端,这个过程就像是气泡从底部升到顶部一样,代码实现如下:
public void sort(int[] nums) {for (int i = nums.length - 1; i > 0; i--) {// 没有发生元素交换的标志位boolean flag = true;for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {swap(nums, j, j + 1);flag = false;}}if (flag) {break;}}}private void swap(int[] nums, int i, int j) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}算法特性:
-
空间复杂度:O(1)
-
原地排序
-
稳定排序
-
自适应排序:经过优化后最佳时间复杂度为 O(n)
巨人的肩膀
-
《算法导论 第三版》第 2.1 章
-
《算法 第四版》第 2.1 章
-
《Hello 算法》第 11 章
-
排序算法-希尔排序
作者:京东物流 王奕龙
来源:京东云开发者社区 自猿其说Tech 转载请注明来源
相关文章:

时间复杂度为 O(n^2) 的排序算法 | 京东物流技术团队
对于小规模数据,我们可以选用时间复杂度为 O(n2) 的排序算法。因为时间复杂度并不代表实际代码的执行时间,它省去了低阶、系数和常数,仅代表的增长趋势,所以在小规模数据情况下, O(n2) 的排序算法可能会比 O(nlogn) 的…...
关于前端学习的思考-内边距、边框和外边距
从最简单的盒子开始思考 先把实际应用摆出来: margin:居中,控制边距。 padding:控制边距。 border:制作三角形。 盒子分为内容盒子,内边距盒子,边框和外边距。 如果想让块级元素居中&#…...

【linux】/etc/security/limits.conf配置文件详解、为什么限制、常见限制查看操作
文章目录 一. limits.conf常见配置项详解二. 文件描述符(file descriptor)简述三. 为什么限制四. 相关操作1. 展示当前资源限制2. 查看系统当前打开的文件描述符数量3. 查看某个进程打开的文件描述符数量4. 各进程占用的文件描述符 /etc/security/limits…...
Windows系统下更新后自带的画图软件出现马赛克bug
一.bug的样子🍗 在使用橡皮后,原来写的内容会变成马赛克。而我们希望它是纯白色的。 二.解决方法🍗 第一步 第二步 第三步 三. 解决后的效果🍗 用橡皮擦随便擦都不会出现马赛克了。 更新过后,想用win自带的画图软件会出…...

[HTML]Web前端开发技术6(HTML5、CSS3、JavaScript )DIV与SPAN,盒模型,Overflow——喵喵画网页
希望你开心,希望你健康,希望你幸福,希望你点赞! 最后的最后,关注喵,关注喵,关注喵,佬佬会看到更多有趣的博客哦!!! 喵喵喵,你对我真的…...

SQL练习
建数据库: mysql> create database worker; Query OK, 1 row affected (0.00 sec) mysql> CREATE TABLE worker (-> 部门号 int(11) NOT NULL,-> 职工号 int(11) NOT NULL,-> 工作时间 date NOT NULL,-> 工资 float(8,2) NOT NULL,-> 政治面貌…...
创始人于东来:胖东来员工不想上班,请假不允许不批假!
12月2日早晨,一则关于“胖东来员工不想上班请假不允许不批假”的新闻登上了热搜,引起了广泛关注。熟悉胖东来的网友们可能知道,这并不是这家企业第一次成为热搜的焦点。据白鹿视频12月1日报道,11月25日,河南许昌的胖东…...
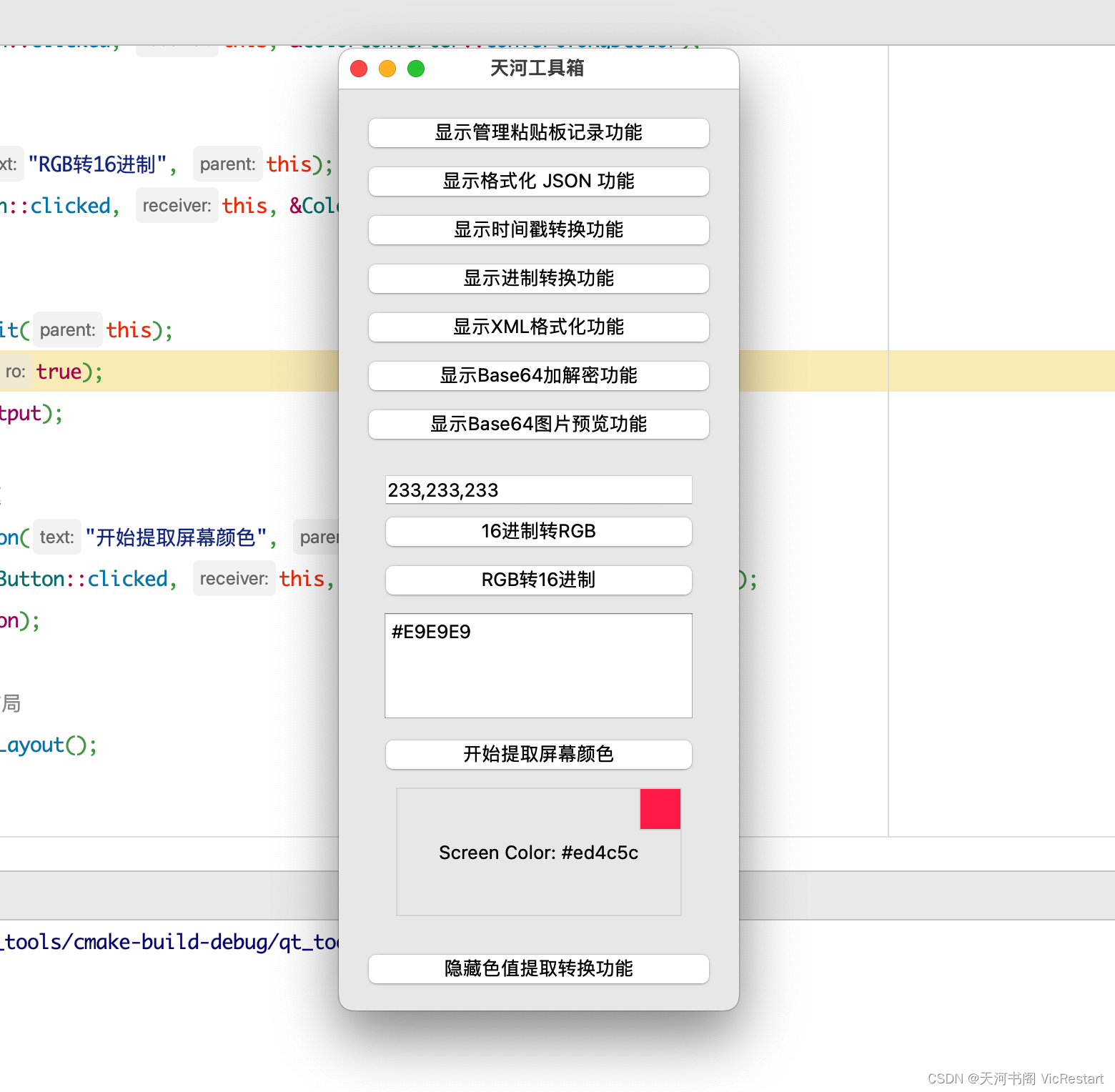
C++学习之路(十五)C++ 用Qt5实现一个工具箱(增加16进制颜色码转换和屏幕颜色提取功能)- 示例代码拆分讲解
上篇文章,我们用 Qt5 实现了在小工具箱中添加了《Base64图片编码预览功能》功能。为了继续丰富我们的工具箱,今天我们就再增加两个平时经常用到的功能吧,就是「 16进制颜色码转RGB文本 」和 「屏幕颜色提取」功能。下面我们就来看看如何来规划…...
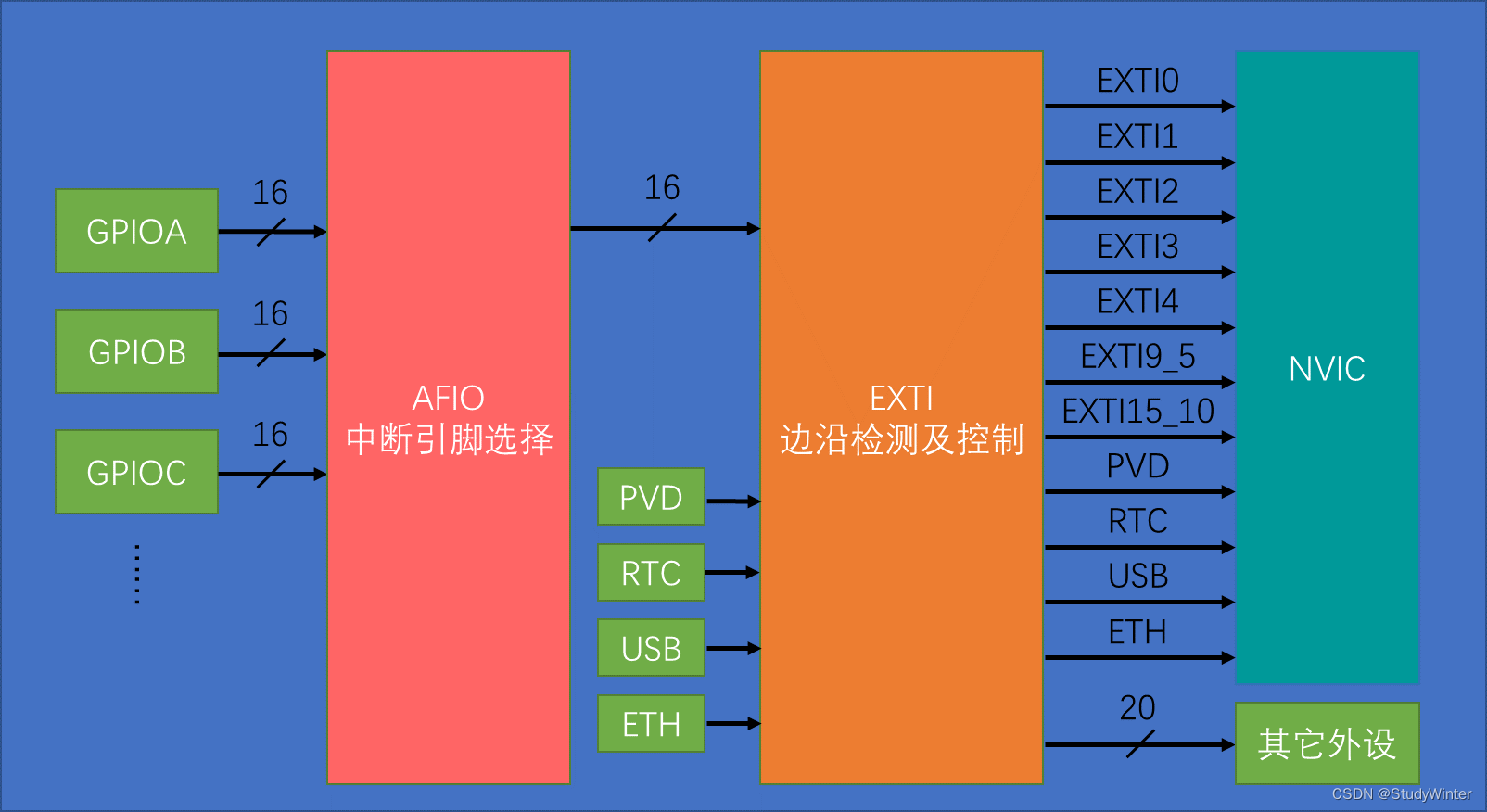
【STM32】EXTI外部中断
1 中断系统 1.1 中断简介 中断:在主程序运行过程中,出现了特定的中断触发条件(中断源),使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继续运行。 比如&a…...
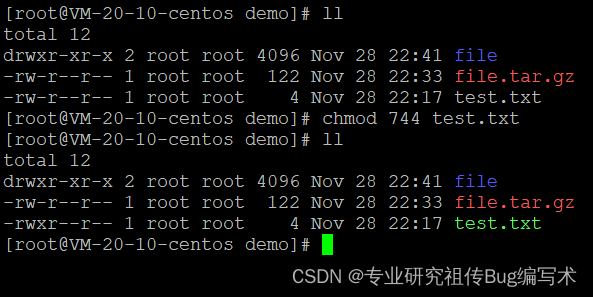
Linux系统的常见命令十三,显示系统进程状态、文件权限、修改文件或目录所有者和所属组命令(ps、chmod和chown)
本文主要介绍Linux系统的显示系统进程状态、文件权限、修改文件或目录所有者和所属组命令,(ps、chmod和chown) 目录 显示系统进程状态文件权限设置(chmod)修改文件或目录所有者和所属组(chown) …...

Python 批量修改文件名
主要步骤 通过os.listdir查看该文件夹下所有的文件(包括文件夹)遍历所有文件,如果是文件夹则跳过,或指定跳过指定文件获取文件扩展名按照需求生成新的文件路径文件名进行重命名 代码示例 # -*- coding: utf-8 -*- import osdef…...

git的基本命令操作超详细解析教程
Git基础教学 1、初始化配置2、初始化仓库3、工作区域和文件状态4、添加和提交文件5、git reset 回退版本6、git diff查看差异7、删除文件git rm8、.gitignore9、本地文件提交到远程仓库10、分支基础 Git:一个开源的分布式版本控制系统,它可以在本地和远程…...
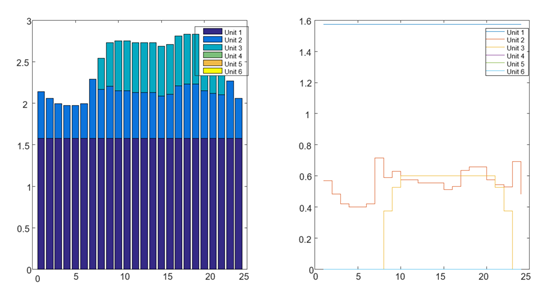
【代码】两阶段鲁棒优化/微电网经济调度入门到编程
内容包括 matlab-yalmipcplex微电网两阶段鲁棒经济调度(刘) matlab-yalmipcplex两阶段鲁棒微电网容量经济优化调度 两阶段鲁棒优化CCG列于约束生成和Benders代码,可扩展改编,复现自原外文论文 【赠送】虚拟储能单元电动汽车建…...
(私人复习资料))
【图论】重庆大学图论与应用课程期末复习资料2-各章考点(填空证明部分)(私人复习资料)
图论各章考点 一、图与网络的基本概念二、树三、连通性四、路径算法五、匹配六、行遍性问题七、平面图 一、图与网络的基本概念 生成子图:生成子图 G ’ G’ G’中顶点个数V’必须和原图G中V的数量相同,而 E ’ ∈ E E’∈E E’∈E即可。顶点集导出子图…...

基于Intel® AI Analytics Toolkits的智能视频监控系统
【oneAPI DevSummit & OpenVINODevCon联合黑客松】 跳转链接:https://marketing.csdn.net/p/d2322260c8d99ae24795f727e70e4d3d 目录 1方案背景 2方案描述 3需求分析 4技术可行性分析 5详细设计5.1数据采集 5.2视频解码与帧提取 5.3人脸检测 5.4行为识别…...

深度学习中的注意力机制:原理、应用与实践
深度学习中的注意力机制:原理、应用与实践 摘要: 本文将深入探讨深度学习中的注意力机制,包括其原理、应用领域和实践方法。我们将通过详细的解析和代码示例,帮助读者更好地理解和应用注意力机制,从而提升深度学习模…...

将本地项目推送到github
欢迎大家到我的博客浏览。将本地项目推送到github | YinKais Blog 本地项目上传至 GitHub<!--more--> 1、进入项目根目录,初始化本地仓库 git init 2、创建密钥:创建 .ssh 文件夹,并进入 .ssh 文件夹 mkdir .ssh cd .ssh/ 3、生成…...

[读论文]meshGPT
概述 任务:无条件生成mesh (无颜色)数据集:shapenet v2方法:先trian一个auto encoder,用来获得code book;然后trian一个自回归的transformermesh表达:face序列。face按规定的顺序&a…...

反序列化漏洞详解(一)
目录 一、php面向对象 二、类 2.1 类的定义 2.2 类的修饰符介绍 三、序列化 3.1 序列化的作用 3.2 序列化之后的表达方式/格式 ① 简单序列化 ② 数组序列化 ③ 对象序列化 ④ 私有修饰符序列化 ⑤ 保护修饰符序列化 ⑥ 成员属性调用对象 序列化 四、反序列化 …...

键盘打字盲打练习系列之指法练习——2
一.欢迎来到我的酒馆 盲打,指法练习! 目录 一.欢迎来到我的酒馆二.开始练习 二.开始练习 前面一个章节简单地介绍了基准键位、字母键位和数字符号键位指法,在这个章节详细介绍指法。有了前面的章节的基础练习,相信大家对盲打也有了…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
