Leetcode DAY 49~50:买卖股票的最佳时机 1 2 3 4
- 121. 买卖股票的最佳时机
1、贪心算法
class Solution {
public:int maxProfit(vector<int>& prices) {//贪心int low = INT_MAX;int res = 0;for(int i = 0; i < prices.size(); i++) {low = min(low, prices[i]); //左最小价格res = max(res, prices[i] - low); //当前-左最小的max}return res;}
};2、动态规划
dp[i][0]表示第i天持有股票最大现金 -> max(前一天持有股票的最大现金, 前一天买入股票的现金)
dp[i][1]表示第i天不持有股票最大现金 -> max(前一天不持有股票最大现金, 前一天持有第i天买入的现金)
class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(),vector<int>(2, 0));dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < prices.size(); i++){dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[prices.size() - 1][1];}
};122.买卖股票的最佳时机II
1、dp
dp[i][0]表示第i天持有股票时的所的现金
dp[i][1]表示第i天不持有股票所得的现金
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2,0));dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[n - 1][1];}
};2、其他
class Solution:def maxProfit(self, prices: List[int]) -> int:res = 0for i in range(1, len(prices)):if prices[i] - prices[i - 1] > 0:res += prices[i] - prices[i - 1]return res- 123.买卖股票的最佳时机III
!最多可以完成两笔交易!
1、递推公式
dp[i][0] 第一次持有的现金 <--- dp[i - 1][0] - prices[i]
dp[i][1] 第一次不持有的现金 <--- dp[i - 1][1] dp[i - 1][0] + prices[i]
dp[i][2] 第二次持有的现金 <--- dp[i - 1][2] dp[i - 1][1] - prices[i]
dp[i][3] 第二次不持有的现金 <--- dp[i - 1][3] dp[i - 1][2] + prices[i]
2、初始化
dp[0][0] = -prices[0]
dp[0][1] = 0
dp[0][2] = -prices[0]
dp[0][3] = 0
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();if(n == 0)return 0;vector<vector<int>> dp(n, vector<int>(4, 0));dp[0][0] = -prices[0];dp[0][2] = -prices[0];for(int i = 1; i < n; i++) {dp[i][0] = max(dp[i - 1][0], -prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] - prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] + prices[i]);}return dp[n - 1][3];}
};- 188.买卖股票的最佳时机IV
通过上一题 类比得到
class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2 * k + 1, 0));for(int i = 1; i <= 2*k; i += 2){dp[0][i] = - prices[0];}for(int i = 1; i < n; i++) {for(int j = 1; j <= 2 * k; j++) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] + (1 - 2 * (j % 2)) * prices[i]);//1 - 2 * (j % 2)用来区分 奇数和偶数}}return dp[n - 1][2 *k];}
};相关文章:

Leetcode DAY 49~50:买卖股票的最佳时机 1 2 3 4
121. 买卖股票的最佳时机 1、贪心算法 class Solution { public:int maxProfit(vector<int>& prices) {//贪心int low INT_MAX;int res 0;for(int i 0; i < prices.size(); i) {low min(low, prices[i]); //左最小价格res max(res, prices[i] - low); //当前…...
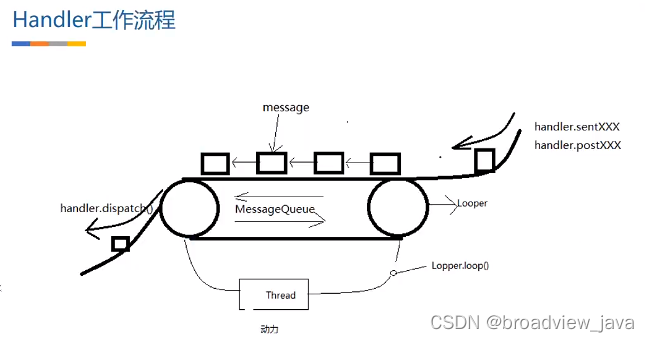
Android Handler机制(二) Handler 实现原理
一. 前言 接上一篇文章为什么设计Handler , 我们来继续讲解一下Handler的实现原理, 俗话说一个好汉三个帮, 接下来一步一步引入各个主角,并说明它们在Handler机制中扮演的角色和作用. 二. Handler实现原理 首先我们先确定一个结论: 使用 Handler 是希望它被实例化在哪个线程&a…...
 详解mapping之keyword)
Elasticsearch教程(19) 详解mapping之keyword
Elasticsearch已升级,新版Elasticsearch keyword博客参考下面这篇【Elasticsearch教程8】Mapping字段类型之keyword_elasticsearch的keyword_亚瑟弹琴的博客-CSDN博客 1 前言 本文基于ES7.6,如果是之前版本,是有区别的。 ES支持的字段类型很…...
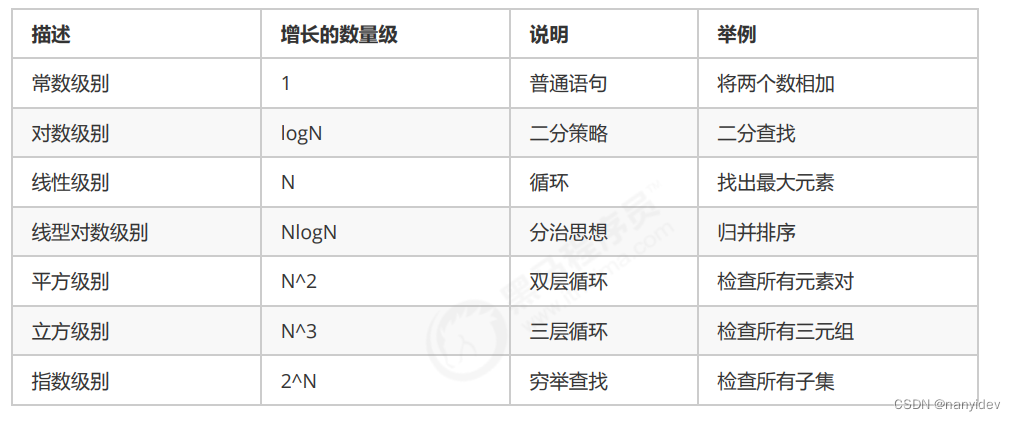
LeetCode算法复杂度分析(时间复杂度空间复杂度)
文章目录前言时间复杂度1.概述2.大O记法3.常见类型空间复杂度1.概述2.常见类型典型算法的复杂度分析1.递归算法2.哈希表前言 我们知道,研究算法的最终目的就是如何花更少的时间,如何占用更少的内存去完成相同的需求。 时间复杂度 1.概述 我们要计算算…...
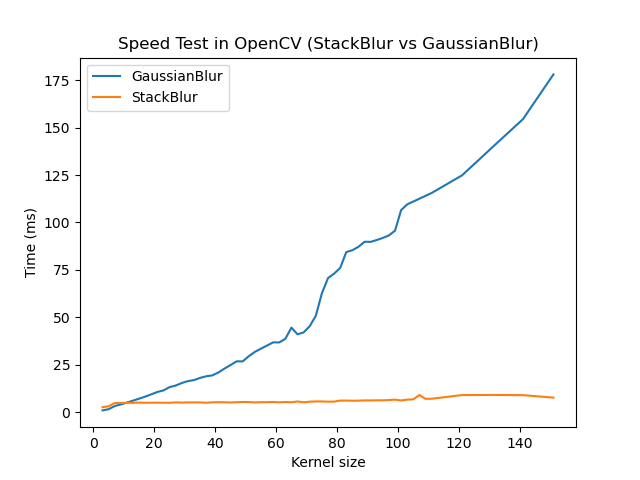
Android OpenCV(七十三):吊打高斯模糊的StackBlur Android 实践
前言 OpenCV 4.7.0 2022年12月28日Release,ChangeLog中提到 Stackblur algorithm implementation. Stackblur是一种高斯模糊的快速近似,由Mario Klingemann发明。其计算耗时不会随着kernel size的增大而增加,专为大kernel size的模糊滤波场景量身定制。 使用建议:当kerne…...

4.排序算法之一:冒泡排序
排序算法稳定性假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]r[j],且r[i]在r[j]之前,而在排序后的序列中,r[…...

python自学之《21天学通Python》(16)——第19章 用Pillow库处理图片
Pillow是Python2.X时代比较流行的Python ImagingLibrary(简称Pillow)图像处理库的分支,并修复了一些bug。Pillow提供了对Python3的支持,为Python3解释器提供了图像处理的功能。和Pillow库一样提供了广泛的文件格式支持、高效的内部…...
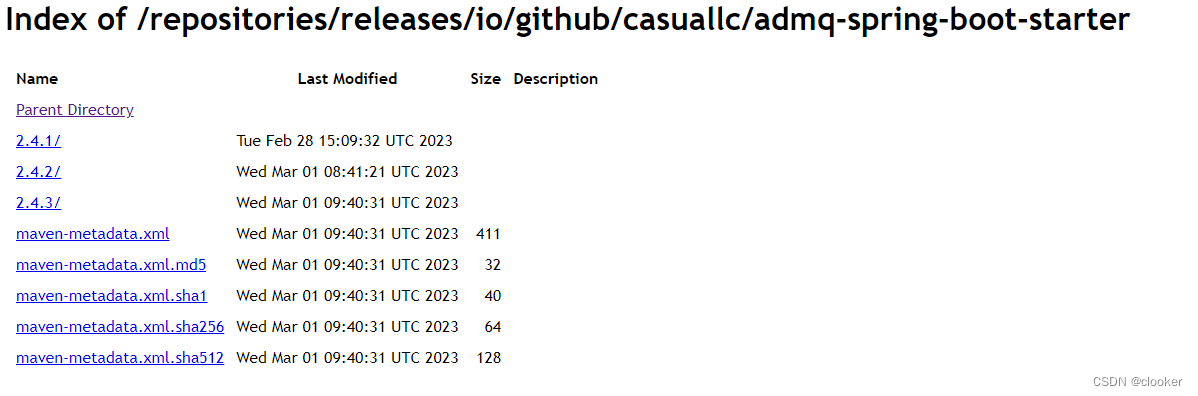
发布依赖到maven仓库
maven中央仓库是一个开放的仓库,所以我们也可以把自己开发的jar推送到远程仓库,这样可以直接引入pom依赖使用我们的库。 准备工作 ● 需要一个github账号(程序员必备) ● 网络代理(涉及到的网站通常没版本在国内直接访…...
Laravel-admin之自定义操作日志
laravel-admin是封装性极好的框架,自带的就有操作日志的记录,但是对于非开发人员可能看不懂这个日志,所以就想着给修改一下,以谁修改了什么,谁删除了什么,谁审核了什么,谁添加了什么类似&#x…...

用Python做了一个法律查询小工具,非常好用
用Python做了一个法律查询小工具,非常好用效果展示准备工作不会的话可以点我直达代码和视频讲解,我都准备好了主要代码哈喽兄弟,今天给大家分享一个Python tkinter制作法律查询小工具。 光爬虫大家也只能自己用用,就算打包了exe&…...
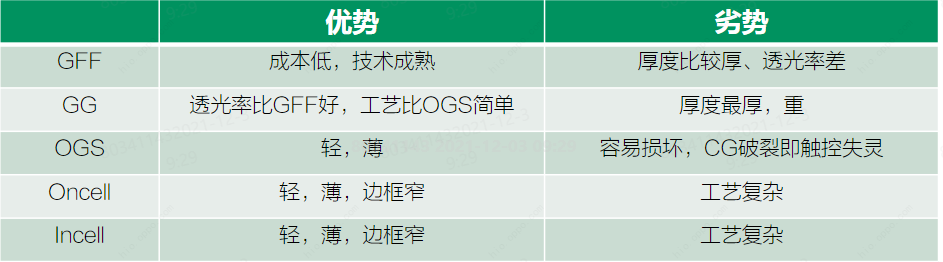
工作篇:触摸屏原理介绍
一、触摸屏概述 触摸屏作为一种新的输入设备,它是目前最简单、方便、自然的一种人机交互方式。 当接触了屏幕上的图形按钮时,屏幕上的触觉反馈系统可根据预先编程的程式驱动各种连结装置,可用以取代机械式的按钮面板,并借由液晶…...
Ep_操作系统面试题-操作系统的分类
答案 单体系统 整个操作系统是以程序集合来编写的,链接在一块形成一个二进制可执行程序,这种系统称为单体系统。 分层系统 每一层都使用下面的层来执行其功能。 微内核 微内核架构的内核只保留最基本的能力,把一些应用放到了用户空间 客户-…...

iframe或document监听滚动事件不起作用
有时候我们会遇到监听iframe或document的滚动事件不起作用的情况,在排除代码写错的情况下,我们应该考虑此时的document是否可以滑动。 1、为什么document不能监听滑动? 就很奇怪,明明页面时有滚动条的,为什么说document不可滑动…...
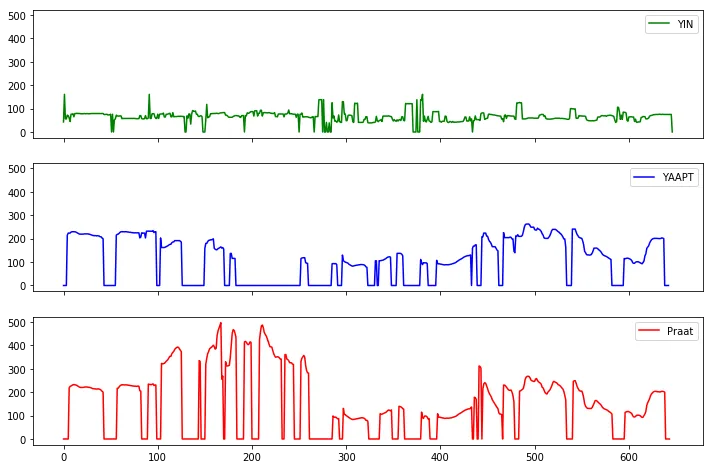
基频估计算法简介
基频估计算法 F0 estimate methods 估计F0的方法可以分为三类:基于时域、基于频域、或混合方法。本文详细介绍了这些方法。 所有的算法都包含如下三个主要步骤: 1.预处理:滤波,加窗分帧等 2.搜寻:可能的基频值F0(候选…...

linux修改DNS 系统版本Kylin V10桌面版
配置DNS在银河麒麟桌面操作系统V10 SP1 中修改DNS信息,直接修改/etc/resolv.conf文件中的DNS信息,不能生效。应该参考如下步骤:一、首先修改 /etc/systemd/resolved.conf文件,在其中添加DNS信息在终端中执行以下命令:s…...

如何使用 AWS Lambda 运行 selenium
借助 AWS Lambda 运行 selenium 来爬取网络数据。 简介 与手动从网站收集数据相比,爬虫可以为我们节省很多时间,对于爬虫的每次请求而言,这相当于 AWS Lambda 的每次函数的运行。 AWS Lambda 是一种将脚本部署到云的简单且价格低廉的服务&…...
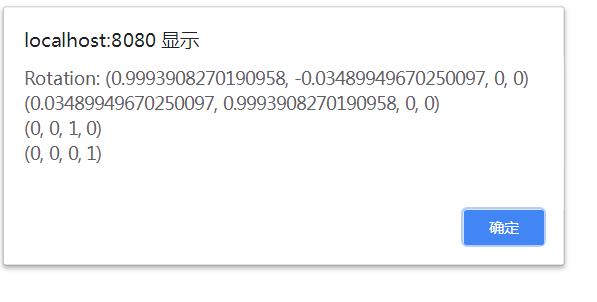
认识Cesium旋转大小变量
前文代码中有如下;矩阵乘以旋转大小,还放入mat; Cesium.Matrix4.multiply(mat, rotationX, mat); 初看以为rotationX是一个数值,因为矩阵可以和数相乘; 但是看它的代码,rotationX是由一长串代码获得的&a…...

异响加持、吐槽声不断,小鹏G9难解困局
小鹏汽车的烦恼就好比红尘中的三千青丝,小鹏G9“惊魂48小时”的恐慌还未平息,车门异响等问题就已经层出不穷,再次将小鹏汽车推上风口浪尖。 可以毫不客气的说,G9承载着小鹏汽车盈利的希望,但在原本处于上升之势的G9却…...

【react】react18的学习
一、安装 $ create-react-app [Project name]默认支持sass 二、核心依赖 react:react 核心 react-dom:用于开发渲染web 应用; react-scripts:封装webpack服务; "start": "react-scripts start&quo…...

Ep_操作系统面试题-什么是线程,线程和进程的区别
1. 一个进程中可以有多个线程,多个线程共享进程的堆和方法区 (JDK1.8 之后的元空间),但是每个线程有自己的程序计数器、虚拟机栈和 本地方法栈。 2.进程是资源分配的最小单位,线程是CPU调度的最小单位 视频讲解: https://edu.csdn.net/course/detail/38090 点我…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
