【C语言】函数递归详解(一)
目录
1.什么是递归:
1.1递归的思想:
1.2递归的限制条件:
2.递归举例:
2.1举例1:求n的阶乘:
2.1.1 分析和代码实现:
2.1.2图示递归过程:
2.2举例2:顺序打印一个整数的每一位:
2.2.1分析和代码实现:
2.2.2图示递归过程:
1.什么是递归:
❓递归是学习C语言函数绕不开的一个话题,那什么是递归呢
⭐递归其实是一种解决问题的方法,在C语言中,递归就是函数自己调用自己。
写一个简单的C语言递归代码:
#include<stdio.h>
int main()
{printf("hehe\n");mian();return 0;
}上述就是一个简单的递归程序,只不过上面的递归只是为了演示递归的基本形式,不是为了解决问题,代码最终会陷入死递归,导致栈溢出(Stack overflow)。

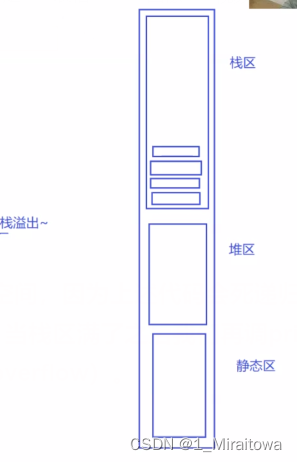
栈溢出的原因:
⭐我们每次调用printf()函数时都会在栈区开辟一块空间,因为上述代码会死递归,所以会一直调用printf()函数,但是栈区的空间是有限的,当栈区满了之后我们再调printf()函数时,系统想继续分配空间此时就会栈溢出(Stack overflow)。
1.1递归的思想:
把一个大型复杂的问题层层转化为一个与原问题相似,但规模较小的子问题来求解;直到子问题不能再被拆分,递归就结束了。所以递归过程就是把大事化小的过程
递归中的递就是递推的意思,归就是回归的意思,接下来慢慢体会 。
1.2递归的限制条件:
递归在书写的时候,有2个必要条件:
1.递归存在限制条件,当满足这个限制条件时,递归便不再继续。
2.每次递归调用之后越来越接近这个限制条件。(渐渐停下来)
在下面的例子中,我们会逐步体会这两个限制条件
2.递归举例:
2.1举例1:求n的阶乘:
阶乘(factorial):一个正整数的阶乘是所有小于等于该数的正整数的积,且0的阶乘为1,
自然数n的阶乘写作n!
2.1.1 分析和代码实现:
以5!为例子我们进行分析
5!=5*4*3*2*1 = 5*4!
4!= 4*3*2*1 = 4*3!
3!= 3*2*1 = 3*2!
2!= 2*1 = 2*1!
1!= 1 = 1*0!
0!=1
通过观察5!我们可以发现当n>0时,n!=n*(n-1)!,当n=0时,n!=1。
如下图所示:

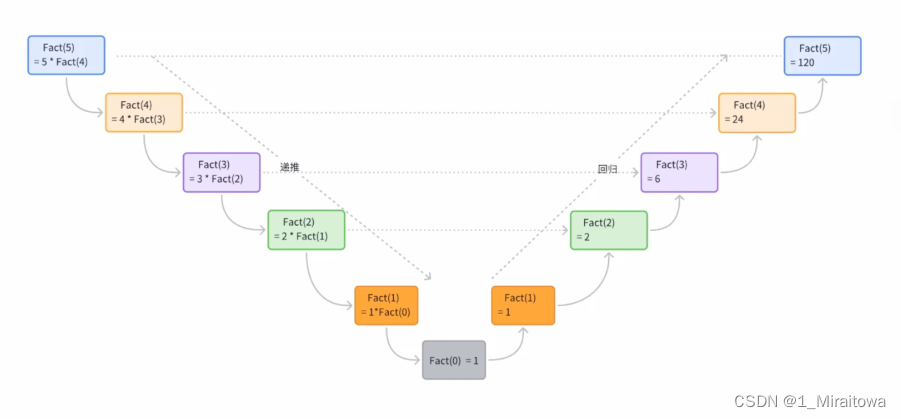
因此我们可以定义求n!函数为Fact(n),当n>0时,Fact(n)=n*Fact(n-1),当n=0时,Fact(n)=1。
代码实现如下:
#include<stdio.h>
int Fact(int n)
{if (n > 0) {return n * Fact(n - 1);}else{return 1;}
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fact(n);printf("%d", ret);
}运行结果如下:

2.1.2图示递归过程:
2.2举例2:顺序打印一个整数的每一位:
输入一个整数m,按照顺序打印整数的每一位
例如:
输入:1234 输出:1 2 3 4
输入:520 输出:5 2 0
2.2.1分析和代码实现:
这个题目,放在我们面前,首先想到的是,怎么得到这个数的每一位呢?
如果n是一位数,那么取出的数字就是它本身,如果n超过一位数(即n>9),就需要拆分每一位。
例如1234:
1234%10得到4,1234/10得到123,相当于去掉了4,继续对123%10得到3,123/10得到12,以此类推,不断重复%10和/ 10的操作,直到1234的每一位都得到;但是我们按照此方法得到的不是1 2 3 4而是倒着的4 3 2 1.
那么我们可以这么想,每一个数字的最低位置是最容易得到的,通过%10就可以得到
我们设想写一个函数Print()来打印n的每一位,如下表示:
Print(n)
如果n是1234,则表示为
Print(1234)//打印1234的每一位
其中1234中的4可以通过%10得到
那么Print(1234)可以分为两步:
1.Print(1234/10)//相当于Print(123)打印123的每一位
2.printf(1234%10)//打印4
完成了上述两个步骤就完成了1234的每一位打印
那么Print(123)又可以拆分为Print(123/10)+printf(123%10)
以此类推下去就有:

直到被打印的数字变成一位数的时候,就不再需要拆分,递归完成,有了上述的分析,代码可以清晰的写出,如下所示:
#include<stdio.h>
void Print(int n)
{if(n>9){Print(n / 10);printf("%d ", n % 10);}else{printf("%d ", n);}
}
int main()
{int n = 0;scanf_s("%d", &n);Print(n);
}运行结果如下:

2.2.2图示递归过程:

以上便是我为大家带来的函数递归的第一部分内容,若有不足,望各位大佬在评论区指出,谢谢大家!可以留下你们点赞、收藏和关注,这是对我极大的鼓励,我也会更加努力创作更优质的作品。再次感谢大家!

相关文章:

【C语言】函数递归详解(一)
目录 1.什么是递归: 1.1递归的思想: 1.2递归的限制条件: 2.递归举例: 2.1举例1:求n的阶乘: 2.1.1 分析和代码实现: 2.1.2图示递归过程: 2.2举例2:顺序打印一个整数的…...

WT588F02B-8S语音芯片助力破壁机:智能声音播放提示IC引领健康生活新潮流
在追求健康饮食的时代潮流中,破壁机作为榨汁、搅拌的重要厨房电器,融入智能技术的趋势不断加强。唯创知音的WT588F02B-8S语音芯片作为声音播放提示IC,为破壁机注入了更智能、便捷的声音提示功能,引领用户迈入健康生活的新潮流。 …...

NXP iMX8M Plus Qt5 双屏显示
By Toradex胡珊逢 简介 双屏显示在显示设备中有着广泛的应用,可以面向不同群体展示特定内容。文章接下来将使用 Verdin iMX8M Plus 的 Arm 计算机模块演示如何方便地在 Toradex 的 Linux BSP 上实现在两个屏幕上显示独立的 Qt 应用。 硬件介绍 Verdin iMX8M Plu…...

RepidJson中Writer类、FilewriteStream类、 PrettyWriter类的区别
rapidjson是一个C的JSON解析库,可以用于解析和序列化JSON数据。 Writer是rapidjson中一种基本的输出流,用于将JSON数据输出到字符串或文件中。 FileWriteStream是一个Writer的子类,它专门用于将JSON数据输出到文件中。相比于普通的Writer&a…...

IntelliJ idea卡顿解决,我遇到的比较管用的方案
Setttings> Build, Execution,Deployment>Debugger> Data Views> Java 取消 Enable "toString()" object view; Speed up debugging in IntelliJ Yesterday, I observed painfully slow debugging in IntelliJ. Every step over or step in took almost…...

Fabric.js 实战开发使用介绍
原生canvas用的多的有哪些槽点就不用我多说了;fabric 作为一个canvas库,提供了非常高效、直观的API操作,使我们对涉及canvas相关的功能开发效率大幅提升~~~~ 简单记录下自己的心得;以下是对比canvas来说的优势: 1.简…...

Vue.directive
Vue.directive( id, [definition] ) 参数: {string} id {Function | Object} [definition] // 注册一个全局自定义指令 v-focus Vue.directive(focus, {// 当被绑定的元素插入到 DOM 中时……inserted: function (el) {// 聚焦元素el.focus()} }) Vue.directive(my…...

webpack优化打包速度
webpack打包速度太慢 优化 1.多线程打包 js压缩和loader 2.优化启动速度 hard-source-webpack-plugin 3.删除无用的 分析类插件 4.DllPlugin通道打包 1.webpack多线程打包 loader loader 使用 thread-loader 将他放置你要使用的loader前面就行,不过这个lorder例如s…...
ALTERNET STUDIO 9.1 Crack
ALTERNET STUDIO 9.1 发布 宣布 AlterNET Studio 9.1 版本今天上线。AlterNET Studio 9.0 是一个中期更新,重点是改进我们所有的组件库。 以下是 AlterNET Studio 9.1 的发布亮点: Roslyn C# 和 Visual Basic 解析器现在支持代码修复/代码重构。 代码修复…...
基于Java技术的选课管理系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

在UBUNTU上使用Qemu和systemd-nspawn搭建RISC-V轻量级用户模式开发环境
参考链接 使用Qemu和systemd-nspawn搭建RISC-V轻量级用户模式开发环境 - 知乎 安装Qemu sudo apt updatesudo apt -y install qemu-user-binfmt qemu-user-static systemd-container sudo apt -y install zstd 配置环境 RISCV_FILEarchriscv-2023-10-09.tar.zstwget -c ht…...
JAVA使用POI向doc加入图片
JAVA使用POI向doc加入图片 前言 刚来一个需求需要导出一个word文档,文档内是系统某个界面的各种数据图表,以图片的方式插入后导出。一番查阅资料于是乎着手开始编写简化demo,有关参考poi的文档查阅 Apache POI Word(docx) 入门示例教程 网上大多数是XXX…...

反向传播算法
反向传播算法的数学解释 反向传播算法是深度学习中用于训练神经网络的核心算法。它通过计算损失函数相对于网络权重的梯度来更新权重,从而最小化损失。 反向传播的基本原理 反向传播算法基于链式法则,它按层反向传递误差,从输出层开始&…...

记录 | ubuntu降低内核版本的方法
降低 ubuntu 内核,比如降低到 4.15 版本,下载对应 4.15.0.128 内核离线安装,网址: http://archive.ubuntu.com/ubuntu/pool/main/l/linux/, 根据实际选择下载,我这里选择,安装的话采用 dpkg -i …...

MX6ULL学习笔记 (八) platform 设备驱动实验
前言: 什么是 Linux 下的 platform 设备驱动 Linux下的字符设备驱动一般都比较简单,只是对IO进行简单的读写操作。但是I2C、SPI、LCD、USB等外设的驱动就比较复杂了,需要考虑到驱动的可重用性,以避免内核中存在大量重复代码&…...

初识Linux:权限(2)
目录 权限 用户(角色) 文件权限属性 文件的权限属性: 有无权限的区别: 身份匹配: 拥有者、所属组的修改: 八进制的转化: 文件的类型: x可执行权限为什么不能执行…...

测试环境使用问题及其优化对策实践
1 背景及问题 G.J.Myers在<软件测试技巧>中提出:测试是为了寻找错误而运行程序的过程,一个好的测试用例是指很可能找到迄今为止尚未发现的错误的测试, 一个成功的测试是揭示了迄今为止尚未发现的错误的测试。 对于新手来说࿰…...
【力扣】206.反转链表
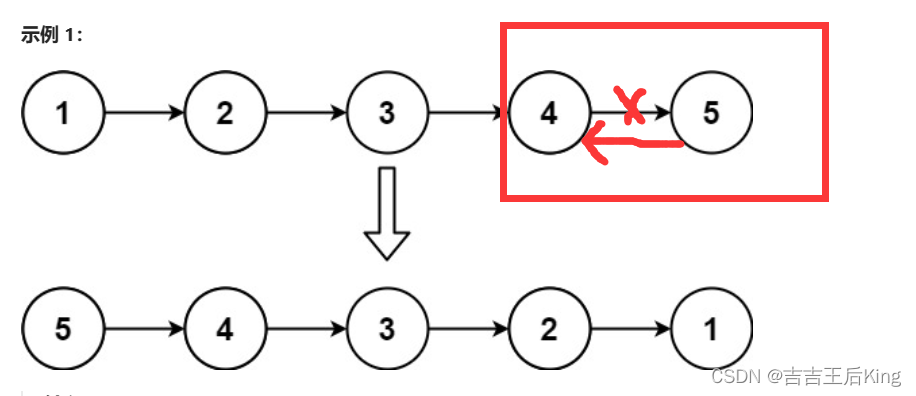
206.反转链表 这道题有两种解法,但不只有两种,嘿嘿。 法一:迭代法 就是按循序遍历将每一个指针的指向都给改了。比如说1——>2——>3改为null<——1<——2<——3这样。那这里以第二个结点为例,想一想。我想要指向…...

Python:核心知识点整理大全7-笔记
目录 4.2.5 遗漏了冒号 4.3 创建数值列表 4.3.1 使用函数 range() 4.3.2 使用 range()创建数字列表 结果如下: 4.3.3 对数字列表执行简单的统计计算 4.3.4 列表解析 4.4 使用列表的一部分 4.4.1 切片 4.4.2 遍历切片 4.4.3 复制列表 4.2.5 遗漏了冒号 fo…...
Hadoop学习笔记(HDP)-Part.15 安装HIVE
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
