图论-并查集
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题.一些常见的用途有求连通子图,求最小生成树Kruskal算法和最近公共祖先(LCA)等.
并查集的基本操作主要有:
.1.初始化
2.查询find
3.合并union
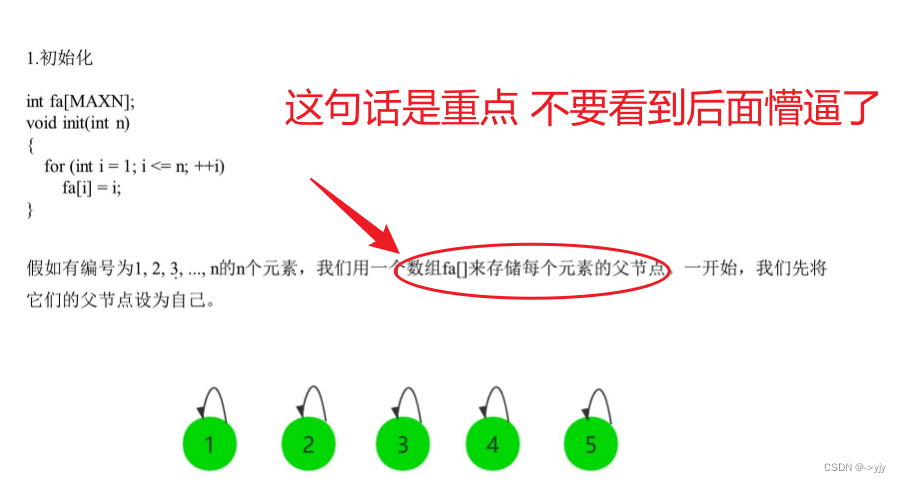

一般我们都会采用路径压缩 这样效率更加高



#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
#define MAXN 20001
int fa[MAXN];
void init(int n) {for (int i = 1; i <= n; i++) {fa[i] = i;}//初始化
}
int find(int x) {if (x == fa[x]) {return x;}else {fa[x] = find(fa[x]);//路径压缩 也就是一直找到祖先return fa[x];}
}
void unionn(int i, int j) {int i_fa = find(i);//找到i的祖先int j_fa = find(j);//找到j的祖先fa[i_fa] = j_fa;//i的祖先指向j的祖先 反过来也可以
}
int main() {int n, m, x, y, q;scanf("%d", &n);init(n);scanf("%d", &m);for (int i = 1; i <= m; i++) {scanf("%d%d", &x, &y);unionn(x, y);}scanf("%d", &q);for (int i = 1; i <= q; i++) {scanf("%d%d", &x, &y);if (find(x) == find(y)) {printf("Yes\n");}else {printf("No\n");}}return 0;
}
或者这样写
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 20010;int n, m;
int p[N];
int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) p[i] = i;while (m--) {int a, b;scanf("%d%d", &a, &b);p[find(a)] = find(b);//合并 a->b}scanf("%d,&m");while (m--) {int a, b;scanf("%d%d", &a, &b);if (find(a) == find(b))puts("yes");else puts("no");}return 0;}

#include<iostream>
using namespace std;const int N = 10010;int n, m;
int p[N];int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) p[i] = i;char op[2];//读入操作的字符串 因为字符串后面有'\0'所以要存多一位while (m--) {int a, b;scanf("%s%d%d",&op ,&a, &b);if(*op=='M')p[find(a)] = find(b);//合并else {if (find(a) == find(b)) {puts("Yes");}else {puts("No");}}}return 0;
}
#include<iostream>
using namespace std;
const int N = 10010;int n, m;
int p[N], s[N];int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}
int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) p[i] = i, s[i] = 1;while (m--){char op[3];int a, b;scanf("%s", &op);if (*op == 'C') {scanf("%d%d", &a, &b);a = find(a), b = find(b);if (a != b) {//如果相等证明他们在同一个祖先中s[b] += s[a];p[a] = b;}else if (*op == 'Q1') {scanf("%d%d", &a, &b);if (find(a) == find(b)) {puts("Yes\n");}else {puts("No\n");}}else {scanf("%d", &a);printf("%d\n", s[find(a)]);}}}return 0;
}
相关文章:

图论-并查集
并查集(Union-find Sets)是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题.一些常见的用途有求连通子图,求最小生成树Kruskal算法和最近公共祖先(LCA)等. 并查集的基本操作主要有: .1.初始化 2.查询find 3.合并union 一般我们都会采用路径压缩 这样…...
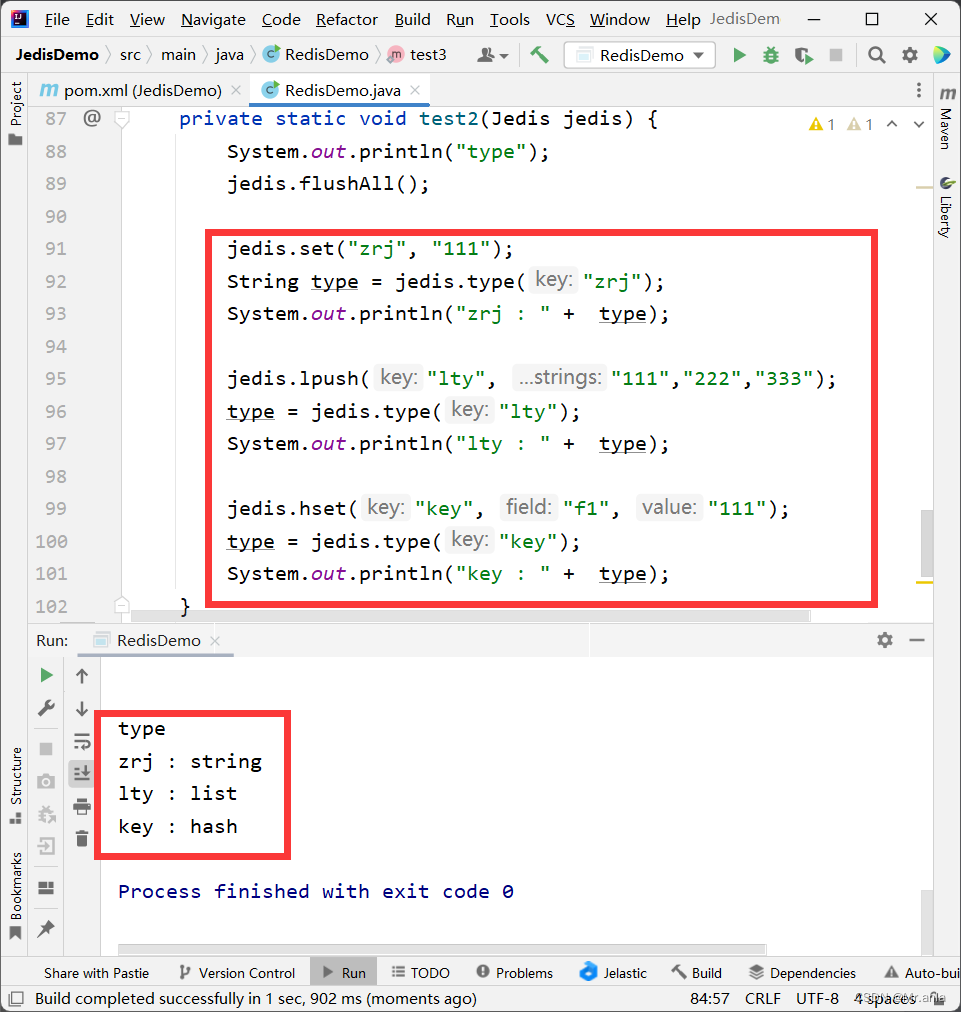
redis-学习笔记(Jedis 通用命令)
flushAll 清空全部的数据库数据 jedis.flushAll();set & get set 命令 get 命令 运行结果展示 exists 判断该 key 值是否存在 当 redis 中存在该键值对时, 返回 true 如果键值对不存在, 返回 false keys 获取所有的 key 值 参数是模式匹配 *代表匹配任意个字符 _代表匹配一…...
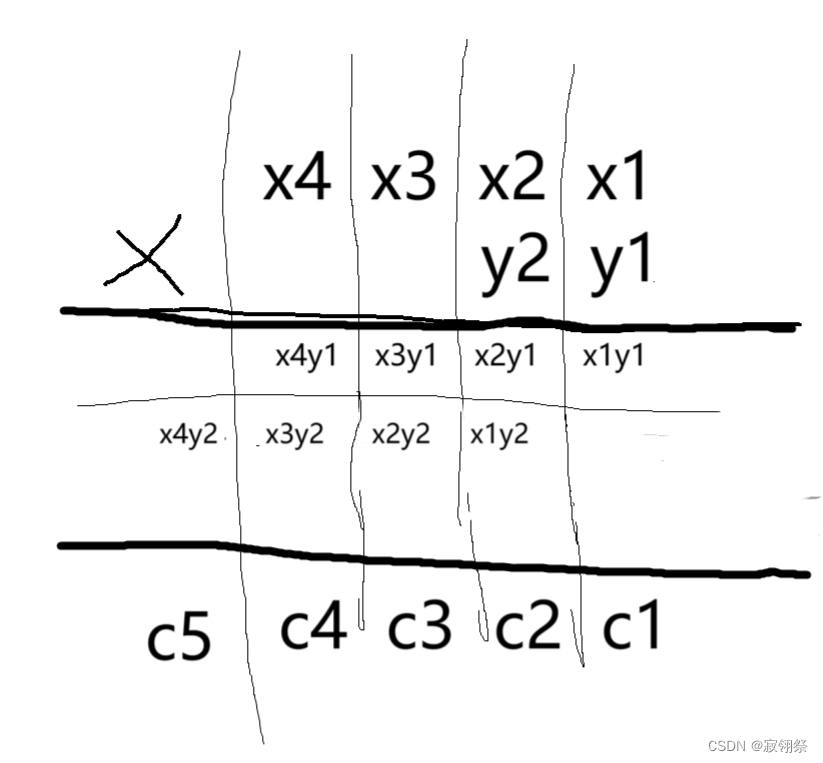
C语言:高精度乘法
P1303 A*B Problem - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 第一次画图,略显简陋。 由图可以看出c的小标与x,y下标的关系为x的下标加上y的下标再减一。 由此得到: c [ i j - 1 ] x [ i ] * y [ j ]x #include<stdio.h> #include<st…...

UE4 Niagara学习笔记
需要在其他发射器的同一个粒子位置发射其他粒子就用Spawn Particles from other Emitter 把发射器名字填上去即可 这里Move to Nearest Distance Field Subface GPU,可以将生成的Niagara附着到最近的物体上 使用场景就是做的火苗附着到物体上...

多维时序 | Matlab实现GA-LSTM-Attention遗传算法优化长短期记忆神经网络融合注意力机制多变量时间序列预测
多维时序 | MATLAB实现BWO-CNN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实现BWO-CNN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 多维时序 | Matlab实…...

LeetCode205. Isomorphic Strings
文章目录 一、题目二、题解 一、题目 Given two strings s and t, determine if they are isomorphic. Two strings s and t are isomorphic if the characters in s can be replaced to get t. All occurrences of a character must be replaced with another character wh…...

Event Driven设计模式
EDA(Event-Driven Architecture)是一种实现组件之间松耦合、易扩展的架构方式。一个最简单的EDA设计需要包含如下几个组件: Events:需要被处理的数据。一个Event至少包含两个属性,类型和数据,类型决定了Eve…...

PostgreSql 设置自增字段
一、概述 序列类型是 PostgreSQL 特有的创建一个自增列的方法。包含 smallserial、serial和 bigserial 类型,它们不是真正的类型,只是为了创建唯一标识符列而存在的方便符号。其本质也是调用的序列,序列详情可参考:《PostgreSql 序…...

什么是泊松图像混合
泊松图像混合(Poisson Image Editing)的原理基于泊松方程。该方法旨在保持图像中的梯度一致性,从而在图像编辑中实现平滑和无缝的混合。以下是泊松图像混合的基本原理和公式: 泊松方程 泊松方程是一个偏微分方程,通常…...

OpenAI 承认 ChatGPT 最近确实变懒,承诺修复问题
文章目录 一. ChatGPT 指令遵循能力下降引发用户投诉1.1 用户抱怨回应速度慢、敷衍回答、拒绝回答和中断会话 二. OpenAI 官方确认 ChatGPT 存在问题,展开调查三. OpenAI 解释模型行为差异,回应用户质疑四. GPT-4 模型变更受人事动荡和延期影响 一. Chat…...
———低代码:美味膳食或垃圾食品?)
创作活动(四十九)———低代码:美味膳食或垃圾食品?
#低代码:美味膳食或垃圾食品?# 一、什么是低代码 低代码是一种开发方法,通过可视化界面和少量的编码,使开发者能够快速构建应用程序。它的目标是提高开发效率、降低开发成本,并支持快速迭代和敏捷开发。 二、低代码的…...

【DL-TensorFlow遇错】TensorFlow中遇错合集
TensorFlow中遇错合集 一、AttributeError: module tensorflow has no attribute placeholder二、RuntimeError: tf.placeholder() is not compatible with eager execution. 一、AttributeError: module tensorflow has no attribute placeholder 错误原因 tensorflow版本问…...

pymysql代替mysqlclient,解决mysqlclient因版本不兼容无法安装成功而无法连接mysql的问题
pymysql代替mysqlclient,解决mysqlclient因版本不兼容无法安装成功而无法连接mysql的问题 原因:版本或者环境兼容问题,导致如centos或者其他Linux无法安装mysqlclient模块 解决办法:安装pymysql作为替代 在Django中连接MySQL数…...
uni-app 设置当前page界面进入直接变为横屏模式
首先 我们打开项目的 manifest.json 在左侧导航栏中找到 源码视图 然后找到 app-plus 配置 在下面加上 "orientation": [//竖屏正方向"portrait-primary",//竖屏反方向"portrait-secondary",//横屏正方向"landscape-primary",//横屏…...

Mysql的多表联合查询
内连接 隐式内连接 select column from tb1,tb2 where 条件; 显示内连接 关键字:[inner] join on 显示内连接与外连接的不同是新增的关键字,inner join 以及 使用on 替换了where select column from tb1 [inner] join tb2 on 条件; 外连接 左外…...

Linux上使用Python的requests库进行HTTP请求
在Linux上使用Python的requests库进行HTTP请求是一种非常方便和高效的方式。requests库是一个第三方库,用于发送HTTP请求并获取响应。下面是一个简单的示例,演示如何使用requests库发送GET请求并获取响应。 首先,你需要安装requests库。你可…...

图像处理领域的应用
图像处理领域的应用 文章目录 图像处理领域的应用1.图像类型2.图像转换3.彩色图像表示模式4.图像变换5.图像增强 1.图像类型 #mermaid-svg-x6mNS3Y1YkPvWUsQ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-x6mNS3Y1…...
MySQL笔记-第18章_MySQL8其它新特性
视频链接:【MySQL数据库入门到大牛,mysql安装到优化,百科全书级,全网天花板】 文章目录 第18章_MySQL8其它新特性1. MySQL8新特性概述1.1 MySQL8.0 新增特性1.2 MySQL8.0移除的旧特性 2. 新特性1:窗口函数2.1 使用窗口…...
C语言—每日选择题—Day46
第一题 1. 下列程序段的输出结果是() #include <stdio.h> int main() {int x 1,a 0,b 0;switch(x) {case 0: b;case 1: a;case 2: a;b;}printf("a%d,b%d\n", a, b);return 0; } A:a2,b1 B:a1,b1 C…...

flex布局,换行的元素上下设置间距
要生成的效果图如下: display:flexflex-direction: row;flex-wrap: wrap;当我们使用弹性盒子布局后,默认元素是没有外边距的,紧挨着样式就有点丑,如果想使换行后,元素的外边距有个距离,可以用如下方法解决…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
