AcWing 3709:单链表节点交换 ← 四川大学考研机试题
【题目来源】
https://www.acwing.com/problem/content/3712/
【题目描述】
输入一个单链表,依次交换前2个数,第3、4个数,第5、6个数,…,以此类推,直到操作完整个链表。
如果链表长度是奇数,则最后一个数不用操作。
输出交换之后的链表。
【输入格式】
第一行包含整数 n,表示节点数量。
第二行包含 n 个整数,表示每个节点的值。
【输出格式】
共一行,输出交换后的链表。
【数据范围】
1≤n≤100,
节点取值范围 [1,100]。
【输入样例】
5
1 2 3 4 5
【输出样例】
2 1 4 3 5
【算法分析】
本题是四川大学考研机试题。
在编码时,不要一看到单链表,就去用链式结构实现,这样就势必增加了编码复杂度。可以考虑用数组模拟实现,可大大简化编码难度。
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=105;
int a[maxn];int main() {int n;cin>>n;for(int i=1; i<=n; i++) cin>>a[i];int t=n;if(n%2!=0) t--;for(int i=1; i<t; i+=2) swap(a[i],a[i+1]);for(int i=1; i<=n; i++) cout<<a[i]<<" ";
}/*
in:
5
1 2 3 4 5out:
2 1 4 3 5
*/
相关文章:

AcWing 3709:单链表节点交换 ← 四川大学考研机试题
【题目来源】 https://www.acwing.com/problem/content/3712/【题目描述】 输入一个单链表,依次交换前2个数,第3、4个数,第5、6个数,…,以此类推,直到操作完整个链表。 如果链表长度是奇数,则最…...
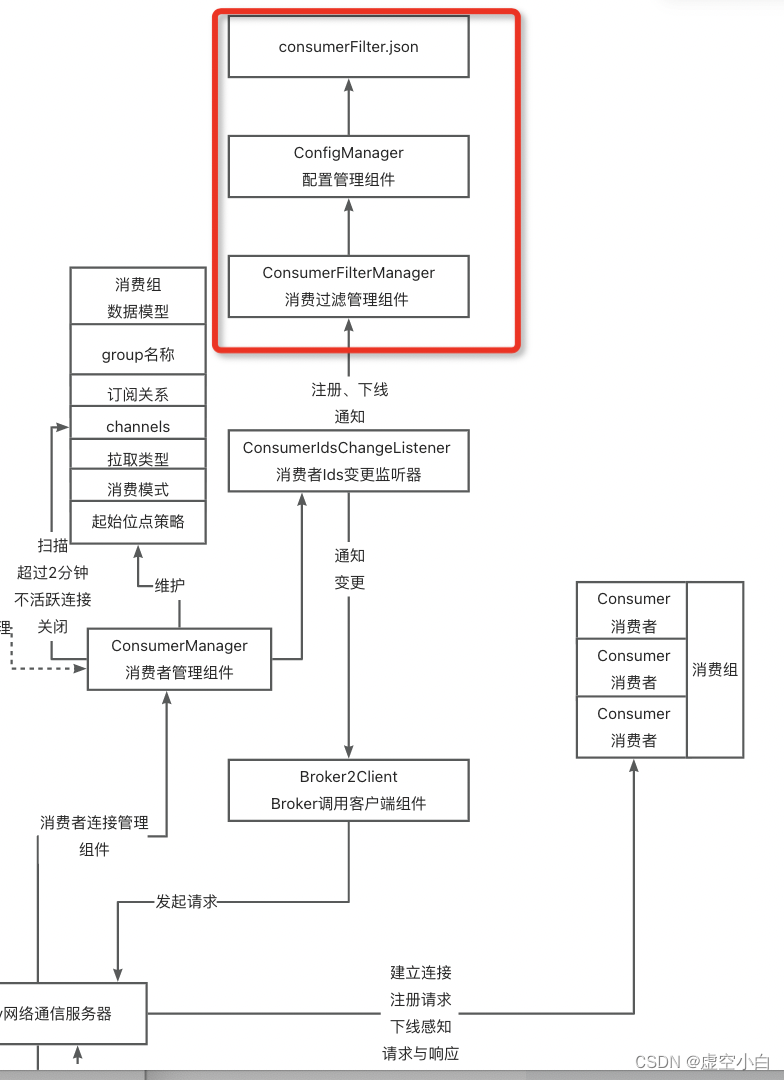
RocketMQ源码 Broker-ConsumerFilterManager 消费者数据过滤管理组件源码分析
前言 ConsumerFilterManager 继承了ConfigManager配置管理组件,拥有将内存数据持久化到磁盘文件consumerFilter.json的能力。它主要负责,对在消费者拉取消息时,进行消息数据过滤,且只针对使用表达式过滤的消费者有效。 源码版本&…...

数据挖掘-07-航空公司客户价值分析(包括数据和代码)
文章目录 0. 数据代码下载1. 背景与挖掘目标2. 导入相关库,加载数据2.1客户基本信息分布a. 绘制会员性别比例饼图b. 绘制会员各级别人数条形图c. 绘制年龄分布图 2.2 客户乘机信息分布分析a. 绘制客户飞行次数箱线图b. 绘制客户总飞行公里数箱线图 2.3 客户积分信息…...

浏览器 css 默认的字体图表
以下是一些常见的浏览器(PC端)中网站 CSS 默认字体及其对应的字体系列(font family): 浏览器默认字体字体系列(font family)ChromeArial, sans-serif“Arial”, “Helvetica Neue”, Helvetica…...

JAVA:注册表窗口的实现
目录 题目要求: 思路大意: 窗体的实现: 窗口A: 窗口B: 窗体之间的构思: 关键代码的实现: 窗口A: 封装列表: 窗口B: 题目要求: 使用…...

Liunx Centos 防火墙操作
liunx centos 防火墙 查看防火墙状态 systemctl status firewalld查看已经开放的端口 firewall-cmd --list-ports添加端口3306 firewall-cmd --zonepublic --add-port3306/tcp --permanent重启防火墙 firewall-cmd --reload数据库开放账号可以外网登陆 mysql -u root -p …...

VirtualBox 和 Vagrant 快速安装 Centos7 报错
VirtualBox 和 Vagrant 快速安装 Centos7 报错 今天尝试用 VirtualBox 和 Vagrant 快速安装 Centos7,BUG 多多! 1)下载 6.1.26 版本 VirtualBox,Windows11 不兼容???什么鬼? 解决…...

使用Python进行数学四则运算
当我们讨论到Python中的计算问题时,我们必然涉及到加法运算符()、减法运算符(-)、乘法运算符(*)以及除法运算符(/)这四大常见的算术运算。下面,我将为您展示如…...
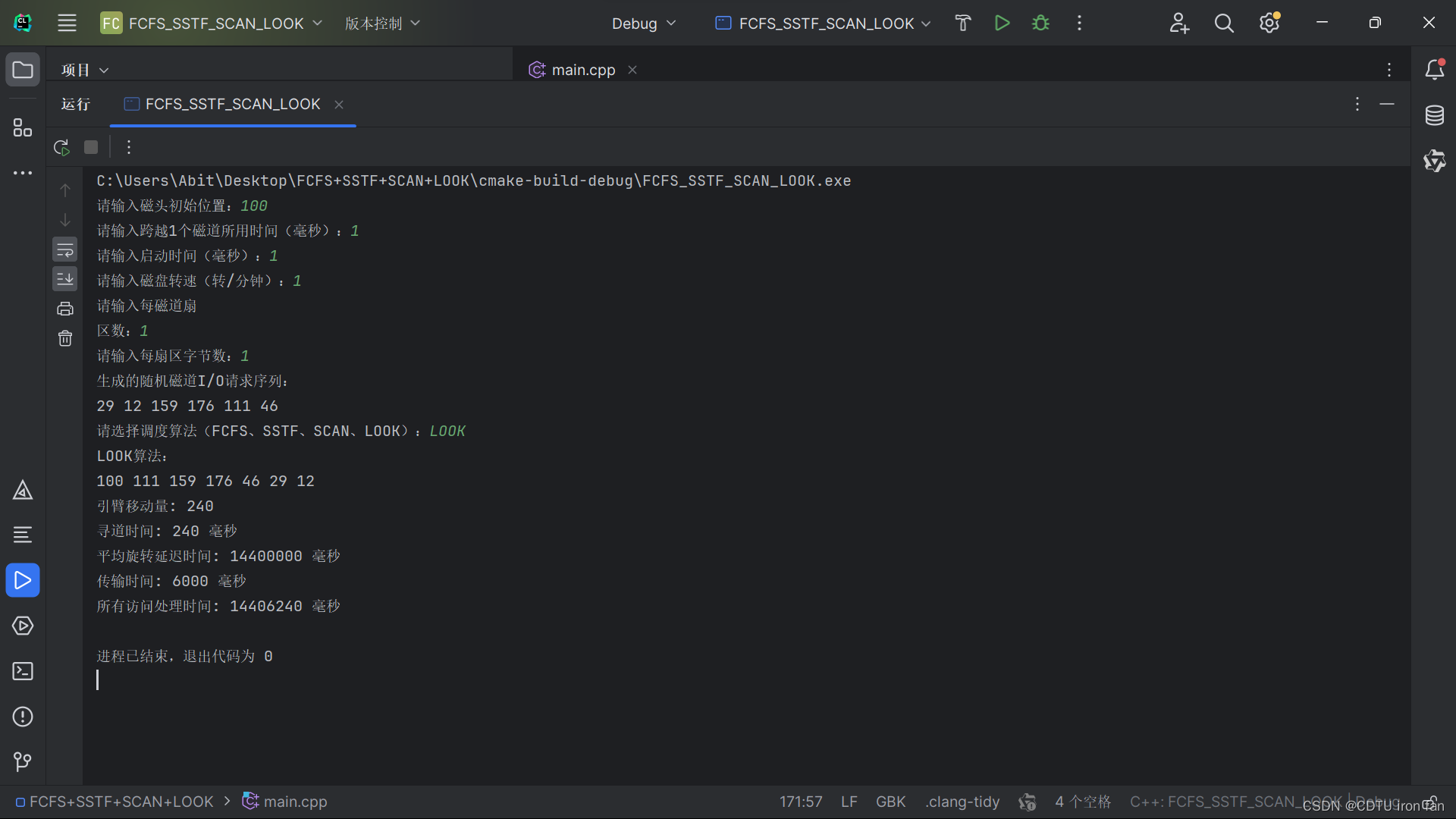
成都工业学院2021级操作系统专周课程设计FCFS,SSTF,SCAN,LOOK算法的实现
运行环境 操作系统:Windows 11 家庭版 运行软件:CLion 2023.2.2 源代码文件 #include <iostream> #include <vector> #include <algorithm> #include <random> using namespace std;// 生成随机数 int generateRandomNumber…...
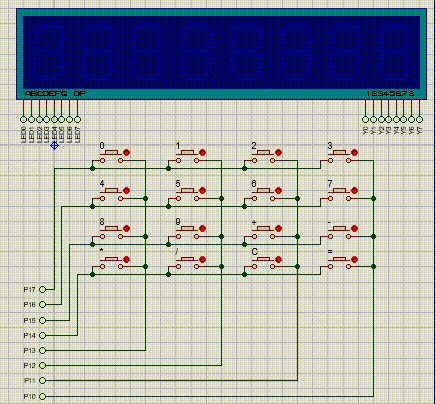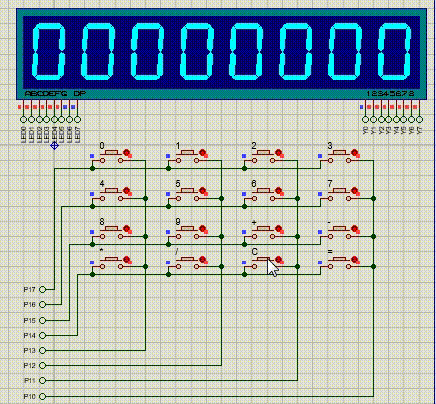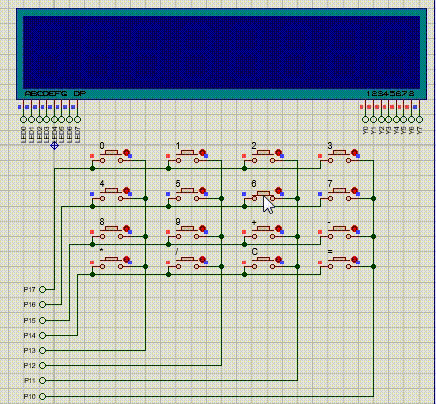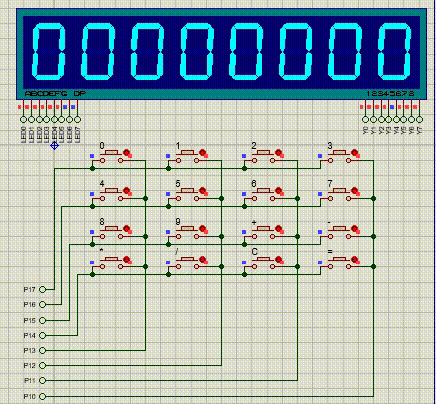
【51单片机系列】矩阵按键扩展实验
本文对矩阵按键的一个扩展,利用矩阵按键和动态数码管设计一个简易计算器。代码参考:https://blog.csdn.net/weixin_47060099/article/details/106664393 实现功能:使用矩阵按键,实现一个简易计算器,将计算数据及计算结…...

大数据云计算——Docker环境下部署Hadoop集群及运行集群案列
大数据云计算——Docker环境下部署Hadoop集群及运行集群案列 本文着重介绍了在Docker环境下部署Hadoop集群以及实际案例中的集群运行。首先,文章详细解释了Hadoop的基本概念和其在大数据处理中的重要性,以及为何选择在Docker环境下部署Hadoop集群。接着&…...
)
计算机网络链路层(期末、考研)
计算机网络总复习链接🔗 目录 组帧差错控制检错编码纠错编码 流量控制与可靠传输机制流量控制、可靠传输与滑动窗口机制单帧窗口与停止-等待协议多帧滑动窗口与后退N帧协议(GBN)多帧滑动窗口与选择重传协议 介质访问控制信道划分介质访问控制…...

洛谷 P8794 [蓝桥杯 2022 国 A] 环境治理
文章目录 [蓝桥杯 2022 国 A] 环境治理题目链接题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 思路解析CODE给点思考 [蓝桥杯 2022 国 A] 环境治理 题目链接 https://www.luogu.com.cn/problem/P8794 题目描述 LQ 国拥有 n n n 个城市,从 0 0 …...

力扣面试150题 | 买卖股票的最佳时期
力扣面试150题 | 买卖股票的最佳时期 题目描述解题思路代码实现 题目描述 121.买卖股票的最佳时期 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...
uniapp 之 图片 视频 文件上传
<view class"" style"padding: 24rpx 0"><text>相关资料 <text class"fs-26 color-666">(图片、视频、文档不超过9个)</text> </text><view class"flex align-center" style&…...

MIT线性代数笔记-第28讲-正定矩阵,最小值
目录 28.正定矩阵,最小值打赏 28.正定矩阵,最小值 由第 26 26 26讲的末尾可知在矩阵为实对称矩阵时,正定矩阵有以下四种判定方法(都是充要条件): 所有特征值都为正左上角所有 k k k阶子矩阵行列式都为正&…...
Python:五种算法RFO、GWO、DBO、HHO、SSA求解23个测试函数
一、五种算法介绍 (1)红狐优化算法(Red fox optimization,RFO) (2)灰狼优化算法(Grey Wolf Optimizer,GWO) (3)蜣螂优化算法(Dung beetle opti…...

如何参与开源项目
大家好,受卡哥邀请,和大家分享一下开源活动的相关经验。首先简要自我介绍一下,我目前在一所985研二在读,主要学习大数据方向,从去年开始参与开源活动近一年时间,也对多个Apache框架有所贡献。 由于学校或专…...
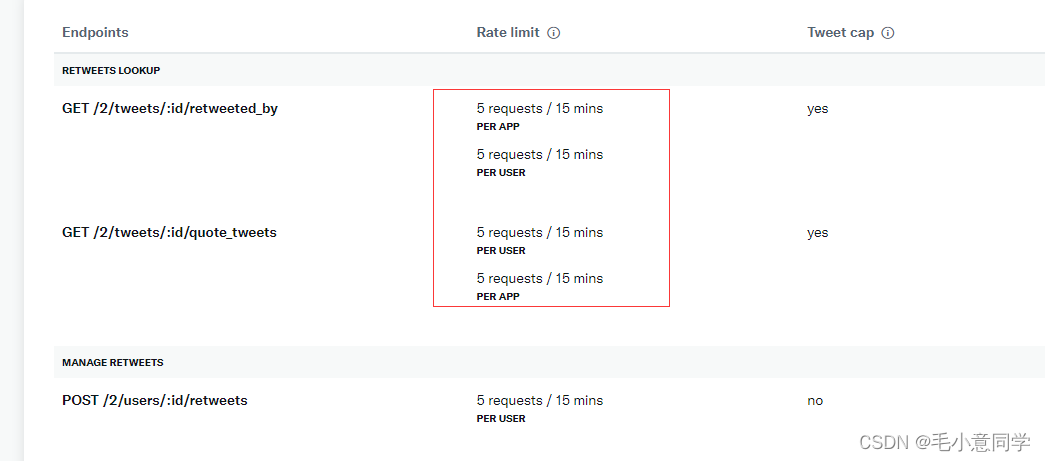
twitter开发如何避坑
此篇介绍在twitter开发过程中遇到的坑(尤其是费用的坑)。 一坑:免费接口少! 刚开始申请免费API使用的时候,twitter官方只会给你三个免费接口使用。 发twitter、删推文、查看用户信息。 这三个接口远远不够开发中使用…...
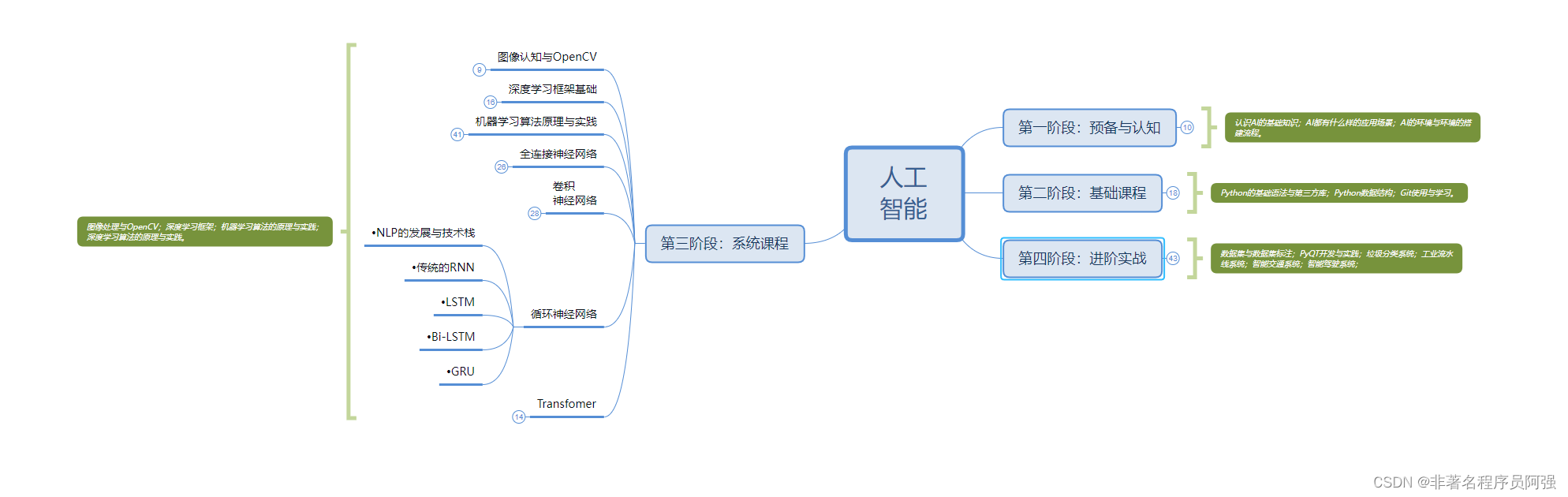
人工智能算法合集
人工智能(Artificial Intelligence,AI)作为当今世界最热门的技术领域之一,正日益改变着我们的生活方式、工作方式甚至整个社会结构。在人工智能领域中,算法是至关重要的一环,它们是实现人工智能技术应用的核…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
