Logistic Regression——逻辑回归
1. 为什么需要逻辑回归
在前面学习的线性回归中,我们的预测值都是任意的连续值,例如预测房价。除此之外,还有一个常见的问题就是分类问题,而逻辑回归是一个解决分类问题的模型,其预测值是离散的。
分类问题又包括二分类问题与多分类问题,对于二分类问题来说,预测值只可能是\否即1\0,

对于多分类问题来说,预测值可能是多个分类中的一个,例如我输入的是一些动物的图片,我想让模型辨认这些是什么动物,我可以设定预测值1代表模型认为输入是一只猫,预测值2代表模型认为输入是一只狗,预测值3代表模型认为输入是一只猪。
2. 二分类逻辑回归
2.1 从线性回归到分类
如果有这样一个场景,输入x为肿瘤的大小,而需要预测是否是恶性的。接下来我们仍然使用线性回归模型,但如果我们这增设这样一个阈值

这样一来,所有预测值都将变成1或者0,实现了分类的目的

2.2 逻辑回归模型
对于线性回归的模型来说,其输出值是任意的,常常会远远大于1或者远远小于0,仅仅上述的阈值可能并不会起到作用或者效果很差。
对此,逻辑回归会先将所有预测值通过sigmoid 函数映射到[0,1]区间,函数表达式和图像如下图
 (z为输入)
(z为输入)

sigmoid 函数是一个非线性函数,当x大于0时,输出值大于0.5,当x<0时输出值小于0.5
最终我们得到逻辑回归的模型如下

作用是,对于给定的输入变量,通过参数
计算输出变量为1的可能性是多少
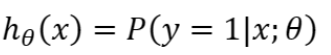
假如对于一个输入x,最终计算出=0.7,则模型认为有70%的可能其为正向类(=1),相反负向类的可能性就为1-0.7=0.3
最后在分类时,再入加上之前的阈值

所以逻辑回归就是线性回归再嵌套一个非线性的sigmoid函数,其本质还是回归
2.4 决策边界(Decision Boundary)
假如分类这样一些数据,‘x’为1,圈为0

通过建立逻辑回归模型

假设经过训练我们得到了这样一组参数![]() ,于是得到嵌套在逻辑回归里的线性回归模型
,于是得到嵌套在逻辑回归里的线性回归模型,根据逻辑回归的原理当
时预测1,当
时预测0,于是分隔情况就是
,我们可以画出这个直线
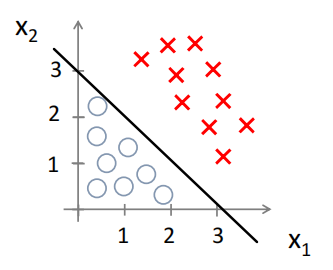
这条线便是模型的决策边界
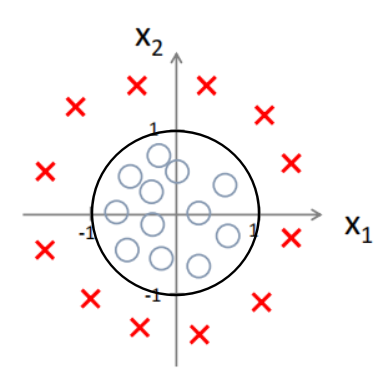
如果是这样的数据

建立逻辑回归模型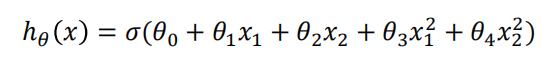 、
、
得到参数
![]()
同样的原理,得到其决策边界,是一个圆心在原点,半径为1的圆
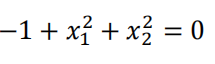
2.5 损失函数
2.5.1 为什么不用MSE损失函数
根据上述的理论可以知道,逻辑回归的和线性回归的本质是一样的。那是不是意味着损失函数也可以用MSE。
在线性回归中损失函数如下
我们将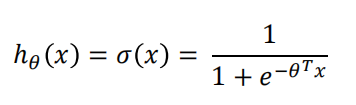 带入可以得到
带入可以得到
得到的是一个非凸函数(non-convexfunction),这会很大程度上影响梯度下降法寻找全局最小值,很可能停留在在某个局部极小值
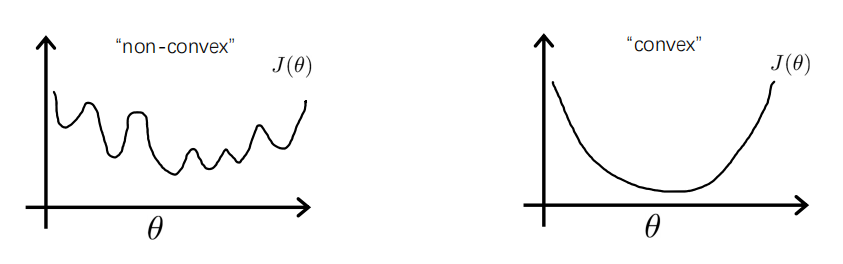
2.5.2 对数损失函数
介于上述问题,对于二分类逻辑回归来说,使用的是对数损失函数。
对于一个样本来说,预测值会有1和0两种情况,对应两个损失值

(log一般以e为底)
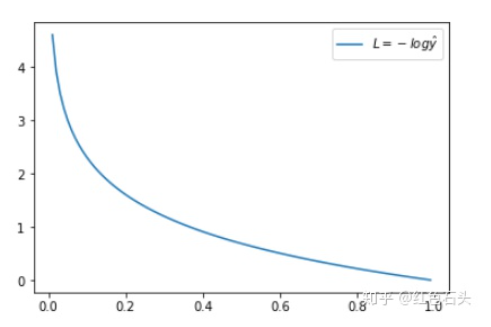
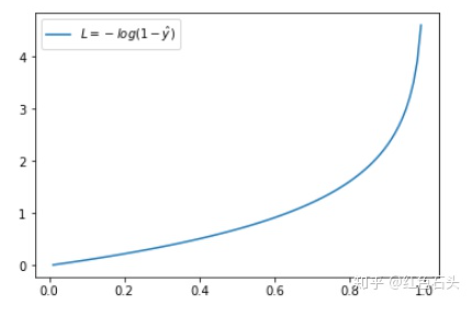
当实际y=1时,如果预测值=1,此时预测是完全正确的,代入上式计算误差为0,如果预测值
不为1,代表模型没有100%的把握认为这是正向类的,此时误差会随着
的减小而变大。
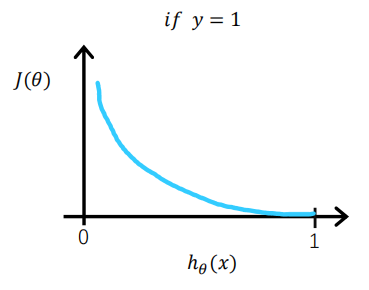
当实际y=0时,如果预测值=0,此时预测是完全正确的,代入上式计算误差为0,如果预测值
不为0,代表模型没有100%的把握认为这是负向类的,此时误差会随着
的增大而变大。
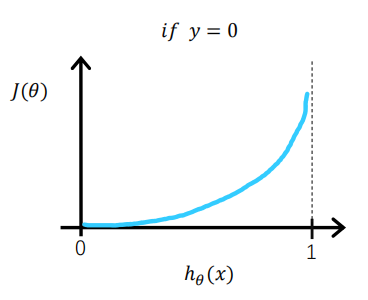
将这两种情况合在一起
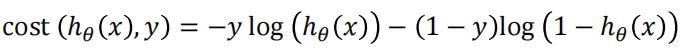
再求和取平均得到最终损失函数表达式
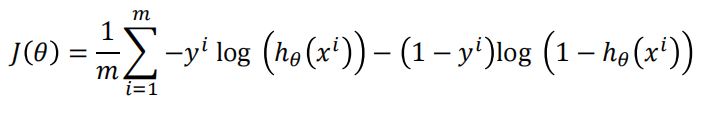
采用矩阵的形式表达
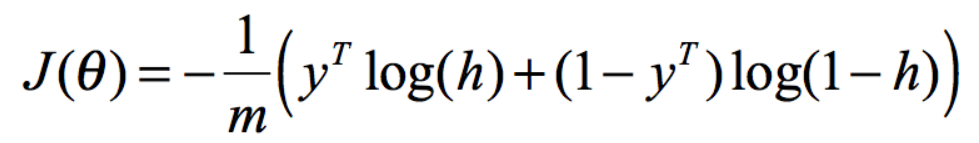
2.6 梯度下降
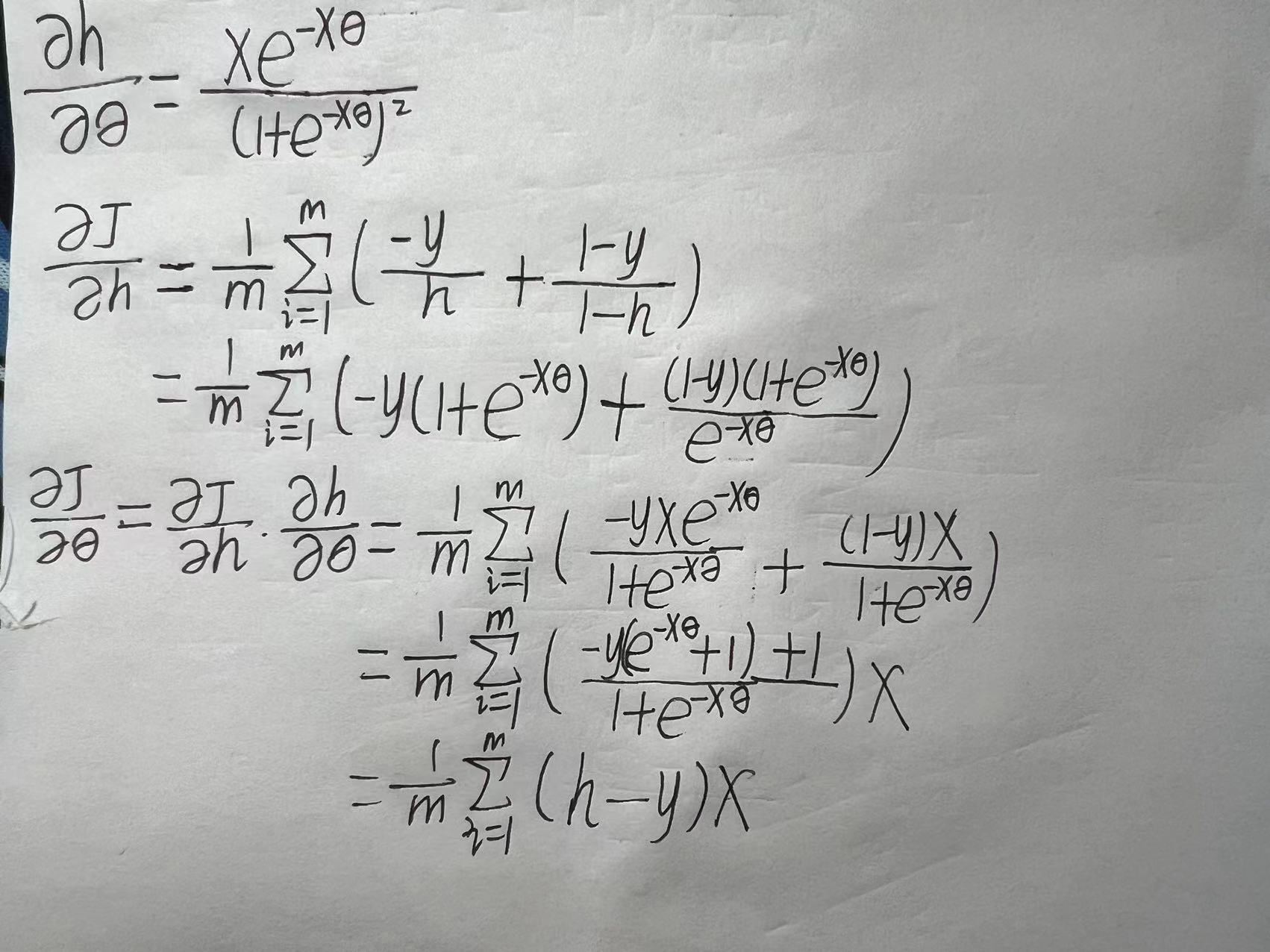
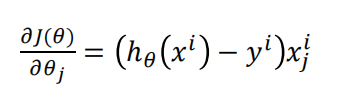
矩阵表达式为

使用梯度下降

矩阵表达式为
3. 多分类逻辑回归
多分类逻辑回归的实现依赖于二分类
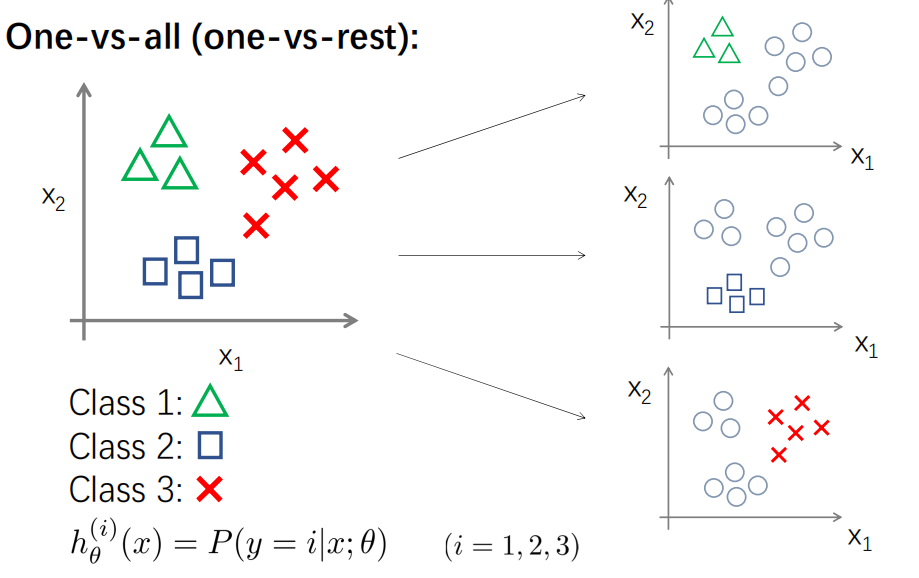
将其中一个类标记为正向类,然后将其他类都标记为负向类,得到一个模型,接着选择另外一个类标记为正向类,然后将其他类都标记为负向类,又得到一个模型
,以此类推,我们可以得到一系列模型,假设有k个类
,i=(1,2,3,4……k)
训练好这一系列模型后,对于一个输入x,让其在所有的分类器都得到一个输出,最后选择一个max作为最终的输出
4. 逻辑回归的实例
ex2data1数据集包含100行数据前两列是学生的两种考试的成绩,最后一列是他们被是否录取。需要根据学生的两种考试的成绩来预测他们被是否录取。
1.读取数据集
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltdata = pd.read_csv('ex2data1.txt',names=['exam1','exam2','admitted'])
data.head()
# 根据admitted的值分类
plt.scatter(positive['exam1'],positive['exam2'],marker='o',label='Admitted')
plt.scatter(negative['exam1'],negative['exam2'],marker='x',label='Not Admitted')
plt.xlabel('Exam1 Score')
plt.ylabel('Exam2 Score')
plt.legend()
plt.show()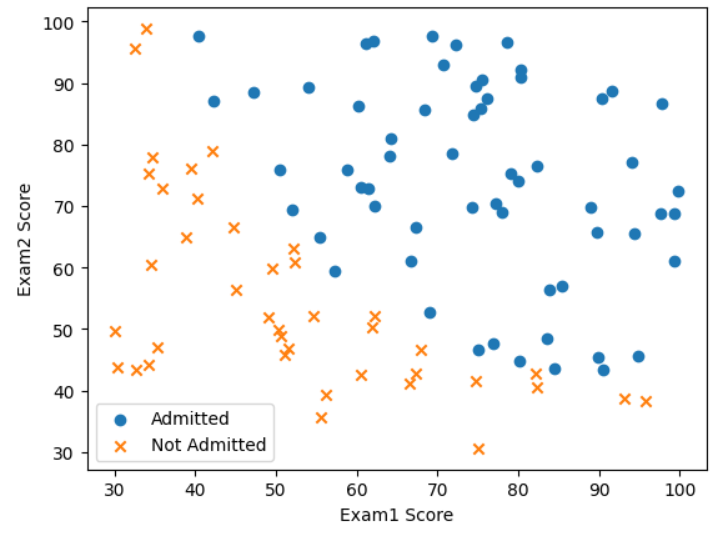
2.数据预处理
data.insert(0,'ones',1)
X = data.iloc[:,0:-1].values
y = data.iloc[:,-1].values
y = y.reshape(100,1)3.定义Sigmoid函数
def sigmoid(z):return 1/(1+np.exp(-z))4.定义损失函数
def lossFunction(X,y,theta):m = len(X)h = sigmoid(X@theta)return (1/m)*np.sum(-y.T@np.log(h)-(1-y).T@np.log(1-h))5.模型训练
def train(X,y,alpha,epochs):loss_history = []theta = np.random.rand(3,1)for i in range(epochs):m = len(X)h = sigmoid(X@theta)theta = theta - (alpha/m)*X.T@(h-y)current_loss = lossFunction(X,y,theta)loss_history.append(current_loss) if (i+1) % 100 == 0:print("epochs={},current_loss={}".format(i+1,current_loss))# 绘制损失函数图像plt.plot(range(1,epochs+1),loss_history)plt.xlabel('epochs')plt.ylabel('loss')plt.title('Loss Curve')plt.show()return theta# 参数
alpha = 0.1
epochs = 1000
theta = train(X,y,alpha,epochs)
admitted = X[y.flatten() == 1]
not_admitted = X[y.flatten() == 0]
plt.scatter(admitted[:, 1], admitted[:, 2], label='Admitted', marker='o')
plt.scatter(not_admitted[:, 1], not_admitted[:, 2], label='Not Admitted', marker='x')
plt.xlabel('Exam 1 score')
plt.ylabel('Exam 2 score')# 绘制决策边界
plot_x = np.array([min(X[:, 1]) - 2, max(X[:, 1]) + 2])
plot_y = (-1 / theta[2]) * (theta[1] * plot_x + theta[0])
plt.plot(plot_x, plot_y, label='Decision Boundary')
plt.legend()
plt.show() 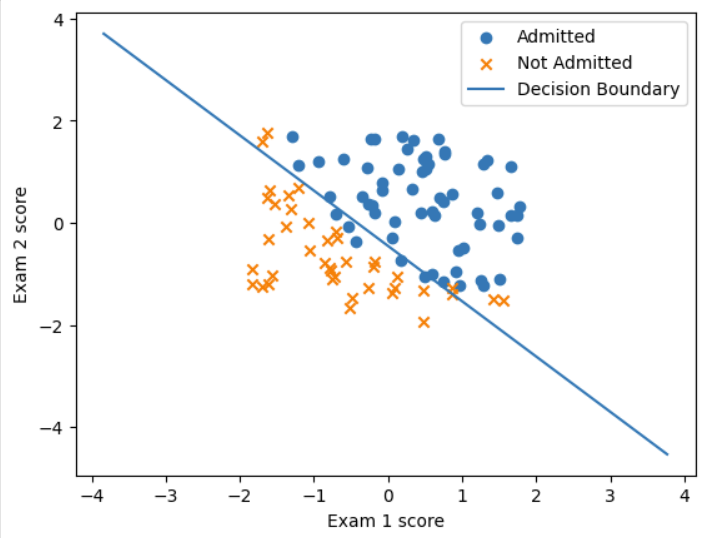
相关文章:

Logistic Regression——逻辑回归
1. 为什么需要逻辑回归 在前面学习的线性回归中,我们的预测值都是任意的连续值,例如预测房价。除此之外,还有一个常见的问题就是分类问题,而逻辑回归是一个解决分类问题的模型,其预测值是离散的。 分类问题又包括…...
跟随鼠标动态显示线上点的值(基于Qt的开源绘图控件QCustomPlot进行二次开发)
本文为转载 原文链接: 采用Qt快速绘制多条曲线(折线),跟随鼠标动态显示线上点的值(基于Qt的开源绘图控件QCustomPlot进行二次开发) 内容如下 QCustomPlot是一个开源的基于Qt的第三方绘图库,能…...
Todesk、向日葵等访问“无显示器”主机黑屏问题解决
我的环境是 ubuntu 22.04 安装 要安装 video dummy,请在终端中运行以下命令: sudo apt install xserver-xorg-video-dummy配置 video dummy 的配置文件请自行搜索 使用任何文本编辑器打开此文件。 我的是 /etc/X11/xorg.conf 默认配置文件包含以下内…...

maven打包插件maven-jar-plugin与spring-boot-maven-plugin
maven几种打包插件介绍 文章目录 🔊1.spring-boot-maven-plugin打包后效果 📕2.maven-jar-plugin打包后效果🖊️最后总结 🔊1.spring-boot-maven-plugin <plugins><plugin><groupId>org.springframework.boot&…...

uniapp微信小程序下载base64图片流或https图片
常规https的图片下载是这样的 const urlPath https://test/logo.png uni.downloadFile({url: urlPath,success(res){// 这时会产生一个临时路径,在应用本次启动期间可以正常使用。if (res.statusCode 200) {// 需要将图片保存到相册uni.saveImageToPhotosAlbum({…...
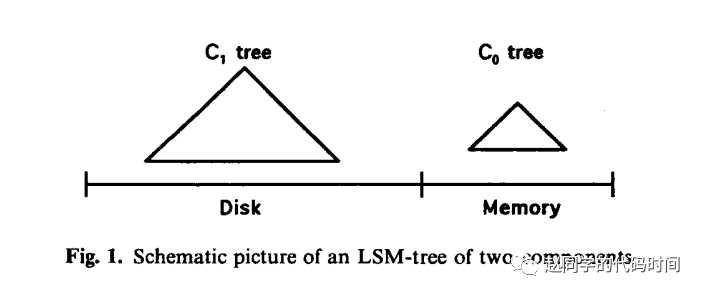
数据结构 | Log-Structured Merge Tree (LSM Tree)
今天介绍LSM Tree这个数据结构,严格意义上来说,他并不像他的名字一样是一棵树型的数据结构,而更多是一种设计思想。 LSM Tree最先在1996年被提出,后来被广泛运用于现代NoSQL(非关系型数据库)系统中…...
)
QEMU源码全解析 —— virtio(9)
接前一篇文章: 上两回讲解了virtio balloon相关类所涉及的realize函数以及大致流程,如下表所示: realize函数parent_dc_realize函数DeviceClassvirtio_pci_dc_realizePCIDeviceClassvirtio_pci_realizeVirtioPCIClassvirtio_balloon_pci_rea…...
金蝶云星空协同开发环境应用内执行单据类型脚本
文章目录 金蝶云星空协同开发环境应用内执行单据类型脚本业务界面查询单据类型表数据导出数据执行数据库脚本单据类型xml检验是否执行成功检查数据库检查业务数据 金蝶云星空协同开发环境应用内执行单据类型脚本 业务界面 查询单据类型表数据 先使用类型中文在单据类型多语言…...

矩阵理论及其应用邱启荣习题3.5题解
(1) P ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} −1−110−1112−1 A ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmat…...
-------连载(49))
Java面试题(每天10题)-------连载(49)
目录 Tomcat篇 1、Tomcat的缺省端口是多少?怎么修改? 2、Tomcat有哪几种Connector运行模式(优化)? 3、Tomcat有几种部署方式? 4、Tomcat容器时如何创建servlet类实例?用到了什么原理&…...

python——数据类型
数据类型目录 前言一、Number(数字)数字类型转换:二、String(字符串)常用字符串运算符:字符串格式化:三、Tuple(元组)常用运算符四、List(列表)嵌套列表:常用列表操作:五、Dictionary(字典)六、Set(集合)...

hive中如何求取中位数?
目录 中位数的概念代码实现准备数据实现 中位数的概念 中位数(Median)又称中值,统计学中的专有名词,是按顺序排列的一组数据中居于中间位置的数,代表一个样本、种群或概率分布中的一个数值,其可将数值集合…...

在C#中异步编程
在C#中,异步编程是一种编写并发和响应式代码的技术,通过将耗时的操作放在后台线程中执行,以避免阻塞主线程,提高程序的性能和响应性。异步编程使用async和await关键字,结合任务(Task)和异步操作…...

微服务保护--Feign整合Sentinel
限流是一种预防措施,虽然限流可以尽量避免因高并发而引起的服务故障,但服务还会因为其它原因而故障。而要将这些故障控制在一定范围,避免雪崩,就要靠线程隔离(舱壁模式)和熔断降级手段了。 线程隔离之前讲到…...

二进制to十六进制
输入小于等于十六位的二进制数据,输出十六进制数据; #include <stdio.h> #include <stdlib.h> #include <math.h>int main(void) {char arr[16] { 0 }; int array[16] { 0 }; int hex[4] { 0 };int i 0; int num 0;scanf("…...

Logistic 回归算法
Logistic 回归 Logistic 回归算法Logistic 回归简述Sigmoid 函数Logistic 回归模型表达式求解参数 $\theta $梯度上升优化算法 Logistic 回归简单实现使用 sklearn 构建 Logistic 回归分类器Logistic 回归算法的优缺点 Logistic 回归算法 Logistic 回归简述 Logistic 回归是一…...
ubuntu安装详细步骤
一,先下载vmware 1,第一步打开上面链接 下载网址 : https://www.vmware.com/products/workstation-pro/wo rkstation-pro-evaluation.html 许可证 JU090-6039P-08409-8J0QH-2YR7F ZF3R0-FHED2-M80TY-8QYGC-NPKYF FC7D0-D1YDL-M8DXZ-CYPZE-P2AY6 ZC3T…...

力扣5. 最长回文子串
动态规划 思路: 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果;那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j]);长度为1的字符串都是回文; 原字符串长度为1,是回文;原字符串子串长度为1ÿ…...

肆[4],函数VectorToHomMat2d/AffineTransPoint2d
函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...

下载文件 后端返回给前端 response header 响应头
当浏览器在请求资源时,会通过http返回头中的content-type决定如何显示/处理将要加载的数据,如果这个类型浏览器能够支持阅览,浏览器就会直接展示该资源,比如png、jpeg、video等格式。在某些下载文件的场景中,服务端可能…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
