RecyclerView中的设计模式解读
一.观察者模式:(待完善,这个写的不咋地,没理解透彻)
1.观察者模式的概念:
(1)消息传递方向:被观察者->观察者
(2)代码实现:
首先具有一个接口,该接口是所有观察者的父接口,各个子观察者通过实现这个接口来实例化一个观察者对象,而被观察者会持有观察者对象的引用。至于怎么将观察者对象传给这个引用的方法有很多,比如通过在被观察者对象类里面写set方法让观察者对象来调用、利用构造函数的参数传递等等。
(3)快速记忆:
被观察者:持有引用;在什么时候去做这件事情;
观察者:实现接口;具体做什么事情;
2.RecyclerView中的观察者模式:
(1)简介:RecyclerView中的Adapter的整体实现就是一个观察者模式
(2)源码分析:(以notifyDataSetChanged()为例)
<1>RecyclerView中的Adapter,是一个内部静态类:
public abstract static class Adapter<VH extends RecyclerView.ViewHolder> {//被观察者private final RecyclerView.AdapterDataObservable mObservable = new RecyclerView.AdapterDataObservable();//注册观察者public void registerAdapterDataObserver(@NonNull RecyclerView.AdapterDataObserver observer) {this.mObservable.registerObserver(observer);}//注销观察者public void unregisterAdapterDataObserver(@NonNull RecyclerView.AdapterDataObserver observer) {this.mObservable.unregisterObserver(observer);}//调用被观察者的方法public final void notifyDataSetChanged() {this.mObservable.notifyChanged();}}
<2>AdapterDataObservable ,被观察者对象类:
static class AdapterDataObservable extends Observable<RecyclerView.AdapterDataObserver> {public void notifyChanged() {for(int i = this.mObservers.size() - 1; i >= 0; --i) {//遍历所有的子观察者,调用子观察者的onChanged()方法((RecyclerView.AdapterDataObserver)this.mObservers.get(i)).onChanged();}}}<3>AdapterDataObserver 类,调用onChanged()方法,这是抽象类:
public abstract static class AdapterDataObserver {public void onChanged() {}}<4>RecyclerViewDataObserver 类,为AdapterDataObserver类的实现类,真正调用onChanged()方法的地方:
private class RecyclerViewDataObserver extends RecyclerView.AdapterDataObserver {public void onChanged() {RecyclerView.this.assertNotInLayoutOrScroll((String)null);RecyclerView.this.mState.mStructureChanged = true;RecyclerView.this.processDataSetCompletelyChanged(true);if (!RecyclerView.this.mAdapterHelper.hasPendingUpdates()) {//重新绘制界面RecyclerView.this.requestLayout();}}}
<5>setAdapter()方法,调用此方法来设置adapter:
public void setAdapter(@Nullable RecyclerView.Adapter adapter) {this.setLayoutFrozen(false);this.setAdapterInternal(adapter, false, true);this.processDataSetCompletelyChanged(false);this.requestLayout();}<6>setAdapterInternal()方法
private void setAdapterInternal(@Nullable RecyclerView.Adapter adapter, boolean compatibleWithPrevious, boolean removeAndRecycleViews) {if (this.mAdapter != null) {//注销观察者this.mAdapter.unregisterAdapterDataObserver(this.mObserver);this.mAdapter.onDetachedFromRecyclerView(this);}if (adapter != null) {//注册观察者adapter.registerAdapterDataObserver(this.mObserver);adapter.onAttachedToRecyclerView(this);}}(3)总结:
Recyclerview中的Adapter可以理解为观察者的父类,我们可以自己实现一个继承自Recyclerview中的Adapter的子类,也就是实例化一个观察者对象。然后通过Recyclerview中的setAdapter()方法可以将这个对象设置给被观察者。例如此时在这个对象中调用notifyDataSetChanged()方法,那么最终会调用被观察者的notifyChanged()方法。
二.其他(待更新)
RecyclerView 中的设计模式 | Agehua
相关文章:

RecyclerView中的设计模式解读
一.观察者模式:(待完善,这个写的不咋地,没理解透彻) 1.观察者模式的概念: (1)消息传递方向:被观察者->观察者 (2)代码实现: 首…...

ACwing算法备战蓝桥杯——Day30——树状数组
定义: 树状数组是一种数据结构,能将对一个区间内数据进行修改和求前缀和的这两种操作的最坏时间复杂度降低到O(logn); 实现所需变量 变量名变量数据类型作用数组a[]int存储一段区间数组tr[]int表示树状数组 主要操作 函数名函数参数组要作用lowbit()int…...
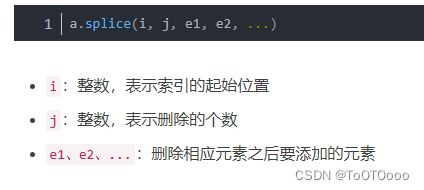
elementui + vue2实现表格行的上下移动
场景: 如上,要实现表格行的上下移动 实现: <el-dialogappend-to-bodytitle"条件编辑":visible.sync"dialogVisible"width"60%"><el-table :data"data1" border style"width: 100%&q…...
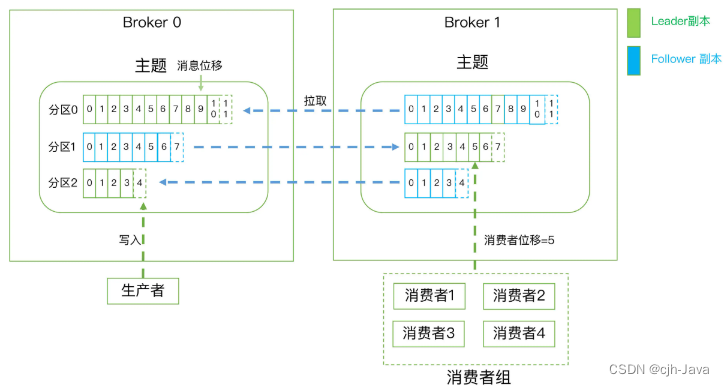
2、快速搞定Kafka术语
快速搞定Kafka术语 Kafka 服务端3层消息架构 Kafka 客户端Broker 如何持久化数据小结 Kafka 服务端 3层消息架构 第 1 层是主题层,每个主题可以配置 M 个分区,而每个分区又可以配置 N 个副本。第 2 层是分区层,每个分区的 N 个副本中只能有…...

CSS新手入门笔记整理:CSS3选择器
属性选择器 属性选择器,指的是通过“元素的属性”来选择元素的一种方式。 语法 元素[attr^"xxx"]{} 元素[attr$"xxx"]{} 元素[attr*"xxx"]{} 选择器 说明 E[attr^"xxx"] 选择元素E,其中E元素的attr属性是…...
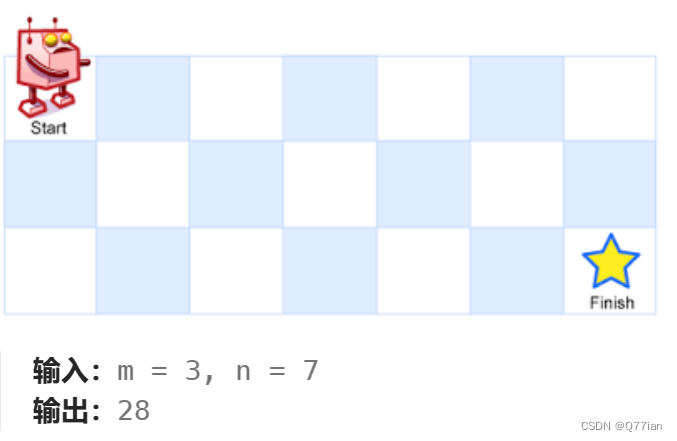
D34|不同路径
62.不同路径 初始思路: 1)确定dp数组以及下标的含义: dp[i][i]存放到第i1行和第i1列的方法数 2)确定递推公式: dp[i][i] dp[i -1][i] dp[i][i-1] 3)dp数组如何初始化 第0行是1; 第0列是1&a…...
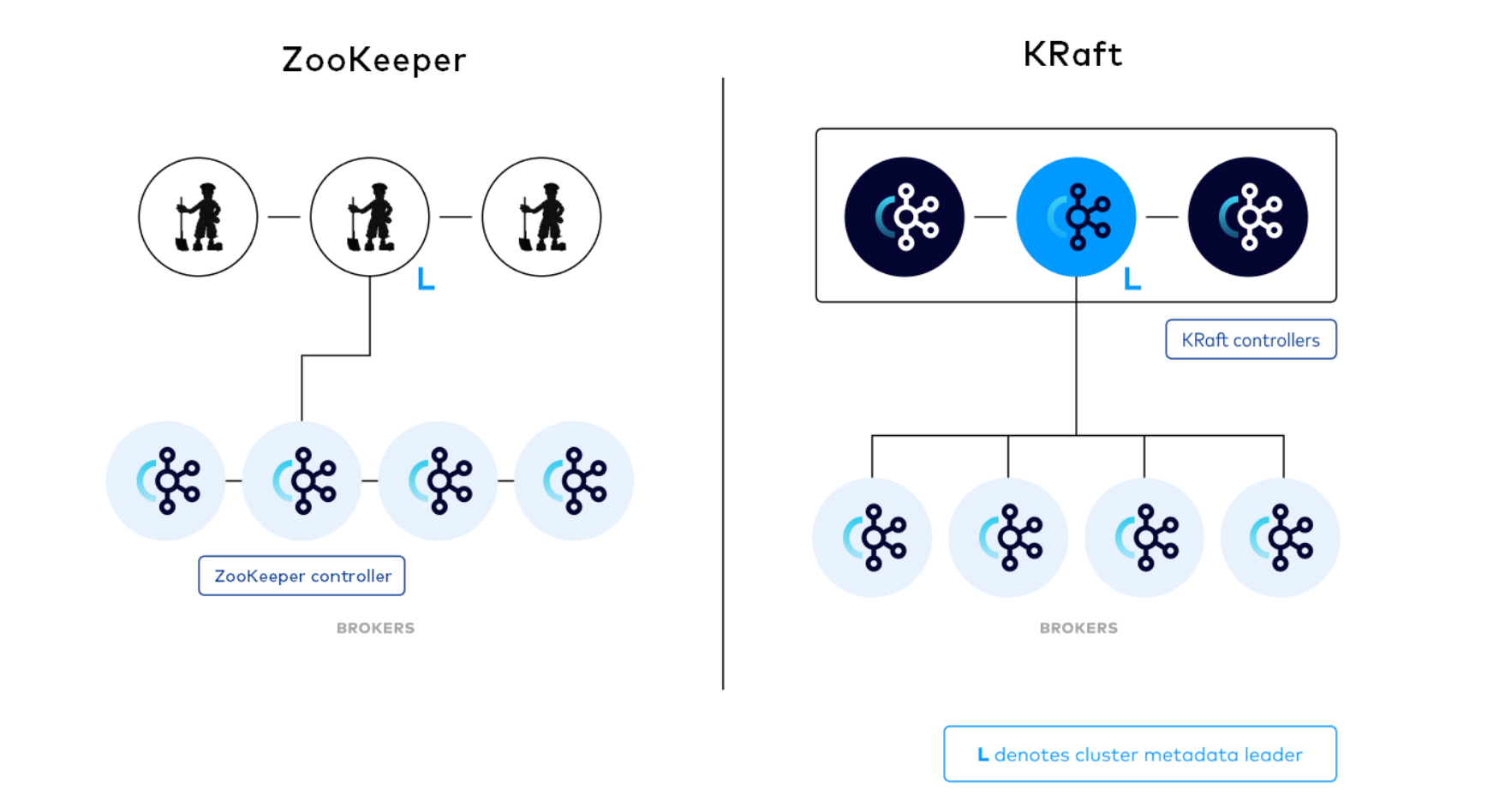
【运维】Kafka高可用: KRaft(不依赖zookeeper)集群搭建
文章目录 一. kafka kraft 集群介绍1. KRaft架构2. Controller 服务器3. Process Roles4. Quorum Voters5. kraft的工作原理 ing 二. 集群安装1. 安装1.1. 配置1.2. 格式化 2. 启动测试2.1. 启功节点服务2.2. 测试 本文主要介绍了 kafka raft集群架构: 与旧架构的不…...

Python 自动化之批量处理文件(一)
批量新建目录、文档Pro版本 文章目录 批量新建目录、文档Pro版本前言一、做成什么样子二、基本思路1.引入库2.基本架构 三、用户输入模块四、数据处理模块1.excel表格数据获取2.批量数据的生成 总结 前言 我来写一个不一样的批量新建吧。在工作中,有些同学应该会遇…...

力扣72. 编辑距离
动态规划 思路: 假设 dp[i][j] 是 word1 前 i 个字母到 word2 前 j 个字母的编辑距离;那么状态 dp[i][j] 状态的上一个状态有: dp[i - 1][j],word1 前 i - 1 个字母到 word2 前 j 个字母的编辑距离,此状态再插入一个字…...
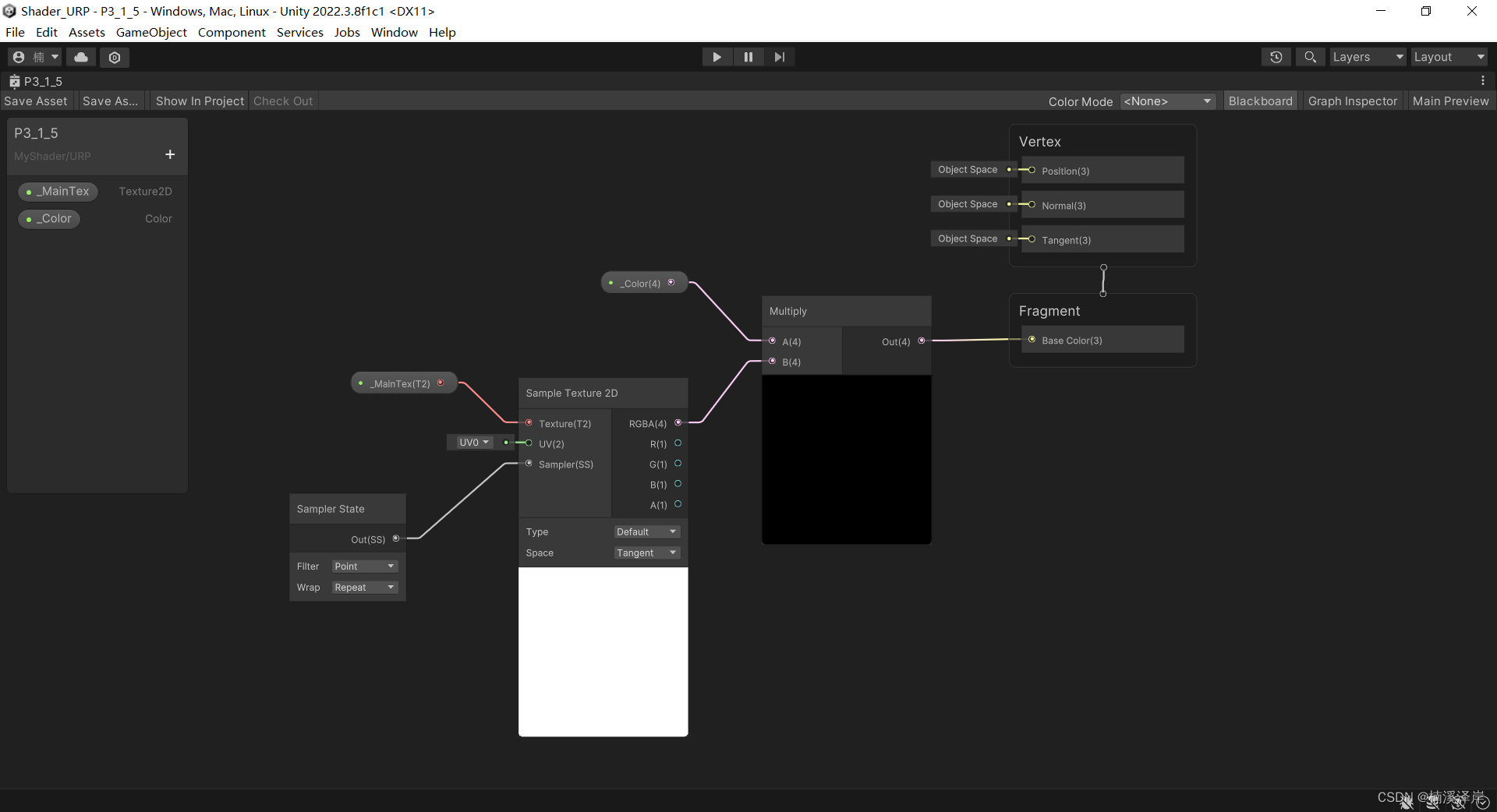
Unity中 URP Shader 的纹理与采样器的分离定义
文章目录 前言一、URP Shader 纹理采样的实现1、在属性面板定义一个2D变量用于接收纹理2、申明纹理3、申明采样器4、进行纹理采样 二、申明纹理 和 申明采样器内部干了什么1、申明纹理2、申明采样器 三、采样器设置采样器的传入格式1、纹理设置中,可以看见我们的采样…...

Electron学习第一天 ,启动项目
之前在安装官网的步骤操作,结果报错,找了好多办法,最后这种办法成功启动项目,并且没有报错,特此记录 特别提醒,最好安装淘宝镜像,npm 太慢,会导致报错问题,解决起来个人觉…...

WebService技术--随笔1
1.WebService 发展史 创建阶段(1990 年代末至 2000 年代初):在这个阶段,XML-RPC 和 SOAP 协议被引入,为跨平台和跨语言的应用程序集成提供了基础。XML-RPC 提供了一种基于 XML 的远程过程调用机制,而 SOAP…...

如何使用Docker将.Net6项目部署到Linux服务器(一)
目录 一 配置服务器环境 1.1 配置yum 1.1.1 更新yum包 1.1.2 yum命令 1.2 配置docker …...

第4章-第3节-Java中跟数组相关的几个算法以及综合应用
在写这篇博文之前,先大概说明一下,就是很常见的数组算法如求最大值、一维数组的遍历等,这里就不去专门说明了,只说一些有代表性的,然后就是冒泡排序算法很容易查阅到,这里也不专门说明了,只说明…...
AlexNet(pytorch)
AlexNet是2012年ISLVRC 2012(ImageNet Large Scale Visual Recognition Challenge)竞赛的冠军网络,分类准确率由传统的 70%提升到 80% 该网络的亮点在于: (1)首次利用 GPU 进行网络加速训练。 ÿ…...

【单调栈 】LeetCode321:拼接最大数
作者推荐 【动态规划】【广度优先搜索】LeetCode:2617 网格图中最少访问的格子数 本文涉及的知识点 单调栈 题目 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k < m n) 个数字…...

TikTok与虚拟现实的完美交融:全新娱乐时代的开启
TikTok,这个风靡全球的短视频平台,与虚拟现实(VR)技术的深度结合,为用户呈现了一场全新的娱乐盛宴。虚拟现实技术为TikTok带来了更丰富、更沉浸的用户体验,标志着全新娱乐时代的开启。本文将深入探讨TikTok…...

PXI/PCIe/VPX机箱 ARM|x86 + FPGA测试测量板卡解决方案
PXI便携式测控系统是一种基于PXI总线的便携式测试测控系统,它填补了现有台式及机架式仪器在外场测控和便携测控应用上的空白,在军工国防、航空航天、兵器电子、船舶舰载等各个领域的外场测控场合和科学试验研究场合都有广泛的应用。由于PXI便携式测控系统…...

ES6 面试题 | 12.精选 ES6 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【linux】Debian不能运行sudo的解决
一、问题: sudo: 没有找到有效的 sudoers 资源,退出 sudo: 初始化审计插件 sudoers_audit 出错 二、可用的方法: 出现 "sudo: 没有找到有效的 sudoers 资源,退出" 和 "sudo: 初始化审计插件 sudoers_audit 出错&q…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
