当前位置： 首页 > news >正文

【FPGA】分享一些FPGA协同MATLAB开发的书籍

news 2025/9/16 7:09:18

        在做FPGA工程师的这些年，买过好多书，也看过好多书，分享一下。

        后续会慢慢的补充书评。

  • 【FPGA】分享一些FPGA入门学习的书籍
  • 【FPGA】分享一些FPGA协同MATLAB开发的书籍 
  • 【FPGA】分享一些FPGA视频图像处理相关的书籍 
  • 【FPGA】分享一些FPGA高速信号处理相关的书籍 
  • 【FPGA】分享一些FPGA进阶学习的书籍 

 基于MATLAB与FPGA的图像处理教程 - 韩彬

 数字通信同步技术的MATLAB与FPGA实现——Altera/Verilog版

FPGA应用技术丛书：数字通信同步技术的MATLAB与FPGA实现

FPGA应用技术丛书：数字滤波器的MATLAB与FPGA实现（第2版）（附CD-ROM光盘1张）

正版现货 数字调制解调技术的MATLAB与FPGA实现——Altera/Verilog版

相关文章：

【FPGA】分享一些FPGA协同MATLAB开发的书籍

在做FPGA工程师的这些年，买过好多书，也看过好多书，分享一下。 后续会慢慢的补充书评。 【FPGA】分享一些FPGA入门学习的书籍【FPGA】分享一些FPGA协同MATLAB开发的书籍 【FPGA】分享一些FPGA视频图像处理相关的书籍 【FPGA】分享一些FPGA高速…...

编程日记 2023/12/25 12:17:10

幺模矩阵-线性规划的整数解特性

百度百科:幺模矩阵 在线性规划问题中，如果A为幺模矩阵，那么该问题具有最优整数解特性。也就是说使用单纯形法进行求解，得到的解即为整数解。无需再特定使用整数规划方法。 m i n c T x s . t . { A x ≥ b x ≥ 0 \begin{align*} min \quad…...

编程日记 2023/12/25 12:13:06

数据分析思维

Why&What 数据分析是为了驱动决策赋能业务。在数据分析过程中需要对目标进行拆解量化，如何拆解量化目标便是数据分析思维。 在任务拆解过程中使用的软件、统计模型、分析方法等为分析工具和手段，如何在恰当的场景合理的使用这些工具、模型、方法、手…...

编程日记 2023/12/25 12:03:58

C++ boost planner_cond_.wait(lock) 报错1225

1.如下程序段 boost unique_lock doesn’t own the mutex: Operation not permitted 问题： 其中makePlan是一个线程。这里的unlock导致错误这个报错 boost unique_lock doesn’t own the mutex: Operation not permitted bool navigation::makePlan(){ //cv::named…...

编程日记 2023/12/25 12:00:56

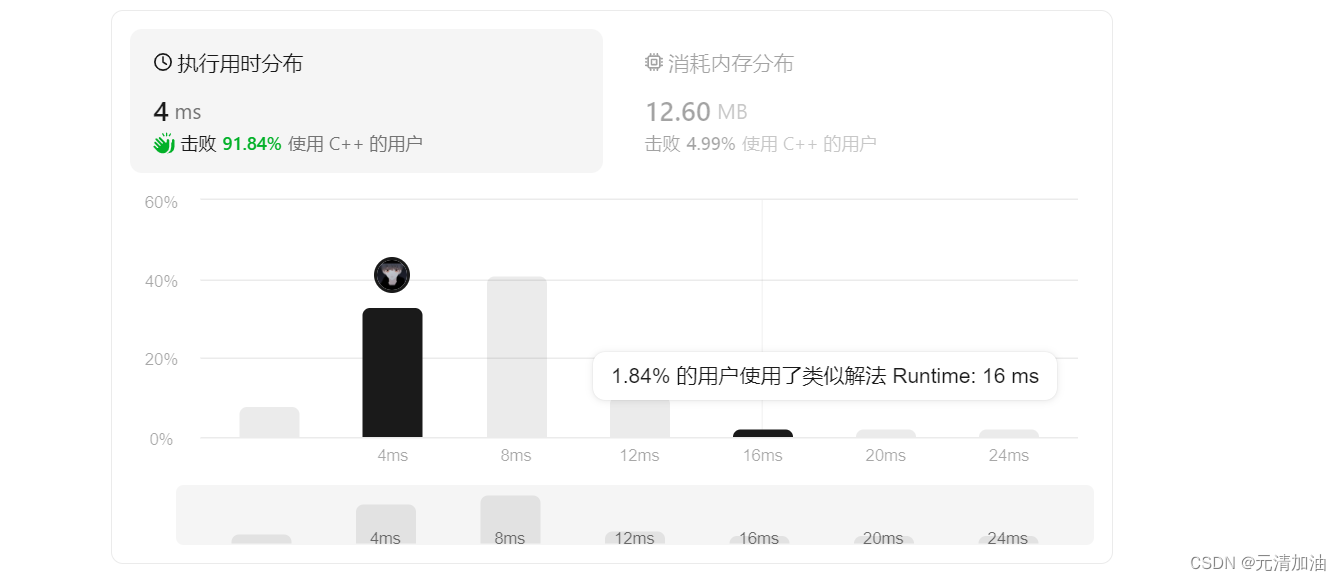
LeetCode刷题--- 字母大小写全排列

个人主页：元清加油_【C】,【C语言】,【数据结构与算法】-CSDN博客 个人专栏 力扣递归算法题 http://t.csdnimg.cn/yUl2I 【C】 http://t.csdnimg.cn/6AbpV 数据结构与算法 http://t.csdnimg.cn/hKh2l 前言：这个专栏主要讲述递归递归、搜索与回…...

编程日记 2023/12/25 11:59:55

165. 小猫爬山（DFS之剪枝与优化）

165. 小猫爬山 - AcWing题库 翰翰和达达饲养了 N 只小猫&#xff0c;这天&#xff0c;小猫们要去爬山。 经历了千辛万苦&#xff0c;小猫们终于爬上了山顶&#xff0c;但是疲倦的它们再也不想徒步走下山了&#xff08;呜咕>_<&#xff09;。 翰翰和达达只好花钱让它们…...

编程日记 2023/12/25 11:58:54

【Linux系统基础】（6）在Linux上大数据NoSQL数据库HBase集群部署、分布式内存计算Spark环境及Flink环境部署详细教程

大数据NoSQL数据库HBase集群部署 简介 HBase 是一种分布式、可扩展、支持海量数据存储的 NoSQL 数据库。 和Redis一样&#xff0c;HBase是一款KeyValue型存储的数据库。 不过和Redis设计方向不同 Redis设计为少量数据&#xff0c;超快检索HBase设计为海量数据&#xff0c;…...

编程日记 2023/12/25 11:57:53

多维时序 | MATLAB实CNN-BiGRU-Mutilhead-Attention卷积网络结合双向门控循环单元网络融合多头注意力机制多变量时间序列预测

多维时序 | MATLAB实现CNN-BiGRU-Mutilhead-Attention卷积网络结合双向门控循环单元网络融合多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实现CNN-BiGRU-Mutilhead-Attention卷积网络结合双向门控循环单元网络融合多头注意力机制多变量时间序列预测预测效果基本介…...

编程日记 2023/12/25 11:56:52

vs快捷键

ctrlMo 折叠代码块 ctrlML 打开代码块...

编程日记 2023/12/25 11:55:51

linux 内核时间计量方法

定时器中断由系统定时硬件以规律地间隔产生; 这个间隔在启动时由内核根据 HZ 值来编 程, HZ 是一个体系依赖的值, 在 <linux/param.h>中定义或者它所包含的一个子平台文 件中. 在发布的内核源码中的缺省值在真实硬件上从 50 到 1200 嘀哒每秒, 在软件模拟 器中往下到 24.…...

编程日记 2023/12/25 11:53:50

循环神经网络中的梯度消失或梯度爆炸问题产生原因分析（二）

上一篇中讨论了一般性的原则&#xff0c;这里我们具体讨论通过时间反向传播&#xff08;backpropagation through time&#xff0c;BPTT&#xff09;的细节。我们将展示目标函数对于所有模型参数的梯度计算方法。 出于简单的目的&#xff0c;我们以一个没有偏置参数的循环神经…...

编程日记 2023/12/25 11:50:47

JWT signature does not match locally computed signature

1. 问题背景 最近在协助团队小盆友调试一个验签问题&#xff0c;结果还“节外生枝”了&#xff0c;原来不是签名过程的问题&#xff0c;是token的问题。 当你看到“JWT signature does not match locally computed signature. JWT validity cannot be asserted and should not…...

编程日记 2023/12/25 11:48:45

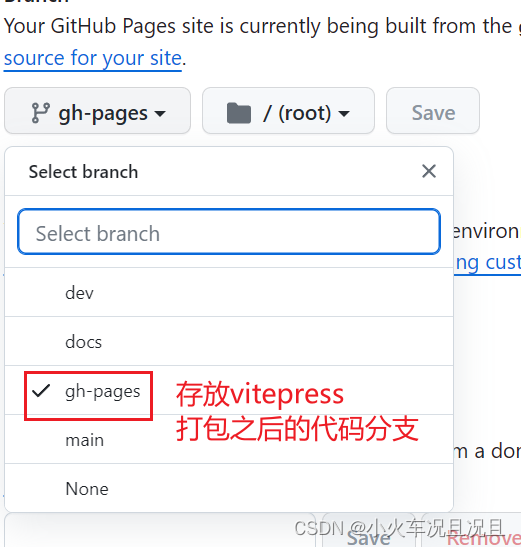
vitepress项目使用github的action自动部署到github-pages中，理论上可以通用所有

使用github的action自动部署到github-pages中 创建部署的deploy.yml文件&#xff0c;在项目的根目录下面 .github\workflows\deploy.yml 完整的代码&#xff1a;使用的是pnpm进行依赖安装。 name: 部署VitePresson:push:branches:- docs # 这段是在推送到 docs 分支时触发该…...

编程日记 2023/12/25 11:45:42

Python爬虫---解析---JSONPath

Xpath可以解析本地文件和服务器响应的文件&#xff0c;JSONPath只能解析本地文件 1. 安装jsonpath&#xff1a;pip install jsonpath 注意&#xff1a;需要安装在python解释器相同的位置,例如&#xff1a;D:\Program Files\Python3.11.4\Scripts 2. 使用步骤 2.1 导入&…...

编程日记 2023/12/25 11:44:41

路由器介绍和命令操作

先来回顾一下上次的内容&#xff1a; ip地址就是由32位二进制数组 二进位数就是只有数字0和1组成 网络位&#xff1a;类似于区号&#xff0c;表示区域作用 主机位&#xff1a;类似于号码&#xff0c;表示区域中编号 网络名称&#xff1a;网络位不变&#xff0c;主机位全为0 …...

编程日记 2023/12/25 11:43:40

Hadoop——分布式计算

一、分布式计算概述 1. 什么是计算、分布式计算？ 计算：对数据进行处理，使用统计分析等手段得到需要的结果分布式计算：多台服务器协同工作，共同完成一个计算任务2. 分布式计算常见的2种工作模式分散->汇总 （MapReduce就是这种模式）将数据分片，多台服务器各自负责一…...

编程日记 2023/12/25 11:40:37

LaTeX引用参考文献 | Texstudio引用参考文献

图片版教程&#xff1a; 文字版教程&#xff1a; ref.bib里面写参考的文献&#xff0c;ref.bib和document.tex要挨着放&#xff0c;同一个目录里面. 解析一下bib文件格式&#xff1a;aboyeji2023effect是引用文献的关键字&#xff0c;需要在正文document.tex里面使用\cite指令…...

编程日记 2023/12/25 11:39:37

如何在Go中使用模板

引言 您是否需要以格式良好的输出、文本报告或HTML页面呈现一些数据?你可以使用Go模板来做到这一点。任何Go程序都可以使用text/template或html/template包(两者都包含在Go标准库中)来整齐地显示数据。 这两个包都允许你编写文本模板并将数据传递给它们，以按你喜欢的格式呈…...

编程日记 2023/12/25 11:37:35

云原生之深入解析基于FunctionGraph在Serverless领域的FinOps的探索和实践

一、背景 Serverless 精确到毫秒级的按用付费模式使得用户不再需要为资源的空闲时间付费。然而&#xff0c;对于给定的某个应用函数&#xff0c;由于影响其计费成本的因素并不唯一&#xff0c;使得用户对函数运行期间的总计费进行精确的事先估计变成了一项困难的工作。以传统云…...

编程日记 2023/12/25 11:36:34

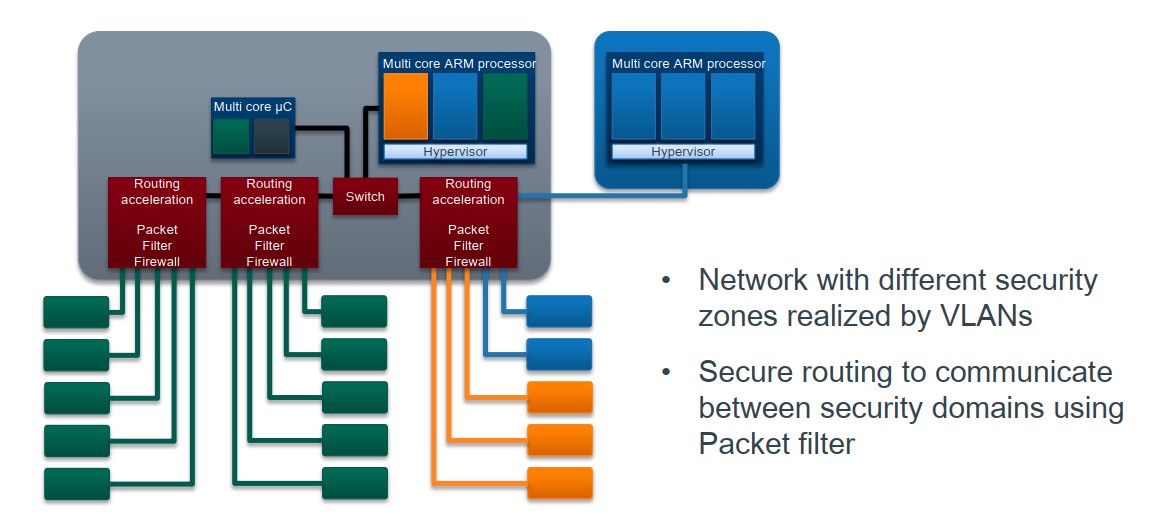
电子电器架构（E/E）演化 —— 主流主机厂域集中架构概述

电子电器架构（E/E）演化 —— 主流主机厂域集中架构概述 我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 屏蔽力是信息过载时代一个人的特殊竞争力，任何消耗你的人和事，多看一眼都是你的不对。…...

编程日记 2023/12/25 11:33:32

相机Camera日志实例分析之二：相机Camx【专业模式开启直方图拍照】单帧流程日志详解

【关注我&#xff0c;后续持续新增专题博文&#xff0c;谢谢&#xff01;&#xff01;&#xff01;】 上一篇我们讲了&#xff1a; 这一篇我们开始讲&#xff1a; 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下&#xff1a; 一、场景操作步骤 操作步…...

编程新知 2025/9/13 17:44:06

【配置 YOLOX 用于按目录分类的图片数据集】

现在的图标点选越来越多&#xff0c;如何一步解决&#xff0c;采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集&#xff08;每个目录代表一个类别&#xff0c;目录下是该类别的所有图片&#xff09;&#xff0c;你需要进行以下配置步骤&#x…...

编程新知 2025/8/25 15:23:12

C++.OpenGL （10/64）基础光照（Basic Lighting）

基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

编程新知 2025/8/30 20:41:56

Matlab | matlab常用命令总结

常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

编程新知 2025/8/11 1:05:59

代理篇12|深入理解 Vite中的Proxy接口代理配置

在前端开发中，常常会遇到 跨域请求接口 的情况。为了解决这个问题，Vite 和 Webpack 都提供了 proxy 代理功能，用于将本地开发请求转发到后端服务器。 什么是代理（proxy）？ 代理是在开发过程中，前端项目通过开发服务器，将指定的请求“转发”到真实的后端服务器，从而绕…...

编程新知 2025/9/13 13:10:12

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案

目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后&#xff0c;迭代器会失效&#xff0c;因为顺序迭代器在内存中是连续存储的&#xff0c;元素删除后&#xff0c;后续元素会前移。 但一些场景中&#xff0c;我们又需要在执行删除操作…...

编程新知 2025/9/11 23:31:22

【p2p、分布式，区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制

目录 节点的功能承载层&#xff08;GATT/Adv&#xff09;局限性&#xff1a; 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能&#xff0c;如 Configuration …...

编程新知 2025/9/14 1:29:18

嵌入式常见 CPU 架构

架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集&#xff0c;单周期执行&#xff1b;低功耗、CIP 独立外设&#xff1b;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel&#xff08;原始…...

编程新知 2025/6/10 21:24:01

前端高频面试题2：浏览器/计算机网络

本专栏相关链接 前端高频面试题1&#xff1a;HTML/CSS 前端高频面试题2&#xff1a;浏览器/计算机网络 前端高频面试题3&#xff1a;JavaScript 1.什么是强缓存、协商缓存&#xff1f; 强缓存&#xff1a; 当浏览器请求资源时&#xff0c;首先检查本地缓存是否命中。如果命…...

编程新知 2025/7/16 2:01:36

如何在Windows本机安装Python并确保与Python.NET兼容

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…...

编程新知 2025/9/13 19:26:26