C++力扣题目-- 二叉树层序遍历
- 102.二叉树的层序遍历(opens new window)
- 107.二叉树的层次遍历II(opens new window)
- 199.二叉树的右视图(opens new window)
- 637.二叉树的层平均值(opens new window)
- 429.N叉树的层序遍历(opens new window)
- 515.在每个树行中找最大值(opens new window)
- 116.填充每个节点的下一个右侧节点指针(opens new window)
- 117.填充每个节点的下一个右侧节点指针II(opens new window)
- 104.二叉树的最大深度(opens new window)
- 111.二叉树的最小深度
102思路:
我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
- 二叉树:前中后序递归法(opens new window)
- 二叉树:前中后序迭代法(opens new window)
- 二叉树:前中后序迭代方式统一写法(opens new window)
接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:

这样就实现了层序从左到右遍历二叉树。
代码如下:这份代码也可以作为二叉树层序遍历的模板,打十个就靠它了。
c++代码如下:
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}return result;}
};
107--将102的结果reverse即可;
C++代码:
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}reverse(result.begin(), result.end()); // 在这里反转一下数组即可return result;}
};199--二叉树的右视图
层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
C++代码:
class Solution {
public:vector<int> rightSideView(TreeNode* root) {vector<int>result;queue<TreeNode*>que;if (root != nullptr) { que.push(root); }while (!que.empty()){int size = que.size();for (int i = 0; i < size; i++){TreeNode* cur = que.front();que.pop();if (i == size - 1) { result.push_back(cur->val); }if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }}}return result;}
};637--二叉树的层平均值
本题就是层序遍历的时候把一层求个总和在取一个均值。
C++代码:
class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {queue<TreeNode*>que;vector<double>result;if (root != nullptr) { que.push(root); }while (!que.empty()){ int size = que.size();double sum = 0;for (int i = 0; i < size; i++){TreeNode* cur = que.front();que.pop();sum += cur->val;if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }}sum /= size;result.push_back(sum);}return result;}
};429. N 叉树的层序遍历
这道题依旧是模板题,只不过一个节点有多个孩子了
C++代码:
class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*>que;vector<vector<int>>result;if (root != nullptr) { que.push(root); }while (!que.empty()){int size = que.size();vector<int>tmp;for (int i = 0; i < size; i++){Node* cur = que.front();tmp.push_back(cur->val);que.pop();int vsize = cur->children.size();for(int j=0;j<vsize;j++){if (cur->children[j]) {que.push(cur->children[j]);}}}result.push_back(tmp);}return result;}
};515.在每个树行中找最大值
层序遍历,取每一层的最大值
C++代码:
class Solution {
public:vector<int> largestValues(TreeNode* root) {queue<TreeNode*>que;vector<int>result;if (root != nullptr) { que.push(root); }while (!que.empty()){int max = que.front()->val;int size = que.size(); for (int i = 0; i < size; i++){TreeNode* cur = que.front();if (max < (cur->val)) { max = cur->val; }que.pop();if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }}result.push_back(max);}return result;}
};116.填充每个节点的下一个右侧节点指针
思路
本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
C++代码:
class Solution {
public:Node* connect(Node* root) {queue<Node*>que;if (root != nullptr) { que.push(root); }while (!que.empty()){int size = que.size();Node* pre;Node* cur;for (int i = 0; i < size; i++){if (i == 0) {pre = que.front();que.pop();cur = pre;}else{cur = que.front();que.pop();pre->next = cur;pre = pre->next;}if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }}pre->next = nullptr;}return root;}
};117.填充每个节点的下一个右侧节点指针II
思路
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
C++代码:
class Solution {
public:Node* connect(Node* root) {queue<Node*>que;if (root != nullptr) { que.push(root); }while (!que.empty()){int size = que.size();Node* pre;Node* cur;for (int i = 0; i < size; i++){if (i == 0) {pre = que.front();que.pop();cur = pre;}else{cur = que.front();que.pop();pre->next = cur;pre = pre->next;}if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }}pre->next = nullptr;}return root;}
};104.二叉树的最大深度
思路
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
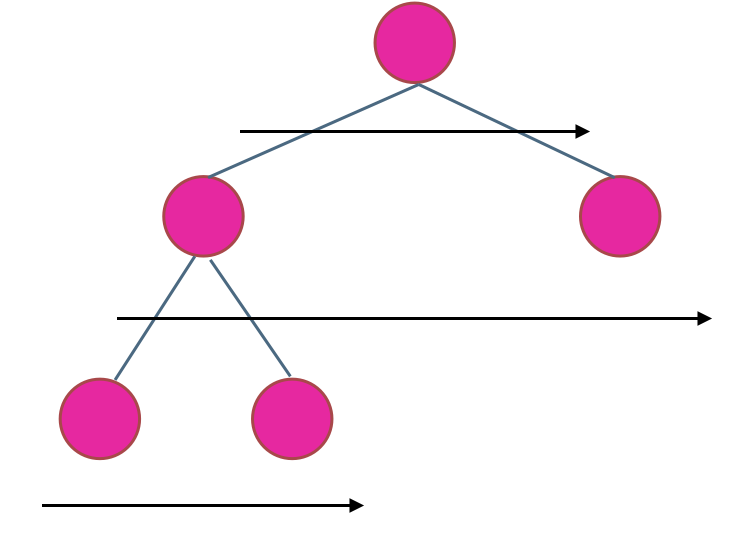
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
C++代码如下:
class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*>que;int depth = 0;if (root != nullptr) {que.push(root);}while (!que.empty()){int size = que.size();for (int i = 0; i < size; i++){TreeNode* cur = que.front();que.pop();if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }}depth++;}return depth;}
};111.二叉树的最小深度
思路
相对于 104.二叉树的最大深度 ,本题还也可以使用层序遍历的方式来解决,思路是一样的。
需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
代码如下:(详细注释)
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*>que;int depth = 0;if (root != nullptr){que.push(root);}else {return depth;} while (!que.empty()){int size = que.size();depth++;for (int i = 0; i < size; i++){TreeNode* cur = que.front();que.pop();if (cur->left) { que.push(cur->left); }if (cur->right) { que.push(cur->right); }if (cur->left == nullptr && cur->right == nullptr){return depth;}} }return depth;}
};相关文章:

C++力扣题目-- 二叉树层序遍历
102.二叉树的层序遍历(opens new window)107.二叉树的层次遍历II(opens new window)199.二叉树的右视图(opens new window)637.二叉树的层平均值(opens new window)429.N叉树的层序遍历(opens new window)515.在每个树行中找最大值(opens new window)116.填充每个节点的下一个右…...

前端实现回车键触发搜索
前端实现回车键触发搜索 前言实现方法1. html里可以用 form 来实现2. 非form中的input 前言 搜索框是个常见的功能,除了用现有的ui组件库,有的时候必须要自己封装,所以涉及到点击按钮搜索和回车搜索都要实现 实现方法 1. html里可以用 for…...

k8s yaml文件pod的生命周期
Pod是k8s中最小限额资源管理组件,也是最小化运行容器化的应用的资源管理对象。 Pod是一个抽象的概念,可以理解为一个或者多个容器化应用的集合。 在一个pod当中运行一个容器是最常用的方式。 在一个pod当中同时运行多个容器,在一个pod当中…...
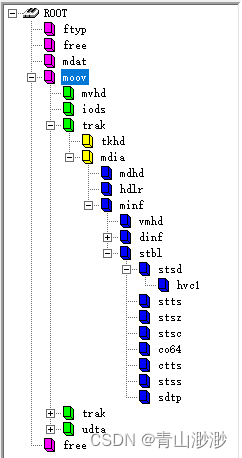
MPEG4Extractor
1、readMetaData 必须要找到 Moov box,找到 Mdat box或者 Moof box,并且创建了 ItemTable 大端 box 分为 box header 和 box content: box header由8个字节组成,前面四个字节表示这个box 的大小(包含这个头的8字节&a…...

我在工作一年时怎么都看不懂的编程写法。今天手把手教给你
作为一名程序员,你一定遇到或亲自写过这样的代码。有人将它形象的形容为shi山,或者被戏称为“面向保就业编程”。 以下面这个代码为例,其中的问题也显而易见,当越来越多的条件判断时,代码会变得非常臃肿,难…...
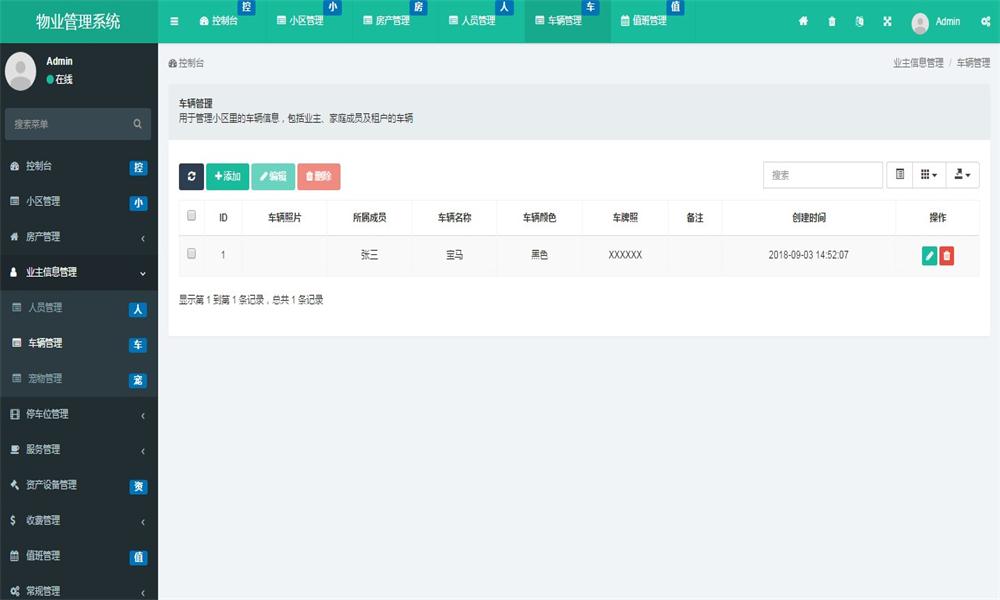
ThinkPHP5多小区物业管理系统源码(支持多小区)
基于 ThinkPHP5 Bootstrap 倾力打造的多小区物业 管理系统源码,操作简单,功能完善,用户体验良好 开发环境PHP7mysql 安装步骤: 1.新建数据库db_estate,还原数据db_estate.sql 2.修改配置文件:application/database.php 3.运…...

2024 年 API 安全:预测和趋势
随着技术以前所未有的速度不断进步,API(应用程序编程接口)安全性的复杂性也随之增加。随着 API 在现代应用程序和服务中的激增,组织将需要更好地了解其 API 环境以及 API 给运营带来的风险。 到 2024 年,预计几个关键…...

3D模型UV展开原理
今年早些时候,我为 MAKE 杂志写了一篇教程,介绍如何制作视频游戏角色的毛绒动物。 该技术采用给定的角色 3D 模型及其纹理,并以编程方式生成缝纫图案。 虽然我已经编写了一般摘要并将源代码上传到 GitHub,但我在这里编写了对使这一…...
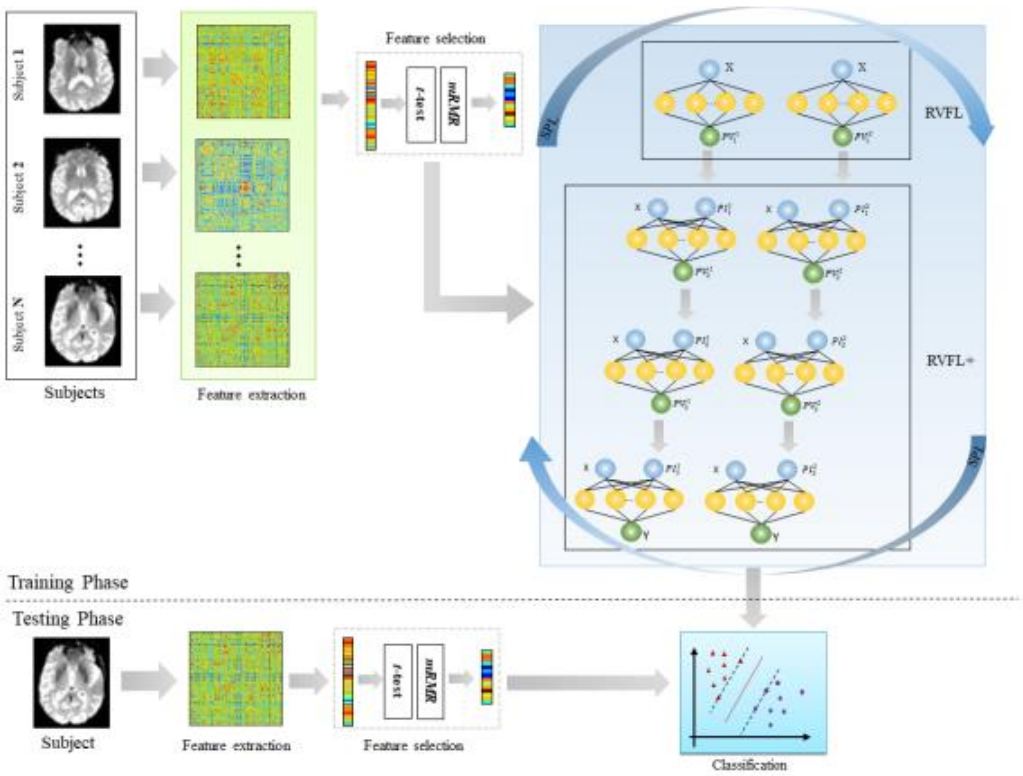
SPL-cmcRVFL+
吐槽 作者未提供代码,还有图1敢再糊点吗?...

Vue3+TS+Vite 构建自动导入开发环境
关注⬆️⬆️⬆️⬆️ 专栏后期更新更多前端内容 在一个使用 Vue 3、Vite 和 TypeScript 的项目中,配置 unplugin-auto-import 和 unplugin-vue-components 插件可以极大地提高开发效率,因为它们可以自动导入 Vue 相关的 API 和 Vue 组件,从而减少了手动导入的需要。 文章目…...
长期使用外接键盘,外物压着自带键盘,容易导致华硕飞行堡垒FX53VD键盘全部失灵【除电源键】
华硕飞行堡垒FX53VD键盘全部失灵【除电源键】 前言一、故障排查二、发现问题三、使用方法总结 前言 版本型号: 型号 ASUS FX53VD(华硕-飞行堡垒) 板号:GL553VD 故障情况描述: 键盘无法使用,键盘除开机键外…...

JavaScript-循环嵌套断点调试-笔记
1.do...while循环 do while语法结构: 循环初始值; do{ //代码; 增量; }while(循环条件); <script> // 输出十句 : 你好世界 var …...
1042: 数列求和3 和 1057: 素数判定 和 1063: 最大公约与最小公倍
1042: 数列求和3 题目描述 求1-2/33/5-4/75/9-6/11...的前n项和,结果保留3位小数。 输入 输入正整数n(n>0)。 输出 输出一个实数,保留3位小数,单独占一行。 样例输入 5 样例输出 0.917 #include<stdio.h> int main(){in…...

[足式机器人]Part2 Dr. CAN学习笔记-动态系统建模与分析 Ch02-8 Bode Plot伯德图
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-动态系统建模与分析 Ch02-8 Bode Plot伯德图 Bode Plot 手绘技巧与应用...
Java 将Excel转换为TXT文本格式
TXT文件是一种非常简单、通用且易于处理的文本格式。在处理大规模数据时,将Excel转为TXT纯文本文件可以提高处理效率。此外,许多编程语言和数据处理工具都有内置的函数和库来读取和处理TXT文件,因此将Excel文件转换为TXT还可以简化数据导入过…...

什么事“网络水军”?他们的违法活动主要有四种形式
我国治理网络水军,包括造谣引流、舆情敲诈、刷量控评、有偿删帖等各类“网络水军”等违法犯罪活动已经许久。 日前,官方召开新闻发布会,公布了相关的一些案件进程,今年已累计侦办相关案件339起,超过历年的全年侦办案件…...
)
授权策略(authorize方法)
authorize方法(授权策略的使用示例) $this->authorize(destroy, $status) 要实现这个功能,你需要执行以下步骤: 1、创建一个授权策略: 在Laravel中,授权策略是用于定义用户对特定操作的权限的类。你可…...
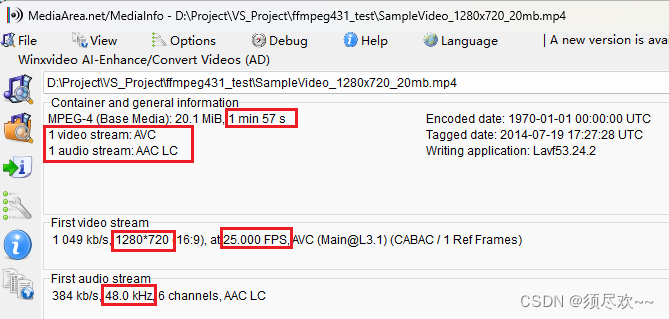
FFmpeg获取音视频流信息
文章目录 前言一、需求二、源码三、运行结果 前言 本文记录用 FFmpeg 获取视频流音频流的信息(编码格式、分辨率、帧率、播放时长…),所用的工程基于上个博客编译成功的工程:使用FFmpeg4.3.1的SDK官方开发包编译ffmpeg.c 一、需求…...

编程语言的走向又将如何呢?
编程语言的未来? 随着科技的飞速发展,编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心,为程序员提供了与机器沟通的桥梁。那么,在技术不断进步的未来,编程语言的走向又将如何呢? 1. 更…...

基于SpringBoot的电影评论网站
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的电影评论网站,java项目…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
