算法训练营第四十二天|动态规划:01背包理论基础 416. 分割等和子集
目录
- 动态规划:01背包理论基础
- 416. 分割等和子集
动态规划:01背包理论基础
文章链接:代码随想录
题目链接:卡码网:46. 携带研究材料
01背包问题
二维数组解法:
#include <bits/stdc++.h>
using namespace std;void slove(int M, int N){vector<vector<int>> dp(M, vector<int> (N + 1));vector<int> weight(M), value(M);for (int i = 0; i < M; i++){cin >> weight[i];}for (int i = 0; i < M; i++){cin >> value[i];}for (int j = 0; j <= N; j++){if (j >= weight[0]) dp[0][j] = value[0];}for (int i = 1; i < M; i++){for (int j = 0; j <= N; j++){if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}cout << dp[M - 1][N] << endl;
}int main(){int M, N;cin >> M >> N;slove(M, N);return 0;
}
思路:就是按代码随想录上的那张二维表来看,更新 j 重量下的背包能放0 - i 中多少最大价值的物品;然后一行一行的更新,更新到新物品时,要么就是在 j 重量下放不下,也就是
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
要么能放下就取 原来 或者 新更新物品后背包中的最大值,也就是
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其中,
dp[i - 1][j]
代表不放入 i 物品
dp[i - 1][j - weight[i]] + value[i]
代表在 j 重量下先空出weight[i]这么大的空间,然后再放如 i 物品,它可能是本来就有这么大空间,也可能是把其它一些物品拿出去后再放入的 i 物品。
一维(滚动数组)数组解法:
#include <bits/stdc++.h>
using namespace std;void slove(int M, int N){vector<int> dp(N + 1, 0);vector<int> weight(M), value(M);for (int i = 0; i < M; i++){cin >> weight[i];}for (int i = 0; i < M; i++){cin >> value[i];}for (int i = 0; i < M; i++){for (int j = N; j >= weight[i]; j--){dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[N] << endl;
}int main(){int M, N;cin >> M >> N;slove(M, N);return 0;
}
一维数组相比二维数组解法就是将每次更新都放在一行上,而且省去了初始化,所以会节省很多空间,这点在后面 leetcode 上的那题会看到比较。另外要注意在遍历重量时是倒序遍历的:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
正序遍历会引起重复,而二维数组不会重复是因为每行都用的是上一行的值来更新的。
第一天理解的时候迷迷糊糊,第二天没事时有想了一会突然茅塞顿开了哈哈哈。
416. 分割等和子集
文章链接:代码随想录
题目链接:416. 分割等和子集
思路:01背包应用问题,留足背包的容量,也就是最大总和的一半值加一,如果更新到最后在半值重量的背包中能正好装满,就说明数组可以对半分。
二维数组解法:
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for (int i : nums){sum += i;}if (sum % 2 == 1) return false;int target = sum / 2;vector<vector<int>> dp(nums.size(), vector<int> (10001));for (int j = 0; j < 10001; j++){if (j >= nums[0]) dp[0][j] = nums[0];}for (int i = 1; i < nums.size(); i++){for (int j = 0; j < 10001; j++){if (j < nums[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);}}if (dp[nums.size() - 1][target] == target) return true;return false;}
};
一维(滚动)数组解法:
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for (int i : nums){sum += i;}if (sum % 2 == 1) return false;int target = sum / 2;vector<vector<int>> dp(nums.size(), vector<int> (10001));for (int j = 0; j < 10001; j++){if (j >= nums[0]) dp[0][j] = nums[0];}for (int i = 1; i < nums.size(); i++){for (int j = 0; j < 10001; j++){if (j < nums[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);}}if (dp[nums.size() - 1][target] == target) return true;return false;}
};

这里可以看出两种解法的时间空间对比,显然二维解法有着更大的时间和空间复杂度。因此以后的应用问题尽可能一维(滚动)数组解法。
第四十二天补卡,这两天回学校吃组饭,又耽误了两天,后面那顿饭你不行不去吃了;大体知识能串联起来了,今天开始撸项目背八股,哪不会学哪了,单学效率太低了,争取能在春节后找到个实习,加油!!!
相关文章:

算法训练营第四十二天|动态规划:01背包理论基础 416. 分割等和子集
目录 动态规划:01背包理论基础416. 分割等和子集 动态规划:01背包理论基础 文章链接:代码随想录 题目链接:卡码网:46. 携带研究材料 01背包问题 二维数组解法: #include <bits/stdc.h> using namesp…...

前端 JS篇快问快答
问题:常见的特殊字符(不包括空格\s) 正则表达式为: 回答:/[!#$%^&*()\-_{};:",.<>/?[\]~|]/ (加粗的紫色字符都是特殊字符) 问题:常见的特殊字符(包括…...

vue/vue3/js来动态修改我们的界面浏览器上面的文字和图标
前言: 整理vue/vue3项目中修改界面浏览器上面的文字和图标的方法。 效果: vue2/vue3: 默认修改 public/index.html index.html <!DOCTYPE html> <html lang"en"><head><link rel"icon" type"image/sv…...

MobaXterm SSH 免密登录配置
文章目录 1.简介2.SSH 免密登录配置第一步:点击 Session第二步:选择 SSH第三步:输入服务器地址与用户名第四步:设置会话名称第五步:点击 OK 并输入密码 3.密码管理4.小结参考文献 1.简介 MobaXterm 是一个功能强大的终…...

霍兰德职业兴趣测试:找到与你性格匹配的职业
霍兰德职业兴趣理论 约翰霍兰德(John Holland)是美国约翰霍普金斯大学心理学教授,美国著名的职业指导专家。他于1959年提出了具有广泛社会影响的职业兴趣理论。认为人的人格类型、兴趣与职业密切相关,兴趣是人们活动的巨大动力&a…...

LVGL学习笔记 显示和隐藏 对象的属性标志位 配置
在显示GUI的过程中需要对某些对象进行临时隐藏或临时显示,因此需要对该对象的FLAG进行配置就可以实现对象的显示和隐藏了. 调用如下接口可以实现: lv_obj_add_flag(user_obj, LV_OBJ_FLAG_HIDDEN);//隐藏对象lv_obj_clear_flag(user_obj, LV_OBJ_FLAG_HIDDEN);//取消隐藏实现的…...

cuda上使用remap函数
在使用opencv中的remap函数时,发现运行时间太长了,如果使用视频流进行重映射时根本不能实时,因此只能加速 1.使用opencv里的cv::cuda::remap函数 cv::cuda::remap函数头文件是#include <opencv2/cudawarping.hpp>,编译ope…...
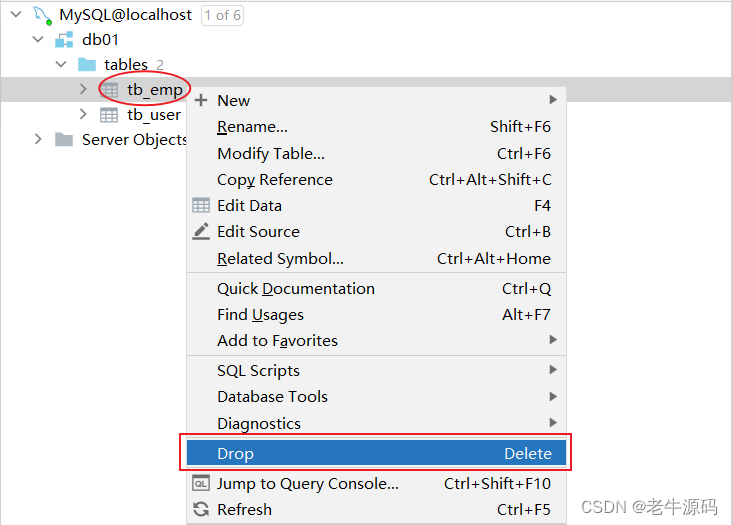
【JaveWeb教程】(18) MySQL数据库开发之 MySQL数据库设计-DDL 如何查询、创建、使用、删除数据库数据表 详细代码示例讲解
目录 2. 数据库设计-DDL2.1 项目开发流程2.2 数据库操作2.2.1 查询数据库2.2.2 创建数据库2.2.3 使用数据库2.2.4 删除数据库 2.3 图形化工具2.3.1 介绍2.3.2 安装2.3.3 使用2.2.3.1 连接数据库2.2.3.2 操作数据库 2.3 表操作2.3.1 创建2.3.1.1 语法2.3.1.2 约束2.3.1.3 数据类…...

ElasticSearch学习笔记-SpringBoot整合Elasticsearch7
项目最近需要接入Elasticsearch7,顺带记录下笔记。 Elasticsearch依赖包版本 <properties><elasticsearch.version>7.9.3</elasticsearch.version><elasticsearch.rest.version>7.9.3</elasticsearch.rest.version> </propertie…...

[足式机器人]Part2 Dr. CAN学习笔记 - Ch02动态系统建模与分析
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记 - Ch02动态系统建模与分析 1. 课程介绍2. 电路系统建模、基尔霍夫定律3. 流体系统建模4. 拉普拉斯变换(Laplace)传递函数、微分方程4.1 Laplace Transform 拉式变换4.2 收…...

【一周年创作总结】人生是远方的无尽旷野呀
那一眼瞥见的伟大的灵魂,却似模糊的你和我 文章目录 📒各个阶段的experience🔎大一寒假🔎大一下学期🔎大一暑假🔎大二上学期(现在) 🍔相遇CSDN🛸自媒体&#…...

金融帝国实验室(Capitalism Lab)V10版本游戏平衡性优化与改进
即将推出的V10版本中的各种游戏平衡性优化与改进: ————————————— 一、当玩家被提议收购一家即将破产的公司时,显示商业秘密。 当一家公司濒临破产,玩家被提议收购该公司时,如果玩家有兴趣评估该公司,则无…...

[SpringBoot]接口的多实现:选择性注入SpringBoot接口的实现类
最近在项目中遇到两种情况,准备写个博客记录一下。 情况说明:Service层一个接口是否可以存在多个具体实现,此时应该如何调用Service(的具体实现)? 其实之前的项目中也遇到过这种情况,只不过我采…...

北京大学 wlw机器学习2022春季期末试题分析
北京大学 wlw机器学习2022春季期末试题分析 前言新的开始第一题第二题第三题 前言 你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。 新的开始 第…...
)
前端文件下载方法(包含get和post)
export const downloadFileWithIframe (url, name) > {const iframe document.createElement(iframe);iframe.style.display none; // 防止影响页面iframe.style.height 0; // 防止影响页面iframe.name name;iframe.src url;document.body.appendChild(iframe); // 这…...
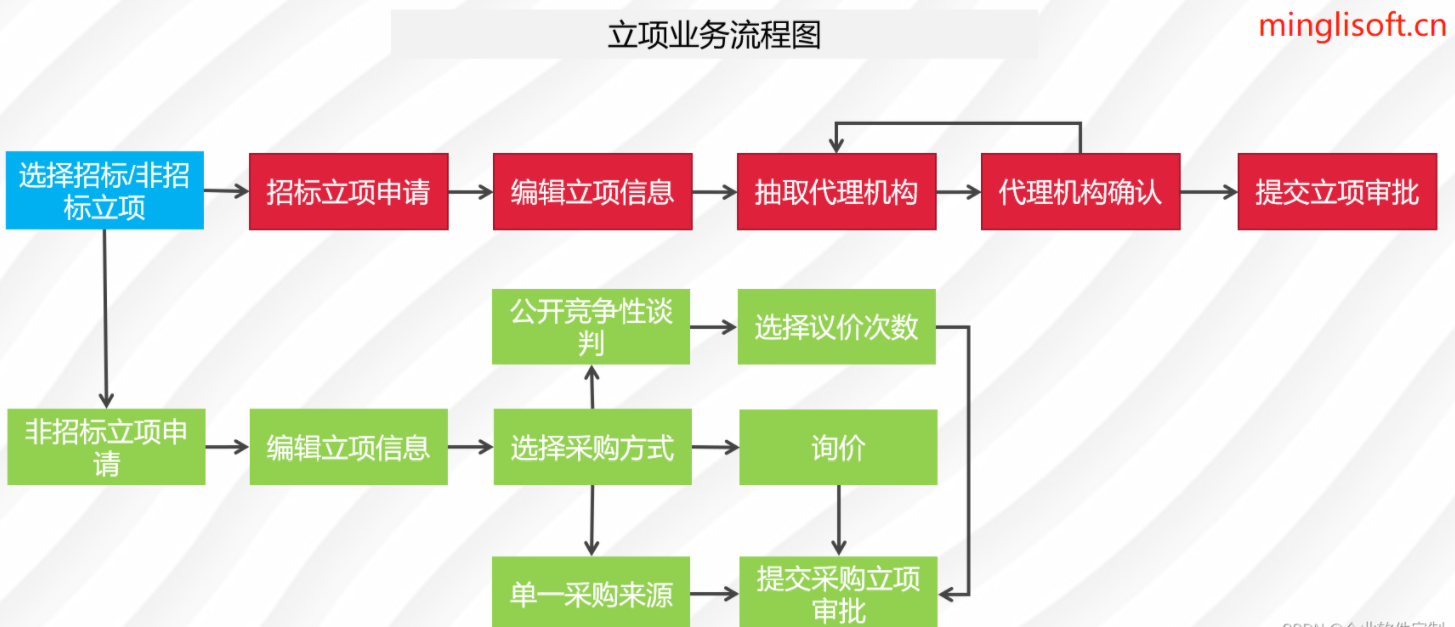
高性能、可扩展、支持二次开发的企业电子招标采购系统源码
在数字化时代,企业需要借助先进的数字化技术来提高工程管理效率和质量。招投标管理系统作为企业内部业务项目管理的重要应用平台,涵盖了门户管理、立项管理、采购项目管理、采购公告管理、考核管理、报表管理、评审管理、企业管理、采购管理和系统管理等…...

2645. 构造有效字符串的最少插入数
Problem: 2645. 构造有效字符串的最少插入数 文章目录 解题思路解决方法复杂度分析代码实现 解题思路 解决此问题需要确定如何以最小的插入次数构造一个有效的字符串。首先,我们需要确定开头的差距,然后决定中间的补足,最后决定末尾的差距。…...
C#,快速排序算法(Quick Sort)的非递归实现与数据可视化
排序算法是编程的基础。 常见的四种排序算法是:简单选择排序、冒泡排序、插入排序和快速排序。其中的快速排序的优势明显,一般使用递归方式实现,但遇到数据量大的情况则无法适用。实际工程中一般使用“非递归”方式实现。 快速排序(Quick Sor…...

【操作系统xv6】学习记录2 -RISC-V Architecture
说明:看完这节,不会让你称为汇编程序员,知识操作系统的前置。 ref:https://binhack.readthedocs.io/zh/latest/assembly/mips.html https://www.bilibili.com/video/BV1w94y1a7i8/?p7 MIPS MIPS的意思是 “无内部互锁流水级的微…...
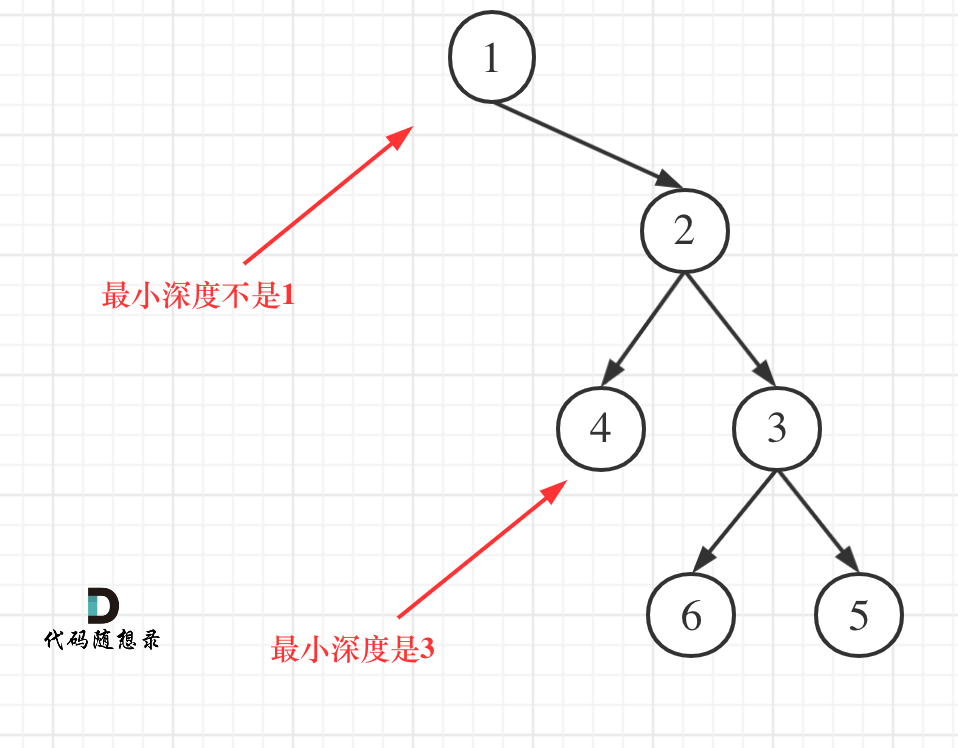
C++力扣题目111--二叉树的最小深度
力扣题目链接(opens new window) 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明: 叶子节点是指没有子节点的节点。 示例: 给定二叉树 [3,9,20,null,null,15,7], 返回它的最小深度 2 思路 看完了这篇104.二…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
