理解Herbrand Equivalence
笔者最近在看GVN的一系列论文,总会看到一个概念叫Herbran Equivalence,依靠这种定义,能够判断一个GVN算法是否是complete的,也即检测一个算法是否是precise的,只有找到所有Herbrand Equivalence关系的算法才能称得上是完全的。
目录
- 理解:程序表达式之间的等值关系是不可判定的
- phi结点和普通表达式之间的相等性
- 《一种高效的完全值编号算法》定义的值编号
- 定义Herbrand等值关系
- 定义值编号
- 算法执行
理解:程序表达式之间的等值关系是不可判定的
由于检测程序表达式间一般的等值关系是不可判定的,大部分 GVN 算法都将问题做了简化,通常假设条件语句的结果在编译期间是不确定的,并且对所有的运算符都不考虑其特殊语义,即忽略它们可能满足的特殊运算法则,将不同结构的表达式看作不同的表达式. 满足这些限制条件的表达式间的等值关系被称作 Herbrand 等值关系.能够检测到程序中全部 Herbrand 等值关系的 GVN 算法被称为完全 GVN 算法.
以上内容摘自《一种高效的完全值编号算法》。
两个程序表达式是否是等值的,这个问题在编译是无法判定,例如表达式a + b 和 a * b,表面看起来二者不是相等的,但是当运行时赋值a = 2, b = 2,此时两个表达式就是相等的。假定条件表达式在编译期不确定,前提是条件表达式的值不能通过静态分析得到,也即phi结点的两个分支执行哪个是不确定的。所有的运算符不考虑特殊语义,结合下文是说不考虑两个不同运算结构之间的等价性。
phi结点和普通表达式之间的相等性
这篇论文中还举了一些算法之所以是不完全的例子——也即他们无法发现phi结点和普通表达式之间的相等性。
以下几个例子实现了论文中的几个例子。
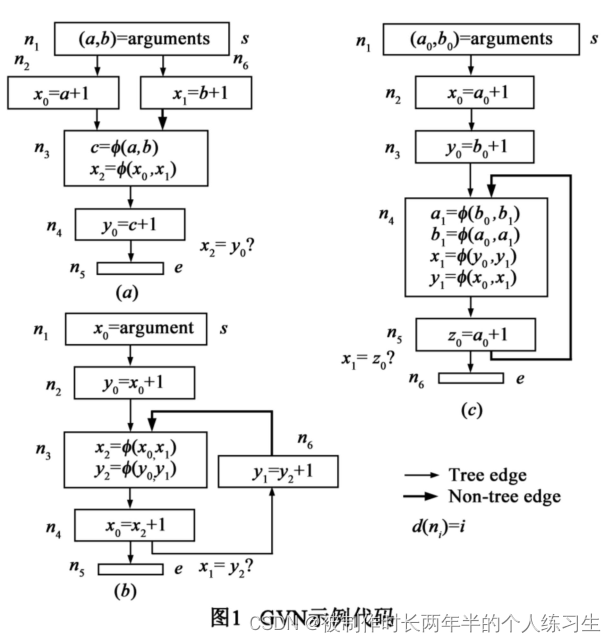
例子1:在input例子中发现两个表达式x和y的相等性,在LLVM 中可以识别到此两个表达式之间的相似性并删除之。贴一个Compiler Explorer的链接。
#include <stdio.h>int input(int a, int b) {int c, d, e, x, y, z;scanf("%d", &d);if(d) {x = a + 1;c = a;} else {x = b + 1;c = b;}y = c + 1;scanf("%d", &e);if(e) {return x;} else {return y;}
}int main()
{int a, b;scanf("%d %d", &a, &b);input(a, b);
}
生成的IR主要部分如下:
%0 = load i32, ptr %d, align 4%tobool.not = icmp eq i32 %0, 0%b.a = select i1 %tobool.not, i32 %b, i32 %a%retval.0 = add nsw i32 %b.a, 1ret i32 %retval.0
突然发现,论文给出了例子2是有问题的。
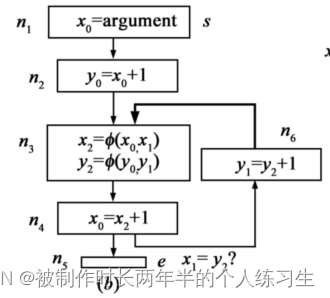
这里使用的标记方法是先将 ϕ \phi ϕ结点的所有分支标记完再标记 ϕ \phi ϕ结点,这本身并没有问题,问题在于 n 4 n_4 n4中的表达式应该为 x 1 = x 2 + 1 x_1 = x_2 + 1 x1=x2+1。
在修改之后的情况下,当 n 4 n_4 n4基本块的结尾到 n 5 n_5 n5基本块或是 n 4 n_4 n4基本块的结尾到 n 3 n_3 n3基本块的开始都是满足 x 1 = y 2 x_1=y_2 x1=y2的情况的,但是在 n 3 n_3 n3到 n 4 n_4 n4结尾这部分是不满足上述等值关系的。因此此种情况可以将两者标记为等值表达式但需要注意范围,不能贸然消除。
例子2对应的Compiler Explorer链接。
例子2:
#include <stdio.h>
int z;
int input(int x, int e, int f) {int y;y = x + 1;do {// if (x == y) {// z = 1;// } else {// z = 0;// }x++;// if (x == y) {// z = 1;// } else {// z = 0;// }if (e++ > 0) {break;} else {y++;}} while (1);return 0;
}int main() {int x, e, f;scanf("%d %d %d", &x, &e, &f);return input(x, e, f);
}
为了尽量凸显对该GVN能否正确识别,我修改了原文的例子以更好的阐述笔者的思想,读者可以自己尝试,当第一处注释打开时,编译器会判定两个表达式不相等,因此将全局变量z设置为0,第二处注释打开时,编译器会判定两个表达式相等,将全局变量设置为1.对应上图中x1和y1不相等,但x1和y2相等。
第三个例子不能用LLVM实现,因为LLVM不存在两个phi结点的依赖关系。也即图中 a 1 a_1 a1和 b 1 b_1 b1之间存在着矛盾关系。
根据论文后续的描述也说明了上述例子在SSA中不成立。相关描述如下:
本文中的模型和算法都基于静态单赋值形式的程序. 在一个静态单赋值形式的程序中,所有变量都有唯一的定值语句,并且所有对变量的使用都被该变量的定值语句所支配,即从程序的入口到达对该变量的使用的所有执行路径都一定经过该变量的定值语句.
可以看到,在上述例子中b1的第一次使用并没有经过其定值。
《一种高效的完全值编号算法》定义的值编号
论文的第二和第三部分分别给出了Herbrand等值关系和值编号的定义。
定义Herbrand等值关系
首先来看第二部分。
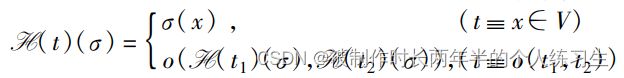
此公式首先定义了某个值到一个表达式的定义,作者的思路是将所有的值都上溯到定义他们的表达式的形式,这样可以比较不同值之间的相等性,带着这样的想法再来看上述公式,第一种情况是t=x的形式(根据后文的描述称为变量表达式),直接将x的表达式传递给t,第二种是t = t1 o t2的二元表达式形式(根据后文的描述称为包含运算符的表达式),将两个二元表达式的操作数的定义进行二元计算。
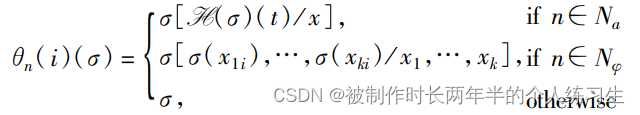
其后作者又定义了一个转换函数,也即经过一个程序节点(语句)之后表达式集合的变化,第一种可能是赋值语句,直接将表达式中的t换成x。如果是phi结点,将每条分支上的都进行转换。
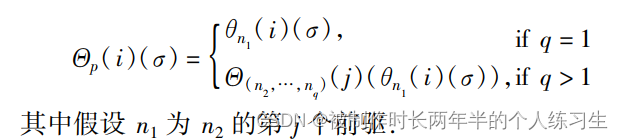
有了单个节点的处理方式,就能够得到一条路径的处理方式,无外乎将不同节点之间的转换函数连接,当遇到phi节点时,当路径明确的情况下也就能选择出某个分支。

基于上述公式给出了一个P-Herbrand关系,这里的P是Partial的简写,突出了当前路径只是一种可能的运行情况。这个公式定义的不清晰,根据下文的描述应该是检测了某个路径下的Herbrand等值关系。
最后一句话是说当P是所有路径的集合时,得到的Herbrand等值关系不再是部分的,所以可以省略前缀P-。
定义值编号
值编号定义前,作者先定义了两个值编号之间的比较,有如下公式。
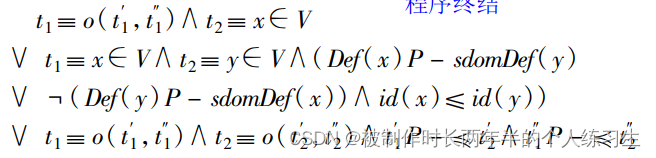
集合原文的描述更容易理解,这里我只说一个问题,第三行两个表达式写反了,应该是第二行最后一部分的否定,否则第二行和第三行不能构成一个分支上的完备集。

上述定义很明显,如果有变量表达式,那么从其等值集合中取一个最小的表达式作为当前变量的值编号,如果一个表达式是运算符表达式,取最小两个表达式的运算结果作为值编号。
算法执行
这一部分可以结合原文的例子来看,更好理解。
相关文章:

理解Herbrand Equivalence
笔者最近在看GVN的一系列论文,总会看到一个概念叫Herbran Equivalence,依靠这种定义,能够判断一个GVN算法是否是complete的,也即检测一个算法是否是precise的,只有找到所有Herbrand Equivalence关系的算法才能称得上是…...

【SimPy系列博客之官方example学习与解读】—— Example 3: Car Wash
Hello,CSDN的各位小伙伴们,又见面啦!今天我们要学习的例程是:Car Wash!我们开始吧! 例程背景 这个例程相对于example 2来说会简单一些,有一个洗车厂,里面有若干台洗车机器…...

前端随机验证码安全验证sdk
前端随机验证码安全验证sdk 前言介绍一、效果展示二、使用步骤1.引入库2.参数说明3.方法与事件说明4.如何通过API获取当前用户的验证状态 前端必备工具推荐网站(免费图床、API和ChatAI等实用工具): http://luckycola.com.cn/ 前言 验证码:是一种校验区分用户是…...
语境化语言表示模型
一.语境化语言表示模型介绍 语境化语言表示模型(Contextualized Language Representation Models)是一类在自然语言处理领域中取得显著成功的模型,其主要特点是能够根据上下文动态地学习词汇和短语的表示。这些模型利用了上下文信息…...

PDO【配置】
PDOr: 6040 控制字 6060 模式 6083 加速度 6084 减速度 =====================【定位1】:// 补间7 607A 定位位置 6081 定位速度 =====================【速度3】: 60FF 目标速度 =====================【力矩4…...

CMake入门教程【高级篇】管理MSVC编译器警告
😈「CSDN主页」:传送门 😈「Bilibil首页」:传送门 😈「动动你的小手」:点赞👍收藏⭐️评论📝 文章目录 1.什么是MSVC?2.常用的屏蔽警告3.MSVC所有警告4.target_compile_options用法5.如何在CMake中消除MSVC的警告?6.屏蔽警告编写技巧...
【JaveWeb教程】(8)Web前端基础:Vue组件库Element之Table表格组件和Pagination分页组件 详细示例介绍
目录 1 Table表格组件1.1 组件演示1.2 组件属性详解 2 Pagination分页2.1 组件演示2.2 组件属性详解2.3 组件事件详解 接下来我们来学习一下ElementUI的常用组件,对于组件的学习比较简单,我们只需要参考官方提供的代码,然后复制粘贴即可。本节…...

llama_index 创始人为我们展示召回提升策略(提升15%)
用句子向量替换为句子向量 句子检索,将句子转化为向量。在检索的过程中,假如句子命中,则将句子周围的内容也当做检索内容。 对比句子检索和之前的按块去做切分的检索。可以看到,内容的相关性提升了8%, 构建数据的时候…...
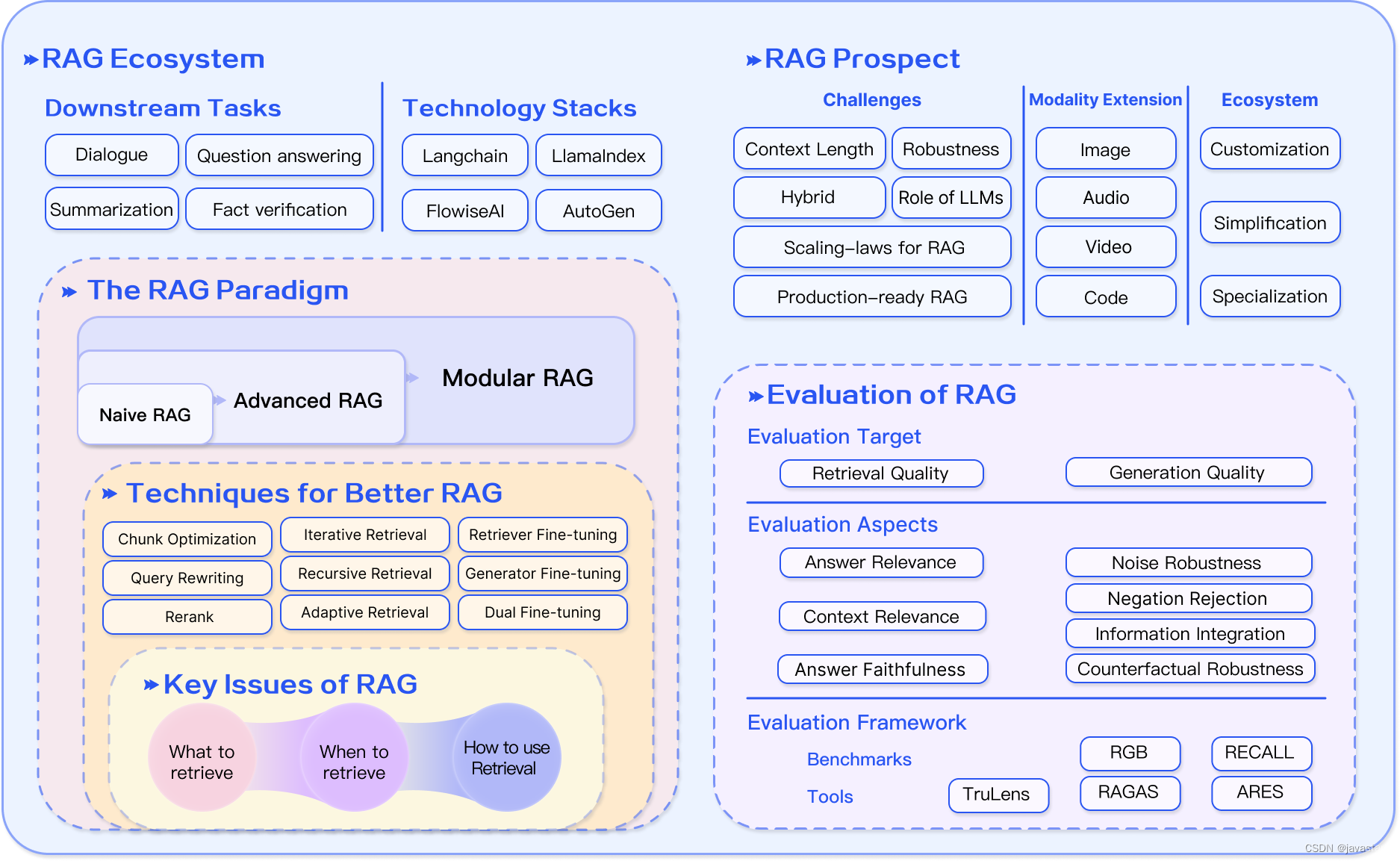
RAG 详解
原文:GitHub - Tongji-KGLLM/RAG-Survey 目录 RAG调查 什么是RAG?RAG的范式 幼稚的 RAG高级 RAG模块化 RAG如何进行增强?RAG 还是微调?如何评估 RAG?前景 严峻的挑战多式联运扩展RAG的生态系统RAG论文清单 增强阶段 …...

【llm 部署运行videochat--完整教程】
# 申请llama权重 https://ai.meta.com/resources/models-and-libraries/llama-downloads/ -> 勾选三个模型 -> 等待接收右键信息 # 下载llama代码库 git clone https://github.com/facebookresearch/llama.git cd llama bash download.py -> email -> url …...

Talking about likes
Tutorial Hi! Tim here with another 925English lesson! In today’s lesson, we’re learning how to talk about likes and preferences. Why It’s Important: Talking about things we like is common in various situations, from meetings to casual chats over lunch…...

DeepSeek 发布全新开源大模型,数学推理能力超越 LLaMA-2
自从 LLaMA 被提出以来,开源大型语言模型(LLM)的快速发展就引起了广泛研究关注,随后的一些研究就主要集中于训练固定大小和高质量的模型,但这往往忽略了对 LLM 缩放规律的深入探索。 开源 LLM 的缩放研究可以促使 LLM…...
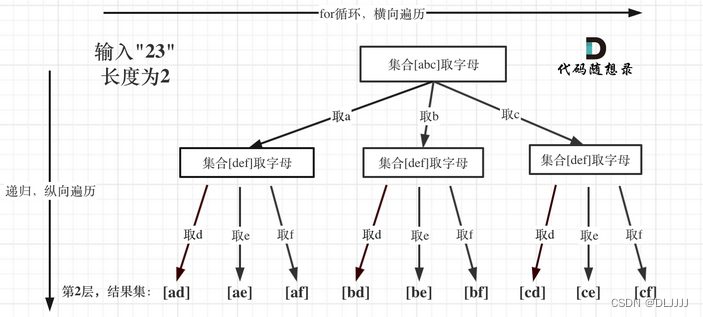
代码随想录算法训练营第二十一天| 回溯 216. 组合总和 III 17. 电话号码的字母组合
216. 组合总和 III 可以参考77.组合中关于选取数组的相关操作。 递归函数的返回值以及参数:一般为void类型 递归函数终止条件:path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,然后当n为0的时候࿰…...
微服务架构最佳实践
我的新书《Android App开发入门与实战》已于2020年8月由人民邮电出版社出版,欢迎购买。点击进入详情 构建和管理微服务是一项艰巨的任务。这是因为微服务就像多个并行的整体应用程序,它们都必须处于同步通信和并发运行时间。因此,在设计和构建…...

国内首款支持苹果Find My芯片-伦茨科技ST17H6x
深圳市伦茨科技有限公司(以下简称“伦茨科技”)发布ST17H6x Soc平台。成为继Nordic之后全球第二家取得Apple Find My「查找」认证的芯片厂家,该平台提供可通过Apple Find My认证的Apple查找(Find My)功能集成解决方案。…...
linux 01 centos镜像下载,服务器,vmware模拟服务器
https://www.bilibili.com/video/BV1pz4y1D73n?p3&vd_source4ba64cb9b5f8c56f1545096dfddf8822 01.使用的版本 国内主要使用的版本是centos 02.centos镜像下载 这里的是centos7 一.阿里云官网地址:https://www.aliyun.com/ 二. -----【文档与社区】 —【…...
)
Linux安装RabbitMq明白纸(无图)
Linux安装RabbitMq步骤 安装环境Erlang和RabbitMQ版本对照安装包下载地址登录Linux服务器创建安装目录将之前下载的两个rpm文件上传到这个目录下,并解压安装Erlang安装完成后,查看Erlang版本安装socat(RabbitMq安装需要这个)解压并…...
Android - CrashHandler 全局异常捕获器
官网介绍如下:Thread.UncaughtExceptionHandler (Java Platform SE 8 ) 用于线程因未捕获异常而突然终止时调用的处理程序接口。当线程由于未捕获异常而即将终止时,Java虚拟机将使用thread . getuncaughtexceptionhandler()查询该线程的UncaughtExceptio…...

商品源数据如何采集,您知道吗?
如今,电子商务已经渗透到了人们生活的方方面面。2020年新冠肺炎突如其来,打乱了人们正常的生产生活秩序,给经济发展带来了极大的影响。抗击疫情过程中,为避免人员接触和聚集,以“无接触配送”为营销卖点的电子商务迅速…...
输入输出流、字符字节流、NIO
1、对输入输出流、字符字节流的学习,以之前做的批量下载功能为例 批量下载指的是,将多个文件打包到zip文件中,然后下载该zip文件。 1.1下载网络上的文件 代码参考如下: import java.io.*; import java.net.URL; import java.n…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
