Java 二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问依次且仅被访问一次。
前序遍历(根 左 右)
先访问根结点,然后前序遍历左子树,再前序遍历右子树
中序遍历(左 根 右)
中序遍历根结点的左子树,然后访问根结点,最后遍历右子树
后序遍历(左 右 根)
从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点
层级遍历(从上到下 从左到右)
从根结点从上往下从左往右依次遍历
思路
非递归:
前序遍历:从根节点开始,首先将根节点压入栈中,栈不为空进行出栈并打印结点的value数值,然后将该结点的不为空的右结点和左结点依次进行入栈操作重复直到栈为空。
后序遍历:从根节点开始,首先将根节点压入栈中,栈不为空进行出栈并入栈到另一个栈中,然后将该结点的不为空的左结点和右结点依次进行入栈操作重复直到栈为空。然后遍历另一个栈进行出栈并打印结点的值。
中序遍历:从根节点开始将该结点以及它的左边界依次进行入栈,当该结点为null时,然后进行出栈操作,打印出栈结点的value数值,并入栈弹出结点的右结点,然后重复上述步骤,继续入栈该结点的左边界直到为空。。。。
层次遍历:从根节点放入队列,队列不为空的时候进行出队列并打印该结点的value数值,然后依次将该结点的左结点和右结点进行放入队列,一直重复直到队列为空。
代码
Node结点
public class Node<V> {V value;public Node(V value) {this.value = value;}public Node left;public Node right;
}
遍历代码
public class Tree {//递归先序遍历public static void preOrder1(Node head){if(head!=null){System.out.print(head.value+" ");preOrder1(head.left);preOrder1(head.right);}}//先序遍历public static void preOrder(Node head){if(head!=null){Stack<Node> stack=new Stack<>();stack.add(head);//压到栈尾while (!stack.empty()){head=stack.pop();System.out.print(head.value+" ");if(head.right!=null)stack.push(head.right);if(head.left!=null)stack.push(head.left);}}System.out.println();}//后序遍历public static void postOrder(Node head){if(head!=null){Stack<Node> stack1=new Stack<>();Stack<Node> stack2=new Stack<>();stack1.push(head);while (!stack1.empty()){head = stack1.pop();stack2.push(head);if(head.left!=null)stack1.push(head.left);if(head.right!=null)stack1.push(head.right);}while (!stack2.empty()){Node pop = stack2.pop();System.out.print(pop.value+" ");}System.out.println();}}//中序遍历public static void inOrder(Node head){Stack<Node> stack=new Stack<>();while (!stack.empty()||head!=null){if(head!=null){stack.push(head);head=head.left;}else {head=stack.pop();System.out.print(head.value+" ");head=head.right;}}System.out.println();}//层次遍历public static void widthOrder(Node head){if(head!=null){Queue<Node> queue=new LinkedList<>();queue.add(head);while (!queue.isEmpty()){Node poll = queue.poll();System.out.print(poll.value+" ");if(poll.left!=null)queue.add(poll.left);if(poll.right!=null){queue.add(poll.right);}}}System.out.println();}}相关文章:

Java 二叉树的遍历
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有的结点,使得每个结点被访问依次且仅被访问一次。前序遍历(根 左 右)先访问根结点,然后前序遍历左子树…...

实习日记-C#
数据类型 字符串常量 string a "hello, world"; // hello, world string b "hello, world"; // hello, world string c "hello \t world"; // hello world string d "hello \t wor…...
Tech Lead如何引导团队成员解决问题?
作为一个开发团队的Tech Lead,当团队成员向你寻求帮助时,你有没有说过下面这些话? 你别管了,我来解决这个问题你只要。。。就行了你先做其他的吧,我研究一下,然后告诉你怎么做 当我们说这些话时ÿ…...
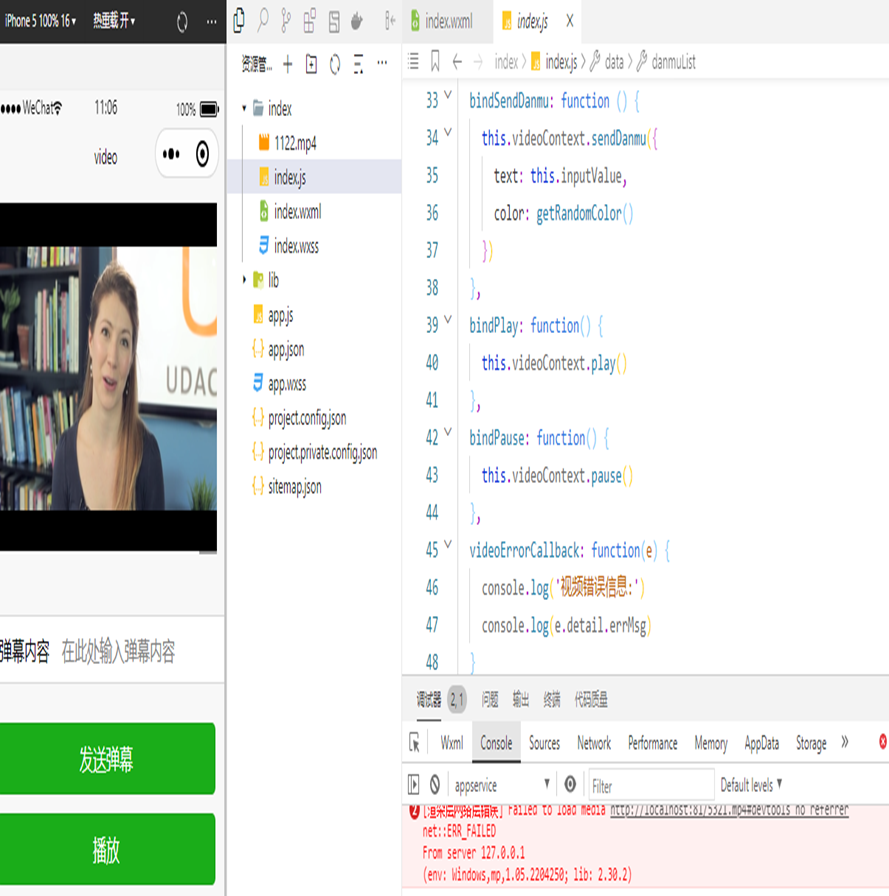
07--组件
一、小程序组件分类微信团队为开发者提供了一系列基础组件,开发者可以通过组合这些基础组件进行快速开发。小程序中的组件也是非常丰富的,开发者可以基于组件快速搭建出漂亮的页面结构。小程序中的组件其实相当于网页中的HTML标签,只不过标签…...

怎么做好一个完整的项目复盘
复盘,是运营必不可少的能力,小到一次买菜的经历,大到百亿千亿的投资项目,都可以通过复盘来总结规律、提升水平。简单说来,复盘可以达到的效果有两条:优化弱项,强化强项明确自己的价值࿰…...
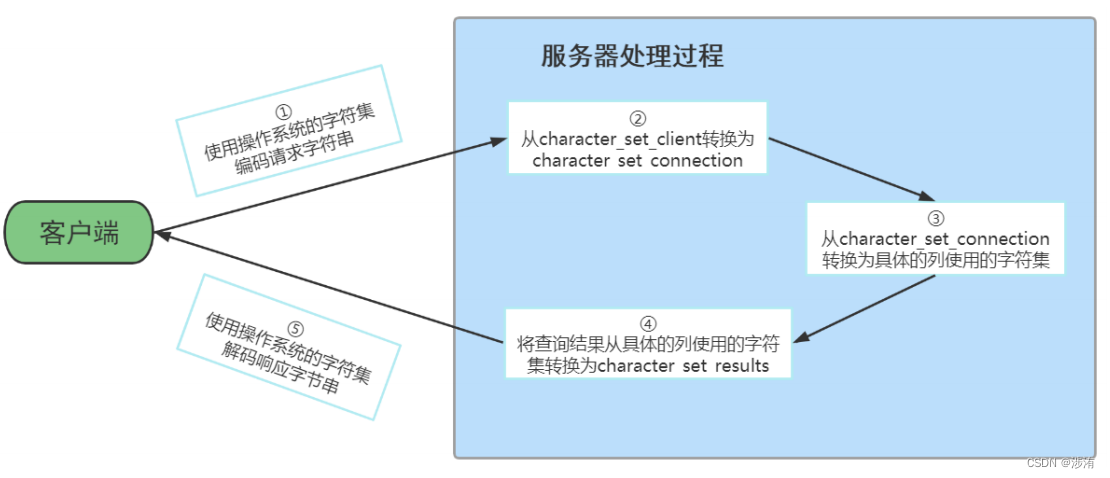
浅谈一下mysql8.0与5.7的字符集
修改字符集 修改步骤 在MySQL8.0版本之前,默认字符集为1atin1,utf8字符集指向的是utf8mb3。网站开发人员在数据库设计的时候往往会将编码修改为ut8字符集。如果遗忘修改默认的编码,就会出现乱码的问题。从MySQL8.0开始,数据库的默认编码将改…...
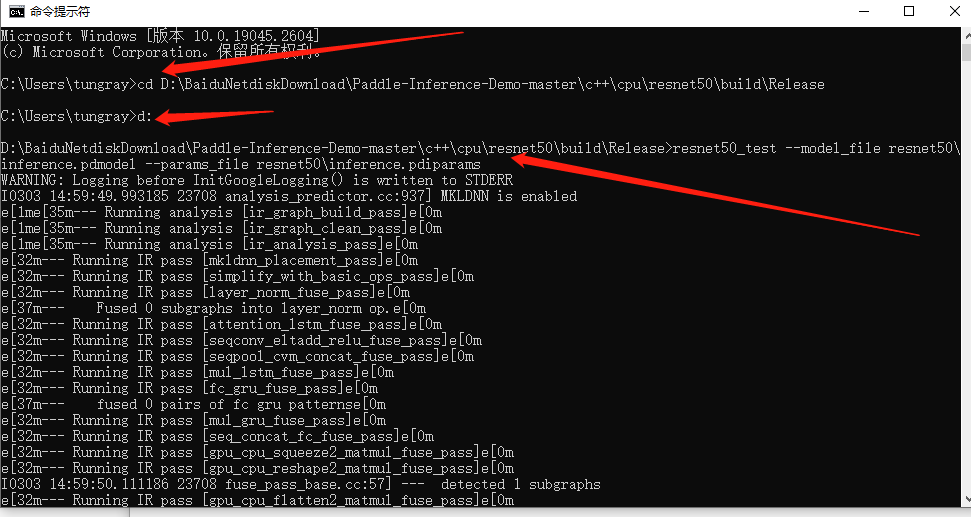
paddle推理部署(cpu)
我没按照官方文档去做,吐槽一下,官方文档有点混乱。。一、概述总结起来,就是用c示例代码,用一个模型做推理。二、示例代码下载https://www.paddlepaddle.org.cn/paddle/paddleinferencehttps://github.com/PaddlePaddle/Paddle-In…...

想开发IM集群?先搞懂什么是RPC!
即时通讯网官方技术群和社区里,经常有开发者在纠结怎么开发IM集群,虽然真正的使用人数,可能用个人电脑单机都能支撑。你也许会说,明明不需要用到IM集群,干吗要自找麻烦?答曰:“老板说这个得有&a…...
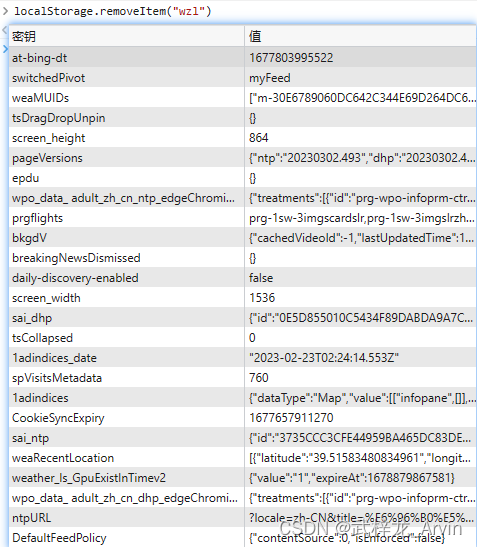
案例13-前端对localStorage的使用分析
一:背景介绍 前端在调用后端接口获取某一个人的评论次数、获赞次数、回复次数。调用之后判断后端返回过来的值。如果返回回来的值是0的话,从缓存中获取对应的值,如果从缓存中获取的评论次数为空那么其他两个的次数也为0。 二:思路…...

CNNIC第51次中国互联网络发展状况统计报告用户规模变化发布、解读与白杨SEO看法
一、第51次《中国互联网络发展状况统计报告》发布 3月2日,中国互联网络信息中心(简称CNNIC)在京发布第51次《中国互联网络发展状况统计报告》。《报告》显示,截至2022年12月,我国网民规模达10.67亿,较2021…...

【数据结构】单链表的实现
本篇主要总结单链表是如何实现的,数据结构是如何管理数据的,详细的介绍每一步是如何实现以及各种注意事项。🚀1.单链表的实现🚀🍭1.1单链表的尾插🍭1.2单链表的头插🍭1.3单链表的打印dz…...

从0到1做产品!产品设计的6个步骤
相信不少产品经理在刚入行时,都遇到过这样的情况: 接到需求后不知所措,然后下意识地照着竞品开始盲目地画原型。 其实,这样的设计过程不仅缺乏逻辑性,在后续阶段也很容易出现各种问题。 在此,跟大家分享一下…...

ESP32遥控器软硬件设计
一. 前言 做智能车 或者 四轴飞控怎么能少得了遥控器呢!在这里给大家分享一个简单的基于ESP32遥控器的设计,包括软硬件以及3D外壳。 二. 硬件设计 1. 功能介绍 遥控器嘛,通信方式是最重要的,本设计支持 WIFI、蓝牙 和 2.4G&…...
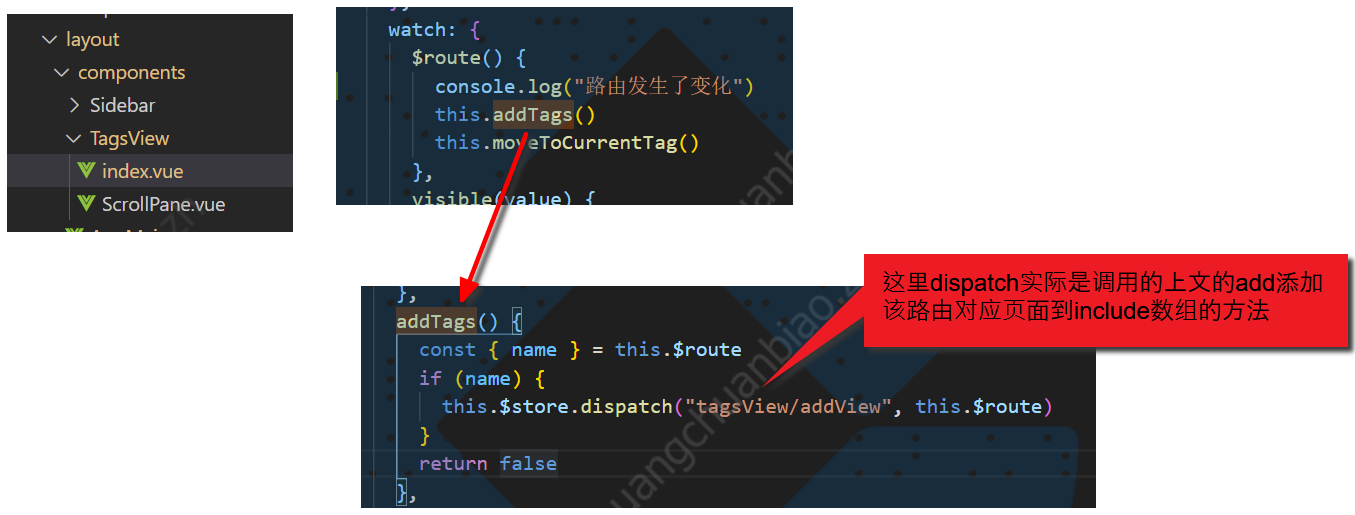
vue-template-admin的keep-alive缓存与移除缓存
一,场景 A页面是表单页面,填写后需要跳转B页面。如果B页面不操作返回的话,应该能还原A页面的内容,而如果B页面点击提交,再回到A页面的时候,应该清除缓存。 二,实现方法 A页面要缓存数据&…...

【人工智能 AI】机器学习快速入门教程(Google)
目录 机器学习术语 标签 特性 示例 模型 回归与分类 深入了解机器学习:线性回归 深入了解机器学习:训练和损失 平方损失函数:一种常用的损失函数 机器学习术语 预计用时:8 分钟 什么是(监督式ÿ…...
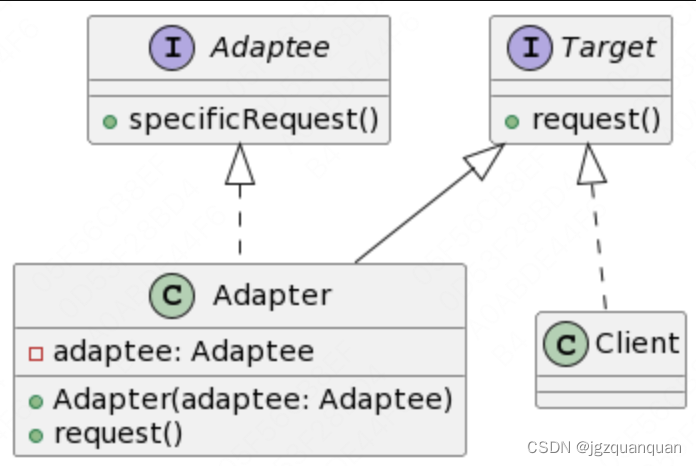
适配器模式
概览 适配器模式是一种结构型设计模式,用于将一个类的接口转换为客户端所期望的另一种接口。通常情况下,这种转换是由一个适配器类完成的,适配器类包装了原始类,并实现了客户端所期望的接口。这种模式非常适用于在不修改现有代码…...
00后跨专业学软件测试,斩获8.5K高薪逆袭职场
我想说的第一句:既然有梦想,就应该去拼搏还记得,我大学毕业前,就已经暗下决心到xxx培训机构接受培训。那个时候,没有任何海同公司的人主动找我或者联系过我,我是自己在网上发现了xxxx培训机构的!…...
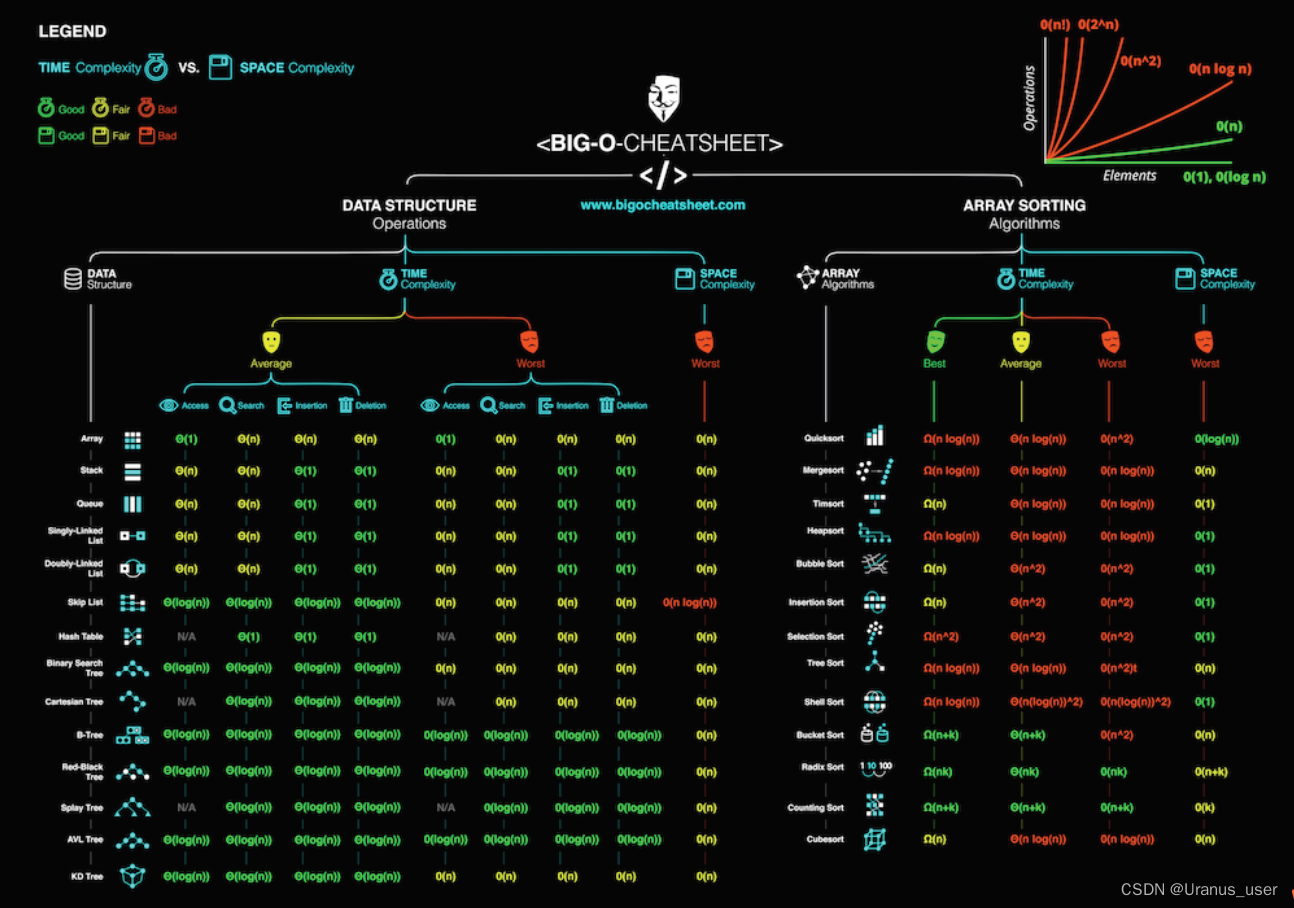
数据结构和算法学习
文章目录精通一个领域切题四件套算法算法的五个条件流程图数据结构数据与信息数据信息数据结构和算法数据结构算法时间复杂度空间复杂度数组 Array优点缺点数组和链表的区别时间复杂度链表 Linked List优点缺点时间复杂度单向链表双向链表循环链表双向循环链表堆栈 Stack队列 Q…...

剑指 Offer II 012. 左右两边子数组的和相等
题目链接 剑指 Offer II 012. 左右两边子数组的和相等 easy 题目描述 给你一个整数数组 nums,请计算数组的 中心下标 。 数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。 如果中心下标位于数组最左端,那…...

Java货物摆放
题目描述 小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 � n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。 小蓝希望所…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
