【上分日记】第369场周赛(分类讨论 + 数学 + 前缀和)
文章目录
- 前言
- 正文
- 1.3000. 对角线最长的矩形的面积
- 2.3001. 捕获黑皇后需要的最少移动次数
- 3.3002. 移除后集合的最多元素数
- 3.3003. 执行操作后的最大分割数量
- 总结
- 尾序
前言
终于考完试了,考了四天,也耽搁了四天,这就赶紧来补这场周赛的题了,这场周赛博主只写了两道题,第一题和第三题 ( hhh, 菜鸡勿喷),这场周赛挺有难度,也挺有意思的,第二题是个国际象棋,我都没下过,分类讨论也是有点困难。做出来的也有思路不顺的,下面我们把这四道题从头到尾总结一下。
正文
1.3000. 对角线最长的矩形的面积
-
题目链接:对角线最长的矩形的面积
-
题目思路:
- 先求出对角线的平方,等同于计算对角线。
- 不断更新最长的对角线的平方与其面积,如果相等,则取面积最大的。
- 实现代码:
class Solution {
public:int areaOfMaxDiagonal(vector<vector<int>>& dimensions) {int diag = 0;int area = 0;for(auto v : dimensions){int val = v[0]*v[0] + v[1]*v[1];int s = v[0]*v[1];if(val > diag ||(val == diag && s > area)){diag = val;area = s;}}return area; }
};
2.3001. 捕获黑皇后需要的最少移动次数
-
题目链接:捕获黑皇后需要的最少移动次数
-
数学知识:
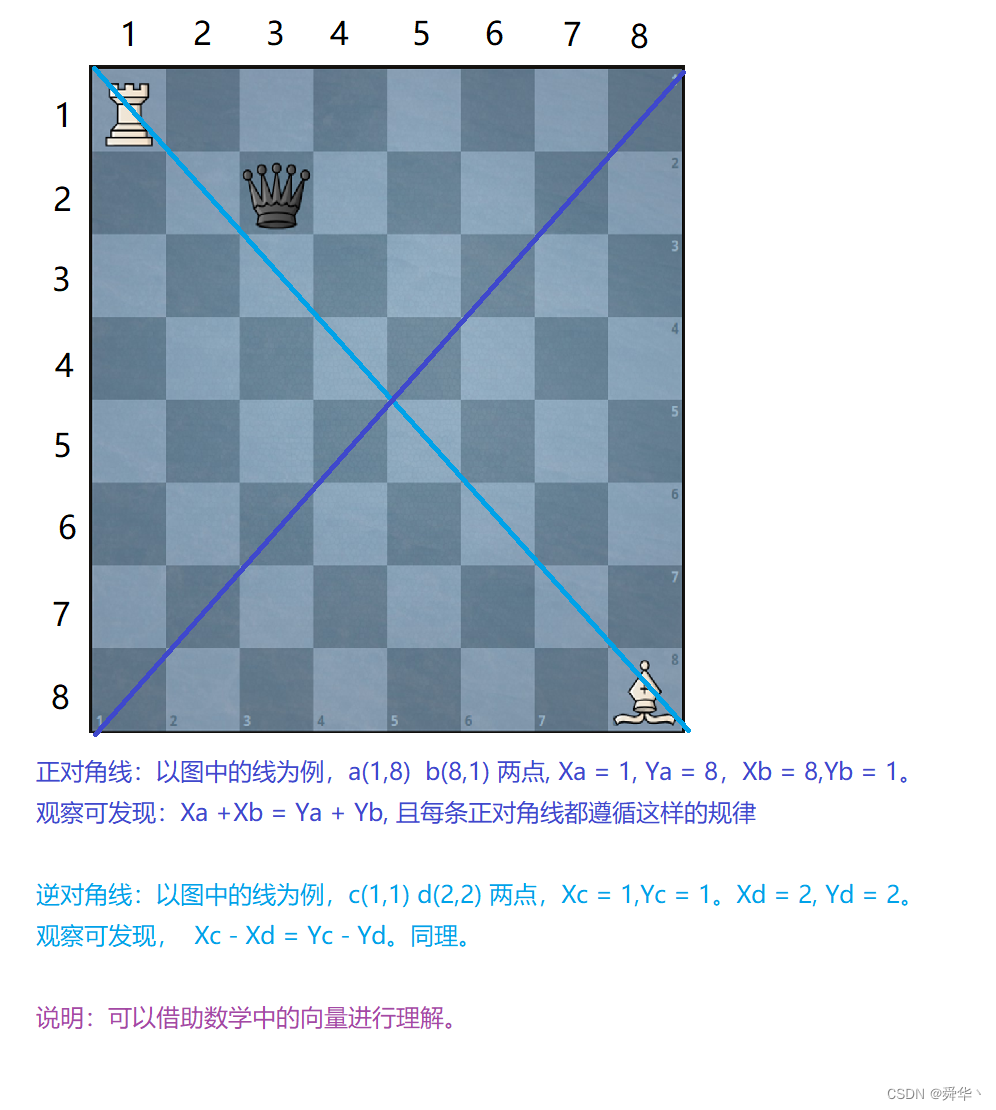
- 说明:这个不知道,写这道题难度会上升不少。
- 我们先来进行分类讨论。
- 车
1.1 车一步到达:
- 说明: 闪击战术
2.2 车两步到达,只要不是一步,必然是两步到达。
- 象
2.1 象一步到达。
2.2 象两步,或者如果象与皇后所在格子的颜色不同的话,只移动象是到不了皇后的。
-
总结,因为有车兜底,所以最多两步,一步的话分情况讨论即可。
-
实现代码:
class Solution {
public:int minMovesToCaptureTheQueen(int a, int b, int c, int d, int e, int f) {//先分析车的auto is_in = [&](int left,int right,int x){int _left = min(left,right);int _right = max(left,right);return !(x >_left && x <_right);};auto check_car = [&](){if(( e == a && (c != a || is_in(f,b,d)) )//行相等|| ( f == b && (d != b || is_in(e,a,c)) ) //列相等) return 1;return 2;};auto check_ele = [&](){if((c + f == e + d &&(c + b != a + d || is_in(c,e,a)) //正对角线|| (c - f == e - d && (c -b != a - d || is_in(c,e,a))))//逆对角线)return 1;return 2;};return min(check_car(),check_ele());}
};
3.3002. 移除后集合的最多元素数
-
题目链接:移除后集合的最多元素数
-
题目思路:
- 在实际过程中,博主是模拟进行求解的,即先将集合分别去重,然后去掉集合元素较多的两个集合的共同元素,然后取两个长度与原本的长度的二分之一进行比较,取较小的。最后返回两者之和即可。
class Solution {
public:int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {//第一步:对自身去重unordered_set<int> gather1(nums1.begin(),nums1.end()),\gather2(nums2.begin(),nums2.end());int ans1 = gather1.size(),ans2 = gather2.size()\,sz1 = nums1.size() / 2,sz2 = nums2.size() / 2;//第二步:去掉两个集合中重复的,且去的是较长的那一个。for(auto e : gather1){if(gather2.count(e)){if(ans2 > ans1)ans2--;elseans1--;}}//第三步:取min求预期值。return min(ans1,sz1) + min(ans2,sz2);}
};
- 看了灵神的题解,直接进行讨论也可以,是利用重复元素出现的个数,要想达到最长,关键是先去重复的,然后再去不重复的。
- 实现代码:
class Solution {
public:int maximumSetSize(vector<int>& nums1, vector<int>& nums2) {unordered_set<int> gather1(nums1.begin(),nums1.end())\,gather2(nums2.begin(),nums2.end());//第一步对自身去重//第二步求出并集的个数int key = 0;for(auto e : gather1){if(gather2.count(e)) key++;}//第三步分类讨论//优先取消并集元素,也就是并集元素有两条命。int ans1 = gather1.size(),sz1 = nums1.size() / 2;int ans2 = gather2.size(),sz2 = nums2.size() / 2;auto ajust = [&](int ans,int sz){if(ans > sz){int need = ans - sz;if(key > need){key -= need; ans -= need,need = 0;}else{need -= key; ans -= key; key = 0;}ans -= need;}return ans;};return ajust(ans1,sz1) + ajust(ans2,sz2) - key;}
};
3.3003. 执行操作后的最大分割数量
- 题目链接:执行操作后的最大分割数量
- 题目大致意思:
- 我们只能执行一次,即 将s[i] 修改为 26个字母中的一个。
- 且 i 只能在前缀s 中。
- 求最大分割数量。
- 前置知识:
- s从前往后分割,与s从后往前分割,段数相同。
- 题目思路:
class Solution {
public:int maxPartitionsAfterOperations(string s, int k) {/*如果总的字符串小于k,即使修改一个字符,也只能等于k,还是只能划分一段。*/int mask = 0,kinds = 0;for(char ch : s){int key = 1 << (ch - 'a');if(!(mask & key)){++kinds;mask |= key;}}if(kinds < k || k == 26) return 1;/*如果需要的字符串种类等于26,那么只能切到最后,且无法再通过修改字符,增加段数。*/int sz = s.size(),seg = 1;kinds = 0,mask = 0;vector<pair<int,int>> suf(sz + 1);/*mask: 用于位运算记录字符种类的掩码。segment:段,记录前缀或者后缀的分成的段数,最少划分一段。suffix: 后缀,即suf,记录能划分的段数与最近一段的mask。*/auto update = [&](int i){int key = 1 << (s[i] - 'a');if(!(mask & key)){//记录字符串的种类。mask |= key;if(++kinds > k){/*此时key也在mask里面。*/seg++;mask = key;kinds = 1;}}return;};for(int i = sz - 1; i >= 0; i--){update(i);suf[i] = {seg,mask};}int ans = seg; //最小的分割段数,且后缀与前缀分的结果是相同的。seg = 1,mask = 0,kinds = 0;for(int i = 0; i < sz; i++){/*以i为分界线进行讨论,[L,i),(i + 1, R]*/auto [suf_seg,suf_mask] = suf[i+1];//[L,R]是多于的一段,这一段,也可能可以划分。int res = suf_seg + seg;//默认为其它情况,其它情况是在此基础上进行加一或者减一。int unionmask = suf_mask | mask;if(__builtin_popcount(unionmask) < k){//只能合并,且会少一段res--;}else if(__builtin_popcount(suf_mask) == k && kinds == k&&__builtin_popcount(unionmask) < 26){//会多出一个s[i]字符,因此会增加一段res++;}//更新三种情况的最大值。ans = max(ans,res); update(i);}return ans;}
};
- 注 :本题的思路主要参考灵神的题解。
总结
综合来说,这几道题都侧重于分类讨论,其中还牵扯到一些数学的知识,以及有趣的国际象棋,最后一题则需要借助前后缀 + 数学知识 + 分类讨论进行判断。
尾序
我是舜华,期待与你的下一次相遇!
相关文章:
【上分日记】第369场周赛(分类讨论 + 数学 + 前缀和)
文章目录 前言正文1.3000. 对角线最长的矩形的面积2.3001. 捕获黑皇后需要的最少移动次数3.3002. 移除后集合的最多元素数3.3003. 执行操作后的最大分割数量 总结尾序 前言 终于考完试了,考了四天,也耽搁了四天,这就赶紧来补这场周赛的题了&a…...
: The CMAKE_CXX_COMPILER:)
CMake Error at CMakeLists.txt:14 (project): The CMAKE_CXX_COMPILER:
报错 CMake Error at CMakeLists.txt:14 (project):The CMAKE_CXX_COMPILER:arm-none-eabi-g 解决办法1 Arm GNU Toolchain Downloads – Arm Developer x86_64 linux上: x86_64 Linux hosted cross toolchains AArch32 bare-metal target (arm-none-eabi)arm-g…...

Sqoop与其他数据采集工具的比较分析
比较Sqoop与其他数据采集工具是一个重要的话题,因为不同的工具在不同的情况下可能更适合。在本博客文章中,将深入比较Sqoop与其他数据采集工具,提供详细的示例代码和全面的内容,以帮助大家更好地了解它们之间的差异和优劣势。 Sq…...

Pandas实战100例 | 案例 31: 转换为分类数据
案例 31: 转换为分类数据 知识点讲解 在处理包含文本数据的 DataFrame 时,将文本列转换为分类数据类型通常是一个好主意。这可以提高性能并节省内存。Pandas 允许将列转换为 category 类型。 分类数据类型: category 类型适用于那些只包含有限数量不同值的列&…...

椋鸟C语言笔记#33:文件的顺序读写
萌新的学习笔记,写错了恳请斧正。 目录 光标(文件位置指示器) 文件的顺序读写 fgetc 使用实例 fputc 使用实例 fgets fputs 使用实例 fscanf fprintf fread fwrite 使用实例 光标(文件位置指示器) 我们…...

Transformer - Attention is all you need 论文阅读
虽然是跑路来NLP,但是还是立flag说要做个project,结果kaggle上的入门project给的例子用的是BERT,还提到这一方法属于transformer,所以大概率读完这一篇之后,会再看BERT的论文这个样子。 在李宏毅的NLP课程中多次提到了…...

安装配置Flink
安装配置Flink 1.上传安装包到Linux 2.解压到指定路径 tar -zxf ./flink-1.14.0-bin-scala_2.12.tgz /usr/local/src/3.修改环境变量 vi ~/.bashrc#往最后加入 export FLINK_HOME /usr/local/src/flink-1.14.0/ export PATH$PATH:$FLINK_HOME/bin#激活环境变量 source ~/.…...
解决Spss没有创建虚拟变量的选项的问题
这个是今天用spss想创建虚拟变量然后发现我的spss没有。 然后能怎么办我就百度呗, 说是在扩展里连接扩展中心 天哪,谁能连上,我连不上 于是就找到了从github上下载到本地,然后安装到spss中 目录 解决方法 点击code 再点击D…...

wxWidgets实战:使用mpWindow绘制阻抗曲线
选择模型时,需要查看model的谐振频率,因此需要根据s2p文件绘制一张阻抗曲线。 如下图所示: mpWindow 左侧使用mpWindow,右侧使用什么? wxFreeChart https://forums.wxwidgets.org/viewtopic.php?t44928 https://…...
冻结和解冻神经网络模型的参数)
深度学习15—(迁移学习)冻结和解冻神经网络模型的参数
冻结与解冻代码: def freeze_net(net):if not net:returnfor p in net.parameters():p.requires_grad Falsedef unfreeze_net(net):if not net:returnfor p in net.parameters():p.requires_grad True 这段代码定义了两个函数:freeze_net 和 unfree…...

强化学习应用(八):基于Q-learning的无人机物流路径规划研究(提供Python代码)
一、Q-learning简介 Q-learning是一种强化学习算法,用于解决基于马尔可夫决策过程(MDP)的问题。它通过学习一个价值函数来指导智能体在环境中做出决策,以最大化累积奖励。 Q-learning算法的核心思想是通过不断更新一个称为Q值的…...

常见面试题之HTML
行内元素有哪些?块级元素有哪些? 空(void)元素有那些? HTML 中的行内元素(inline elements)通常用于在一行内显示,不会独占一行的空间。常见的行内元素有: <span>:用于对文本…...

数据结构与算法教程,数据结构C语言版教程!(第三部分、栈(Stack)和队列(Queue)详解)六
第三部分、栈(Stack)和队列(Queue)详解 栈和队列,严格意义上来说,也属于线性表,因为它们也都用于存储逻辑关系为 "一对一" 的数据,但由于它们比较特殊,因此将其单独作为一章,做重点讲解。 使用栈…...

使用Docker部署PDF多功能工具Stirling-PDF
1.服务器上安装docker 安装比较简单,这种安装的Docker不是最新版本,不过对于学习够用了,依次执行下面命令进行安装。 sudo apt install docker.io sudo systemctl start docker sudo systemctl enable docker 查看是否安装成功 $ docker …...

linux安装系统遇到的问题
这两天打算攻克下来网络编程,发现这也确实是很重要的一个东西,但我就奇了怪了,老师就压根没提,反正留在我印象的就一个tcp/ip七层网络。也说正好,把linux命令也熟悉熟悉,拿着我大一课本快速过过 连接cento…...

groovy XmlParser 递归遍历 xml 文件,修改并保存
使用 groovy.util.XmlParser 解析 xml 文件,对文件进行修改(新增标签),然后保存。 是不是 XmlParser 没有提供方法遍历每个节点,难道要自己写? 什么是递归? 不用说,想必都懂得~ …...
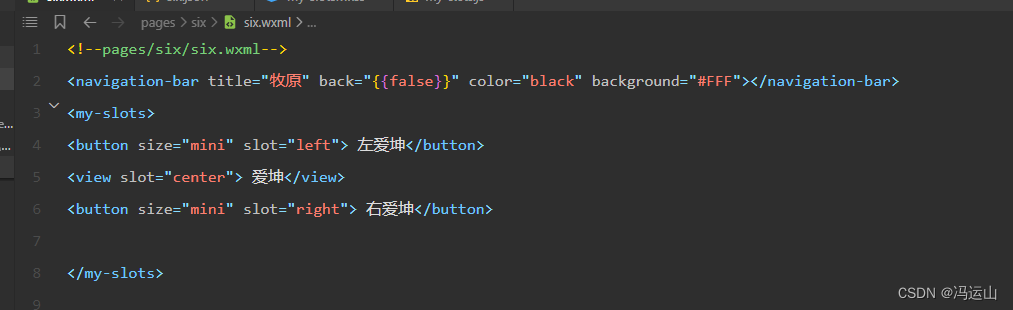
小程序基础学习(多插槽)
先创建插槽 定义多插槽的每一个插槽的属性 在js文件中启用多插槽 在页面使用多插槽 组件代码 <!--components/my-slots/my-slots.wxml--><view class"container"><view class"left"> <slot name"left" ></slot>&…...
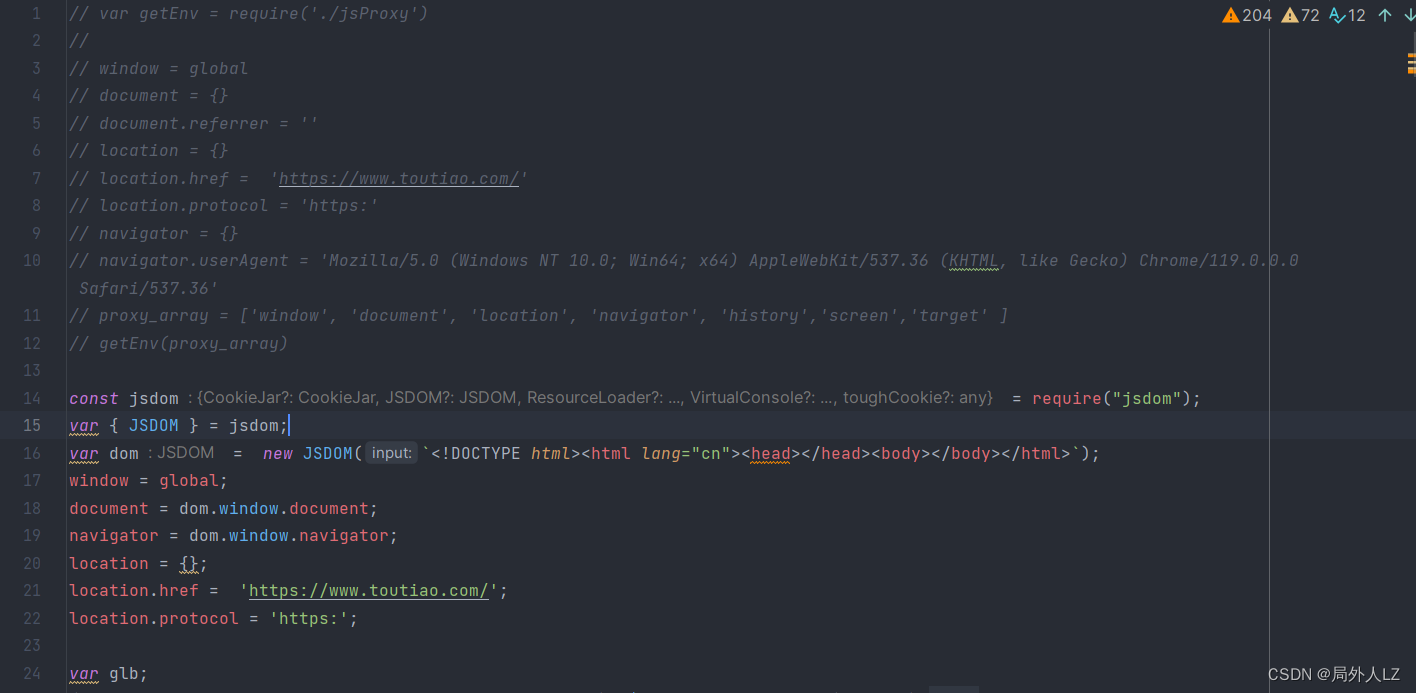
爬虫补环境jsdom、proxy、Selenium案例:某条
声明: 该文章为学习使用,严禁用于商业用途和非法用途,违者后果自负,由此产生的一切后果均与作者无关 一、简介 爬虫逆向补环境的目的是为了模拟正常用户的行为,使爬虫看起来更像是一个真实的用户在浏览网站。这样可以…...

电子学会C/C++编程等级考试2021年09月(四级)真题解析
C/C++编程(1~8级)全部真题・点这里 第1题:最佳路径 如下所示的由正整数数字构成的三角形: 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,和最大的路径称为最佳路径。你的任务就是求出最佳路径…...

DevExpress历史安装文件包集合
Components - DevExpress.NET组件安装包此安装程序包括所有 .NET Framework、.NET Core 3 和 .NET 5、ASP.NET Core 和 HTML/JavaScript 组件和库(Web和桌面应用程序开发只需要安装此文件即可)。 注意:自DevExpress21.1版本之后,该…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...