力扣-213打家劫舍II(dp)
力扣-213打家劫舍II
1、题目
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
2、分析
- 题目。这题与198打家劫舍唯一不同的就是首尾是相连的,所以遍历的时候要首不要尾,或者要尾不要首,就这两种情况。
- 看到这个题目首先想到的是不能相邻,那么如果要偷其中i的一家,那么我们就需要考虑前面一家i-1就不能偷,i-2的一家就能够偷了,所以,我们大概能够知道这是一道动态规划问题。
- 根据上面的分析,dp[i]就是我们偷当前i家的时候,最大金额数。那么我们可得地推公式为:dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])。
初始化。 - 遍历,两种情况,多个函数进行区间调用。
3、代码及注释
class Solution {public int rob(int[] nums) {// 1.第一种就是要最后一个房屋// 2.第二种就是不要最后一个房屋if (nums.length == 0) return 0;if (nums.length == 1) return nums[0];if (nums.length == 2) return Math.max(nums[0], nums[1]);return Math.max(robRange(nums, 0, nums.length - 1), robRange(nums, 1, nums.length));}public int robRange(int[] nums, int start, int end){int[] dp = new int[end];dp[start] = nums[start];dp[start + 1] = Math.max(nums[start + 1], dp[start]);for (int i = start + 2; i < end; i++){dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[end - 1];}
}
4、练习
力扣题目链接:213. 打家劫舍 II
相关文章:
)
力扣-213打家劫舍II(dp)
力扣-213打家劫舍II 1、题目 213. 打家劫舍 II 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通…...
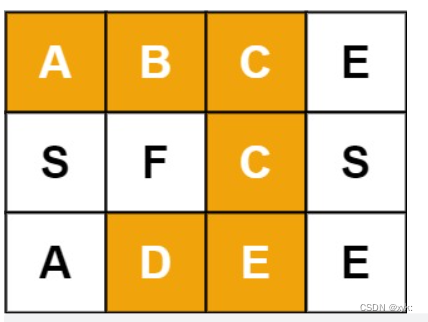
关于【网格结构】岛屿类问题的通用解法DFS(深度遍历)遍历框架+回溯+剪枝总结
最近在刷力扣时遇见的问题,自己总结加上看了力扣大佬的知识总结写下本篇文章,我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题…...

【LeetCode】982. 按位与为零的三元组
982. 按位与为零的三元组 题目描述 给你一个整数数组 nums ,返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组,并满足下述全部条件: 0 < i < nums.length0 < j < nums.length0 < k < num…...

Linux内核源码进程原理分析
Linux内核源码进程原理分析一、Linux 内核架构图二、进程基础知识三、Linux 进程四要素四、task_struct 数据结构主要成员五、创建新进程分析六、剖析进程状态迁移七、写时复制技术一、Linux 内核架构图 二、进程基础知识 Linux 内核把进程称为任务(task),进程的虚…...

电子技术——CMOS反相器
电子技术——CMOS反相器 在本节,我们深入学习CMOS反相器。 电路原理 下图是我们要研究的CMOS反相器的原理图: 下图展示了当输入 vIVDDv_I V_{DD}vIVDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线: 我们把 QNQ_NQN 当做是驱动源&#x…...
)
gazebo仿真轨迹规划+跟踪(不在move_base框架下)
以Tianbot为例子,开源代码如下: https://github.com/tianbot/tianbot_mini GitHub - tianbot/abc_swarm: Ant Bee Cooperative Swarm, indicating air-ground cooperation. This repository is for Tianbot Mini and RoboMaster TT swarm kit. 1.在…...

C. Good Subarrays(前缀和)
C. Good Subarrays一、问题二、分析三、代码一、问题 二、分析 这道题目的意思就是给我们一个数组,然后我们从数组中选取一个连续的区间,这个区间满足条件:区间内的元素和等于区间的长度。 对于区间和问题我们先想到的是前缀和的算法。 那…...
关于Facebook Messenger CRM,这里有你想要知道的一切
关于Facebook Messenger CRM,这里有你想要知道的一切!想把Facebook Messenger与你的CRM整合起来吗?这篇博文是为你准备的! 我们将介绍有关获得Facebook Messenger CRM整合的一切信息。然后,我们将解释为什么你需要像SaleSmartly&a…...
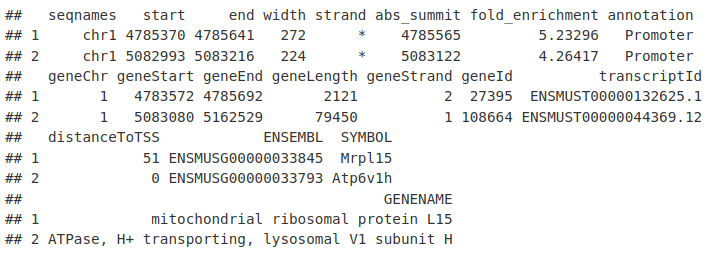
ChIP-seq 分析:数据与Peak 基因注释(10)
动动发财的小手,点个赞吧! 1. 数据 今天,我们将继续回顾我们在上一次中研究的 Myc ChIPseq。这包括用于 MEL 和 Ch12 细胞系的 Myc ChIPseq。 可在此处[1]找到 MEL 细胞系中 Myc ChIPseq 的信息和文件可在此处[2]找到 Ch12 细胞系中 Myc ChIP…...
)
《C++ Primer Plus》第18章:探讨 C++ 新标准(8)
使用大括号括起的初始化列表语法重写下述代码。重写后的代码不应使用数组 ar: class Z200 { private:int j;char ch;double z; public:Z200(int jv, char chv, zv) : j(jv), ch(chv), z(zv) {} ... };double x 8.8; std::string s "What a bracing effect!&q…...
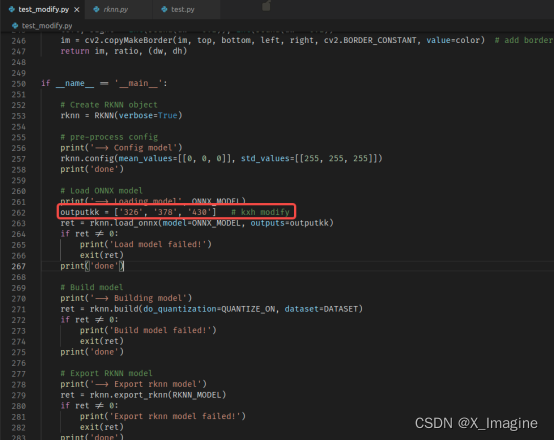
YOLO-V5 系列算法和代码解析(八)—— 模型移植
文章目录工程目标芯片参数查阅官方文档基本流程Python 版工具链安装RKNPU2的编译以及使用方法移植自己训练的模型工程目标 将自己训练的目标检测模型【YOLO-V5s】移植到瑞芯微【3566】芯片平台,使用NPU推理,最终得到正确的结果。整个过程涉及模型量化、…...

js实现复制拷贝的兼容方法
1. 定义复制拷贝的方法 在某个工具类方法中定义该方法,兼容不同浏览器处理 /*** description 拷贝的类方法*/ class CopyClass {// constructor() {}setRange(input) {return new Promise((resolve, reject) > {try {// 创建range对象const range document.c…...
学习 Python 之 Pygame 开发魂斗罗(八)
学习 Python 之 Pygame 开发魂斗罗(八)继续编写魂斗罗1. 创建敌人类2. 增加敌人移动和显示函数3. 敌人开火4. 修改主函数5. 产生敌人6. 使敌人移动继续编写魂斗罗 在上次的博客学习 Python 之 Pygame 开发魂斗罗(七)中࿰…...
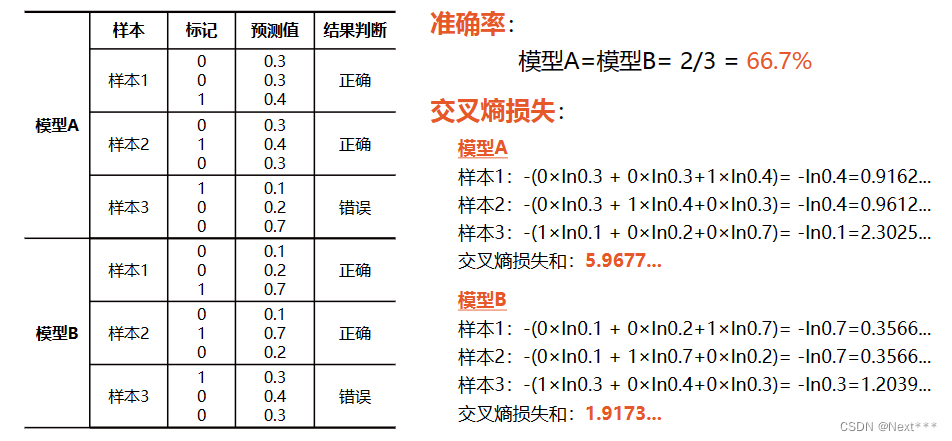
Lesson11---分类问题
11.1 逻辑回归 11.1.1 广义线性回归 课程回顾 线性回归:将自变量和因变量之间的关系,用线性模型来表示;根据已知的样本数据,对未来的、或者未知的数据进行估计 11.1.2 逻辑回归 11.1.2.1 分类问题 分类问题:垃圾…...

Python基础学习12——异常
在Python中,会使用“异常”这个十分特殊的对象来管理程序执行期间发生的错误,即报错。本文将介绍一下python基础的处理异常的方法以及一些基本的异常类型。 异常处理方法 try-except代码块 当我们编写程序时,我们可以编写一个try-except代…...

[日常练习]练习17:链表头插法、尾插法练习
[日常练习]练习17:链表头插法、尾插法练习练习17描述输入输出输入示例1输出示例1输入示例2输出示例2代码演示:总结练习17 【日常练习】 链表头插法、尾插法练习 描述 输入3 4 5 6 7 9999一串整数,9999代表结束,通过头插法新建链…...
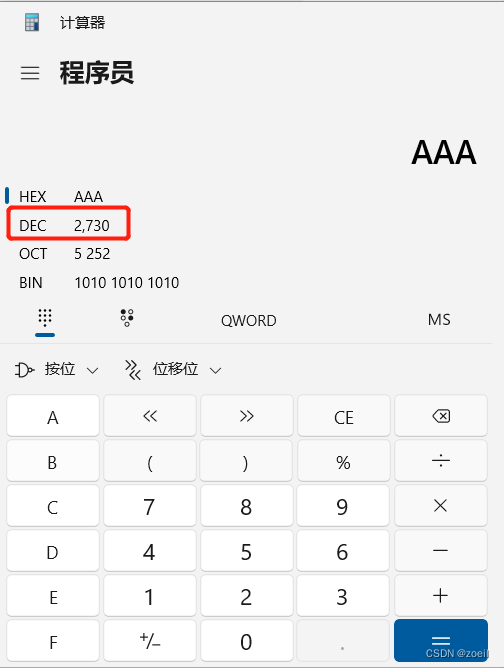
第十四届蓝桥杯模拟赛(第三期)试题与题解 C++
目录 一、填空题 (一)最小的十六进制(答案:2730) (二)Excel的列(答案:BYT) (三)相等日期(答案:70910) (四)多少种取法(答案:189)…...

关于 “宏“
起源 宏 Macro"这个词源于希腊语 “makros”,意为“大的,长的” 延伸使用 随后用于计算机领域是,在汇编语言时用于描述一大堆的汇编指令。 只要用宏指令,就是直接用的一大堆的汇编指令(有点函数的味道…...

1.2 CSS标签选择器,类选择器
CSS选择器: 根据不同的需求选出不同的标签,进行美化装饰 1. 标签选择器 标签选择器(元素选择器):用 HTML标签名作为选择器,按标签名称进行分类,为页面某一类标签指定统一的CSS样式 作用: 可以把某一类标签全部选中&…...

【Linux】进程等待 | 详解 wait/waitpid 的 status 参数
🤣 爆笑教程 👉 《看表情包学Linux》👈 猛戳订阅 🔥 💭 写在前面:在上一章中我们讲解了进程创建与进程终止,本章我们开始讲解进程等待。进程等待这部分知识相较于前面还是较为复杂的࿰…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
