【华为OD机试2023】静态扫描 C++ Java Python
【华为OD机试2023】静态扫描 C++ Java Python
前言
如果您在准备华为的面试，期间有想了解的可以私信我，我会尽可能帮您解答，也可以给您一些建议！
本文解法非最优解（即非性能最优），不能保证通过率。
Tips1：机试为ACM 模式
你的代码需要处理输入输出，input/cin接收输入、print/cout 格式化输出
Tips2：机试按通过率算分
复杂题目可以考虑暴力破解，再逐步优化，不是运行超时就无法得分，比如一个分数为200的题目，当前通过率为50%，那么最终分数就是200*50%=100分
题目
题目描述
静态扫描可以快速识别源代码的缺陷，静态扫描的结果以扫描报告作为输出：
1、文件扫描的成本和文件大小相关，如果文件大小为N，则扫描成本为N个金币
2、扫描报告的缓存成本和文件大小无关，每缓存一个报告需要M个金币
3、扫描报告缓存后，后继再碰到该文件则不需要扫描成本，直接获取缓存结果
给出源代码文件标识序列和文件大小序列，求解采用合理的缓存策略，最少需要的金币数。
输入描述
第一行为缓存一个报告金币数M，L<=M<=100
第二行为文件标识序列：F1,F2,F3…Fn。
第三行为文件大小序列：
相关文章：
【华为OD机试2023】静态扫描 C++ Java Python
【华为OD机试2023】静态扫描 C++ Java Python 前言 如果您在准备华为的面试，期间有想了解的可以私信我，我会尽可能帮您解答，也可以给您一些建议！ 本文解法非最优解（即非性能最优），不能保证通过率。 Tips1：机试为ACM 模式 你的代码需要处理输入输出，input/cin接收输入、…...
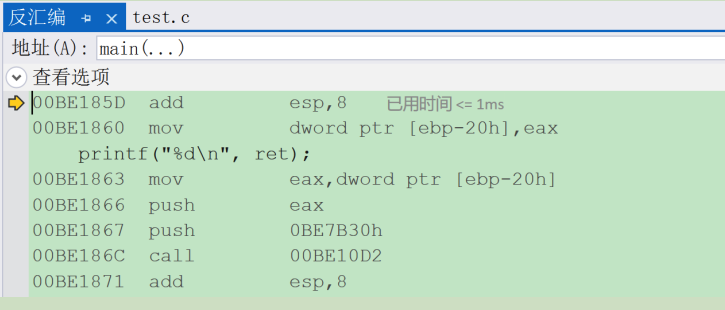
函数栈帧的创建和销毁（详解）
函数栈帧的创建和销毁🦖函数栈帧是什么？🦖函数栈帧的创建和销毁解析🐋栈是什么？🐋认识相关寄存器和汇编指令🐋解析函数栈帧的创建和销毁🐳预备知识🐳函数的调用堆栈&…...
【100个 Unity实用技能】 | 脚本无需挂载到游戏对象上也可执行的方法
Unity 小科普 老规矩，先介绍一下 Unity 的科普小知识： Unity是 实时3D互动内容创作和运营平台 。包括游戏开发、美术、建筑、汽车设计、影视在内的所有创作者，借助 Unity 将创意变成现实。Unity 平台提供一整套完善的软件解决方案ÿ…...
条件期望5
条件期望例题 随机图 从节点1开始, N为一个随机变量, 表示整个过程第一次出现"贪吃蛇"情形时, 所进行的步数.即Nk⇒Xk(1)∈{1,X(1),X2(1),...Xk−1(1)}其中1,X(1),X2(1),...Xk−1(1)各不相同N k \Rightarrow X^k(1) \in \{1,X(1), X^2(1),...X^{k-1}(1)\} \\ 其中1…...
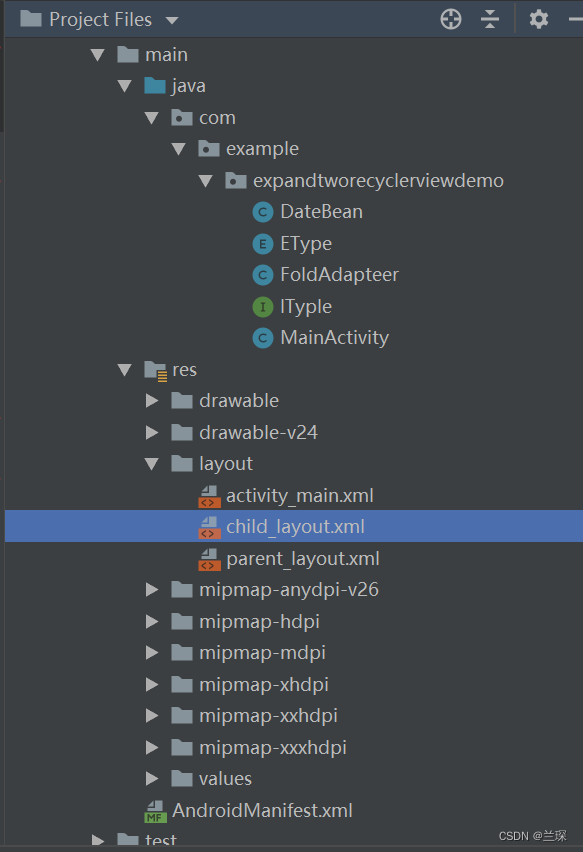
RecyclerView ViewType二级
实现效果描述： 1、点击recyclerview中item，列表下方出现其他样式的item，作为子item，如下所示 所需要的java文件和xml文件有： 1、创建FoldAdapteradapter, 在FoldAdapter中，定义两种不同的类型ÿ…...
将对象或数组存在 dom元素的属性上，最后取不到完整数据，只取到 [{
目录 一、问题 二、问题及解决方法 三、总结 一、问题 1.我需要在dom元素里面添加了一个属性test存一个对象数组temp，以便我下一次找到这个dom元素时可以直接拿到属性里面的数据来渲染页面。 2.dom 属性上存 对象和数组，必须先JSON.stringify(arr),转…...
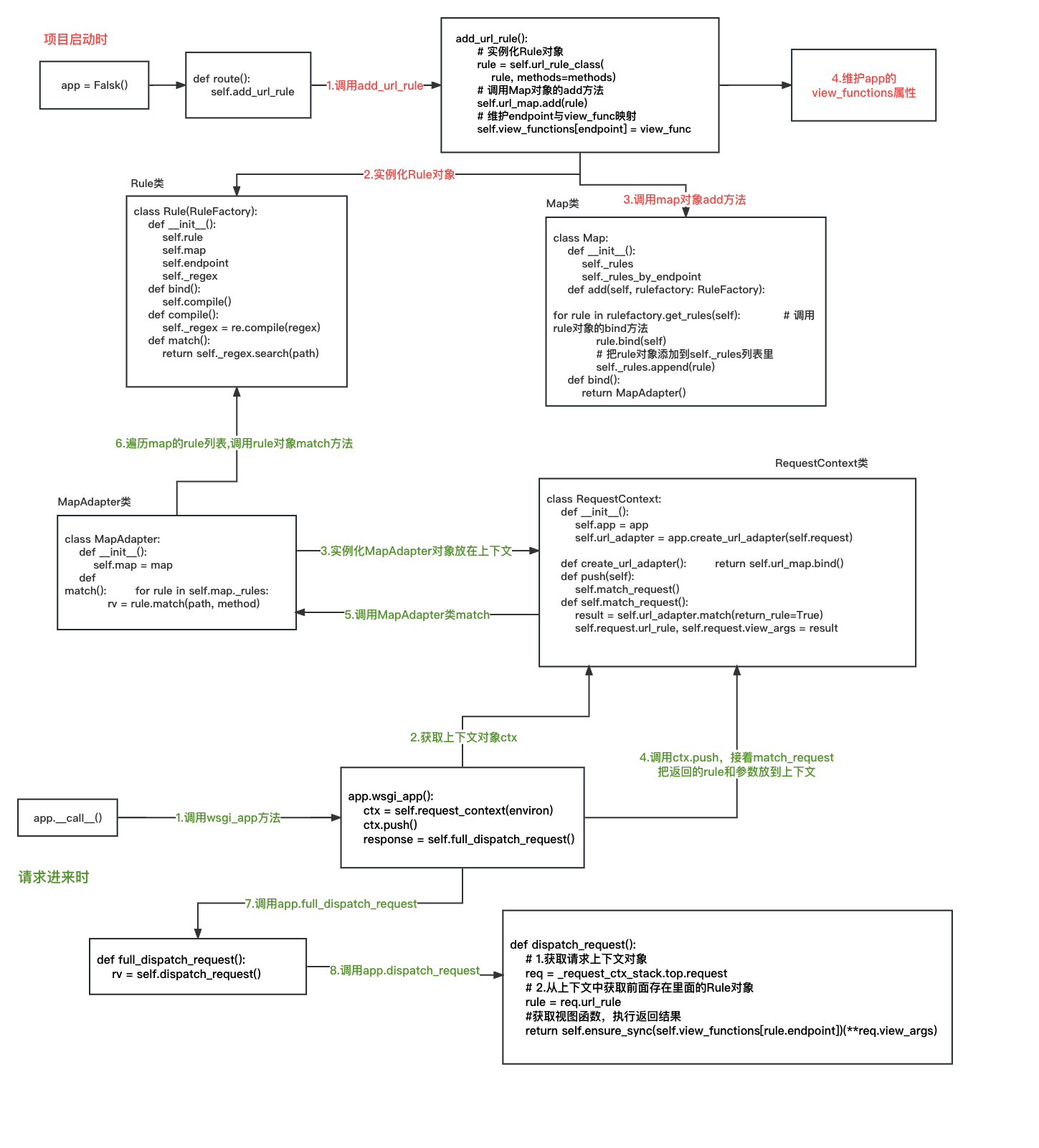
Flask源码篇：Flask路由规则与请求匹配过程（超详细，易懂）
目录1 启动时路由相关操作（1）分析app.route()（2）分析add_url_rule()（3）分析Rule类（4）分析Map类（5）分析MapAdapter类（6）分析 url_rule_…...
Jmeter接口测试教程之【参数化技巧总结】，总有一个是你不知道的
目录：导读 一、随机值 二、随机字符串 三、时间戳 四、唯一字符串UUID 说起接口测试，相信大家在工作中用的最多的还是Jmeter。 大家看这个目录就知道jmeter的应用有多广泛了：https://www.bilibili.com/video/BV1e44y1X78S/? JMeter是一个…...
缓存与数据库的双写一致性
背景 在高并发的业务场景下，系统的性能瓶颈往往是出现在数据库上，用户并发访问过大，压力都打到数据库上。所以一般都会用redis做缓存层，起到一个缓冲作用，让请求先访问到缓存层，而不是直接去访问数据库&am…...
)
力扣-213打家劫舍II(dp)
力扣-213打家劫舍II 1、题目 213. 打家劫舍 II 你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通…...
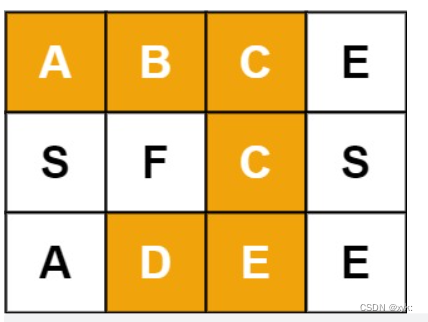
关于【网格结构】岛屿类问题的通用解法DFS（深度遍历）遍历框架+回溯+剪枝总结
最近在刷力扣时遇见的问题，自己总结加上看了力扣大佬的知识总结写下本篇文章，我们所熟悉的 DFS（深度优先搜索）问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题，是在一种「网格」结构中进行的。岛屿问题…...
【LeetCode】982. 按位与为零的三元组
982. 按位与为零的三元组 题目描述 给你一个整数数组 nums ，返回其中 按位与三元组 的数目。 按位与三元组 是由下标 (i, j, k) 组成的三元组，并满足下述全部条件： 0 < i < nums.length0 < j < nums.length0 < k < num…...
Linux内核源码进程原理分析
Linux内核源码进程原理分析一、Linux 内核架构图二、进程基础知识三、Linux 进程四要素四、task_struct 数据结构主要成员五、创建新进程分析六、剖析进程状态迁移七、写时复制技术一、Linux 内核架构图 二、进程基础知识 Linux 内核把进程称为任务(task)，进程的虚…...
电子技术——CMOS反相器
电子技术——CMOS反相器 在本节，我们深入学习CMOS反相器。 电路原理 下图是我们要研究的CMOS反相器的原理图： 下图展示了当输入 vIVDDv_I V_{DD}vIVDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线： 我们把 QNQ_NQN 当做是驱动源&#x…...
gazebo仿真轨迹规划+跟踪（不在move_base框架下）
以Tianbot为例子，开源代码如下： https://github.com/tianbot/tianbot_mini GitHub - tianbot/abc_swarm: Ant Bee Cooperative Swarm, indicating air-ground cooperation. This repository is for Tianbot Mini and RoboMaster TT swarm kit. 1.在…...
C. Good Subarrays（前缀和）
C. Good Subarrays一、问题二、分析三、代码一、问题 二、分析 这道题目的意思就是给我们一个数组，然后我们从数组中选取一个连续的区间，这个区间满足条件：区间内的元素和等于区间的长度。 对于区间和问题我们先想到的是前缀和的算法。 那…...
关于Facebook Messenger CRM，这里有你想要知道的一切
关于Facebook Messenger CRM，这里有你想要知道的一切！想把Facebook Messenger与你的CRM整合起来吗？这篇博文是为你准备的! 我们将介绍有关获得Facebook Messenger CRM整合的一切信息。然后，我们将解释为什么你需要像SaleSmartly&a…...
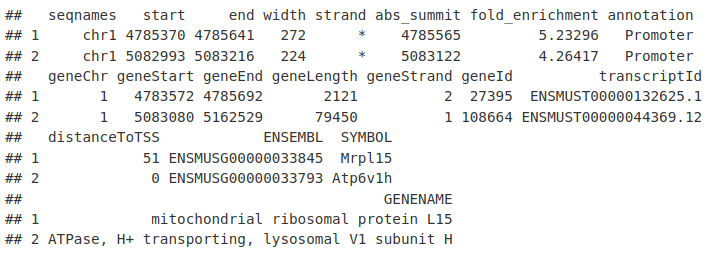
ChIP-seq 分析：数据与Peak 基因注释（10）
动动发财的小手，点个赞吧！ 1. 数据 今天，我们将继续回顾我们在上一次中研究的 Myc ChIPseq。这包括用于 MEL 和 Ch12 细胞系的 Myc ChIPseq。 可在此处[1]找到 MEL 细胞系中 Myc ChIPseq 的信息和文件可在此处[2]找到 Ch12 细胞系中 Myc ChIP…...
《C++ Primer Plus》第18章：探讨 C++ 新标准（8）
使用大括号括起的初始化列表语法重写下述代码。重写后的代码不应使用数组 ar： class Z200 { private:int j;char ch;double z; public:Z200(int jv, char chv, zv) : j(jv), ch(chv), z(zv) {} ... };double x 8.8; std::string s "What a bracing effect!&q…...
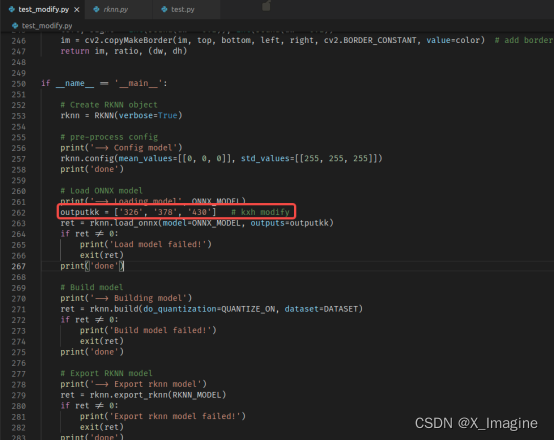
YOLO-V5 系列算法和代码解析（八）—— 模型移植
文章目录工程目标芯片参数查阅官方文档基本流程Python 版工具链安装RKNPU2的编译以及使用方法移植自己训练的模型工程目标 将自己训练的目标检测模型【YOLO-V5s】移植到瑞芯微【3566】芯片平台，使用NPU推理，最终得到正确的结果。整个过程涉及模型量化、…...
[2025CVPR]DeepVideo-R1：基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈，在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度，导致： 梯度抑制：当新旧策略差异过大时梯度消失收敛困难：策略无法充分优化# 传统GRPO的梯…...
Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明：server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
【OSG学习笔记】Day 16: 骨骼动画与蒙皮（osgAnimation）
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术，它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton)：由层级结构的骨头组成，类似于人体骨骼蒙皮 (Mesh Skinning)：将模型网格顶点绑定到骨骼上，使骨骼移动…...
[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法，且在 O(n) 时间复杂度…...
图表类系列各种样式PPT模版分享
图标图表系列PPT模版，柱状图PPT模版，线状图PPT模版，折线图PPT模版，饼状图PPT模版，雷达图PPT模版，树状图PPT模版 图表类系列各种样式PPT模版分享：图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
【Oracle】分区表
个人主页：Guiat 归属专栏：Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
Angular微前端架构：Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例，其中使用的是 Module Federation 和 npx-build-plus 实现了主应用（Shell）与子应用（Remote）的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知，帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量，能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度，还为机器人、医疗设备和制造业的智…...
MySQL的pymysql操作
本章是MySQL的最后一章，MySQL到此完结，下一站Hadoop！！！ 这章很简单，完整代码在最后，详细讲解之前python课程里面也有，感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
阿里云Ubuntu 22.04 64位搭建Flask流程（亲测）
cd /home 进入home盘 安装虚拟环境： 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境： virtualenv myenv 3、激活虚拟环境（激活环境可以在当前环境下安装包） source myenv/bin/activate 此时，终端…...