数据结构奇妙旅程之二叉树初阶
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏:xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!

一.树
1.概念(简单了解即可)
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
2.树的基本术语

2.1需要重点记忆的
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为3
2.2简单了解即可
3.树的代码表示形式(简单了解)
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,
class Node {
int value; // 树中存储的数据
Node firstChild; // 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}二.二叉树(重点掌握)
1.概念
一棵二叉树是结点的一个有限集合,该集合:

1.1二叉树的基本形态

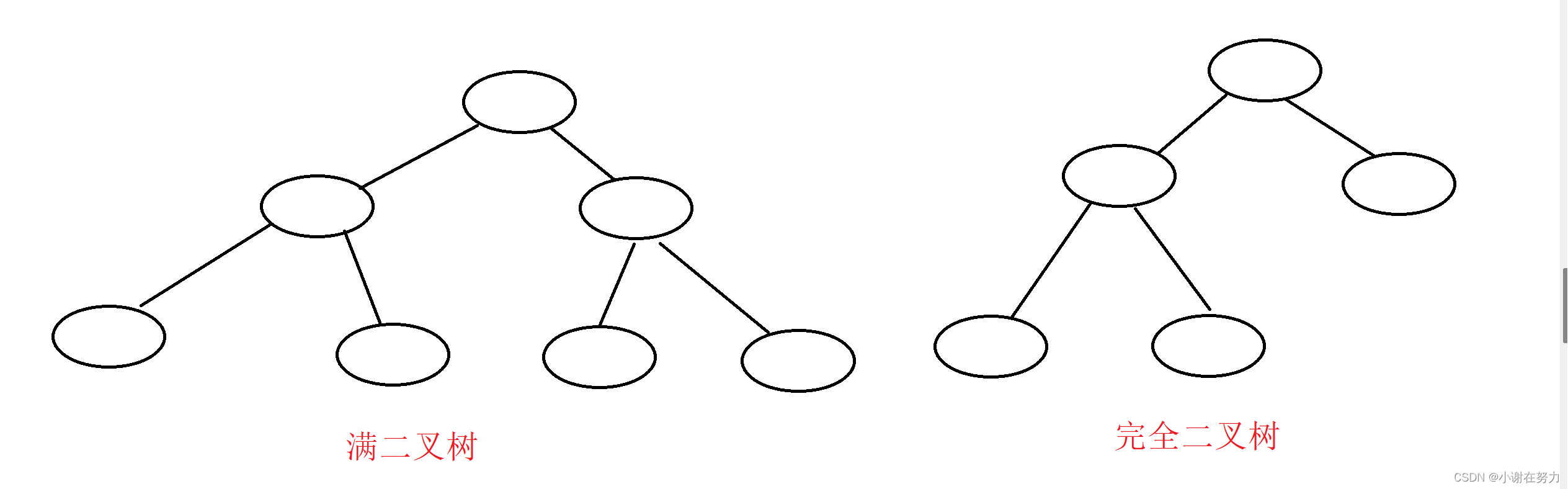
1.2两种特殊的二叉树
2.性质
3.基本操作
public class BinaryTree {static class TreeNode {public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}}//以穷举的方式 创建一棵二叉树出来public TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;return A;}//前序遍历public void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(TreeNode root) {if(root == null){return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}//后序遍历public void postOrder(TreeNode root) {if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}// 获取二叉树中节点的个数public int size(TreeNode root) {if(root == null) {return 0;}return size(root.left)+size(root.right)+1;}// 获取叶子节点的个数public int getLeafNodeCount(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}// 获取第K层节点的个数public int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);}// 获取二叉树的高度public int getHeight(TreeNode root) {if(root == null) {return 0;}int leftH = getHeight(root.left);int rightH = getHeight(root.right);return Math.max(leftH,rightH)+1;}// 检测值为value的元素是否存在public boolean find(TreeNode root,char val) {if(root == null) {return false;}if(root.val == val) {return true;}return find(root.left, val) || find(root.right, val);}//层序遍历使用队列来辅助//当涉及到层序遍历时,通常情况下使用队列来实现会更为简单和高效public void levelOrder(TreeNode root) {if(root == null) {return;}Queue<TreeNode> q = new LinkedList<>();q.offer(root);while (!q.isEmpty()) {TreeNode cur = q.poll();System.out.print(cur.val + " ");if(cur.left != null) {q.offer(cur.left);}if(cur.right != null) {q.offer(cur.right);}}}// 判断一棵树是不是完全二叉树public boolean isCompleteTree(TreeNode root) {if (root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);boolean end = false;while (!queue.isEmpty()) {TreeNode current = queue.poll();if (current == null) {end = true;} else {if (end) {return false; // 如果已经遇到空节点,再遇到非空节点,说明不是完全二叉树}queue.offer(current.left);queue.offer(current.right);}}return true;}
}
三.说明
以上就是关于二叉树的一些基础问题了,如果你已经对这些比较基础的问题都大概了解,就可以开始尝试做题,你也可以移步到博主的下一篇关于二叉树面试题的文章,帮助你更好的掌握二叉树,感谢你的观看,愿你一天开心愉快
相关文章:
数据结构奇妙旅程之二叉树初阶
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...
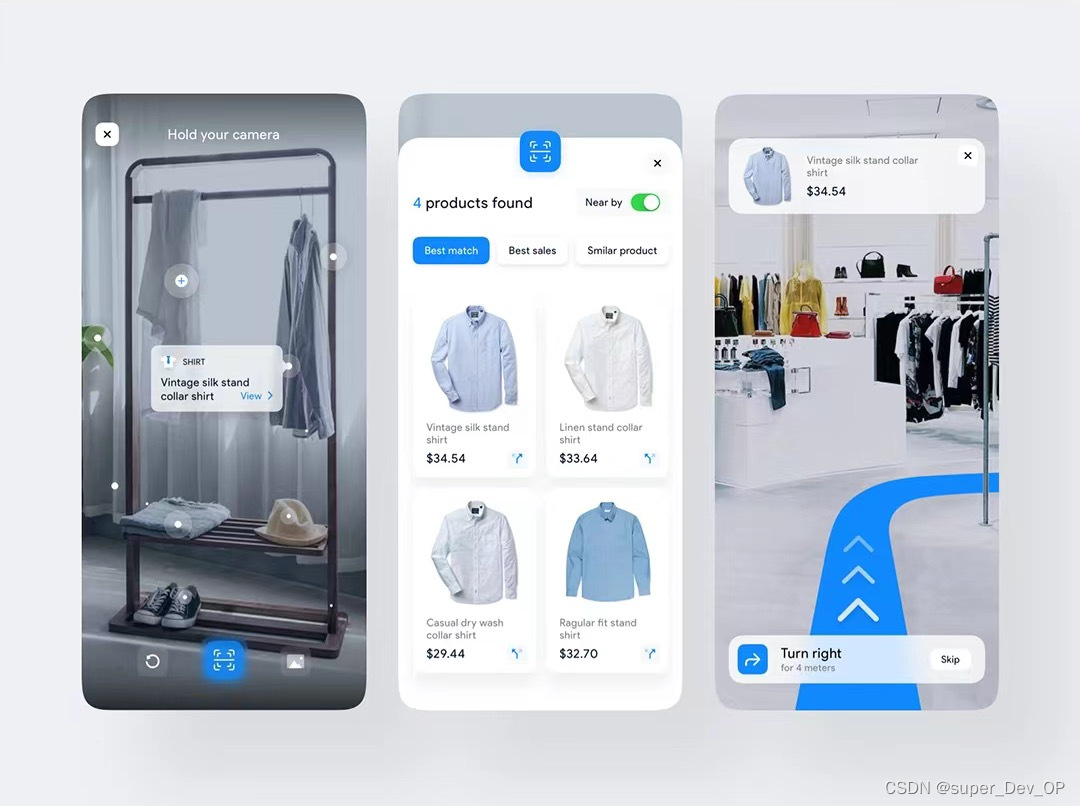
WebGL中开发VR(虚拟现实)应用
WebGL(Web Graphics Library)是一种用于在浏览器中渲染交互式3D和2D图形的JavaScript API。要在WebGL中开发VR(虚拟现实)应用程序,您可以遵循以下一般步骤,希望对大家有所帮助。北京木奇移动技术有限公司&a…...

elemeentui el-table封装
elemeentui el-table封装 <template><div style"height: 100%;"><el-table ref"sneTable" element-loading-text"加载中" element-loading-spinner"el-icon-loading"element-loading-background"rgba(45,47,79…...

openssl3.2 - 官方demo学习 - guide - quic-client-block.c
文章目录 openssl3.2 - 官方demo学习 - guide - quic-client-block.c概述笔记END openssl3.2 - 官方demo学习 - guide - quic-client-block.c 概述 在程序运行时, 要指定环境变量 SSL_CERT_FILErootcert.pem, 同时将rootcert.pem拷贝到工程目录下, 否则不好使 吐槽啊, 为啥不…...

滑动窗口经典入门题-——长度最小子数组
文章目录 算法原理题目解析暴力枚举法的代码优化第一步初始化第二步right右移第三步left右移 滑动窗口法的代码 算法原理 滑动窗口是一种在序列(例如数组或链表)上解决问题的算法模式。它通常用于解决子数组或子字符串的问题,其中滑动窗口表示…...

AcGeMatrix2d::alignCoordSys一种实现方式
问题描述 此处为了简化问题,在2维空间中处理,按以下方式调用,AcGeMatrix2d::alignCoordSys是如何求出一个矩阵的呢,这里提供一个实现思路(但效率不保证好) AcGeMatrix2d matTrans AcGeMatrix2d::alignCo…...
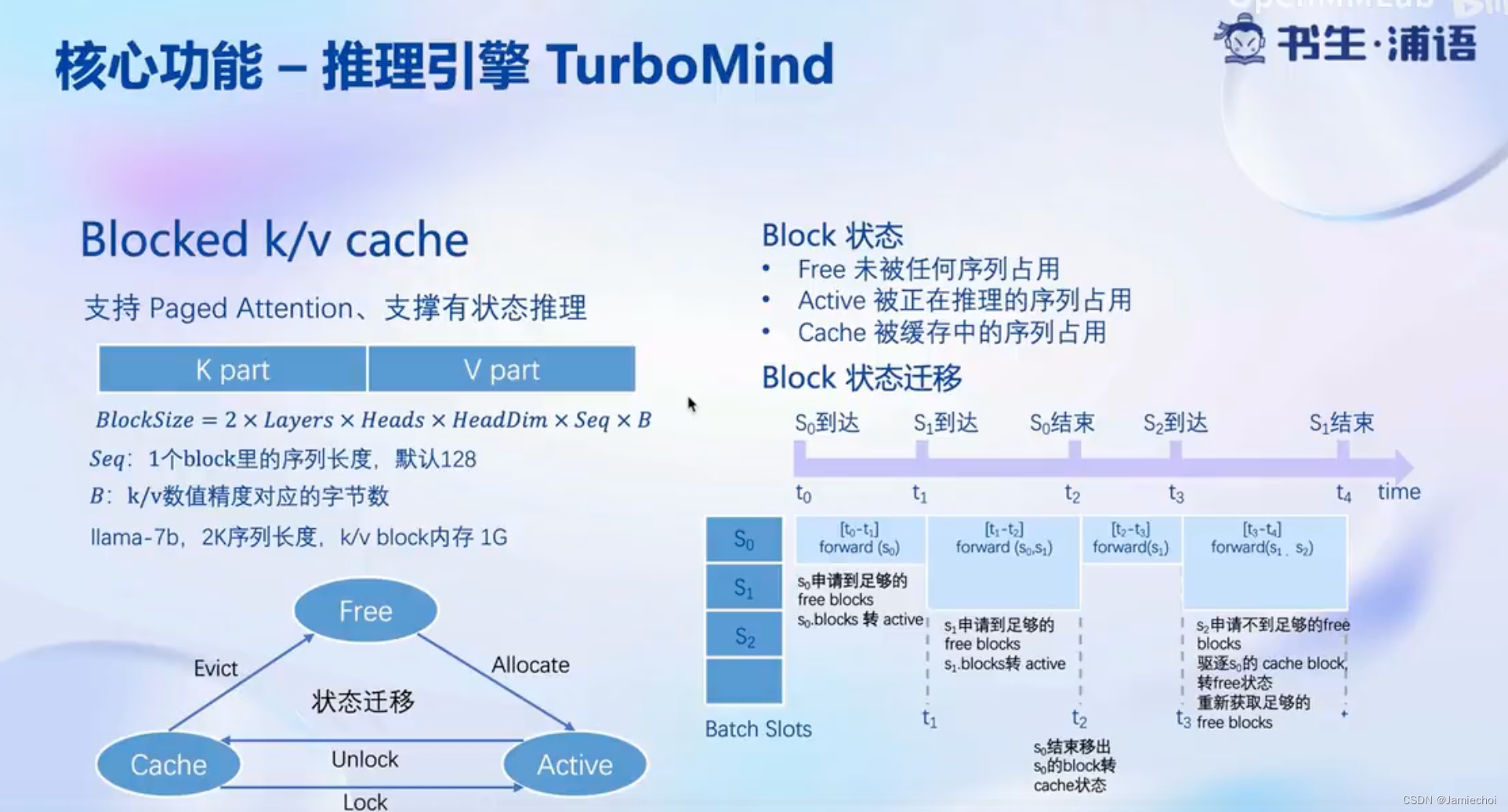
InternLM第5次课笔记
LMDeploy 大模型量化部署实践 1 大模型部署背景 2 LMDeploy简介 3 动手实践环节 https://github.com/InternLM/tutorial/blob/main/lmdeploy/lmdeploy.md 3...

2018年认证杯SPSSPRO杯数学建模D题(第一阶段)投篮的最佳出手点全过程文档及程序
2018年认证杯SPSSPRO杯数学建模 对于投篮最佳出手点的探究 D题 投篮的最佳出手点 原题再现: 影响投篮命中率的因素不仅仅有出手角度、球感、出手速度,还有出手点的选择。规范的投篮动作包含两膝微屈、重心落在两脚掌上、下肢蹬地发力、身体随之向前上…...
使用pdfbox 为 PDF 增加水印
使用pdfbox 为 PDF增加水印https://www.jylt.cc/#/detail?activityIndex2&idbd410851b0a72dad3105f9d50787f914 引入依赖 <dependency><groupId>org.apache.pdfbox</groupId><artifactId>pdfbox</artifactId><version>3.0.1</ve…...

6.【CPP】Date类的实现
Date.h #pragma once using namespace std; #include<iostream>class Date {friend ostream& operator<<(ostream& out, const Date& d);friend istream& operator>>(istream& in, Date& d); public://构造函数会被频繁调用,放在类…...
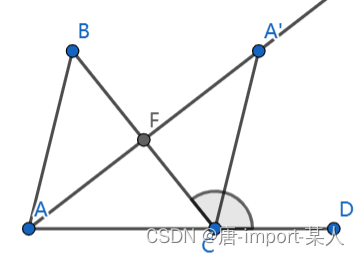
三角形任意一外角大于不相邻的任意一内角
一.代数证明 ∵ 对与△ A C B 中 ∠ c 外接三角形是 ∠ B C D ∵对与△ACB中∠c外接三角形是∠BCD ∵对与△ACB中∠c外接三角形是∠BCD ∴ ∠ B C D π − ∠ C ∴∠BCD\pi-∠C ∴∠BCDπ−∠C ∵ ∠ A ∠ B ∠ C π ∵∠A∠B∠C\pi ∵∠A∠B∠Cπ ∴ ∠ B C D ∠ A ∠…...

【Spring Boot 3】【Redis】集成Lettuce
【Spring Boot 3】【Redis】集成Lettuce 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总是要花…...
【SQL注入】SQLMAP v1.7.11.1 汉化版
下载链接 【SQL注入】SQLMAP v1.7.11.1 汉化版 简介 SQLMAP是一款开源的自动化SQL注入工具,用于扫描和利用Web应用程序中的SQL注入漏洞。它在安全测试领域被广泛应用,可用于检测和利用SQL注入漏洞,以验证应用程序的安全性。 SQL注入是一种…...
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤)
时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤) 目录 时序预测 | MATLAB实现GRNN广义回归神经网络时间序列未来多步预测(程序含详细预测步骤)预测效果基本介绍程序设计参考资料预测效果 基本介绍 MATLAB实现GRNN广义回归神经网络时间序列…...

长期戴耳机的危害有哪些?戴哪种耳机不伤耳朵听力?
长期佩戴耳机可能会出现听力下降、耳道感染等危害。 听力下降:长时间戴耳机可能会导致耳道内的声音过大,容易对耳膜造成一定的刺激,容易出现听力下降的情况。 耳道感染:长时间戴耳机,耳道长期处于封闭潮湿的情况下&a…...

C++中的预处理
一.预定义符号 1.__FILE__进行编译的源文件 2.__LINE__文件当前的行号 3.__DATE__文件被编译的日期 4.__TIME文件被编译的时间 5.__STDC__如果编译器遵循ANSIC,其值为1,否则未定义 二.#define 基本语法:#define 名字 内容 eg.define M 1 经#define定义的常量时不经过…...
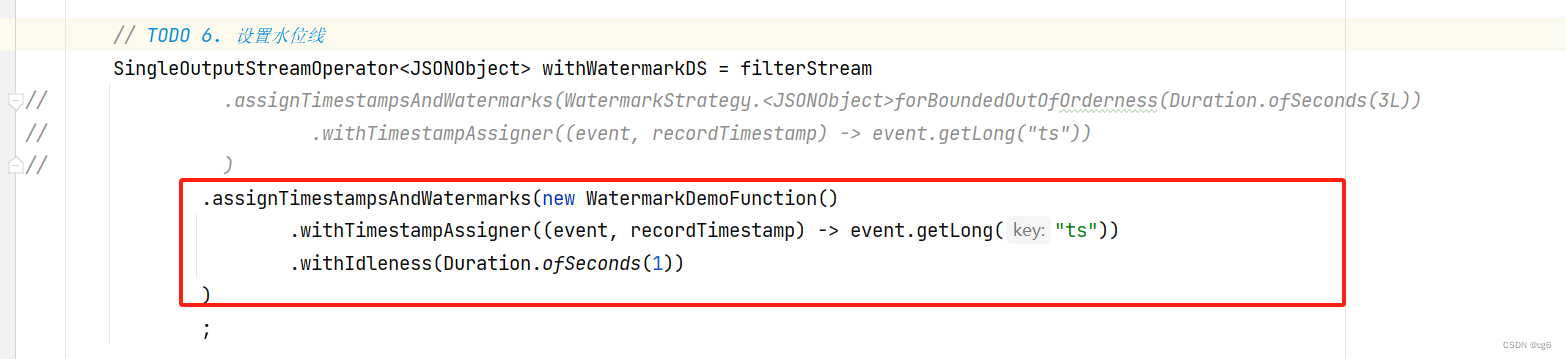
flink 最后一个窗口一直没有新数据,窗口不关闭问题
flink 最后一个窗口一直没有新数据,窗口不关闭问题 自定义实现 WatermarkStrategy接口 自定义实现 WatermarkStrategy接口 窗口类型:滚动窗口 代码: public static class WatermarkDemoFunction implements WatermarkStrategy<JSONObject…...

mybatis----小细节
1、起别名 在MyBatis中,<typeAliases>元素用于定义类型别名,它可以将Java类名映射为一个更简短的别名,这样在映射文件中可以直接使用别名而不需要完整的类名。 下面是一个示例: 在mybatis核心配置文件中配置typeAliases标…...

解密Oracle数据库引擎:揭开数据存储的神秘面纱
目录 1、介绍Oracle数据库引擎 1.1 什么是Oracle数据库引擎 1.2 Oracle数据库引擎的作用和功能 1.3 Oracle数据库引擎的历史和发展 2、Oracle数据库引擎的体系结构 2.1 Oracle数据库实例的组成部分 2.2 Oracle数据库引擎的层次结构 2.3 Oracle数据库引擎的关键组件 3、…...

「HDLBits题解」Karnaugh Map to Circuit
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 相关资料:卡诺图化简法-CSDN博客 题目链接:Kmap1 - HDLBits module top_module(input a,input b,input c,output out );assig…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
