vue2+webpack升级vue3+vite,报错Cannot read properties of null (reading ‘isCE‘)
同学们可以私信我加入学习群!
正文开始
- 前言
- 问题
- 分析
- 解决
- 总结
前言
系列文章:vue2+webpack升级vue3+vite,修改插件兼容性bug
前面的文章主要是介绍,在升级初始阶段遇到的一些显而易见的兼容性问题和bug。随着项目迭代的不断深入,一些不容易暴露的问题也渐渐呈现。
本文主要记录一些开发重构过程中的bug
问题
vue报错Cannot read properties of null (reading ‘isCE’)
分析
项目中vue版本出现冲突,可能是项目基础的vue版本与组件库中某个组件依赖的vue版本有冲突。但是我怀疑这只是表象,因为如果存在版本冲突,那么第一天就存在,为什么后面才暴露。而且使用npm列出所有vue版本发现并没有冲突的版本。所以最终虽然解决了,但是总觉得还是不太清楚。
解决
- 命令行中输入
npm ls vue
可以查看所有vue的版本,如图:
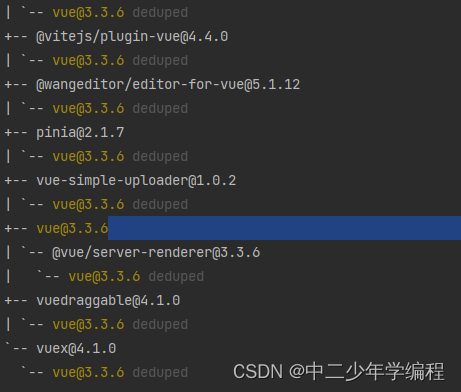
如果各位使用脚手架创建的项目,vue的版本会设置‘^’符号,例如我的设置为:
"vue": "^3.3.4",
大家可以看到package.json中设置的版本号与实际项目中依赖的vue版本并不完全相同,这是因为^符号的含义就是保持大版本不变,可以根据兼容性等实际情况,升级小版本,所以 ’ ^3.3.4’的真实含义是3.3.4及以上版本,这样其实很难真的出现vue版本冲突的情况。通过上面的图片也可以知道,我的所有插件都是依赖于3.3.6。
实际情况确实是报错vue版本冲突,所以我只能认为可能是因为别的原因导致了这个报错,也就是其实报错信息就有问题。我没有想到其他方法严谨地定位到问题,只能把可以做的都做了一遍。
- 升级node
看一下自己的node版本,vue2在16版本的node中运行毫无问题,vue3在部分16版本的node中也无太大问题,但是总会出现预料不到的风险,甚至升级某些插件时也会提示node版本过低。vue官网也推荐18版本以上node:
所以为了省事,还是直接升级node吧。
这里有个问题,那就是18版本的node可能运行vue2时会报错,所以如果是升级vue,可能会有一段时间,既开发vue2,又重构vue3,我们就需要一个很方便的node版本管理工具,推荐nvm。我自己写的基于nvm的可视化工具也快要完成了,基本功能已经实现,还达不到生产标准。
大家可以提前关注一波,等几个重要的工具同时开发完毕,会免费发布并群发消息提醒。如图:
- 虽然大概率不是vue版本的问题,但是为了以防万一,还是对vue版本做一个强制限制吧,在vite中配置参数dedupe,解决vue版本依赖冲突问题:
resolve: {dedupe: ['vue'],},
- 如果这些还是无法解决,那就先清楚npm的缓存:
npm cache clean --force
删除node_modules后,重新更新资源,运行项目。
总结
博主的大部分文章都是有价值的原创文章,很少搬运点官方文档就水一篇,大家如果认可,希望多多点赞关注,原创不易,需要支持。
相关文章:

vue2+webpack升级vue3+vite,报错Cannot read properties of null (reading ‘isCE‘)
同学们可以私信我加入学习群! 正文开始 前言问题分析解决总结 前言 系列文章:vue2webpack升级vue3vite,修改插件兼容性bug 前面的文章主要是介绍,在升级初始阶段遇到的一些显而易见的兼容性问题和bug。随着项目迭代的不断深入&a…...

【性能调优】local模式下flink处理离线任务能力分析
文章目录 一. flink的内存管理1.Jobmanager的内存模型2.TaskManager的内存模型2.1. 模型说明2.2. 通讯、数据传输方面2.3. 框架、任务堆外内存2.4. 托管内存 3.任务分析 二. 单个节点的带宽瓶颈1. 带宽相关理论2. 使用speedtest-cli 测试带宽3. 任务分析3. 其他工具使用介绍 本…...

Zabbix监控(2)
目录 一.自动发现 配置自动发现:(被动模式) 修改三台服务器的hosts文件: 修改agent02的配置文件: 访问页面,删除客服端主机配置: 在配置的自动发现中添加规则: 我们重启的zab…...
uni-app中代理的两种配置方式
方式一: 在项目的 manifest.json 文件中点击 源码视图 在最底部的vue版本下编写代理代码 方式二: 在项目中创建 vue.config.js 文件然后进行配置 在页面中发起请求 完整的url:http://c.m.163.com/recommend/getChanListNews?channelT1457068979049&size10 …...
循环异步调取接口使用数组promiseList保存,Promise.all(promiseList)获取不到数组内容,then()返回空数组
在使用 vue vant2.13.2 技术栈的项目中,因为上传文件的接口是单文件上传,当使用批量上传时,只能循环调取接口;然后有校验内容:需要所有文件上传成功后才能保存,在文件上传不成功时点击保存按钮,…...

C++轮子 · STL 序列容器
STL中大家最耳熟能详的可能就是容器,容器大致可以分为两类,序列型容器(SequenceContainer)和关联型容器(AssociativeContainer)这篇文章中将会重点介绍STL中的各种序列型容器和相关的容器适配器。主要内容包括 std::vectorstd::arraystd::dequestd::queuestd::stackstd::…...
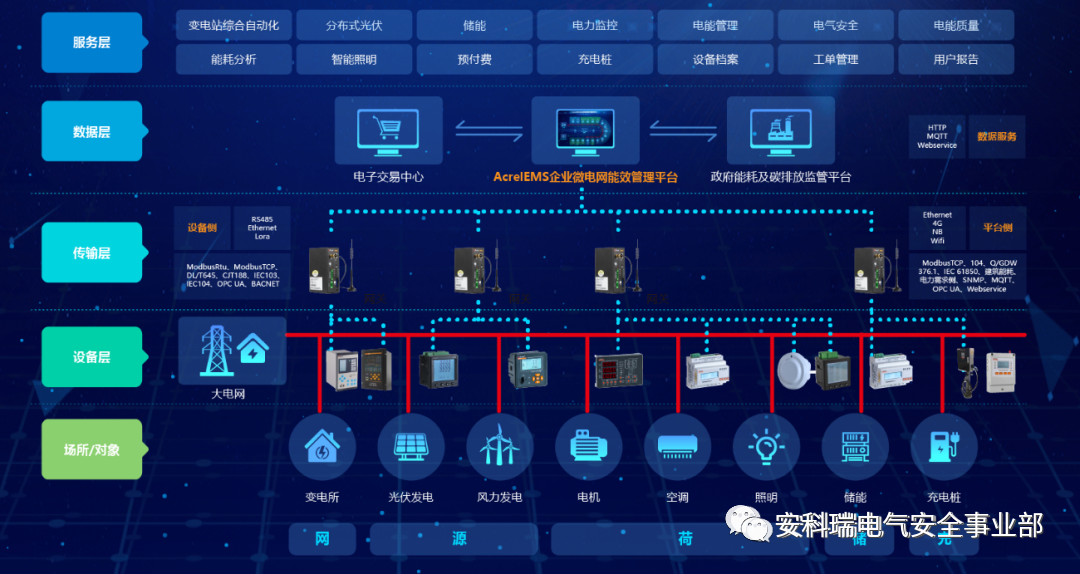
浅谈智慧路灯安全智能供电方案设计
摘要: 智慧路灯,作为智慧城市、新基建、城市更新的主要组成部分,近些年在各大城市已得到很好的落地和 应用,但其与传统路灯相比集成大量异元异构电子设备,这些设备的供电电压、接口形式、权属单位各不相同, 如何设计一…...
:工厂方法模式)
C#设计模式教程(2):工厂方法模式
工厂方法模式是一种创建型设计模式,它定义了一个用于创建对象的接口,但让子类决定实例化哪一个类。工厂方法使一个类的实例化延迟到其子类。 C# 代码实现 以下是C#中实现工厂方法模式的一个简单示例: 首先,定义一个抽象产品(Product)类,它是所有具体产品的基类。 pu…...

程序员的能力-如何成为不会过时的“码农”
码农是指从事编程工作的人,也被称为程序员或开发者。他们使用计算机语言和工具来编写、测试和维护软件程序或网站。码农通常需要具备扎实的计算机科学知识、编程技能和问题解决能力,以及良好的逻辑思维和团队合作能力。他们可以在软件开发公司、科技企业…...
【OpenAI】自定义GPTs应用(GPT助手应用)及外部API接口请求
11月10日,OpenAI正式宣布向所有ChatGPT Plus用户开放GPTs功能 简而言之:GPT应用市场(简称GPTs, 全称GPT Store) Ps: 上图为首次进入时的页面,第一部分是自己创建的GPTs应用,下面是公开可以使用的GPTs应用 一、创建GPTs…...

canvas绘制不同样式的五角星(图文示例)
查看专栏目录 canvas实例应用100专栏,提供canvas的基础知识,高级动画,相关应用扩展等信息。canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重…...

C#: BitConverter 字节数组byte[ ] 转各种数据类型用法列举
说明:C# BitConverter 字节数组byte[ ] 转各种数据类型用法示例 1.ToBoolean(byte[] value, int startIndex):将指定字节数组中从指定索引开始的两个字节转换为布尔值。 byte[] bytes { 1, 0 }; bool result BitConverter.ToBoolean(bytes, 0); // 输…...

【开发实践】前端jQuery+gif图片实现载入界面
一、需求分析 载入界面(Loading screen)是指在计算机程序或电子游戏中,当用户启动应用程序或切换到新的场景时,显示在屏幕上的过渡界面。它的主要作用是向用户传达程序正在加载或准备就绪的信息,以及提供一种视觉上的反…...

解析消费全返:谈谈那些关于商业的小妙招
每天五分钟讲解商业模式,大家好我是模式策划啊浩。 在数字化时代,商业模式正在经历前所未有的变革。其中,消费全返的概念正在逐渐崭露头角,引领着商业创新的新潮流。消费全返,顾名思义,是指消费者在购买商…...
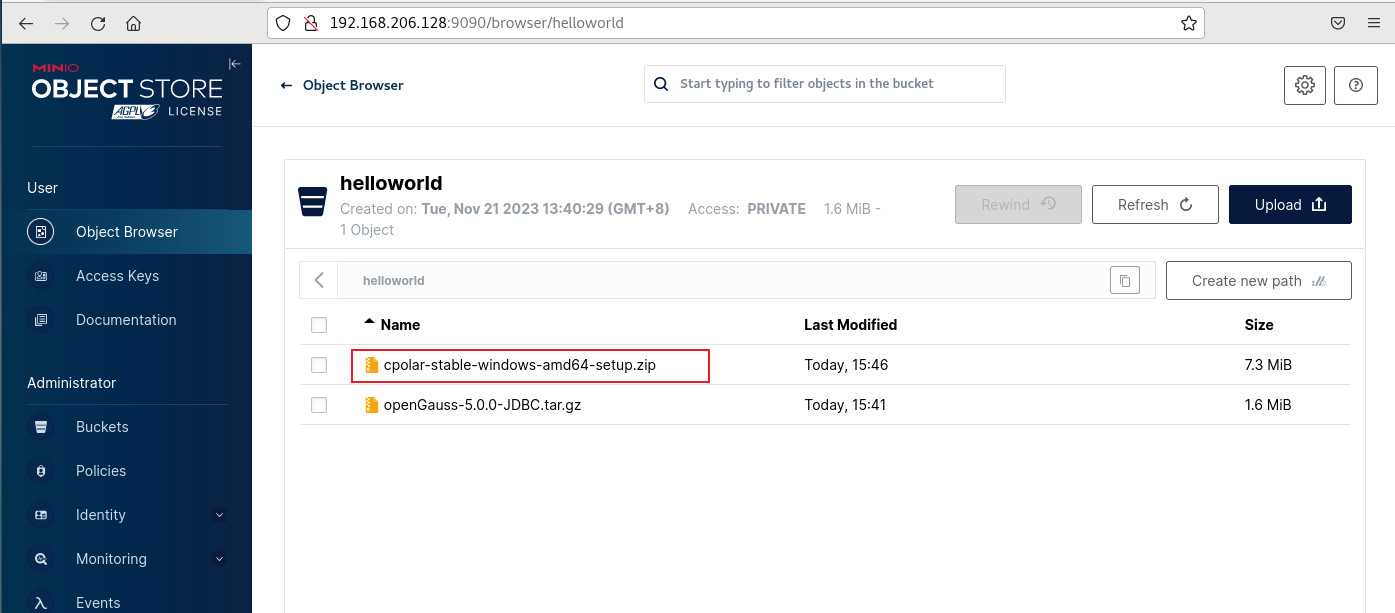
如何在MinIO存储服务中通过Buckets实现远程访问管理界面上传文件
文章目录 前言1. 创建Buckets和Access Keys2. Linux 安装Cpolar3. 创建连接MinIO服务公网地址4. 远程调用MinIO服务小结5. 固定连接TCP公网地址6. 固定地址连接测试 前言 MinIO是一款高性能、分布式的对象存储系统,它可以100%的运行在标准硬件上,即X86等…...

算法 - 二分法 / 双指针 / 三指针 / 滑动窗口
文章目录 🍺 二分法🍻 旋转数组🥂 33. 搜索旋转排序数组 [旋转数组] [目标值] (二分法) 🍻 元素边界🥂 34. 在排序数组中查找元素的第一个和最后一个位置 [有序数组] > [元素边界] > (二分法)🥂 81. …...

ChatGPT3.5、GPT4.0、DALL·E 3和Midjourney对话与绘画智能体验
MidTool(https://www.aimidtool.com/)是一个集成了多种先进人工智能技术的助手,它融合了ChatGPT3.5、GPT4.0、DALLE 3和Midjourney等不同的智能服务,提供了一个多功能的体验。下面是这些技术的简要介绍: ChatGPT3.5&am…...

MySQL中锁的概述
按照锁的粒度来分可分为:全局锁(锁住当前数据库的所有数据表),表级锁(锁住对应的数据表),行级锁(每次锁住对应的行数据) 加全局锁:flush tables with read lo…...

5396. 棋盘
5396. 棋盘 - AcWing题库 二维差分数组 #include <iostream> #include <vector> using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> v(n 2, vector<int>(n 2));while (m--) {int x1, x2, y1, y2;cin…...
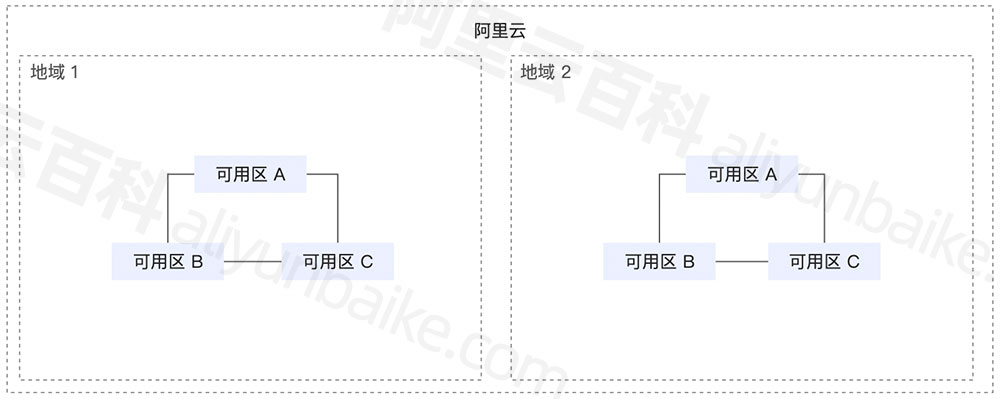
阿里云地域和可用区分布表,2024更新
2024年阿里云服务器地域分布表,地域指数据中心所在的地理区域,通常按照数据中心所在的城市划分,例如华北2(北京)地域表示数据中心所在的城市是北京。阿里云地域分为四部分即中国、亚太其他国家、欧洲与美洲和中东&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
