20240119-子数组最小值之和
题目要求
给定一个整数数组 arr,求 min(b) 的总和,其中 b 的范围涵盖 arr 的每个(连续)子数组。由于答案可能很大,因此返回答案模数
Example 1:
Input: arr = [3,1,2,4] Output: 17 Explanation: Subarrays are [3], [1], [2], [4], [3,1], [1,2], [2,4], [3,1,2], [1,2,4], [3,1,2,4]. Minimums are 3, 1, 2, 4, 1, 1, 2, 1, 1, 1. Sum is 17.
Example 2:
Input: arr = [11,81,94,43,3] Output: 444
思路
找出数组的全部组合数,加和并返回mod()之后的结果。我们只需要找出所有的组合然后加到一起。但是这样至少需要O(N^2)的时间复杂度,会超时。
然后又想到不需要真正求出子数组,只需要求出子数组的最小值即可。同时发现子数组不能交换顺序。因此想到用单调栈解决本题。
-
左侧范围:我们需要找出在
arr[i]左侧的第一个比arr[i]小的元素。设这个位置为L。这意味着从L+1到i的所有位置,arr[i]都是最小的。 -
右侧范围:类似地,我们找出在
arr[i]右侧的第一个比arr[i]小的元素。设这个位置为R。这意味着从i到R-1的所有位置,arr[i]都是最小的。
知道这两个位置后,我们可以计算以 arr[i] 为最小值的子数组数量。这个数量等于 arr[i] 左侧和右侧可扩展的位置数的乘积。
特别注意:处理数值相同时的情况。只需要在处理左边界或者有边界时候加入一个等号即可。(始终认为出现相同值时,右边的更小)。
代码
class Solution {
public:int sumSubarrayMins(vector<int>& arr) {stack<int> s;int result = 0;int n = arr.size();vector<int> left(n), right(n);long long mod = 1000000007; // 10^9 + 7for (int i = 0; i < n; ++i) {while (!s.empty() && arr[s.top()] >= arr[i]) {right[s.top()] = i;s.pop();}s.push(i);}while (!s.empty()) {right[s.top()] = n;s.pop();}for (int j = n-1; j >= 0; --j) {while (!s.empty() && arr[s.top()] > arr[j]) {left[s.top()] = j;s.pop();}s.push(j);}while (!s.empty()) {left[s.top()] = -1;s.pop();}for (int i = 0; i < n; ++i) {cout << i << " " << left[i] << " " << right[i] << " " << arr[i] << endl;result += ((long long)(i - left[i]) * (right[i] - i) % mod * arr[i] % mod) % mod;result %= mod;}return result;}
};特别感谢GPT的Code Tutor,这个题目的思路和代码是在它的指导下写出来的,还挺好用的。
时空复杂度

相关文章:

20240119-子数组最小值之和
题目要求 给定一个整数数组 arr,求 min(b) 的总和,其中 b 的范围涵盖 arr 的每个(连续)子数组。由于答案可能很大,因此返回答案模数 Example 1: Input: arr [3,1,2,4] Output: 17 Explanation: Subarrays are [3]…...

c# 释放所有嵌入资源, 到某个本地文件夹
版本号 .net 8 代码 using System.Reflection;namespace Demo;internal class Program {static void Main(string[] args){// 获取当前 执行exe 的目录 / 当前命令行所在的目录 var currentDir Directory.GetCurrentDirectory();Console.WriteLine(currentDir);Extract…...

Unity SnapScrollRect 滚动 匹配 列表 整页
展示效果 原理: 当停止滑动时 判断Contet的horizontalNormalizedPosition 与子Item的缓存值 相减,并得到最小值,然后将Content horizontalNormalizedPosition滚动过去 使用方式: 直接将脚本挂到ScrollRect上 注意:在创建Content子物体时…...

网络命令ping和telnet
1. 请解释ping和telnet的工作原理。 ping和telnet是两种常用的网络工具,其工作原理分别如下: ping: 目的:ping主要用于检查网络是否通畅以及测量网络连接速度。工作原理:ping是基于ICMP(Internet Control …...
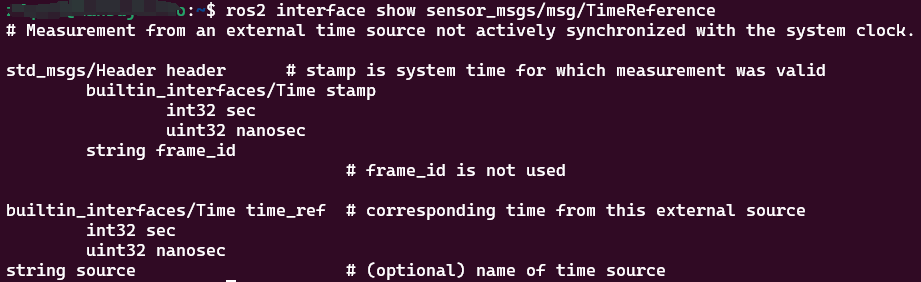
ros2学习笔记-CLI工具,记录命令对应操作。
目录 环境变量turtlesim和rqt以初始状态打开rqt node启动节点查看节点列表查看节点更多信息命令行参数 --ros-args topic话题列表话题类型话题列表,附加话题类型根据类型查找话题名查看话题发布的数据查看话题的详细信息查看类型的详细信息给话题发布消息࿰…...

自然语言处理的发展
自然语言处理的发展大致经历了四个阶段:萌芽期、快速发展期、低谷的发展期和复苏融合期。 萌芽期(1956年以前):这个阶段可以看作自然语言处理的基础研究阶段。人类文明经过了几千年的发展,积累了大量的数学、语言学和…...
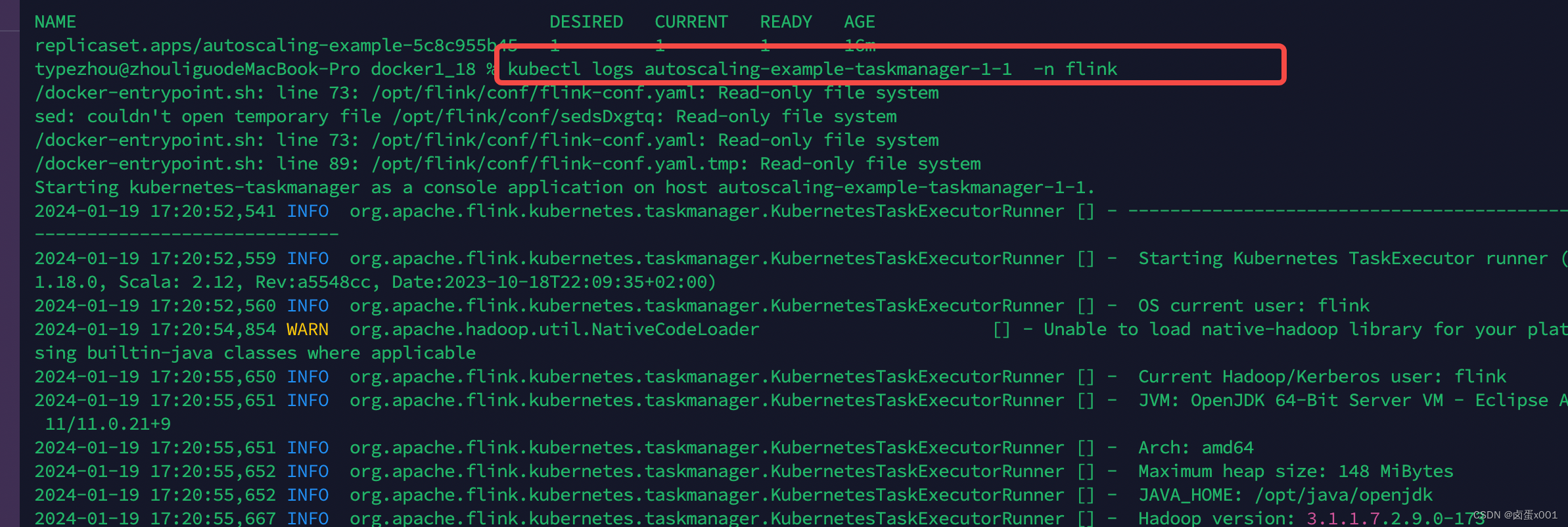
flink operator 拉取阿里云私有镜像(其他私有类似)
创建 k8s secret kubectl --namespace flink create secret docker-registry aliyun-docker-registry --docker-serverregistry.cn-shenzhen.aliyuncs.com --docker-usernameops_acr1060896234 --docker-passwordpasswd --docker-emailDOCKER_EMAIL注意命名空间指定你使用的 我…...

C语言算法赛——蓝桥杯(省赛试题)
一、十四届C/C程序设计C组试题 十四届程序C组试题A#include <stdio.h> int main() {long long sum 0;int n 20230408;int i 0;// 累加从1到n的所有整数for (i 1; i < n; i){sum i;}// 输出结果printf("%lld\n", sum);return 0; }//十四届程序C组试题B…...
【文本到上下文 #2】:NLP 的数据预处理步骤
一、说明 欢迎阅读此文,NLP 爱好者!当我们继续探索自然语言处理 (NLP) 的广阔前景时,我们已经在最初的博客中探讨了它的历史、应用和挑战。今天,我们更深入地探讨 NLP 的核心——数据预处理的复杂世界。 这篇文章是我们的“完整 N…...
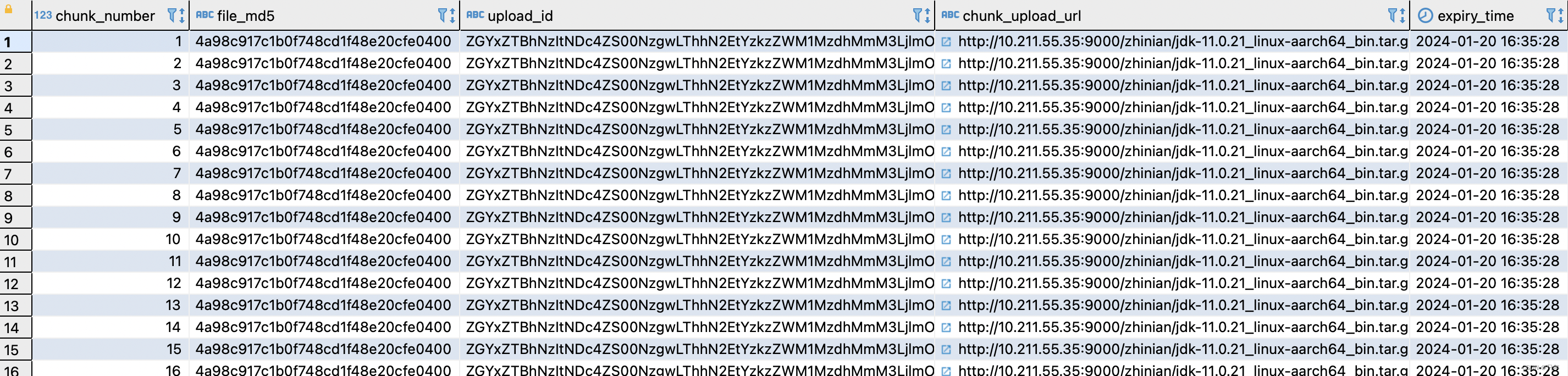
Minio文件分片上传实现
资源准备 MacM1Pro 安装Parallels19.1.0请参考 https://blog.csdn.net/qq_41594280/article/details/135420241 MacM1Pro Parallels安装CentOS7.9请参考 https://blog.csdn.net/qq_41594280/article/details/135420461 部署Minio和整合SpringBoot请参考 https://blog.csdn.net/…...
C语言总结十一:自定义类型:结构体、枚举、联合(共用体)
本篇博客详细介绍C语言最后的三种自定义类型,它们分别有着各自的特点和应用场景,重点在于理解这三种自定义类型的声明方式和使用,以及各自的特点,最后重点掌握该章节常考的考点,如:结构体内存对齐问题&…...

解决Spring Boot应用打包后文件访问问题
在Spring Boot项目的开发过程中,一个常见的挑战是如何有效地访问和操作资源文件。这一挑战尤其显著当应用从IDE环境(如IntelliJ IDEA)迁移到被打包成JAR文件后的生产环境。开发者经常遇到的问题是,在IDE中运行正常的代码ÿ…...

循环神经网络的变体模型-LSTM、GRU
一.LSTM(长短时记忆网络) 1.1基本介绍 长短时记忆网络(Long Short-Term Memory,LSTM)是一种深度学习模型,属于循环神经网络(Recurrent Neural Network,RNN)的一种变体。…...

视频图像的color range简介
介绍 研究FFmpeg发现,在avcodec.h中有关于color的解释,主要有四个属性,primaries、transfer、space和range。 color primaries: 基于RGB空间对应的绝对颜色XYZ的变换,决定了最终三原色RGB分别是什么颜色;…...

tcp的三次握手
http 和 https 都是是基于 TCP 的请求,https 是 http 加上 tls 连接。TCP 是面向连接的协议。 对于 http1.1 协议chrome 限制在同一个域名下最多可以建立 6 个 tcp 连接,所以如果在同一个域名下,同时有超过 6 个请求发生,那么多余…...

unity 矩阵探究
public void MatrixTest1(){ ///Matrix4x4 是列矩阵,就是一个vector4表示一列,所以在c#中矩阵和Vector4只能矩阵右乘坐标。但是在shader中是矩阵左乘坐标,所以在shader中是行矩阵 Matrix4x4 moveMatrix1 new Matrix4x4(new Vector4(1,0,0,0)…...
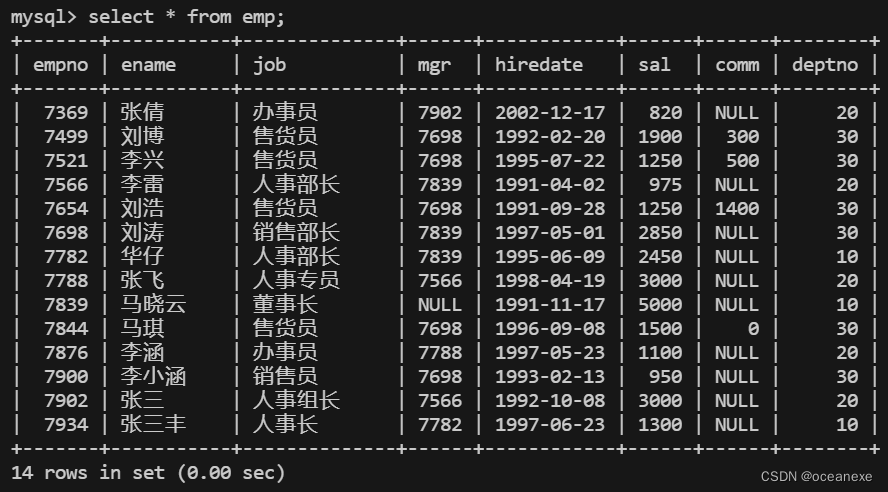
MySQL---单表查询综合练习
创建emp表 CREATE TABLE emp( empno INT(4) NOT NULL COMMENT 员工编号, ename VARCHAR(10) COMMENT 员工名字, job VARCHAR(10) COMMENT 职位, mgr INT(4) COMMENT 上司, hiredate DATE COMMENT 入职时间, sal INT(7) COMMENT 基本工资, comm INT(7) COMMENT 补贴, deptno INT…...

Python项目——搞怪小程序(PySide6+Pyinstaller)
1、介绍 使用python编写一个小程序,回答你是猪吗。 点击“是”提交,弹窗并退出。 点击“不是”提交,等待5秒,重新选择。 并且隐藏了关闭按钮。 2、实现 新建一个项目。 2.1、设计UI 使用Qt designer设计一个UI界面,…...

MySQL练习题
参考:https://blog.csdn.net/paul0127/article/details/82529216 数据表介绍 --1.学生表 Student(SId,Sname,Sage,Ssex) --SId 学生编号,Sname 学生姓名,Sage 出生年月,Ssex 学生性别 --2.课程表 Course(CId,Cname,TId) --CId 课程编号,Cname 课程名称,TId 教师编号…...

vue-项目打包、配置路由懒加载
1. 简介 在现代前端开发中,Vue.js因其简洁、灵活和高效的特点,已经成为许多开发者的首选框架。 在Vue项目中,打包部署和路由懒加载是两个非常重要的环节。 打包Vue项目是为了将源代码转换为浏览器可以解析的JavaScript文件,以便…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
