transformer和vit学习笔记
以下记录自己对transformer的学习笔记,可能自己看得懂【久了自己也忘了看不懂】,别人看起来有点乱。以后再优化文档~
小伙伴请直接去看学习资源:
Transformer的理解T-1_哔哩哔哩_bilibili
-
首先,时序处理:一些模型的出现。
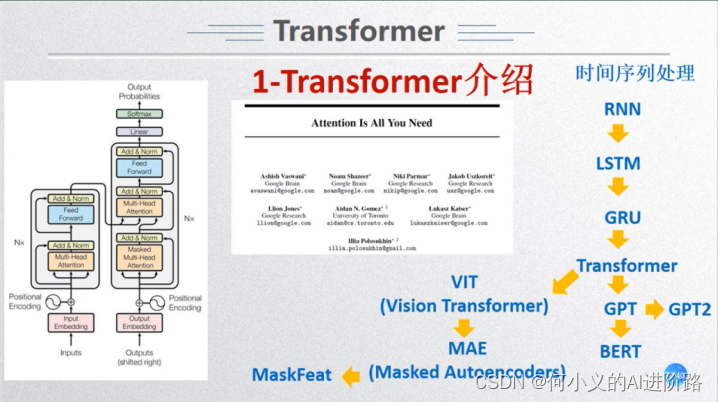
NLP方面继续:
GPT2 -> GPT3 -> GPT4, chatGPT
图像方面:
分类:VIT , Swin Transformer, TNT(TRM in TRM)
检测:DERT等基于trm的目标检测模型;
分割:VisTR等基于trm的图像分割模型(A Survey of Visual Transformers)
预训练模型进阶【大一统,CV大模型初步】:MAE -> SAM(segment anything)
- Transformer
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30. ( 谷歌 NIPS 2017)
Transformer改进了RNN最被人诟病的训练慢的缺点,利用self-attention机制实现快速并行。并且Transformer可以增加到非常深的深度,充分发掘DNN模型的特性,但是模型本身很简洁,提升模型准确率。

- Inputs:比如一句话,四个词语!
- Input Embedding: 四个词语,每个embedding成512维! X:4*512 [x1,x2,x3,x4] 分别:1*512
- Positional Encoding: 位置编码 【一句话中每个词之间有一种相对位置,同一个词不同位置,让每一个位置都有不同的编码,才更有意义 最终用:Final Embedding.】


pos:第几个位置,i:第几个编码维度,d-model:同embedding一致的总维度,如512
奇数维度sin,偶数维度cos 【公式:第几个位置的第几维度,得到一个position值】

纵坐标:位置, 横坐标:维度
对于Multi-Head Attention:


Q(query),K(key),V(value): 每一个词语的每一个q k v都是1*512 来源:
q1 = x1*Wq = [1 512] * [512 512] = [1 512] k1和v1同理!【第2-4个词同理】
QKT = [4 512]*[512 4] = [4 4] 根号dk为常熟,负责缩减值。
*V = [4 4] * [4*512] = [4 512] 因此,最终self-attation值还是4*512 = X:4*512


值得一提的是当有多个句子,每个句子有不同的数量的词语,计算中矩阵需要进行补充掩码!
比如5个有的只有3个。不够的全都掩码到5个!

有的是Q-padding, 有的是K-padding 【常用】 三个句子3个词4个词5个词最终都是5*512!
对于多头注意力的体现?
假如Q K V 4*512 分层成4*256与 4*256 【图中是三份,这里两份】
每个4*256分别计算自己的四个样本词的自注意力,最后它们再concat合并起来!


对于:Masked Multi-head attention
不同于encoder中,对输入数据X的自注意力计算,decoder中是需要逐个预测output的输出的,因此第一次保留第一个词语开始符<sos>,掩盖住后面的,第二次保留前两个词语,掩盖住后边的,知道最后得到结束符<eos>,预测结束。

这里的mask方式是对V构造上三角掩盖:
补充句子长度一致q-padding或者k-padding,掩掉句子长度
这里decoder是每次预测结果掩盖后边句子,是把QKT掩盖构造的上三角矩阵,再乘V!

对于结构中剩余模块:多头注意力后的短接,归一化,前馈神经网络,最后线性层+softmax等等。最终输出Output Probability比如:4*C的矩阵,C是类别数量。
Visual Transformer
Dosovitskiy A , Beyer L , Kolesnikov A ,et al.An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale[C]//International Conference on Learning Representations.2021. (谷歌)
问题:transformer 从NLP到 CV???


复杂度高,且每个像素值作为一个token并不合理!!!
>>> 思路:
图片分块固定大小,线性嵌入特征+位置编码特征,喂给TRM的encoder~
增加可扩展的分类token


优点:有局部,合起来也有全局!
vit中TRM与TRM原论文有点结构上的变化:norm提前了,而且没有PAD掩码【猜测是样本图resize统一,分割出来的token是一样的】
具体的如下步骤:


一些VIT的细节解释:
首先,输出特征怎么利用:
一般可以两种⽅式,⼀种是使⽤【CLS】token,另⼀种就是对所有tokens的输出做⼀个平均
最后选择加一个分类用的token-0:因为计算中也会和每一个算自注意力【不用每个token的高阶encoder输出再合并特征接全连接层了,用token0的也行,隐藏着特征带有全图全局信息了的了】

一些计算过程:

P:图片块分辨率,H*W/P*P = N数量,图分成了N块 【要看论文,一开始博主讲的P2块】
C:每块图通道,比如3,
D:维度,比如 512 【代码中:一块图P*P*3->conv+fc->D维embedding】
E:输入特征【N*D】比如 N=9块,这里9*512 Epos:位置编码特征,维度保持一致D!【这里是10*512】
Z0:VIT里边的patch+position的综合embedding了【加Xclass的token-0】
MSA:多头注意力,LN:norm 加后边的Zl-1:残差机制
MLP一行同理1 以上在图中也可以loop循环堆叠。
相关文章:

transformer和vit学习笔记
以下记录自己对transformer的学习笔记,可能自己看得懂【久了自己也忘了看不懂】,别人看起来有点乱。以后再优化文档~ 小伙伴请直接去看学习资源: Transformer的理解T-1_哔哩哔哩_bilibili 首先,时序处理:一些模型的出…...
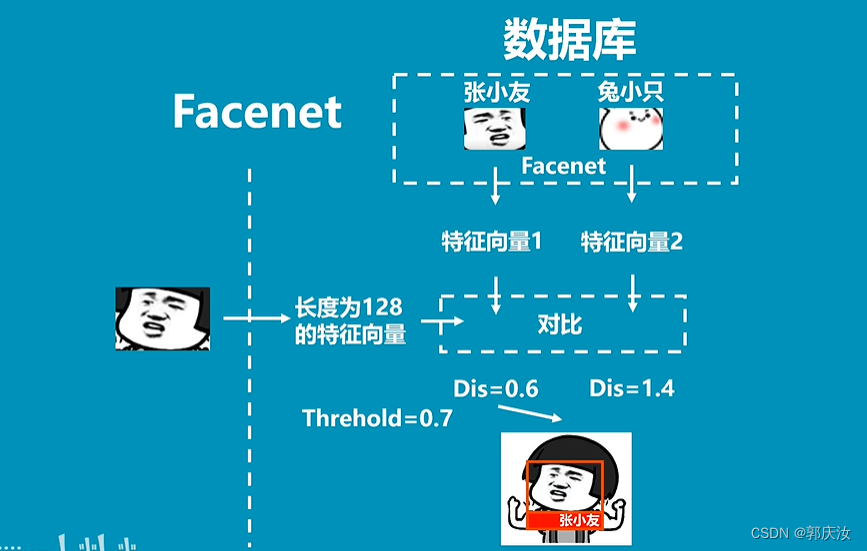
人脸识别 FaceNet人脸识别(一种人脸识别与聚类的统一嵌入表示)
人脸识别 FaceNet人脸识别(一种人脸识别与聚类的统一嵌入表示) FaceNet的简介Facenet的实现思路训练部分 FaceNet的简介 Facenet的实现思路 import torch.nn as nndef conv_bn(inp, oup, stride 1):return nn.Sequential(nn.Conv2d(inp, oup, 3, stride…...

Python tkinter (6) Listbox
Python的标准Tk GUI工具包的接口 tkinter系列文章 python tkinter窗口简单实现 Python tkinter (1) —— Label标签 Python tkinter (2) —— Button标签 Python tkinter (3) —— Entry标签 Python tkinter (4) —— Text控件 GUI 目录 Listbox 创建listbox 添加元素…...
优雅的python(二)
🌈个人主页:小田爱学编程 🔥 系列专栏:c语言从基础到进阶 🏆🏆关注博主,随时获取更多关于c语言的优质内容!🏆🏆 😀欢迎来到小田代码世界~ &#x…...
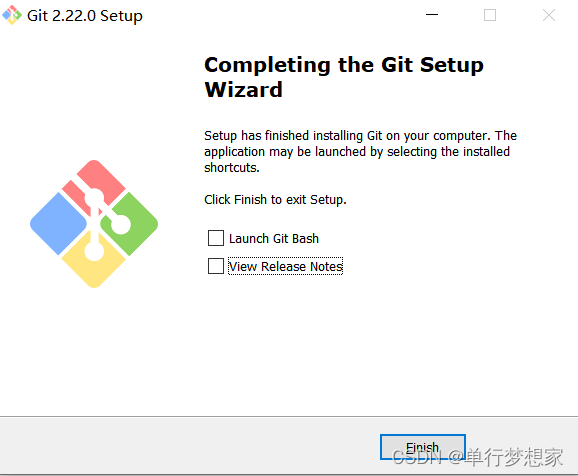
Git安装详细步骤
目录 1、双击安装包,点击NEXT编辑 2、更改安装路径,点击NEXT 3、选择安装组件 4、选择开始菜单页 5、选择Git文件默认的编辑器 6、调整PATH环境 7、选择HTTPS后端传输 8、配置行尾符号转换 9、配置终端模拟器与Git Bash一起使用 10、配置额外…...

首发:2024全球DAO组织发展研究
作者,张群(专注DAO及区块链应用研究,赛联区块链教育首席讲师,工信部赛迪特邀资深专家,CSDN认证业界专家,微软认证专家,多家企业区块链产品顾问) DAO(去中心化自治组织&am…...

【大数据】详解 Flink 中的 WaterMark
详解 Flink 中的 WaterMark 1.基础概念1.1 流处理1.2 乱序1.3 窗口及其生命周期1.4 Keyed vs Non-Keyed1.5 Flink 中的时间 2.Watermark2.1 案例一2.2 案例二2.3 如何设置最大乱序时间2.4 延迟数据重定向 3.在 DDL 中的定义3.1 事件时间3.2 处理时间 1.基础概念 1.1 流处理 流…...
【数据结构1-2】二叉树
树形结构不仅能表示数据间的指向关系,还能表示出数据的层次关系,而有很明显的递归性质。因此,我们可以利用树的性质解决更多种类的问题。 但是在平常的使用中,我们并不需要使用这么复杂的结构,只需要建立一个包含int r…...
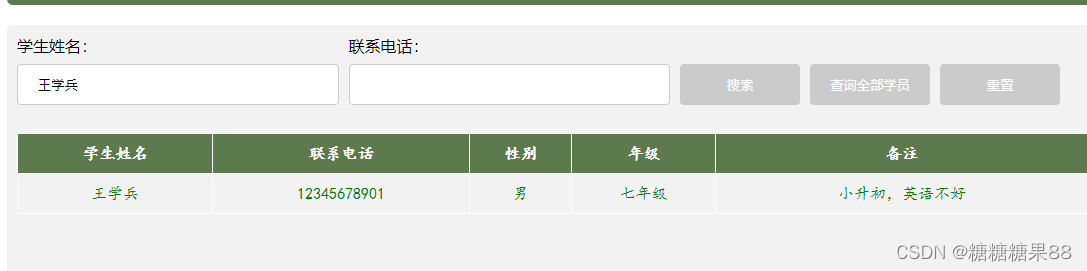
ajax点击搜索返回所需数据
html 中body设置(css设置跟进自身需求) <p idsearch_head>学生信息查询表</p> <div id"div_1"> <div class"search_div"> <div class"search_div_item"> …...

Redis6基础知识梳理~
初识NOSQL: NOSQL是为了解决性能问题而产生的技术,在最初,我们都是使用单体服务器架构,如下所示: 随着用户访问量大幅度提升,同时产生了大量的用户数据,单体服务器架构面对着巨大的压力 NOSQL解…...

在Python中如何使用集合进行元素操作
目录 1. 创建集合 2. 添加或删除元素 3. 集合运算 4. 其他集合操作 总结 在Python中,集合(set)是一种基本的数据结构,用于存储无序且唯一的元素。这意味着集合中的每个元素都是独一无二的,且集合不保持任何元素的…...
2024年阿里云幻兽帕鲁Palworld游戏服务器优惠价格表
自建幻兽帕鲁服务器租用价格表,2024阿里云推出专属幻兽帕鲁Palworld游戏优惠服务器,配置分为4核16G和4核32G服务器,4核16G配置32.25元/1个月、10M带宽66.30元/1个月、4核32G配置113.24元/1个月,4核32G配置3个月339.72元。ECS云服务…...
)
Atlassian Confluence Data Center and Server 权限提升漏洞复现(CVE-2023-22515)
0x01 产品简介 Atlassian Confluence是一款由Atlassian开发的企业团队协作和知识管理软件,提供了一个集中化的平台,用于创建、组织和共享团队的文档、知识库、项目计划和协作内容。是面向大型企业和组织的高可用性、可扩展性和高性能版本。 0x02 漏洞概述 Atlassian Confl…...
打开 IOS开发者模式
前言 需要 1、辅助设备:苹果电脑; 2、辅助应用:Xcode; 3、准备工作:苹果手机 使用数据线连接 苹果电脑; 当前系统版本 IOS 17.3 通过Xcode激活 两指同时点击 Xcode 显示选择,Open Develop…...

【C语言刷题系列】交换两个变量的三种方式
文章目录 1.使用临时变量(推荐) 2.相加和相减的方式(值较大时可能丢失数据) 3.按位异或运算 本文所属专栏C语言刷题_倔强的石头106的博客-CSDN博客 两个变量值的交换是编程中最常见的问题之一,以下将介绍三种变量的…...
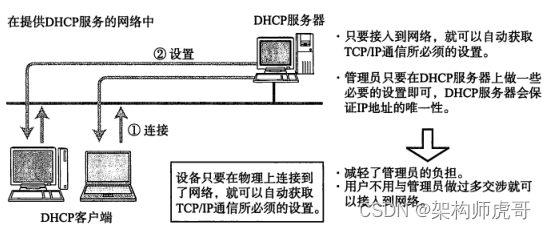
架构师之路(十五)计算机网络(网络层协议)
前置知识(了解):计算机基础。 作为架构师,我们所设计的系统很少为单机系统,因此有必要了解计算机和计算机之间是怎么联系的。局域网的集群和混合云的网络有啥区别。系统交互的时候网络会存在什么瓶颈。 ARP协议 地址解…...
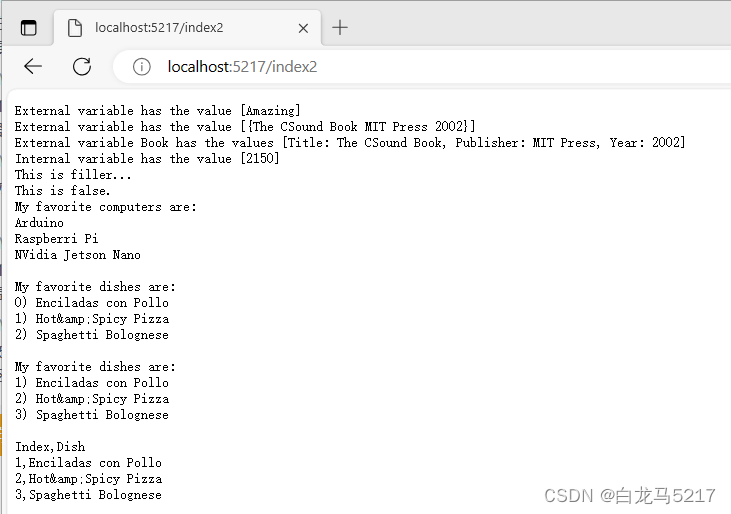
【JSON2WEB】03 go的模板包html/template的使用
Go text/template 是 Go 语言标准库中的一个模板引擎,用于生成文本输出。它使用类似于 HTML 的模板语言,可以将数据和模板结合起来,生成最终的文本输出。 Go html/template包实现了数据驱动的模板,用于生成可防止代码注入的安全的…...
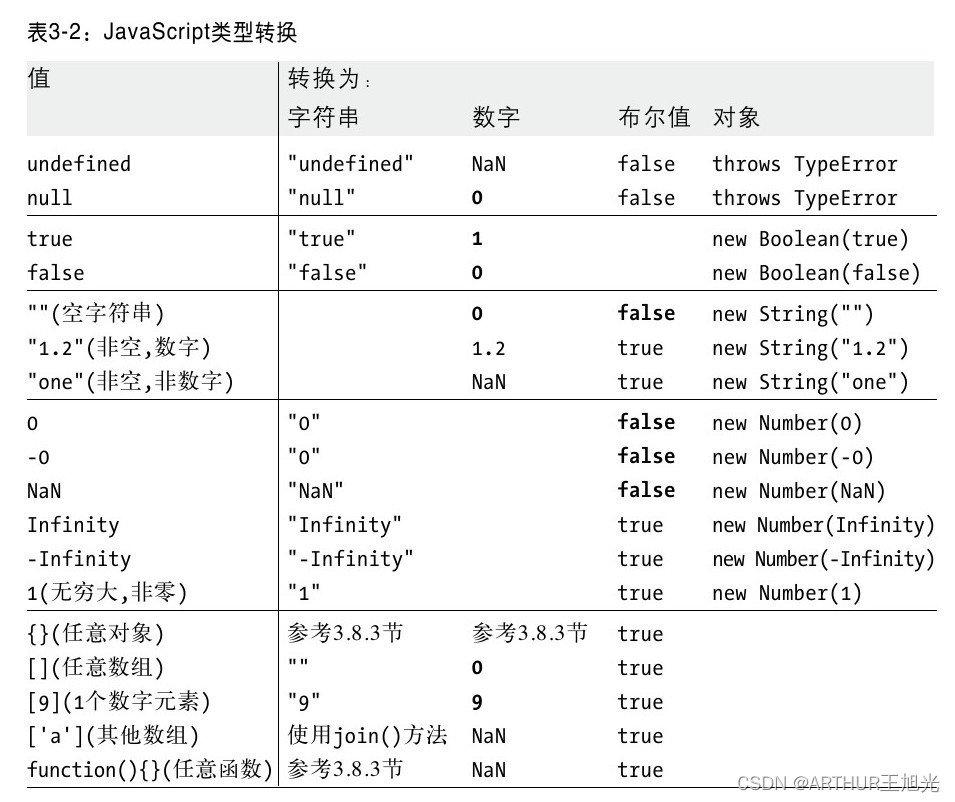
3 JS类型 值和变量
计算机对value进行操作。 value有不同的类型。每种语言都有其自身的类型集合。编程语言的类型集是该编程语言的基本特性。 value需要保存一个变量中。 变量的工作机制是变成语言的另一个基本特性。 3.1概述和定义 JS类型分为: 原始类型和对象类型。 原始类型&am…...

【Android】实现简易购物车功能(附源码)
先上结果: 代码: 首先引入图片加载: implementation com.github.bumptech.glide:glide:4.15.1配置权限清单: <!-- 网络权限 --><uses-permission android:name"android.permission.INTERNET"/><uses…...

使用Excel计算--任务完成总工作日时间段
(Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 引言 计算任务完成时间周期,和计算金钱一样,是一个比较细致严谨的工作。 通常,我们可能以为,完成周期形如: 任务完成周期 任务结束时间 - 任务开始时间 但是…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
