每日一题 力扣2846 边权重均等查询
2846. 边权重均等查询
题目描述:
现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。
另给你一个长度为 m 的二维整数数组 queries ,其中 queries[i] = [ai, bi] 。对于每条查询,请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。
注意:
- 查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
- 从
ai到bi的路径是一个由 不同 节点组成的序列,从节点ai开始,到节点bi结束,且序列中相邻的两个节点在树中共享一条边。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 条查询的答案。
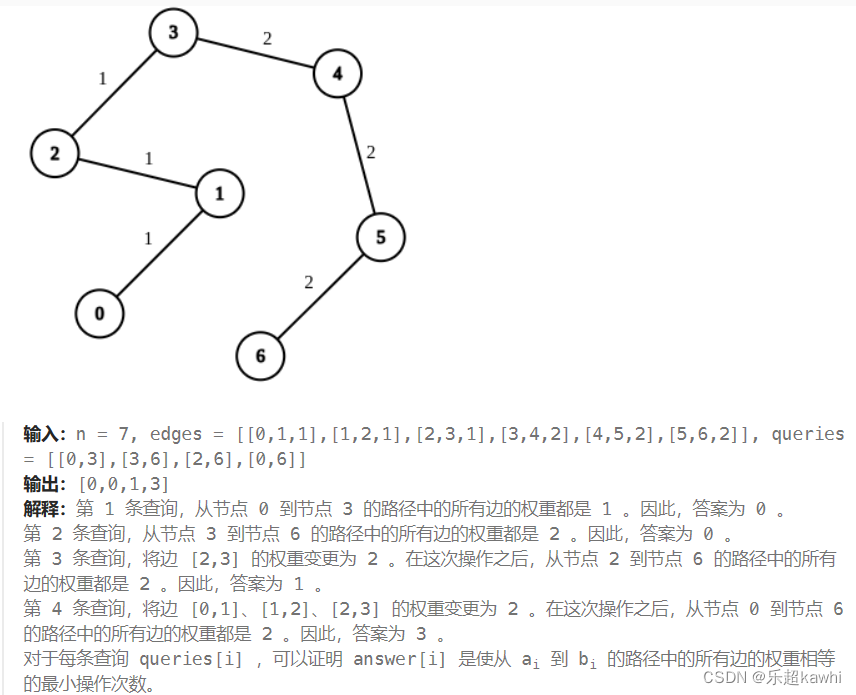
示例1:
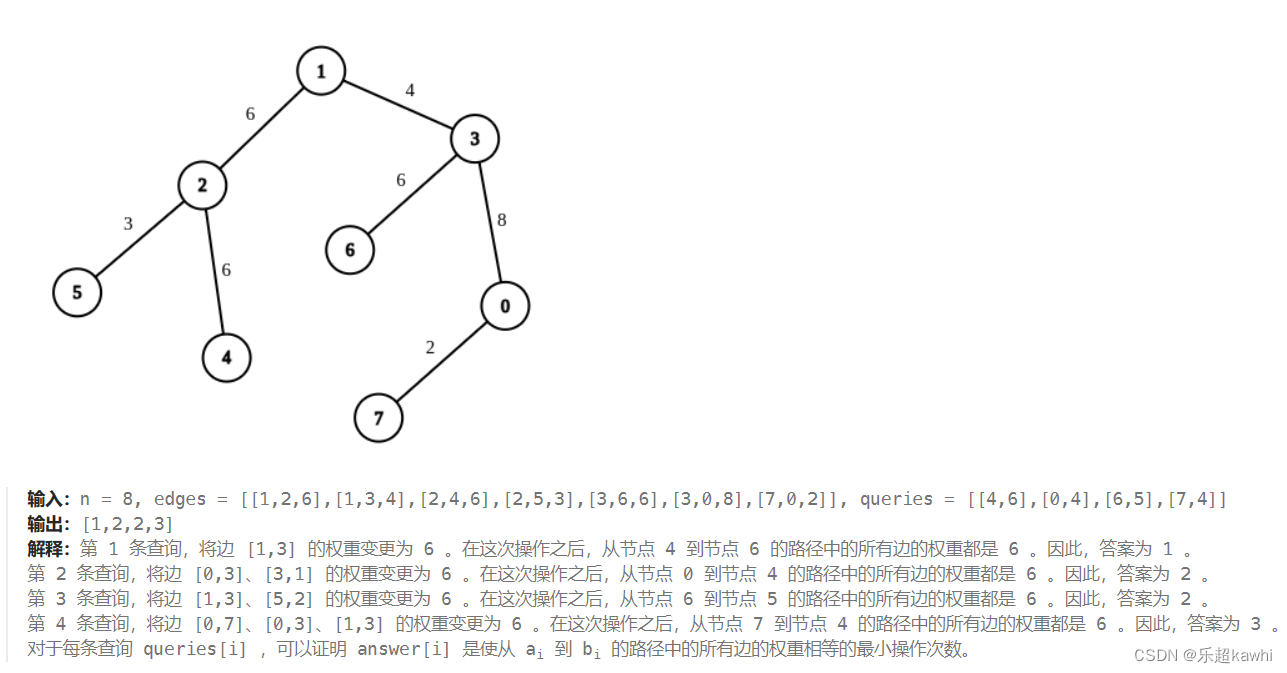
示例2:
提示:
1 <= n <= 10^4edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= wi <= 26- 生成的输入满足
edges表示一棵有效的树1 <= queries.length == m <= 2 * 104queries[i].length == 20 <= ai, bi < n
思路:
要我们以queries数组为遍历基础,先找到ai到bi的路径,然后统计路径上的权值,找到频次最高的权值出现的次数,用路径长度-频次即为所求的最小操作次数。
求最近公共祖先,LCA(Least Common Ancestors),即最近公共祖先,这种描述是基于树结构的,也即我们通通常只在树结构中考虑祖先问题。树实际上就是图论中的有向无环图,而要研究LCA问题,首先我们要指定树中的一个顶点为根节点,并以该节点遍历有向无环图,生成一颗DFS序下的树,假设我们要查询的两个节点为u,v,DFS序下根节点到两点的最短路径分别是(r,u),和(r,v),LCA就是(r,u)与(r,v)公共路径的最后一个节点。
而求两点间的路径长度,可以通过倍增法求 LCA 来实现。我们记两点分别为 u 和 v,最近公共祖先为 x,那么 u 到 v的路径长度就是 depth(u)+depth(v)−2×depth(x)。
另外,我们可以用一个数组 cnt[n][26] 记录根节点到每个节点上,每个边权重出现的次数。那么 u 到 v 的路径上,出现次数最多的边的次数就是 max0≤j<26cnt[u][j]+cnt[v][j]−2×cnt[x][j]。其中 x 为 u和 v的最近公共祖先。

代码:
class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {int m = 32 - __builtin_clz(n);vector<pair<int, int>> g[n];int f[n][m];int p[n];int cnt[n][26];int depth[n];memset(f, 0, sizeof(f));memset(cnt, 0, sizeof(cnt));memset(depth, 0, sizeof(depth));memset(p, 0, sizeof(p));for (auto& e : edges) {int u = e[0], v = e[1], w = e[2] - 1;g[u].emplace_back(v, w);g[v].emplace_back(u, w);}queue<int> q;q.push(0);while (!q.empty()) {int i = q.front();q.pop();f[i][0] = p[i];for (int j = 1; j < m; ++j) {f[i][j] = f[f[i][j - 1]][j - 1];}for (auto& [j, w] : g[i]) {if (j != p[i]) {p[j] = i;memcpy(cnt[j], cnt[i], sizeof(cnt[i]));cnt[j][w]++;depth[j] = depth[i] + 1;q.push(j);}}}vector<int> ans;for (auto& qq : queries) {int u = qq[0], v = qq[1];int x = u, y = v;if (depth[x] < depth[y]) {swap(x, y);}for (int j = m - 1; ~j; --j) {if (depth[x] - depth[y] >= (1 << j)) {x = f[x][j];}}for (int j = m - 1; ~j; --j) {if (f[x][j] != f[y][j]) {x = f[x][j];y = f[y][j];}}if (x != y) {x = p[x];}int mx = 0;for (int j = 0; j < 26; ++j) {mx = max(mx, cnt[u][j] + cnt[v][j] - 2 * cnt[x][j]);}ans.push_back(depth[u] + depth[v] - 2 * depth[x] - mx);}return ans;}
};大意我懂了,但是俺似乎写不出来这么完整的,哭!然后继续学!
相关文章:

每日一题 力扣2846 边权重均等查询
2846. 边权重均等查询 题目描述: 现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重…...

【Docker】Docker学习⑨ - 单机编排之Docker Compose
【Docker】Docker学习⑨ - 单机编排之Docker Compose 一、Docker简介二、Docker安装及基础命令介绍三、Docker镜像管理四、Docker镜像与制作五、Docker数据管理六、网络部分七、Docker仓库之单机Dokcer Registry八、Docker仓库之分布式Harbor九、单机编排之Docker Compose1 基础…...

ES6笔记-symbol
ES6 symbol 是什么 ES5的对象属性名是字符串,这容易造成属性名的冲突。symbol是一种机制,保证每个属性的名字都是独一无二的。这样就从根本上防止属性名冲突。 它是一种原始数据类型Symbol,表示独一无二的值。它属于javaScript语言的原生数据类型之一。…...

C++设计模式介绍:优雅编程的艺术
物以类聚 人以群分 文章目录 简介为什么有设计模式? 设计模式七大原则单一职责原则(Single Responsibility Principle - SRP)开放封闭原则(Open/Closed Principle - OCP)里氏替换原则(Liskov Substitution …...

GitLab升级版本(任意用户密码重置漏洞CVE-2023-7028)
目录 前言漏洞分析影响范围查看自己的GitLab版本升级路程 升级过程13.1.1113.8.8 - 14.0.1214.3.614.9.5 - 16.1.6 前言 最近GitLab发了个紧急漏洞需要修复,ok接到命令立刻着手开始修复,在修复之前先大概了解一下这个漏洞是什么东西 漏洞分析 1、组件…...
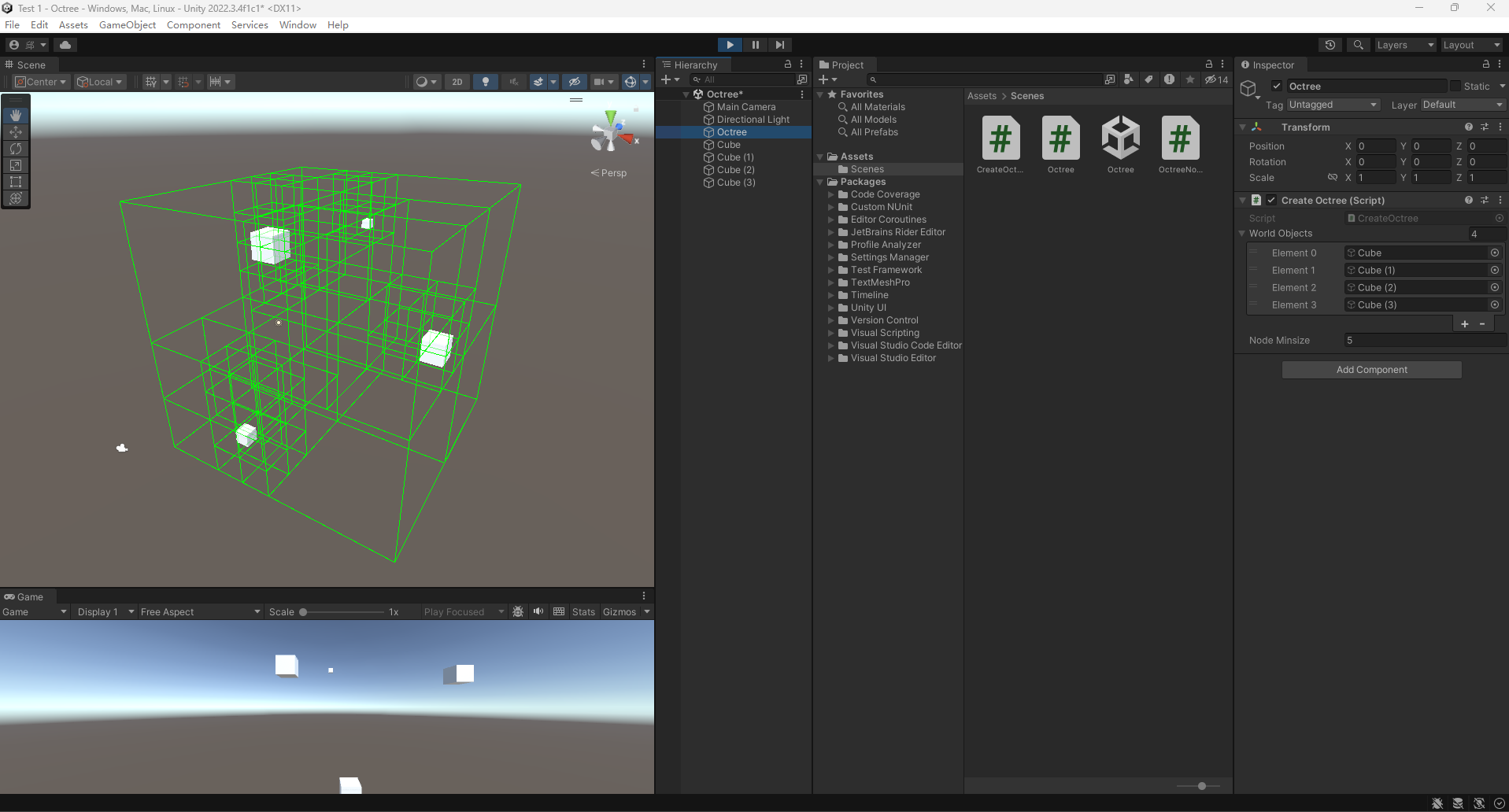
Unity——八叉树的原理与实现
八叉树原理 八叉树(Octree)是一种用于在三维空间中进行空间分割的数据结构。它将三维空间递归地划分为八个子空间,每个子空间对应于一个八叉树节点。这种分割方式可以有效地组织和管理场景中的对象,提高检索效率,特别…...

android 自定义软键盘的显示和隐藏
记一下,以后不用找在InputMethodService中有这两个方法可以看到软键盘显示状态 //软键盘隐藏 override fun onWindowHidden() {super.onWindowHidden() } //软键盘显示 override fun onWindowShown() {super.onWindowShown() } 在activity中可以通过这种方法看到软键盘显示状…...
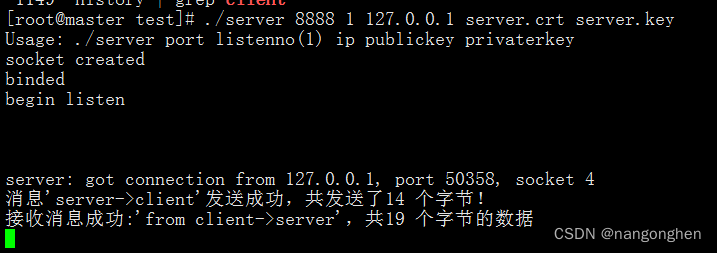
基于openssl v3搭建ssl安全加固的c++ tcpserver
1 概述 tcp server和tcp client同时使用openssl库,可对通信双方流通的字节序列进行加解密,保障通信的安全。本文以c编写的tcp server和tcp client为例子,openssl的版本为v3。 2 安装openssl v3 2.1 安装 perl-IPC-Cmd openssl项目中的co…...
)
11.2 Web开发_CSS入门(❤❤)
11.2 Web开发_CSS入门❤❤ 1. CSS简介1.1 基础案例2. CSS书写的位置2.1 行内式2.2 内嵌式2.3 外链式3. CSS基础选择器3.1 标签选择器3.2 id选择器3.3 类选择器3.4 选择器优先级3.5 通配符选择器4. 多类名5. 样式的两种特性5.1 层叠性...
[docker] Docker的数据卷、数据卷容器,容器互联
一、数据卷(容器与宿主机之间数据共享) 数据卷是一个供容器使用的特殊目录,位于容器中。可将宿主机的目录挂载到数据卷上,对数据卷的修改操作立刻可见,并且更新数据不会影响镜像,从而实现数据在宿主机与容…...
ATF(TF-A)安全通告TF-V11——恶意的SDEI SMC可能导致越界内存读取(CVE-2023-49100)
目录 一、ATF(TF-A)安全通告TFV-11 (CVE-2023-49100) 二、透过事务看本质SDEI是干啥的呢? 三、CVE-2023-49100 1、GICv2 systems 2、GICv3 systems 四、漏洞修复 一、ATF(TF-A)安全通告TFV-11 (CVE-2023-49100) Title 恶意的SDEI SMC可能导致越界内存读取&am…...
如何查找SpringBoot应用中的请求路径(不使用idea)
背景 昨天有个同事向我咨询某个接口的物理表是哪个,由于公司业务较多、这块业务的确不是我负责的,也没有使用idea不能全局搜索(eclipse搜不到jar内的字符串),也就回复了不清楚。 除了自己写代码输出servlet的路径和类外,发现了一…...
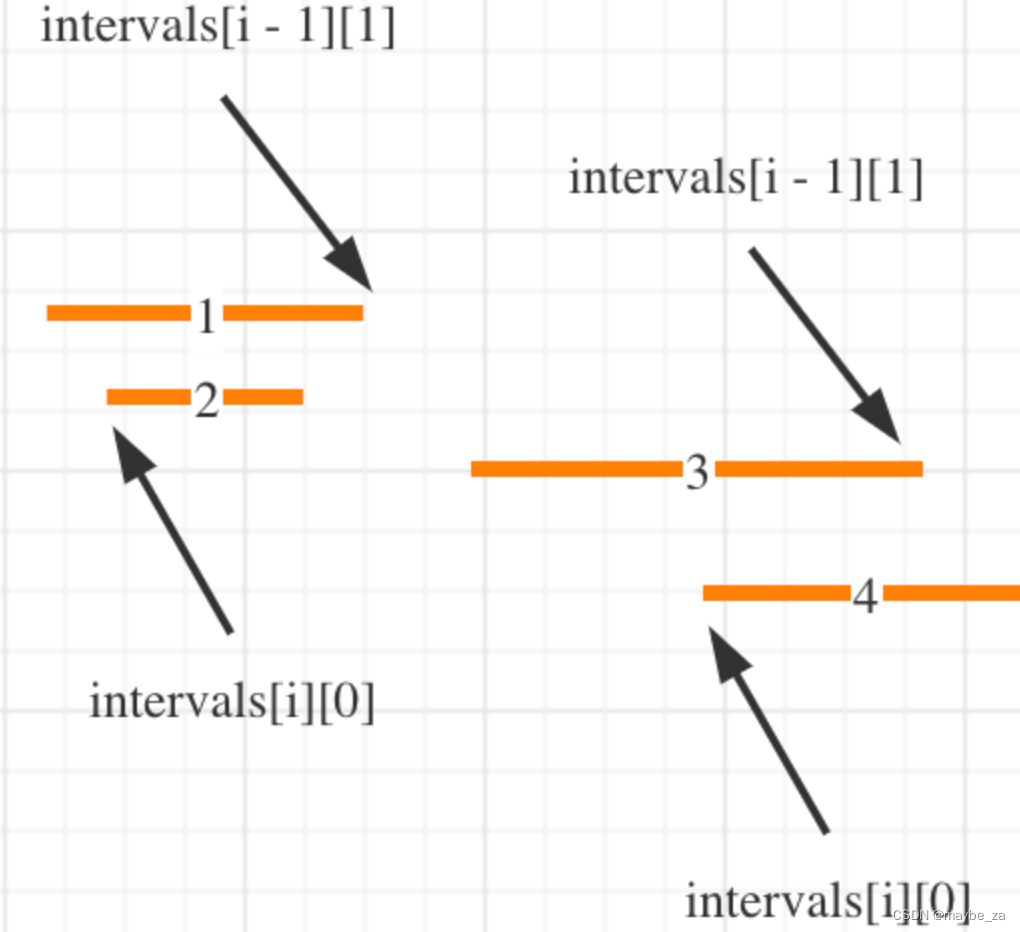
56. 合并区间 - 力扣(LeetCode)
题目描述 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 题目示例 输入:intervals [[1,3…...

数据结构篇-03:堆实现优先级队列
本文着重在于讲解用 “堆实现优先级队列” 以及优先级队列的应用,在本文所举的例子中,可能使用优先级队列来解并不是最优解法,但是正如我所说的:本文着重在于讲解“堆实现优先级队列” 堆实现优先级队列 堆的主要应用有两个&…...
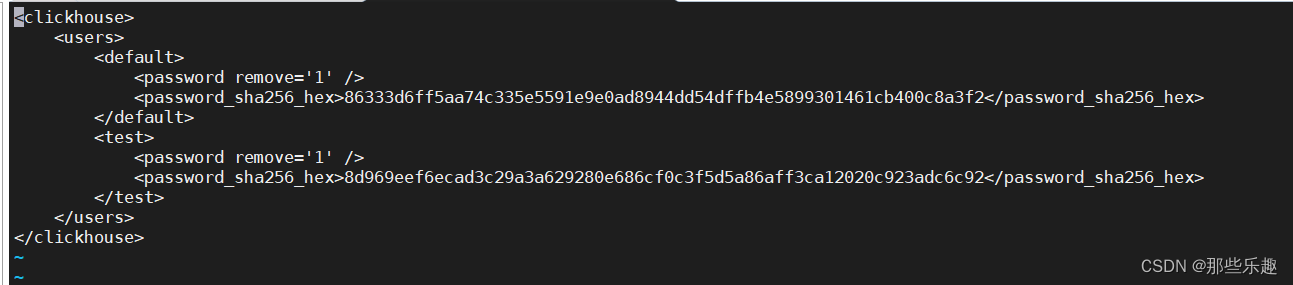
linux clickhouse 安装
1、官网下载clickhouse安装包 下载地址, clickhouse分lts和stable版本,lts是长期版本,一般选择安装lts版本。 其中clickhouse-server是clickhouse服务,就是用来访问数据存储数据,clickhouse-client是用来通过命令访问数…...

【游戏客户端开发的进阶路线】
*** 游戏客户端开发的进阶路线 春招的脚步越来越近,我们注意到越来越多的同学们都在积极学习游戏开发,希望能在这个充满活力的行业中大展拳脚。 当我们思考如何成为游戏开发领域的佼佼者时,关键在于如何有效规划学习路径。 🤔 我…...
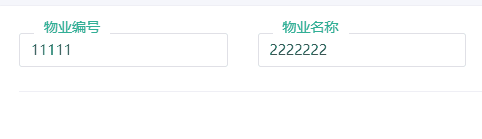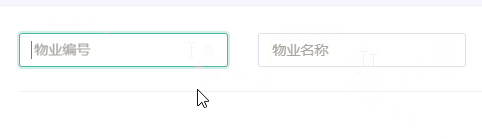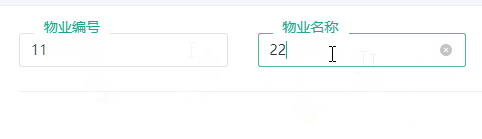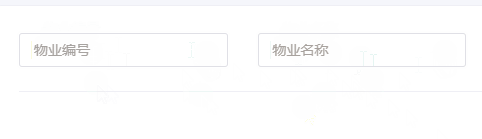
vue3+naiveUI二次封装的v-model 联动输入框
根据官网说明使用 源码 <template><div class"clw-input pt-3"><n-inputref"input":value"modelValue":type"type":title"title"clearable:disabled"disabled":size"size"placeholder&…...
百度Apollo | 实车自动驾驶:感知、决策、执行的无缝融合
🎬 鸽芷咕:个人主页 🔥 个人专栏:《linux深造日志》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下…...

DAY31:贪心算法入门455、53、376
理论基础 贪心算法的基本思路是通过局部最优从而达到全局最优,但是有时候局部最优并不一定导致全局最优,这样就需要动态规划的方法。但一部分题目是能通过贪心得到的。贪心的证明一般用到数学归纳法和反证法。在实际的问题中,没有统一的代码…...

LeetCode:376.摆动序列
个人主页:仍有未知等待探索-CSDN博客 专题分栏:算法_仍有未知等待探索的博客-CSDN博客 题目链接:376. 摆动序列 - 力扣(LeetCode) 一、题目 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...