DAY31:贪心算法入门455、53、376
理论基础
贪心算法的基本思路是通过局部最优从而达到全局最优,但是有时候局部最优并不一定导致全局最优,这样就需要动态规划的方法。但一部分题目是能通过贪心得到的。贪心的证明一般用到数学归纳法和反证法。在实际的问题中,没有统一的代码套路和模板,具体问题具体分析。
Leetcode: 455 分发饼干
一种思路是先把小饼干给小胃口的人
时间复杂度:O(nlogn)
空间复杂度:O(1)
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int index = 0;sort(g.begin(), g.end());//注意需要先排序sort(s.begin(), s.end());for(int i = 0; i < s.size(); i++){//饼干的个数if(index < g.size() && g[index] <= s[i]){//从最小的胃口开始index++;}}return index;}
};另一种思路是把大饼干先给大胃口的人
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int result = 0;int index = s.size() - 1;sort(g.begin(), g.end());sort(s.begin(), s.end());for(int i = g.size() - 1; i >= 0; i--){//胃口if(index >= 0 && g[i] <= s[index]){result++;index--;}}return result;}
};Leetcode: 53 最大子序和
贪心的思路是,设计一个count,当连续和为负数的时候,加上后面的数字就会变小,因此只要连续和不为负数就可以继续往下贪心。
时间复杂度:O(n)
空间复杂度:O(1)
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN;int count = 0;for(int i = 0; i < nums.size(); i++){count += nums[i];//计算count,元素和if(count > result) result = count;if(count <= 0) count = 0;//如果为负数了,就重新更新}return result;}
};可以看到贪心算法的代码还算简单,但是思路并不是很好想到。
Leetcode: 376 摆动序列
这道题思路太复杂了,但是代码很简单,这次先学习思路,之后还需要继续刷题
代码随想录
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff}}return result;}
};相关文章:

DAY31:贪心算法入门455、53、376
理论基础 贪心算法的基本思路是通过局部最优从而达到全局最优,但是有时候局部最优并不一定导致全局最优,这样就需要动态规划的方法。但一部分题目是能通过贪心得到的。贪心的证明一般用到数学归纳法和反证法。在实际的问题中,没有统一的代码…...

LeetCode:376.摆动序列
个人主页:仍有未知等待探索-CSDN博客 专题分栏:算法_仍有未知等待探索的博客-CSDN博客 题目链接:376. 摆动序列 - 力扣(LeetCode) 一、题目 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称…...
Stable Diffusion插件Recolor实现黑白照片上色
今天跟大家分享一个使用Recolor插件通过SD实现老旧照片轻松变彩色,Recolor翻译过来的含义就是重上色,该模型可以保持图片的构图,它只会负责上色,图片不会发生任何变化。 一:插件下载地址 https://github.com/pkuliyi…...

Android 音频焦点管理
前言 前面写过一篇类似的文章,没写完,今天再详细描述一下。 Android音频焦点申请处理 音频焦点管理的意义 两个或两个以上的 Android 应用可同时向同一输出流播放音频。系统会将所有音频流混合在一起。虽然这是一项出色的技术,但却会给用…...
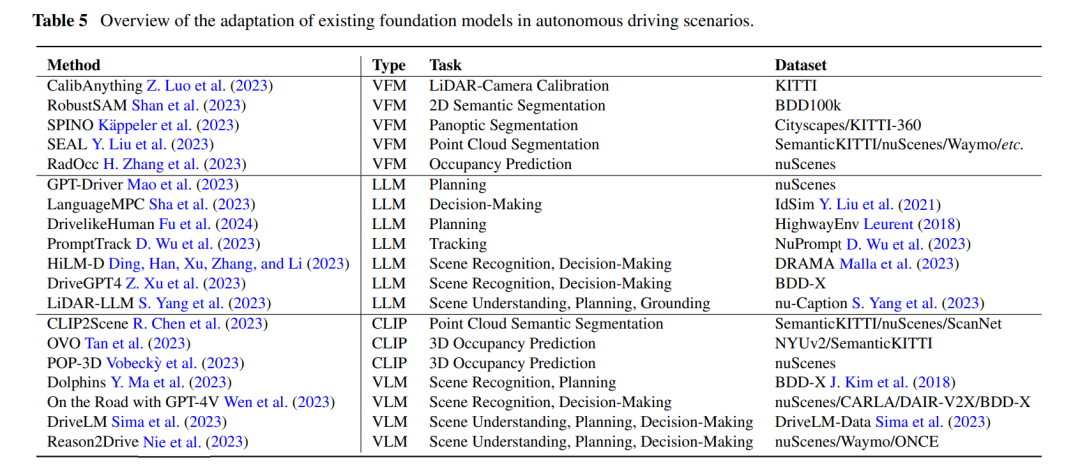
大模型+自动驾驶
论文:https://arxiv.org/pdf/2401.08045.pdf 大型基础模型的兴起,它们基于广泛的数据集进行训练,正在彻底改变人工智能领域的面貌。例如SAM、DALL-E2和GPT-4这样的模型通过提取复杂的模式,并在不同任务中有效地执行,从…...
openssl3.2 - 测试程序的学习 - test\aesgcmtest.c
文章目录 openssl3.2 - 测试程序的学习 - test\aesgcmtest.c概述笔记能学到的流程性内容END openssl3.2 - 测试程序的学习 - test\aesgcmtest.c 概述 openssl3.2 - 测试程序的学习 aesgcmtest.c 工程搭建时, 发现没有提供 test_get_options(), cleanup_tests(), 需要自己补上…...

C语言——操作符详解2
目录 0.过渡0.1 不创建临时变量,交换两数0.2 求整数转成二进制后1的总数 1.单目表达式2. 逗号表达式3. 下标访问[ ]、函数调用( )3.1 下标访问[ ]3.2 函数调用( ) 4. 结构体成员访问操作符4.1 结构体4.1.1 结构体的申明4.1.2 结构体变量的定义和初始化 4.2 结构体成…...

(免费领源码)java#Springboot#mysql旅游景点订票系统68524-计算机毕业设计项目选题推荐
摘 要 科技进步的飞速发展引起人们日常生活的巨大变化,电子信息技术的飞速发展使得电子信息技术的各个领域的应用水平得到普及和应用。信息时代的到来已成为不可阻挡的时尚潮流,人类发展的历史正进入一个新时代。在现实运用中,应用软件的工作…...
帝国cms7.5 支付升级优化版文库范文自动生成word/PDF文档付费复制下载带支付系统会员中心整站模板源码sitemap百度推送+安装教程
帝国cms7.5 支付升级优化版文库范文自动生成word/PDF文档付费复制下载带支付系统会员中心整站模板源码sitemap百度推送+安装教程 (购买本专栏可免费下载栏目内所有资源不受限制,持续发布中,需要注意的是,本专栏为批量下载专用,并无法保证某款源码或者插件绝对可用,介意不…...

【node】关于npm、yarn、npx的区别与使用
文章目录 npm (Node Package Manager):安装依赖运行脚本 npx:执行项目依赖中的命令 yarn:安装依赖eg.使用npx yarn install 的作用 npm (Node Package Manager): 用途: npm 是 Node.js 官方提供的包管理工具,用于安装、管理和分享 JavaScript 代码包。安…...

力扣0099——恢复二叉搜索树
恢复二叉搜索树 难度:中等 题目描述 给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。 示例1 输入: root [1,3,null,null,2] 输出:[3,1,null,nul…...
机器学习核心算法
目录 逻辑回归 算法原理 决策树 决策树算法概述 树的组成 决策树的训练与测试 切分特征 衡量标准--熵 信息增益 决策树构造实例 连续值问题解决 预剪枝方法 分类与回归问题解决 决策树解决分类问题步骤 决策树解决回归问题步骤 决策树代码实例 集成算法 Baggi…...

libjsoncpp 的编译和交叉编译
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

【Unity美术】如何用3DsMax做一个水桶模型
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

如何用一根网线和51单片机做简单门禁[带破解器]
仓库:https://github.com/MartinxMax/Simple_Door 支持原创是您给我的最大动力… 原理 -基础设备代码程序- -Arduino爆破器程序 or 51爆破器程序- 任意选一个都可以用… —Arduino带TFT屏幕——— —51带LCD1602——— 基础设备的最大密码长度是0x7F,因为有一位…...

在 VUE 项目中,使用 Axios 请求数据时,提示跨域,该怎么解决?
在 VUE 项目开发时,遇到个问题,正常设置使用 Axios 库请求数据时,报错提示跨域问题。 那在生产坏境下,该去怎么解决呢? 其可以通过以下几种方式去尝试解决: 1、设置允许跨域请求的响应头 1.1 在响应头中…...
1.【Vue3】前端开发引入、Vue 简介
1. 前端开发引入 1.1 前端开发前置知识 通过之前的学习,已经通过 SpringBoot 和一些三方技术完成了大事件项目的后端开发。接下来开始学习大事件项目的前端开发,前端部分借助两个框架实现: Vue3(一个 JS 框架)基于 …...

一起学习ETCD系列——运维操作之etcdctl使用
文章目录 概要一、命令二、实操2.1、基本操作2.2、watch2.3、租约2.4、分布式锁2.5、角色2.6、用户2.7、认证2.8、集群 概要 本文主要用来总结ETCD客户端ctcdctl的命令操作,在运维过程中可能常常用到的。 一、命令 etcd工具 etcdctl官方命令示例 [roottest etcd…...

Spring Security 存储密码之 JDBC
Spring Security的JdbcDaoImpl实现了UserDetailsService接口,通过使用JDBC提供支持基于用户名和密码的身份验证。 JdbcUserDetailsManager扩展了JdbcDaoImpl,通过UserDetailsManager接口提供UserDetails的管理功能。 当Spring Security配置为接受用户名/密码进行身份验证时,…...
第3章-python深度学习——(波斯美女)
第3章 神经网络入门 本章包括以下内容: 神经网络的核心组件 Keras 简介 建立深度学习工作站 使用神经网络解决基本的分类问题与回归问题 本章的目的是让你开始用神经网络来解决实际问题。你将进一步巩固在第 2 章第一个示例中学到的知识,还会将学到的…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...
