力扣0099——恢复二叉搜索树
恢复二叉搜索树
难度:中等
题目描述
给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
示例1
输入: root = [1,3,null,null,2]
输出:[3,1,null,null,2]
示例2
输入: root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
题解
因为二叉搜索树的性质可得,将其中序遍历存储到列表中,数值为单调递增,由此可以得到以下步骤
- 遍历列表,找到递增中断点
- 再次遍历列表,找到中断点应该在的位置
- 将两个数值进行交换
完成之后即为所求
想法代码
public class TreeNode
{public int val;public TreeNode left;public TreeNode right;public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null){this.val = val;this.left = left;this.right = right;}
}
class Solution
{IList<TreeNode> travelList = new List<TreeNode>();public static void Main(String[] args){TreeNode root = new TreeNode(3){left = new TreeNode(1),right = new TreeNode(4){left = new TreeNode(2)}};Solution solution = new Solution();solution.RecoverTree(root);foreach (var a in solution.travelList){Console.Write(a.val + " ");}}public void RecoverTree(TreeNode root){Travel(root);int index1 = 1;int index2 = 0;while (index1 < travelList.Count){if (travelList[index1].val > travelList[index1 - 1].val){index1++;}else{break;}}while (index2 < travelList.Count){if (travelList[index2].val > travelList[index1 - 1].val){break;}index2++;}TreeNode treeNode1 = travelList[index1 - 1];TreeNode treeNode2 = travelList[index2 - 1];int val1 = treeNode1.val;int val2 = treeNode2.val;treeNode1.val = val2;treeNode2.val = val1;}public void Travel(TreeNode root){if (root == null){return;}Travel(root.left);travelList.Add(root);Travel(root.right);}
}
avel(root.left);travelList.Add(root);Travel(root.right);}
}
相关文章:

力扣0099——恢复二叉搜索树
恢复二叉搜索树 难度:中等 题目描述 给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。 示例1 输入: root [1,3,null,null,2] 输出:[3,1,null,nul…...
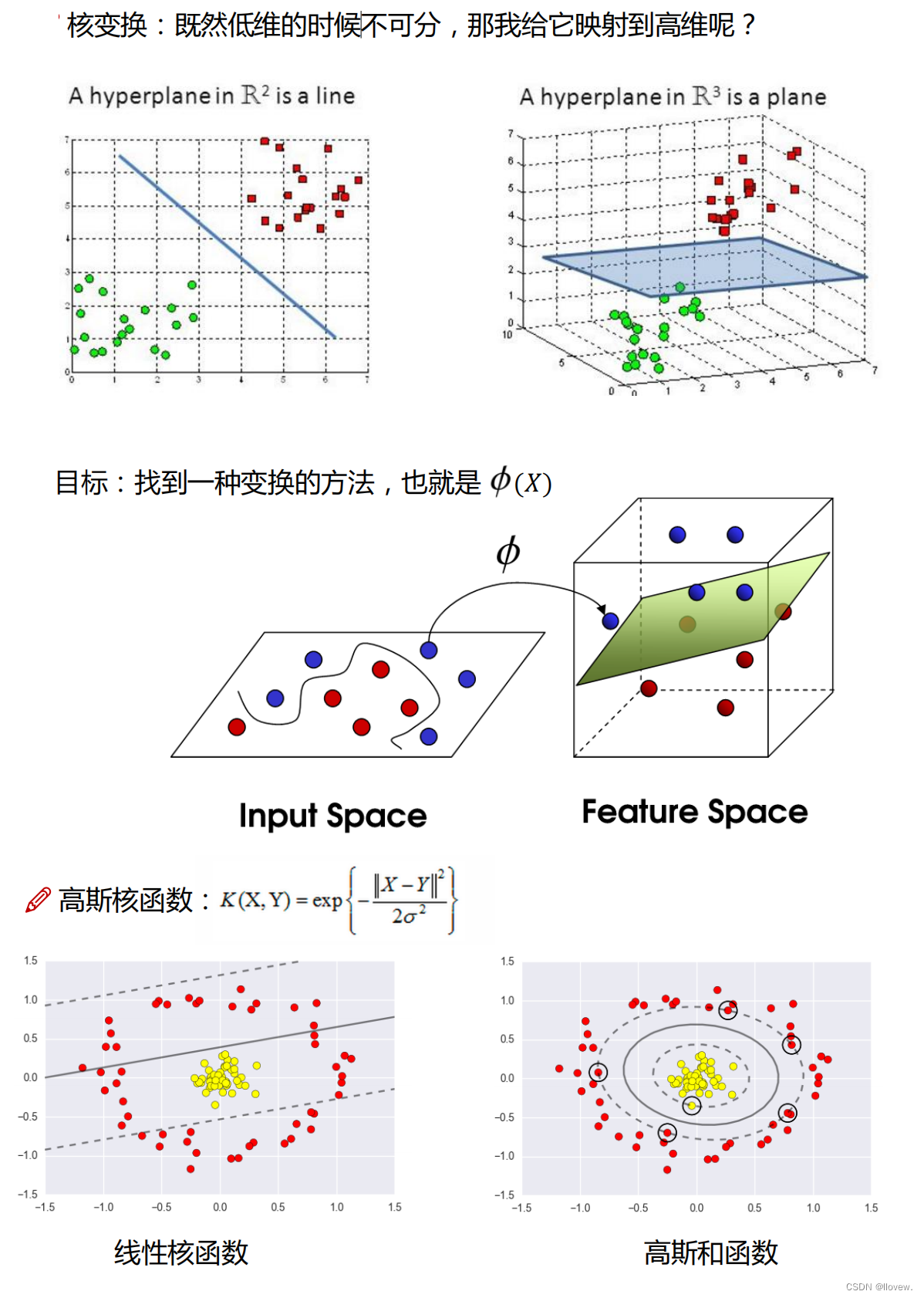
机器学习核心算法
目录 逻辑回归 算法原理 决策树 决策树算法概述 树的组成 决策树的训练与测试 切分特征 衡量标准--熵 信息增益 决策树构造实例 连续值问题解决 预剪枝方法 分类与回归问题解决 决策树解决分类问题步骤 决策树解决回归问题步骤 决策树代码实例 集成算法 Baggi…...

libjsoncpp 的编译和交叉编译
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

【Unity美术】如何用3DsMax做一个水桶模型
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

如何用一根网线和51单片机做简单门禁[带破解器]
仓库:https://github.com/MartinxMax/Simple_Door 支持原创是您给我的最大动力… 原理 -基础设备代码程序- -Arduino爆破器程序 or 51爆破器程序- 任意选一个都可以用… —Arduino带TFT屏幕——— —51带LCD1602——— 基础设备的最大密码长度是0x7F,因为有一位…...

在 VUE 项目中,使用 Axios 请求数据时,提示跨域,该怎么解决?
在 VUE 项目开发时,遇到个问题,正常设置使用 Axios 库请求数据时,报错提示跨域问题。 那在生产坏境下,该去怎么解决呢? 其可以通过以下几种方式去尝试解决: 1、设置允许跨域请求的响应头 1.1 在响应头中…...
1.【Vue3】前端开发引入、Vue 简介
1. 前端开发引入 1.1 前端开发前置知识 通过之前的学习,已经通过 SpringBoot 和一些三方技术完成了大事件项目的后端开发。接下来开始学习大事件项目的前端开发,前端部分借助两个框架实现: Vue3(一个 JS 框架)基于 …...

一起学习ETCD系列——运维操作之etcdctl使用
文章目录 概要一、命令二、实操2.1、基本操作2.2、watch2.3、租约2.4、分布式锁2.5、角色2.6、用户2.7、认证2.8、集群 概要 本文主要用来总结ETCD客户端ctcdctl的命令操作,在运维过程中可能常常用到的。 一、命令 etcd工具 etcdctl官方命令示例 [roottest etcd…...

Spring Security 存储密码之 JDBC
Spring Security的JdbcDaoImpl实现了UserDetailsService接口,通过使用JDBC提供支持基于用户名和密码的身份验证。 JdbcUserDetailsManager扩展了JdbcDaoImpl,通过UserDetailsManager接口提供UserDetails的管理功能。 当Spring Security配置为接受用户名/密码进行身份验证时,…...
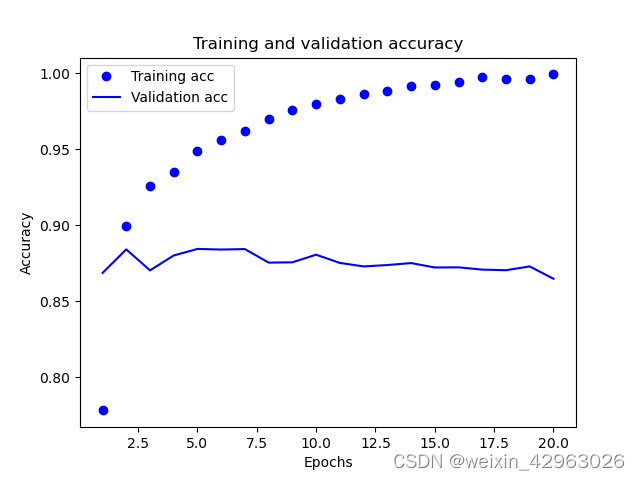
第3章-python深度学习——(波斯美女)
第3章 神经网络入门 本章包括以下内容: 神经网络的核心组件 Keras 简介 建立深度学习工作站 使用神经网络解决基本的分类问题与回归问题 本章的目的是让你开始用神经网络来解决实际问题。你将进一步巩固在第 2 章第一个示例中学到的知识,还会将学到的…...
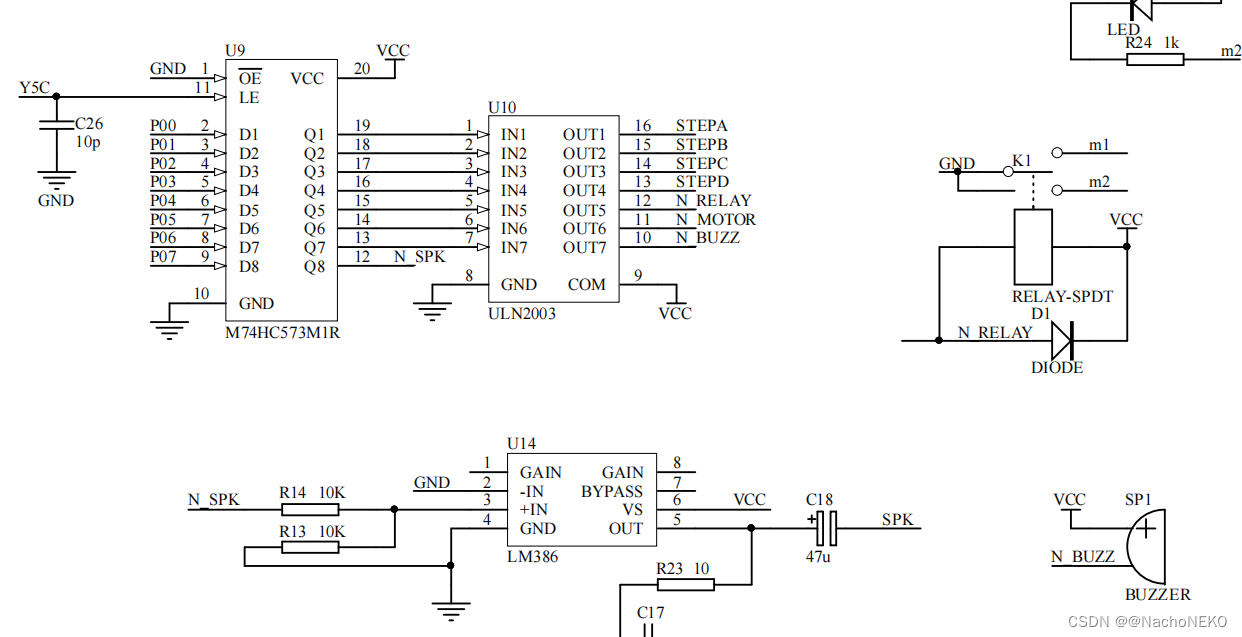
蓝桥杯备战——4.继电器/蜂鸣器
1.分析原理图 最好自己先去查查138以及ULN2003的使用方法,我这里直接讲思路。 由上图我们可以看到如果138输入ABC101,则输出Y50,此时若WR通过跳线帽接地则Y5C1 ,于是573(U9)处于输出跟随输入P0状态,此时若P061,则573输出Q71&am…...

Redis高级特性之地理空间索引
Redis的地理空间索引是一种功能强大的工具,用于存储和查询地理空间数据。这个特性主要通过Redis的地理空间数据类型 - GeoSet(地理集合)来实现。在这篇文章中,我们将探索Redis地理空间数据类型的使用和应用。 1. Redis GeoSet 简…...

R语言【taxlist】——as():将 taxlist 对象强制转换为 list 对象
Package taxlist version 0.2.4 Description 可以应用 S4 对象到 list 对象的强制转换来探索它们的内容,避免由它们的验证引起的错误。 Usage S4_to_list(x) Argument 参数【x】:一个 taxlist 类对象或任意 S4 类。 Details 将 taxlist 对象强制转换…...

使用POI生成word文档的table表格
文章目录 使用POI生成word文档的table表格1. 引入maven依赖2. 生成table的两种方式介绍2.1 生成一行一列的table2.2 生成固定行列的table2.3 table合并列2.4 创建多个table存在的问题 使用POI生成word文档的table表格 1. 引入maven依赖 <dependency><groupId>org.…...

C# 继承、多态性、抽象和接口详解:从入门到精通
C# 继承 在 C# 中,可以将字段和方法从一个类继承到另一个类。我们将“继承概念”分为两类: 派生类(子类) - 从另一个类继承的类基类(父类) - 被继承的类 要从一个类继承,使用 : 符号。 在以…...
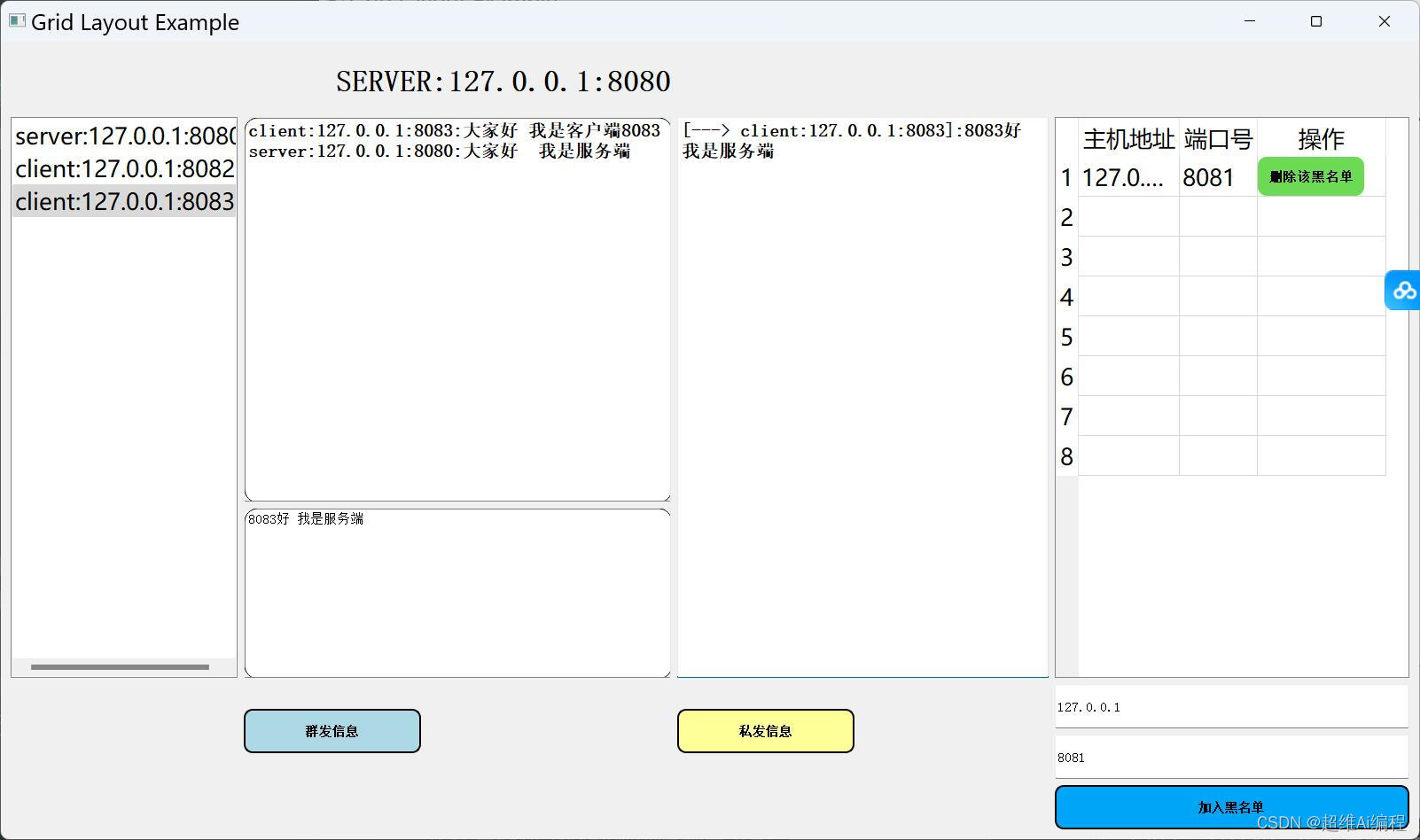
python在线聊天室(带聊天保存)
python Socket在线聊天室(带聊天保存) 需求功能 1.聊天信息保存功能(服务端会把信息保存到一个txt里面) 2.使用pyqt5框架作为一个可视化界面 3.具备一个服务端和多个客户端的功能 4.具备离线加入黑名单(离线踢出) 5.具备在线加入黑名单(在线加入黑名单被踢出) 6.具备群聊功能…...

jenkins+gitlab实现Android自动打包填坑之旅
一.背景 1.首先你需要知道你想要实现的Android自动打包的Android项目的一些环境配置及需要使用的一些开发版本。 声明:本文 Android项目基于:1.jdk11 2.SDK无要求 3.gradle无要求(同Manven一样为项目自动化构建开源工具) 注&am…...

洛谷B3625迷宫寻路
迷宫寻路 题目描述 机器猫被困在一个矩形迷宫里。 迷宫可以视为一个 n m n\times m nm 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。 机器猫初始时位于 ( 1 , 1 ) (1, 1) (1,1) 的位置,问能否…...
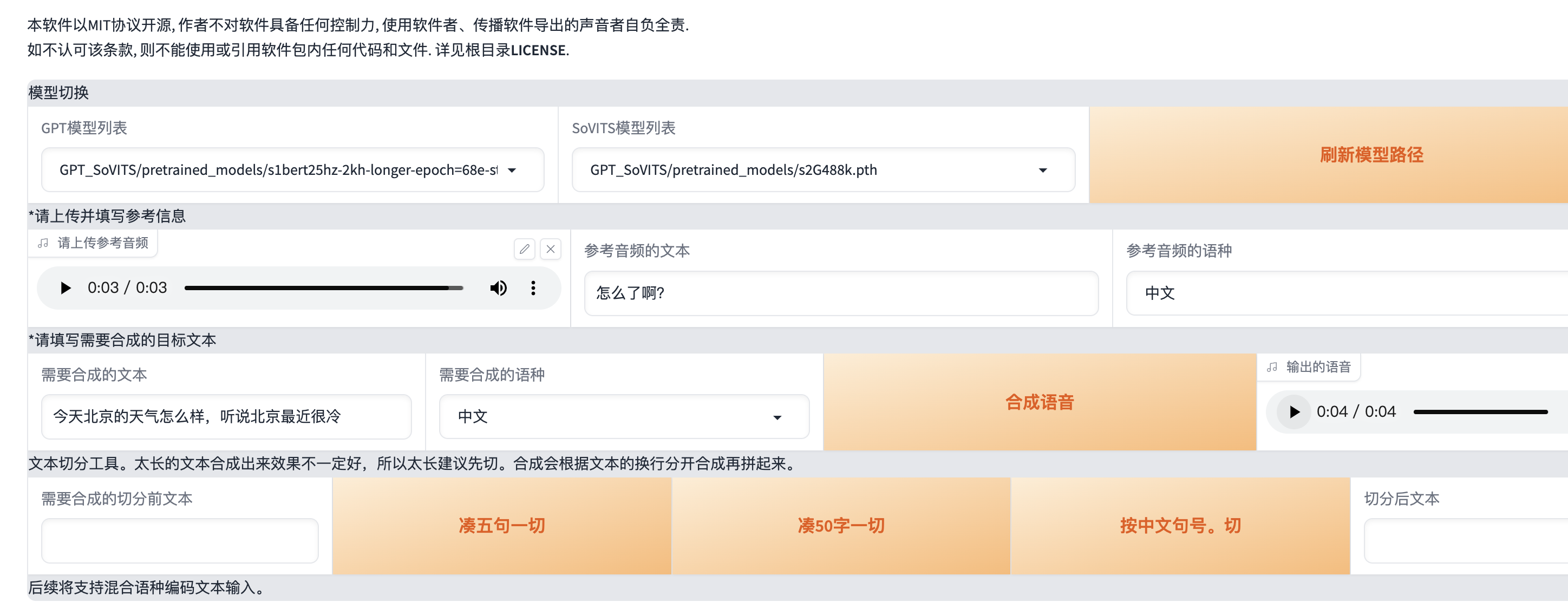
GPT-SoVITS 测试
开箱直用版(使用 AutoDL) step1 打开地址 https://www.codewithgpu.com/i/RVC-Boss/GPT-SoVITS/GPT-SoVITS-Official 选择 AutoDL创建实例,选择 3080ti 机器 step2 创建好实例之后,进入命令行,输入命令 echo {}>…...
人工智能:更多有用的 Python 库
目录 前言 推荐 JupyterLab 入门 复杂的矩阵运算 其它人工智能和机器学习的 Python 库 前言 在这篇文章中,我们将了解更多的矩阵操作,同时再介绍几个人工智能 Python 库。 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&#x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
