LeetCode:376.摆动序列
个人主页:仍有未知等待探索-CSDN博客
专题分栏:算法_仍有未知等待探索的博客-CSDN博客
题目链接:376. 摆动序列 - 力扣(LeetCode)
一、题目
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。- 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组
nums,返回nums中作为 摆动序列 的 最长子序列的长度 。示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9] 输出:2提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
二、理解
我们要求摆动序列的最大子序列(可以进行删除操作,创造子序列)

我们只需要记录每段是上升的还是下降的,然后如果连续的两个序列不同的话,就进行记录。
(还有一种用峰值来判断的方法比较繁琐)
三、代码
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int ans = 0;// 用来记录答案int f = 0;// 标记位, 用来标记上一个状态,是升序还是降序// 从第二个数开始进行,因为第一个数总是会加到答案里面去for (int i = 1; i < nums.size(); i ++ ){// 该序列是升序,但是上一个序列不能为升序if (nums[i - 1] < nums[i] && f != 1){ans ++;f = 1;// 升序}else if (nums[i - 1] > nums[i] && f != 2){ans ++;f = 2;// 降序}}// 把第一个数进行包含return ans + 1;}
};谢谢大家!
相关文章:

LeetCode:376.摆动序列
个人主页:仍有未知等待探索-CSDN博客 专题分栏:算法_仍有未知等待探索的博客-CSDN博客 题目链接:376. 摆动序列 - 力扣(LeetCode) 一、题目 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称…...
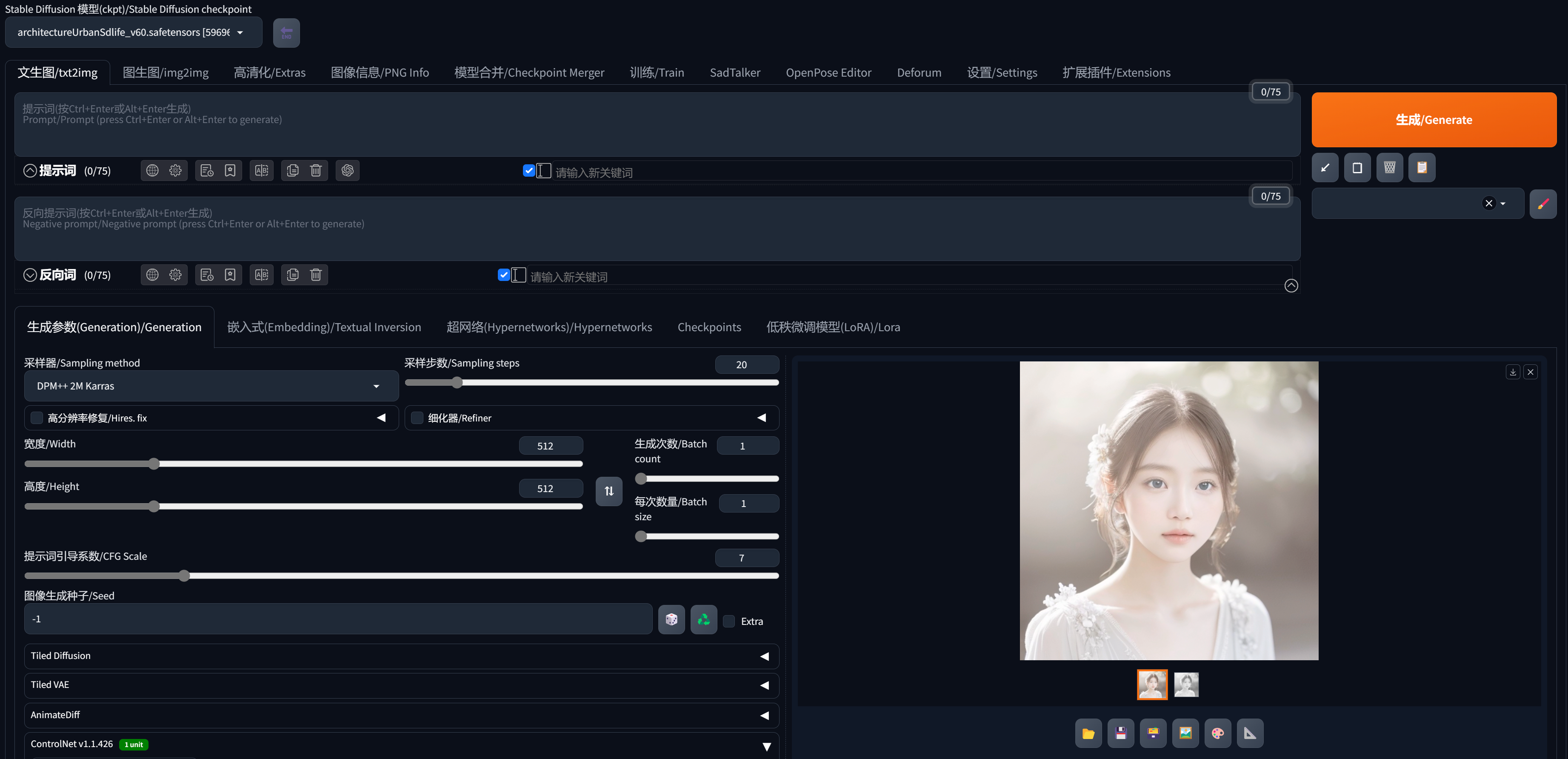
Stable Diffusion插件Recolor实现黑白照片上色
今天跟大家分享一个使用Recolor插件通过SD实现老旧照片轻松变彩色,Recolor翻译过来的含义就是重上色,该模型可以保持图片的构图,它只会负责上色,图片不会发生任何变化。 一:插件下载地址 https://github.com/pkuliyi…...

Android 音频焦点管理
前言 前面写过一篇类似的文章,没写完,今天再详细描述一下。 Android音频焦点申请处理 音频焦点管理的意义 两个或两个以上的 Android 应用可同时向同一输出流播放音频。系统会将所有音频流混合在一起。虽然这是一项出色的技术,但却会给用…...
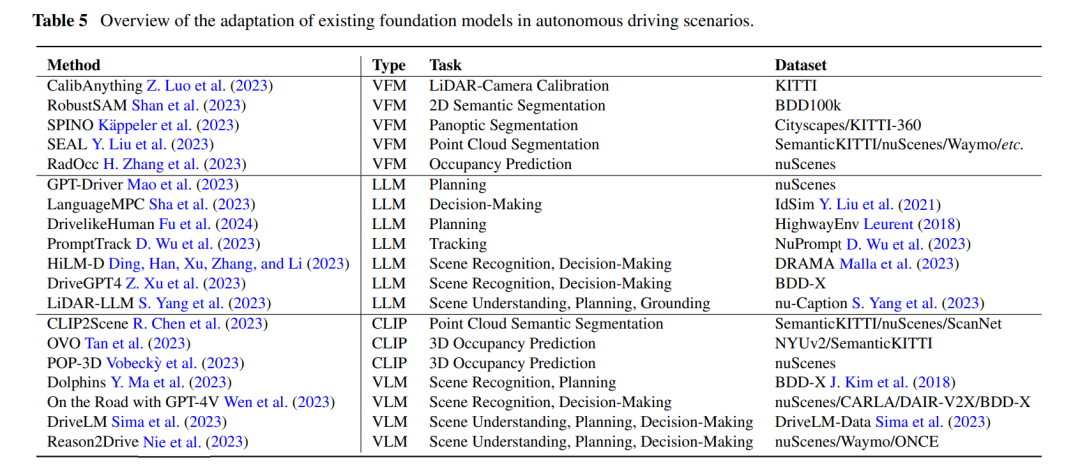
大模型+自动驾驶
论文:https://arxiv.org/pdf/2401.08045.pdf 大型基础模型的兴起,它们基于广泛的数据集进行训练,正在彻底改变人工智能领域的面貌。例如SAM、DALL-E2和GPT-4这样的模型通过提取复杂的模式,并在不同任务中有效地执行,从…...
openssl3.2 - 测试程序的学习 - test\aesgcmtest.c
文章目录 openssl3.2 - 测试程序的学习 - test\aesgcmtest.c概述笔记能学到的流程性内容END openssl3.2 - 测试程序的学习 - test\aesgcmtest.c 概述 openssl3.2 - 测试程序的学习 aesgcmtest.c 工程搭建时, 发现没有提供 test_get_options(), cleanup_tests(), 需要自己补上…...

C语言——操作符详解2
目录 0.过渡0.1 不创建临时变量,交换两数0.2 求整数转成二进制后1的总数 1.单目表达式2. 逗号表达式3. 下标访问[ ]、函数调用( )3.1 下标访问[ ]3.2 函数调用( ) 4. 结构体成员访问操作符4.1 结构体4.1.1 结构体的申明4.1.2 结构体变量的定义和初始化 4.2 结构体成…...

(免费领源码)java#Springboot#mysql旅游景点订票系统68524-计算机毕业设计项目选题推荐
摘 要 科技进步的飞速发展引起人们日常生活的巨大变化,电子信息技术的飞速发展使得电子信息技术的各个领域的应用水平得到普及和应用。信息时代的到来已成为不可阻挡的时尚潮流,人类发展的历史正进入一个新时代。在现实运用中,应用软件的工作…...
帝国cms7.5 支付升级优化版文库范文自动生成word/PDF文档付费复制下载带支付系统会员中心整站模板源码sitemap百度推送+安装教程
帝国cms7.5 支付升级优化版文库范文自动生成word/PDF文档付费复制下载带支付系统会员中心整站模板源码sitemap百度推送+安装教程 (购买本专栏可免费下载栏目内所有资源不受限制,持续发布中,需要注意的是,本专栏为批量下载专用,并无法保证某款源码或者插件绝对可用,介意不…...

【node】关于npm、yarn、npx的区别与使用
文章目录 npm (Node Package Manager):安装依赖运行脚本 npx:执行项目依赖中的命令 yarn:安装依赖eg.使用npx yarn install 的作用 npm (Node Package Manager): 用途: npm 是 Node.js 官方提供的包管理工具,用于安装、管理和分享 JavaScript 代码包。安…...

力扣0099——恢复二叉搜索树
恢复二叉搜索树 难度:中等 题目描述 给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。 示例1 输入: root [1,3,null,null,2] 输出:[3,1,null,nul…...
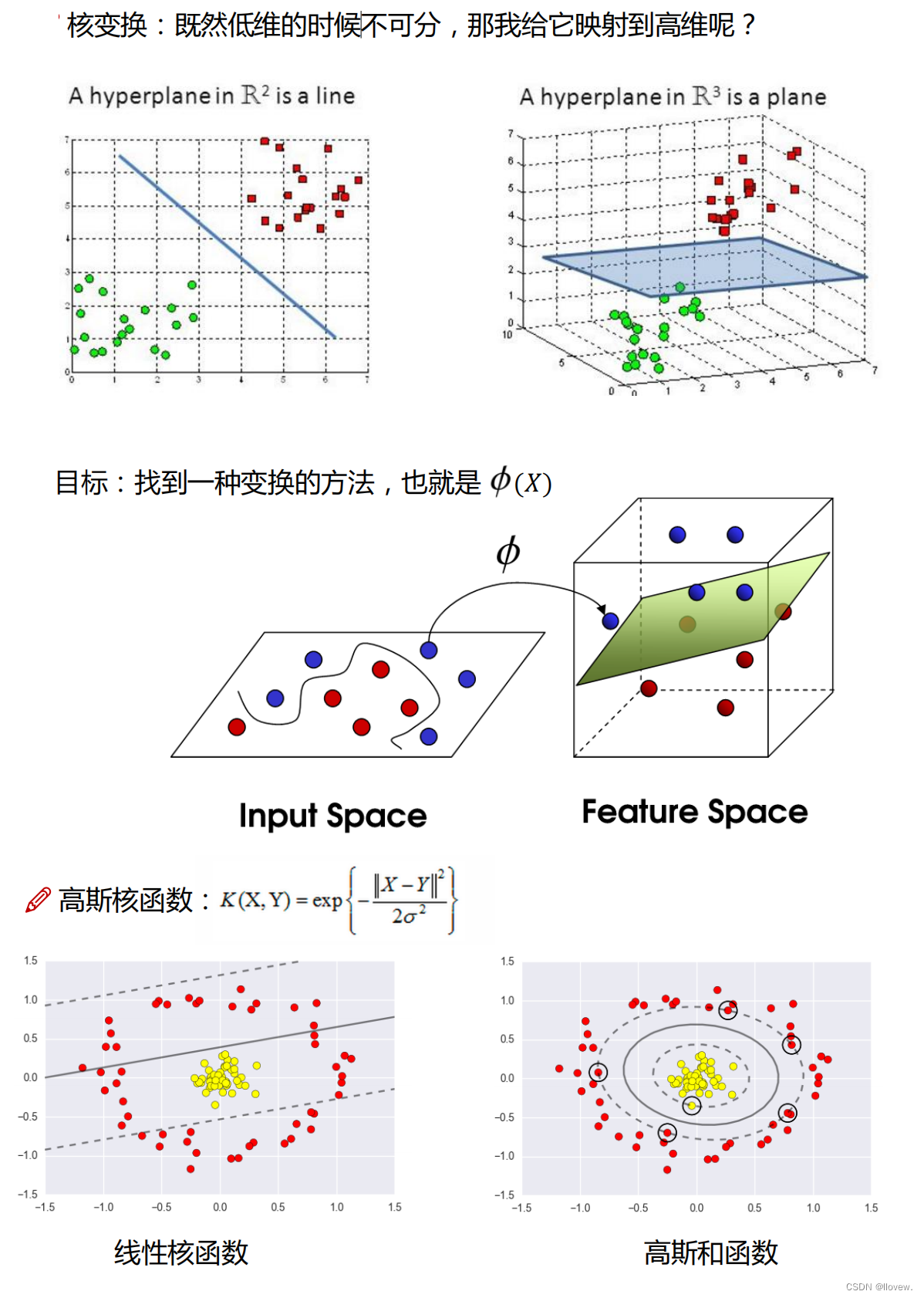
机器学习核心算法
目录 逻辑回归 算法原理 决策树 决策树算法概述 树的组成 决策树的训练与测试 切分特征 衡量标准--熵 信息增益 决策树构造实例 连续值问题解决 预剪枝方法 分类与回归问题解决 决策树解决分类问题步骤 决策树解决回归问题步骤 决策树代码实例 集成算法 Baggi…...

libjsoncpp 的编译和交叉编译
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

【Unity美术】如何用3DsMax做一个水桶模型
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

如何用一根网线和51单片机做简单门禁[带破解器]
仓库:https://github.com/MartinxMax/Simple_Door 支持原创是您给我的最大动力… 原理 -基础设备代码程序- -Arduino爆破器程序 or 51爆破器程序- 任意选一个都可以用… —Arduino带TFT屏幕——— —51带LCD1602——— 基础设备的最大密码长度是0x7F,因为有一位…...

在 VUE 项目中,使用 Axios 请求数据时,提示跨域,该怎么解决?
在 VUE 项目开发时,遇到个问题,正常设置使用 Axios 库请求数据时,报错提示跨域问题。 那在生产坏境下,该去怎么解决呢? 其可以通过以下几种方式去尝试解决: 1、设置允许跨域请求的响应头 1.1 在响应头中…...
1.【Vue3】前端开发引入、Vue 简介
1. 前端开发引入 1.1 前端开发前置知识 通过之前的学习,已经通过 SpringBoot 和一些三方技术完成了大事件项目的后端开发。接下来开始学习大事件项目的前端开发,前端部分借助两个框架实现: Vue3(一个 JS 框架)基于 …...

一起学习ETCD系列——运维操作之etcdctl使用
文章目录 概要一、命令二、实操2.1、基本操作2.2、watch2.3、租约2.4、分布式锁2.5、角色2.6、用户2.7、认证2.8、集群 概要 本文主要用来总结ETCD客户端ctcdctl的命令操作,在运维过程中可能常常用到的。 一、命令 etcd工具 etcdctl官方命令示例 [roottest etcd…...

Spring Security 存储密码之 JDBC
Spring Security的JdbcDaoImpl实现了UserDetailsService接口,通过使用JDBC提供支持基于用户名和密码的身份验证。 JdbcUserDetailsManager扩展了JdbcDaoImpl,通过UserDetailsManager接口提供UserDetails的管理功能。 当Spring Security配置为接受用户名/密码进行身份验证时,…...
第3章-python深度学习——(波斯美女)
第3章 神经网络入门 本章包括以下内容: 神经网络的核心组件 Keras 简介 建立深度学习工作站 使用神经网络解决基本的分类问题与回归问题 本章的目的是让你开始用神经网络来解决实际问题。你将进一步巩固在第 2 章第一个示例中学到的知识,还会将学到的…...
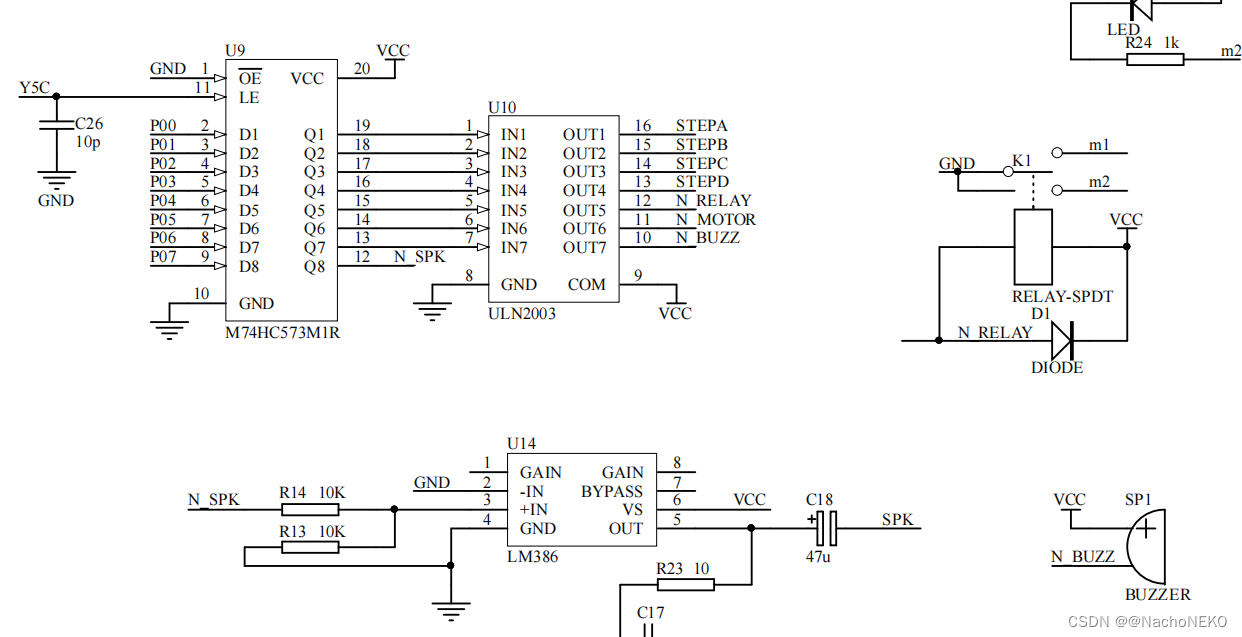
蓝桥杯备战——4.继电器/蜂鸣器
1.分析原理图 最好自己先去查查138以及ULN2003的使用方法,我这里直接讲思路。 由上图我们可以看到如果138输入ABC101,则输出Y50,此时若WR通过跳线帽接地则Y5C1 ,于是573(U9)处于输出跟随输入P0状态,此时若P061,则573输出Q71&am…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
