数据结构篇-03:堆实现优先级队列
本文着重在于讲解用 “堆实现优先级队列” 以及优先级队列的应用,在本文所举的例子中,可能使用优先级队列来解并不是最优解法,但是正如我所说的:本文着重在于讲解“堆实现优先级队列”
堆实现优先级队列
堆的主要应用有两个,一个是排序方法[堆排序],一个是数据结构 [优先级队列]。
我们会发现,人们总是把二叉堆画成一棵二叉树。其实二叉堆在逻辑上就是一种特殊的二叉树,只不过存储在数组里。
比如 arr 是一个字符数组,注意数组的第一个索引 0 空着不用:

为什么索引 0 空着不用?
为了方便计算父节点和子节点的索引,通常会将数组的第一个元素存储在索引1的位置上,而不是索引0。这样可以通过简单的数学计算得到父节点和子节点的索引,而无需进行额外的操作。
具体来说,在该代码中:
根据完全二叉树的性质,如果某个节点的索引为i,则其左子节点的索引为2i,右子节点的索引为2i + 1。
如果索引从1开始,则根节点的索引为1,其左子节点的索引为2,右子节点的索引为3。
如果索引从0开始,则根节点的索引为0,其左子节点的索引为1,右子节点的索引为2。
因此,为了避免对索引的调整和计算,通常会将数组的第一个元素放在索引1的位置上,并从索引1开始使用。这也是为什么在这段代码中索引0不被使用的原因。
请注意,这种索引方式只是约定俗成的一种做法,并非固定规定。在某些情况下,也可以使用索引从0开始的方式实现堆或优先队列。这取决于具体的实现和需求。
构建优先级队列
可以使用 最大堆/最小堆 来构建优先级队列,当插入或者删除元素的时候,元素会自动排序,这底层的原理就是二叉堆的操作。
当我们使用一个最大堆来实现一个优先级队列时,堆顶元素总是数组中的最大值。这背后就是由[上浮] 和 [下沉] 两个操作来维护堆结构的。
维护堆结构的操作——swim和sink
我们要讲的是最大堆,每个节点都比它的两个子节点大,但是在插入元素和删除元素时,难免破坏堆的性质,这就需要通过这两个操作来恢复堆的性质了。
对于最大堆,会破坏堆性质的有两种情况:
1、如果某个节点 A 比它的子节点(中的一个)小,那么 A 就不配做父节点,应该下去,下面那个更大的节点上来做父节点,这就是对 A 进行下沉。
2、如果某个节点 A 比它的父节点大,那么 A 不应该做子节点,应该把父节点换下来,自己去做父节点,这就是对 A 的上浮。
当然,错位的节点 A 可能要上浮(或下沉)很多次,才能到达正确的位置,恢复堆的性质。所以代码中肯定有一个 while 循环。
上浮操作的实现:
private void swim(int x) {// 索引 1 是堆顶//判断:x不是堆顶元素且x大于其父结点while (x > 1 && less(parent(x), x)) {// 交换x的父结点与x下标元素swap(parent(x), x);//将父节点的索引给x,指针指向xx = parent(x);}}下沉操作的实现:
private void sink(int x) {// size 是堆的最后一个索引//判断:当x的左节点不是堆底元素时while (left(x) <= size) {// 先假设左边节点较大int max = left(x);// 如果右边节点存在,比一下大小//判断:右节点不是堆底元素且右节点值大于max的值if (right(x) <= size && less(max, right(x)))max = right(x);// 结点 x 比俩孩子都大,就不必下沉了if (less(max, x)) break;// 否则,不符合最大堆的结构,下沉 x 结点swap(x, max);x = max;}}数据结构的基本操作——增删查改
增加操作
将元素插到堆的底部,然后上浮到对应位置
public void insert(Key e) {size++;// 先把新元素加到最后pq[size] = e;// 然后让它上浮到正确的位置swim(size);}删除操作
将要删除的元素与堆底元素对调,然后删除堆底元素。最后维护堆结构
public Key delMax() {// 最大堆的堆顶就是最大元素Key max = pq[1];// 把这个最大元素换到最后,删除之swap(1, size);pq[size] = null;size--;// 让 pq[1] 下沉到正确位置sink(1);return max;}查看操作
查看最大值,直接返回堆顶元素即可
public Key max() {return pq[1];}整体代码
public class MaxPQ<Key extends Comparable<Key>> {/*完全二叉树中的索引下标是可以计算出来的*/// 父节点的索引int parent(int root) {return root / 2;}// 左孩子的索引int left(int root) {return root * 2;}// 右孩子的索引int right(int root) {return root * 2 + 1;}// 存储元素的数组private Key[] pq;// 当前 Priority Queue 中的元素个数private int size = 0;public MaxPQ(int cap) {// 索引 0 不用,所以多分配一个空间pq = (Key[]) new Comparable[cap + 1];}/* 返回当前队列中最大元素 */public Key max() {return pq[1];}/* 插入元素 e */public void insert(Key e) {size++;// 先把新元素加到最后pq[size] = e;// 然后让它上浮到正确的位置swim(size);}/* 删除并返回当前队列中最大元素 */public Key delMax() {// 最大堆的堆顶就是最大元素Key max = pq[1];// 把这个最大元素换到最后,删除之swap(1, size);pq[size] = null;size--;// 让 pq[1] 下沉到正确位置sink(1);return max;}/* 上浮第 x 个元素,以维护最大堆性质 */private void swim(int x) {// 如果浮到堆顶,就不能再上浮了//因为是从索引1开始的,所以索引1是堆顶//判断:当x不是堆顶且x的父结点小于x时while (x > 1 && less(parent(x), x)) {// 如果第 x 个元素比上层大// 交换数组下标元素swap(parent(x), x);x = parent(x);}}/* 下沉第 x 个元素,以维护最大堆性质 */private void sink(int x) {// 如果沉到堆底,就沉不下去了while (left(x) <= size) {// 先假设左边节点较大int max = left(x);// 如果右边节点存在,比一下大小if (right(x) <= size && less(max, right(x)))max = right(x);// 结点 x 比俩孩子都大,就不必下沉了if (less(max, x)) break;// 否则,不符合最大堆的结构,下沉 x 结点swap(x, max);x = max;}}/* 交换数组的两个元素 */private void swap(int i, int j) {Key temp = pq[i];pq[i] = pq[j];pq[j] = temp;}/* pq[i] 是否比 pq[j] 小? */private boolean less(int i, int j) {return pq[i].compareTo(pq[j]) < 0;}
}
附注1:对<Key extends Comparable<Key>>的解释
<Key extends Comparable<Key>>是Java的泛型语法。它指示了MaxPQ类使用一个类型参数Key,并且要求这个类型Key必须实现了Comparable<Key>接口。
Comparable<Key>接口是Java中定义的一个泛型接口,用于比较两个对象的顺序。它要求实现类具有比较自身与其他对象的能力,并返回一个整数值表示它们的相对顺序。
通过实现Comparable接口,我们可以在堆和优先级队列中比较元素的大小,以维护它们的排序规则。
在这段代码中,Key作为泛型参数限制了存储在pq数组中的元素类型必须实现Comparable接口,以便能够进行比较操作(例如使用compareTo方法)。这样做可以确保我们能够正确地进行插入、删除和获取最大元素等操作,使得堆和优先级队列能够按照特定的顺序进行排序和处理。
附注2:对“pq = (Key[]) new Comparable[cap + 1]”的解释
在这段代码中,pq = (Key[]) new Comparable[cap + 1];是用来创建一个泛型数组的操作。
首先,我们需要了解在Java中创建泛型数组的限制。由于Java的类型擦除机制,无法直接创建一个具体类型的泛型数组。
因此,我们只能通过创建一个非泛型数组,然后将其转换为泛型数组。
在这段代码中,new Comparable[cap + 1]创建了一个长度为cap + 1的非泛型数组,
并且元素的类型是Comparable接口。这个数组在内存中被分配了空间。
然后,(Key[])表示进行了一个类型转换。
因为我们知道该数组是要存储Key类型的元素,所以我们将其强制转换为泛型数组类型Key[]。
最后,将转换后的泛型数组赋值给变量pq,使得pq引用这个泛型数组。
需要注意的是,在进行强制类型转换时,存在一定的风险。
如果实际存储在数组中的元素类型不符合泛型参数Key的约束条件,可能会导致运行时错误。
因此,在使用该代码时,应确保泛型参数和实际存储的元素类型是匹配的。*/
优先级队列的应用
力扣215. 数组中的第K个最大元素
思路
使用数组构造一个最大堆,然后选出第k大的元素
构建最大堆
// 构建最大堆public void buildMaxHeap(int[] a, int heapSize) {for (int i = heapSize / 2; i >= 0; --i) {maxHeapify(a, i, heapSize); // 对每个非叶子节点进行调整,使其满足最大堆的性质}}// 调整以i为根节点的子树,使其满足最大堆的性质public void maxHeapify(int[] a, int i, int heapSize) {//计算左右节点的下标int left = i * 2 + 1, right = i * 2 + 2, largest = i;// 下沉操作:比较节点i与其左右子节点的值,找到最大值// 先与左节点对比if (left < heapSize && a[left] > a[largest]) {largest = left;}// 再与右节点对比if (right < heapSize && a[right] > a[largest]) {largest = right;}if (largest != i) {swap(a, i, largest); // 将节点i与最大值节点交换位置maxHeapify(a, largest, heapSize); // 继续向下调整以保持最大堆的性质}}// 交换数组中两个元素的位置public void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}问题1: “for (int i = heapSize / 2; i >= 0; --i)”是什么意思?
在构建最大堆时,我们只需要对非叶子节点进行调整,而不需要对叶子节点进行调整。这是因为堆的性质决定了,一个完全二叉树的叶子节点已经满足最大堆的条件,即叶子节点的值不会比其父节点更大。
考虑到完全二叉树的特点,具有n/2个节点是非叶子节点,其中n是堆中元素的总数。比如下标为i的元素,其左节点为 2i,右节点为 2i+1,所以对n个节点来说,只能有n/2个节点是非叶子节点。
所以,我们可以从最后一个非叶子节点(索引为n/2 - 1)开始,向前逐个调用maxHeapify方法,将每个节点及其子树调整为最大堆。
由于最大堆的性质要求父节点的值大于或等于其子节点的值,通过逐层向上调整非叶子节点,我们能够确保整个堆都满足最大堆的要求。
因此,在buildMaxHeap方法中,我们只对非叶子节点进行调整,以节省时间
选出第k大的元素
选出第k大的元素的方法是取出堆顶的元素,将其与堆底元素交换,然后缩小堆,重新维护堆结构。就相当于把堆顶的最大元素删除了。
正数第k个元素就是倒数的第 length - k + 1个元素,所以我们将后面length - k + 1个元素与堆顶元素交换即可
public int findKthLargest(int[] nums, int k) {int heapSize = nums.length;buildMaxHeap(nums, heapSize); // 构建最大堆for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {swap(nums, 0, i); // 将堆顶元素与当前未排序部分的最后一个元素交换--heapSize; // 缩小堆的大小maxHeapify(nums, 0, heapSize); // 调整堆使其继续满足最大堆的性质}return nums[0]; // 返回第k个最大元素(堆顶元素)}整体代码
class Solution {public int findKthLargest(int[] nums, int k) {int heapSize = nums.length;buildMaxHeap(nums, heapSize); // 构建最大堆for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {swap(nums, 0, i); // 将堆顶元素与当前未排序部分的最后一个元素交换--heapSize; // 缩小堆的大小maxHeapify(nums, 0, heapSize); // 调整堆使其继续满足最大堆的性质}return nums[0]; // 返回第k个最大元素(堆顶元素)}// 构建最大堆public void buildMaxHeap(int[] a, int heapSize) {for (int i = heapSize / 2; i >= 0; --i) {maxHeapify(a, i, heapSize); // 对每个非叶子节点进行调整,使其满足最大堆的性质}}// 调整以i为根节点的子树,使其满足最大堆的性质public void maxHeapify(int[] a, int i, int heapSize) {//计算左右节点的下标int left = i * 2 + 1, right = i * 2 + 2, largest = i;// 下沉操作:比较节点i与其左右子节点的值,找到最大值// 先与左节点对比if (left < heapSize && a[left] > a[largest]) {largest = left;}// 再与右节点对比if (right < heapSize && a[right] > a[largest]) {largest = right;}if (largest != i) {swap(a, i, largest); // 将节点i与最大值节点交换位置maxHeapify(a, largest, heapSize); // 继续向下调整以保持最大堆的性质}}// 交换数组中两个元素的位置public void swap(int[] a, int i, int j) {int temp = a[i];a[i] = a[j];a[j] = temp;}
}力扣347. 前 K 个高频元素
使用哈希表记录每个元素与其出现次数的映射关系
构建一个大小为k的小根堆,如果不足k个元素就直接将当前数字加入到堆中
否则判断堆中的最小值是否小于当前数字的出现次数,如果堆中的最小值小于当前数字出现次数,说明目前的堆顶元素不在前k个高频元素中,将其弹出并将当前数字加入到堆中
import java.util.*;class Solution {public int[] topKFrequent(int[] nums, int k) {// 统计每个数字出现的次数Map<Integer, Integer> counter = new HashMap<>();for (int num : nums) {counter.put(num, counter.getOrDefault(num, 0) + 1);}// 定义小根堆,根据数字频率自小到大排序Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> counter.get(v1) - counter.get(v2));// 遍历数组,维护一个大小为 k 的小根堆:// 不足 k 个直接将当前数字加入到堆中;否则判断堆中的最小次数是否小于当前数字的出现次数,// 若是,则删掉堆中出现次数最少的一个数字,将当前数字加入堆中。for (int num : counter.keySet()) {if (pq.size() < k) {pq.offer(num);} else if (counter.get(pq.peek()) < counter.get(num)) {pq.poll();pq.offer(num);}}// 构造返回结果int[] res = new int[k];int idx = 0;for (int num : pq) {res[idx++] = num;}return res;}
}
相关文章:

数据结构篇-03:堆实现优先级队列
本文着重在于讲解用 “堆实现优先级队列” 以及优先级队列的应用,在本文所举的例子中,可能使用优先级队列来解并不是最优解法,但是正如我所说的:本文着重在于讲解“堆实现优先级队列” 堆实现优先级队列 堆的主要应用有两个&…...
linux clickhouse 安装
1、官网下载clickhouse安装包 下载地址, clickhouse分lts和stable版本,lts是长期版本,一般选择安装lts版本。 其中clickhouse-server是clickhouse服务,就是用来访问数据存储数据,clickhouse-client是用来通过命令访问数…...

【游戏客户端开发的进阶路线】
*** 游戏客户端开发的进阶路线 春招的脚步越来越近,我们注意到越来越多的同学们都在积极学习游戏开发,希望能在这个充满活力的行业中大展拳脚。 当我们思考如何成为游戏开发领域的佼佼者时,关键在于如何有效规划学习路径。 🤔 我…...
vue3+naiveUI二次封装的v-model 联动输入框
根据官网说明使用 源码 <template><div class"clw-input pt-3"><n-inputref"input":value"modelValue":type"type":title"title"clearable:disabled"disabled":size"size"placeholder&…...
百度Apollo | 实车自动驾驶:感知、决策、执行的无缝融合
🎬 鸽芷咕:个人主页 🔥 个人专栏:《linux深造日志》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下…...

DAY31:贪心算法入门455、53、376
理论基础 贪心算法的基本思路是通过局部最优从而达到全局最优,但是有时候局部最优并不一定导致全局最优,这样就需要动态规划的方法。但一部分题目是能通过贪心得到的。贪心的证明一般用到数学归纳法和反证法。在实际的问题中,没有统一的代码…...

LeetCode:376.摆动序列
个人主页:仍有未知等待探索-CSDN博客 专题分栏:算法_仍有未知等待探索的博客-CSDN博客 题目链接:376. 摆动序列 - 力扣(LeetCode) 一、题目 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称…...
Stable Diffusion插件Recolor实现黑白照片上色
今天跟大家分享一个使用Recolor插件通过SD实现老旧照片轻松变彩色,Recolor翻译过来的含义就是重上色,该模型可以保持图片的构图,它只会负责上色,图片不会发生任何变化。 一:插件下载地址 https://github.com/pkuliyi…...

Android 音频焦点管理
前言 前面写过一篇类似的文章,没写完,今天再详细描述一下。 Android音频焦点申请处理 音频焦点管理的意义 两个或两个以上的 Android 应用可同时向同一输出流播放音频。系统会将所有音频流混合在一起。虽然这是一项出色的技术,但却会给用…...
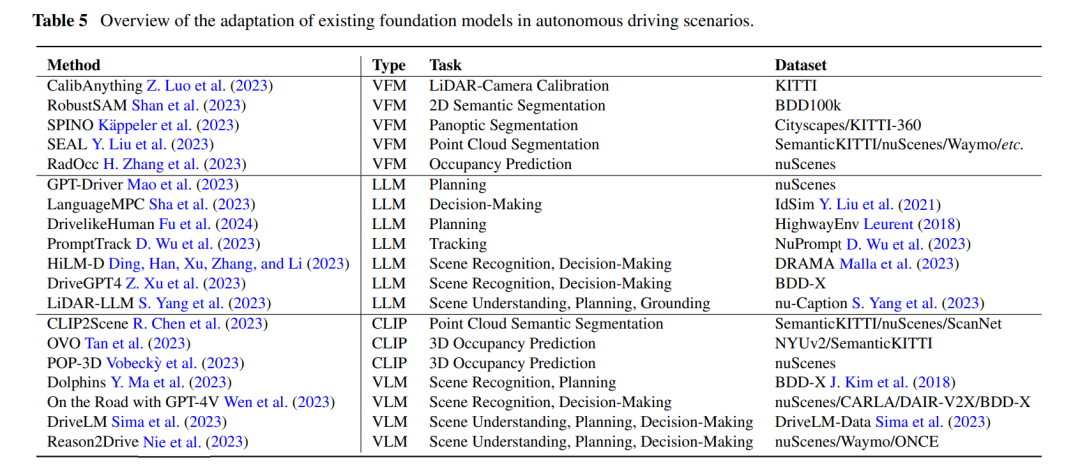
大模型+自动驾驶
论文:https://arxiv.org/pdf/2401.08045.pdf 大型基础模型的兴起,它们基于广泛的数据集进行训练,正在彻底改变人工智能领域的面貌。例如SAM、DALL-E2和GPT-4这样的模型通过提取复杂的模式,并在不同任务中有效地执行,从…...
openssl3.2 - 测试程序的学习 - test\aesgcmtest.c
文章目录 openssl3.2 - 测试程序的学习 - test\aesgcmtest.c概述笔记能学到的流程性内容END openssl3.2 - 测试程序的学习 - test\aesgcmtest.c 概述 openssl3.2 - 测试程序的学习 aesgcmtest.c 工程搭建时, 发现没有提供 test_get_options(), cleanup_tests(), 需要自己补上…...

C语言——操作符详解2
目录 0.过渡0.1 不创建临时变量,交换两数0.2 求整数转成二进制后1的总数 1.单目表达式2. 逗号表达式3. 下标访问[ ]、函数调用( )3.1 下标访问[ ]3.2 函数调用( ) 4. 结构体成员访问操作符4.1 结构体4.1.1 结构体的申明4.1.2 结构体变量的定义和初始化 4.2 结构体成…...

(免费领源码)java#Springboot#mysql旅游景点订票系统68524-计算机毕业设计项目选题推荐
摘 要 科技进步的飞速发展引起人们日常生活的巨大变化,电子信息技术的飞速发展使得电子信息技术的各个领域的应用水平得到普及和应用。信息时代的到来已成为不可阻挡的时尚潮流,人类发展的历史正进入一个新时代。在现实运用中,应用软件的工作…...
帝国cms7.5 支付升级优化版文库范文自动生成word/PDF文档付费复制下载带支付系统会员中心整站模板源码sitemap百度推送+安装教程
帝国cms7.5 支付升级优化版文库范文自动生成word/PDF文档付费复制下载带支付系统会员中心整站模板源码sitemap百度推送+安装教程 (购买本专栏可免费下载栏目内所有资源不受限制,持续发布中,需要注意的是,本专栏为批量下载专用,并无法保证某款源码或者插件绝对可用,介意不…...

【node】关于npm、yarn、npx的区别与使用
文章目录 npm (Node Package Manager):安装依赖运行脚本 npx:执行项目依赖中的命令 yarn:安装依赖eg.使用npx yarn install 的作用 npm (Node Package Manager): 用途: npm 是 Node.js 官方提供的包管理工具,用于安装、管理和分享 JavaScript 代码包。安…...

力扣0099——恢复二叉搜索树
恢复二叉搜索树 难度:中等 题目描述 给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。 示例1 输入: root [1,3,null,null,2] 输出:[3,1,null,nul…...
机器学习核心算法
目录 逻辑回归 算法原理 决策树 决策树算法概述 树的组成 决策树的训练与测试 切分特征 衡量标准--熵 信息增益 决策树构造实例 连续值问题解决 预剪枝方法 分类与回归问题解决 决策树解决分类问题步骤 决策树解决回归问题步骤 决策树代码实例 集成算法 Baggi…...

libjsoncpp 的编译和交叉编译
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

【Unity美术】如何用3DsMax做一个水桶模型
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

如何用一根网线和51单片机做简单门禁[带破解器]
仓库:https://github.com/MartinxMax/Simple_Door 支持原创是您给我的最大动力… 原理 -基础设备代码程序- -Arduino爆破器程序 or 51爆破器程序- 任意选一个都可以用… —Arduino带TFT屏幕——— —51带LCD1602——— 基础设备的最大密码长度是0x7F,因为有一位…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
