排序(插入排序)
现在,我们学习了之前数据结构的部分内容,即将进入一个重要的领域:排序,这是一个看起来简单,但是想要理清其中逻辑并不简单的内容,让我们一起加油把!
排序的概念及其运用
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
排序运用
-
商品排序
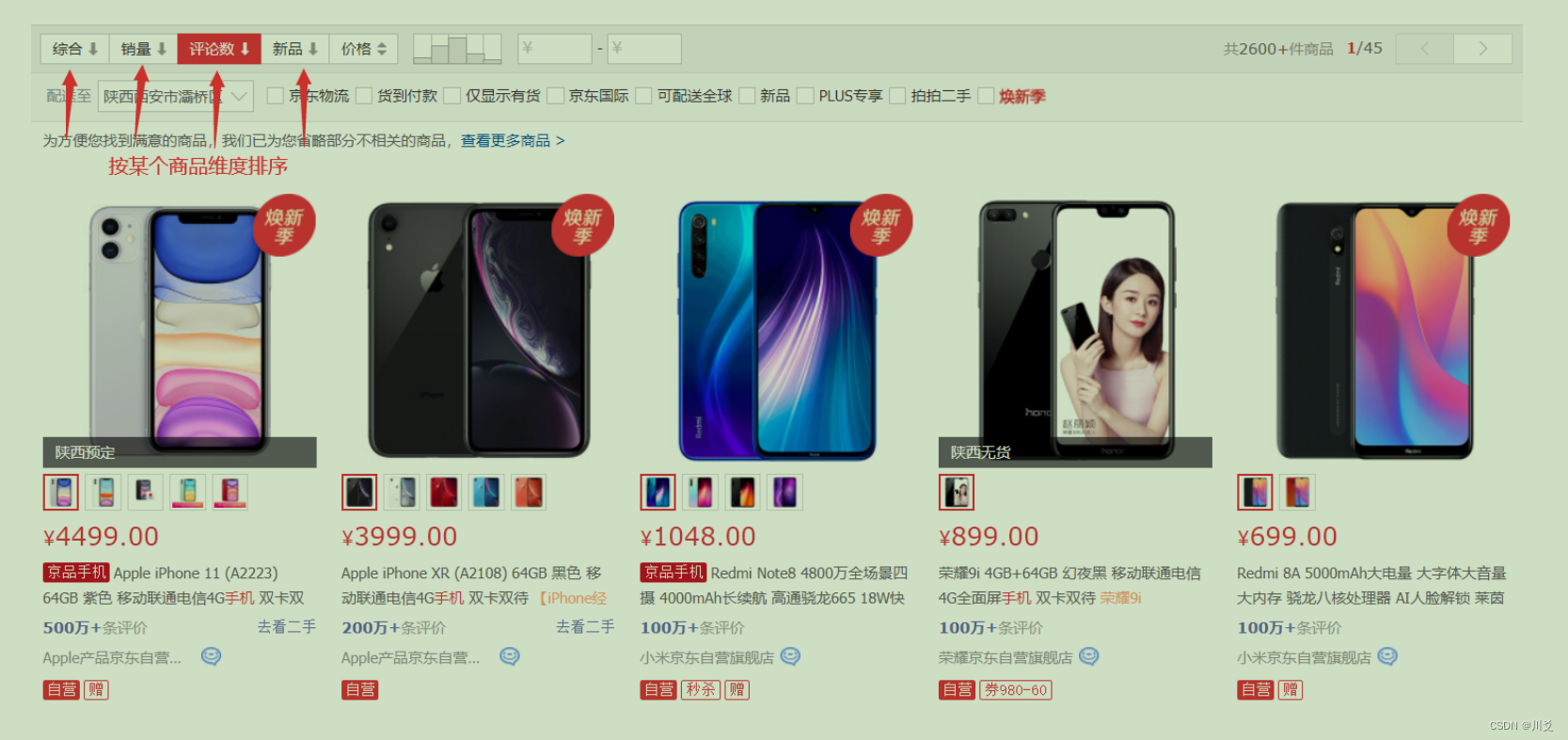
-
院校排名
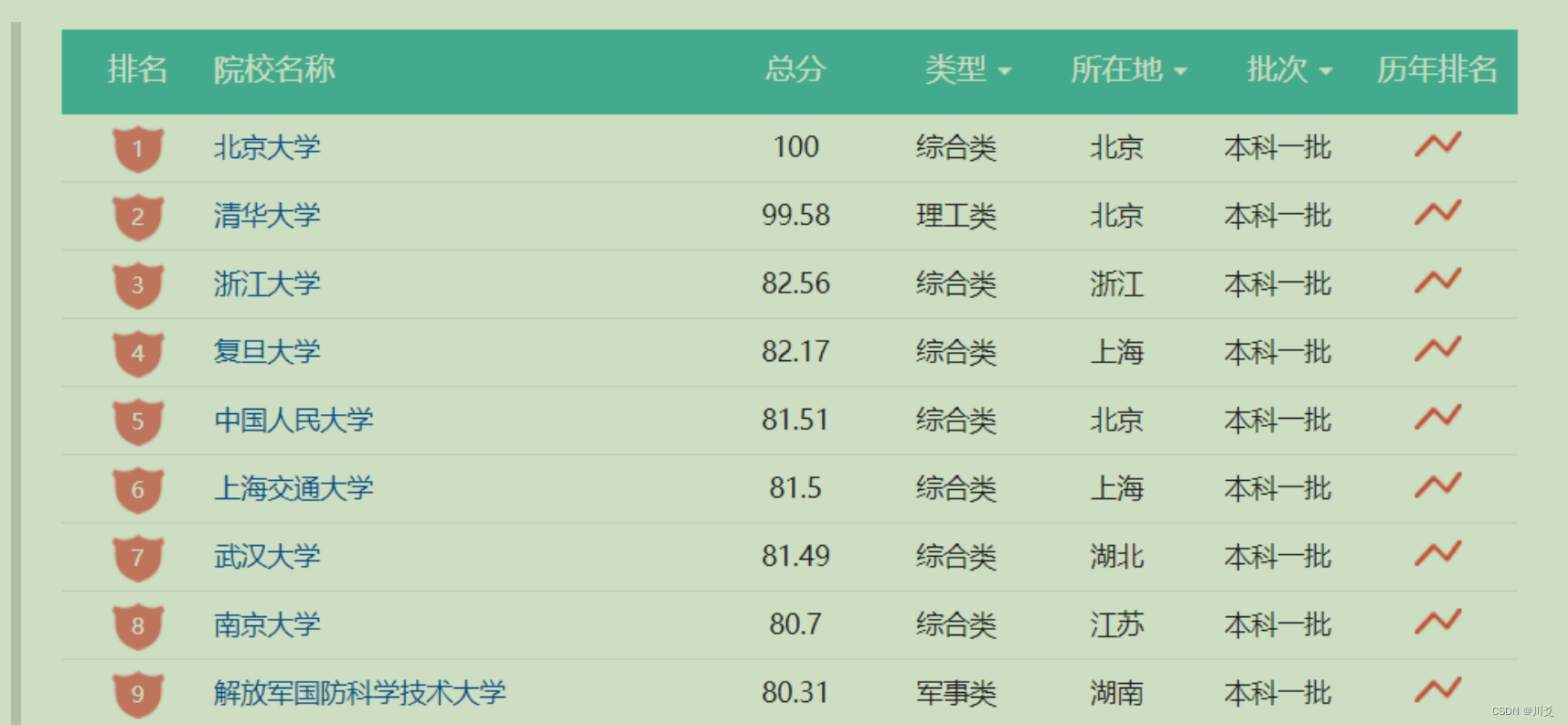
除了这些还有其他的一些地方也会用到排序,总之,我们的生活中处处都存在着排序,所以,学习好排序的使用,对于我们后续学习是十分重要的
常见排序算法
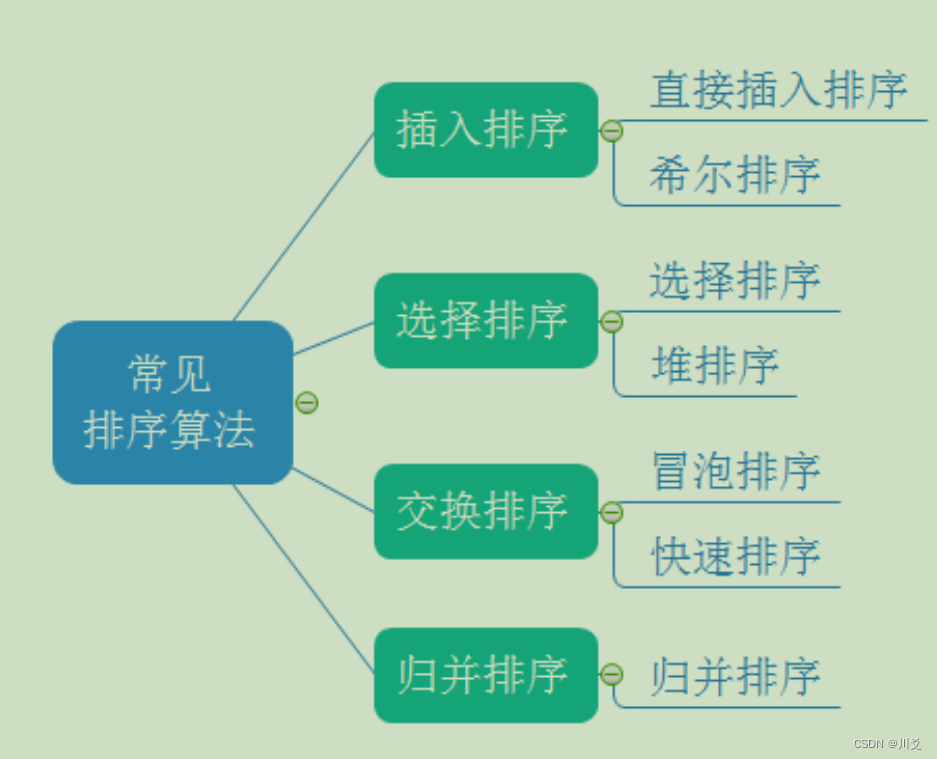
而我们今天讲的重点就是插入排序:其中包含着的就是直接插入排序和希尔排序,而希尔排序事实上就是直接插入排序的升级版
插入排序
基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
直接插入排序
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
我们首先给一个例子为大家讲解一下其中的原理:
int a[ ]={6 9 1 2 5};
假设此时我们要排序的是1,那么我们用end+1作为插入排序元素的下标,end则是前面已经排好顺序的一段,范围为[0,end]。此时我们用一个变量记录住1的值,然后往前比对。我们发现,1比9小,所以end+1下标的位置变为9,然后end–;1比6小,6又被赋值到了原本9的位置上;最后再把1赋值到下标0的位置上,一次排序就成功了。
写成代码是这个样子的:
int end;
int tmp=a[end+1];
while(end>=0){if(tmp<a[end]){a[end+1]=a[end];end--;}else{break;}
}a[end+1]=tmp;
为什么while循环的结束条件是end>=0呢,拿上面的举例,一开始end+1的下标为2,也就是end为1,end- -之后变成了0,而第二次end- -之后直接变成了-1,退出循环。此时end+1=0,也就是数组的第一个元素,最小的元素,刚好就是1
但很明显,这样的话这个函数只能比较一次,怎么样才可以实现多次比较呢,这个时候就需要在外面嵌套一个for循环,然后从0开始一个一个比对,直到n-2(如果是n-1,end+1就是n,就超过数组的下标了,会越界)
所以最终的直接插入排序是这样写的:
//插入排序:前一段有序,在后方插入一个并再次排序
//[0,end] end+1大概就这个意思
//时间复杂度:O(N^2)
//最好的情况:O(N),就算有序也得遍历一遍
void InsertSort(int* a,int n) {for (int i = 0; i < n - 1; i++) {int end = i;int tmp = a[end + 1];while (end >= 0) {if (tmp < a[end]) {a[end + 1] = a[end];end--;}else {break;//终止循环}}a[end + 1] = tmp;}
}
希尔排序(缩小增量排序)
希尔排序(Shell’s Sort)是插入排序的一种更高效的改进版本,也称为缩小增量排序。它的基本思想是:先将整个待排序的记录序列分割成为若干子序列(由相隔某个“增量”的记录组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
希尔排序的增量序列的选择是一个数学难题,通常选取这个常用的增量序列:t1=n/2,ti=ti-1/2,直到ti=1为止。其中,n为待排序序列的长度。按照增量序列的个数k,对序列进行k趟排序。每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m的子序列,分别对各子表进行直接插入排序。仅增量因子为1时,整个序列作为一个表来处理,表长度即为整个序列的长度。
只看概念会觉得晦涩难懂,还是先给大家举一个例子看看:

假设有这么一个数组,我们要对其进行希尔排序,通常会分成两个步骤:
1.预排序:首先将其分为几个组,然后针对每个分组进行插入排序
2.预排序之后,此时数据已经趋于有序,我们再对其整体进行直接插入排序
在这里的话,我们假设间隔3个为一组,那么9,6,3,0就是一组,8,5,2是一组,7,4,1是一组,而我们对每个组进行插入排序之后,顺序就分别变成:0,3,6,9;2,5,8;1,4,7;而放在整体中的话,就是0 2 1 3 5 4 6 8 7 9,可以看出,次序比起一开始的逆序已经好了很多,如果将这一次排序写成代码,就是这个样子的:
int gap=3;//j<n-gap是因为防止越界//内层的for循环只可以提供一组的排序,而外部for循环使每一个组都排序//i=0,i=1,i=2,三个组都可以排序for(int i=0;i<gap;i++){for(int j=i;j<n-gap;j+=gap){int end=j;int tmp=a[end+gap];while(end>=0){if(tmp<a[end]){a[end+gap]=a[end];end-=gap;}else{break;}} a[end+gap]=tmp;}}
但是很明显,这样子的话,只比较排序了一次,但我们需要的是在保证最后一次比较是gap==1的情况下,前面的预排序也要到位。但首先我们先把预排序的函数再修改一下,让它不用分组排序,而是多组并排。
int gap=3;
for(int i=0;i<n-gap;i++){int end=i;int tmp=a[end+gap];while(end>=0){if(tmp<a[end]){a[end+gap]=a[end];end-=gap;}else{break;}}a[end+gap]=tmp;
}
这样子的话,就不是一个一个组的排,而是从第一个元素开始,按照其组别来排顺序,相对于分组比较,多组并排明显更简洁
完成这些之后,我们就可以着手开始实现真正的希尔排序了!
void ShellSort(int* a,int n){int gap=n;//gap>1时是预排序,目的:接近有序//gap==1时就是直接插入排序,目的:有序while(gap>1){gap=gap/2;//让其预排序之后最终gap==1,进行最终的直接插入排序//gap越大,大的值更快调到后面,小的值可以更快的调到前面,越不接近有序;gap越小,跳得越慢,但是越接近有序。//gap=gap/3+1;也可以,效率更高,时间复杂度更低,一个是log2N,一个是log3Nfor(int i=0;i<n-gap;i++){int end=i;int tmp=a[end+gap];while(end>=0){if(tmp<a[end]){a[end+tmp]=a[end];end-=gap;}else{break;}}a[end+gap]=tmp;}}
那么大家一定很好奇,这么复杂的希尔排序,它的时间复杂度相较直接插入排序相比是否有进步,它的使用效率是否高于直接插入排序,接下来我就为大家来展示一下它们的差别。
int main() {int size = 10000;int arr[10000];// 使用时间种子初始化伪随机数生成器srand(time(0));// 填充数组for (int i = 0; i < size; i++) {arr[i] = rand() % 1000; // 生成0到999之间的随机数}clock_t start, end;double cpu_time_used;// 测试插入排序的执行时间start = clock();InsertSort(arr, size);end = clock();cpu_time_used = ((double)(end - start)) / CLOCKS_PER_SEC;printf("InsertSort took %f seconds to execute \n", cpu_time_used);// 测试希尔排序的执行时间start = clock();ShellSort(arr, size);end = clock();cpu_time_used = ((double)(end - start)) / CLOCKS_PER_SEC;printf("ShellSort took %f seconds to execute \n", cpu_time_used);return 0;
}

可以看出,在初始化10000个随机数的数组中,直接插入排序和希尔排序之间的效率差了几十倍,而如果数据更多,可能差的还会更多。
在最坏情况下(完全逆序),希尔排序的时间复杂度是O(n^2),这与直接插入排序的时间复杂度相同,但是在一般情况下其平均时间复杂度要优于O(n ^2)。希尔排序时间复杂度的优劣程度取决于间隔序列的选取,不同的间隔序列的希尔排序的时间复杂度也会有所不同。
在实际使用中,通常使用增量序列为n/2,k=k/2,…1的希尔排序,在平均情况下,其时间复杂度大约介于O(n^1.3)和O(n ^2)之间,这使得希尔排序在中等规模数据时具有较好的性能。
其实我们自己也可以简单分析一下,以最坏情况来看:
gap很大时,gap==n/3+1,此时我们忽略+1 。这一趟每组3个,移动次数:第二个最多移动1次,第三个最多移动2次,合计为3;而总计有3/n组,累计移动的次数是(1+2) * 3/n=n
而下一轮预排序,gap==n/9,每组9个,移动次数:1+2+3…+8=36;总计n/9组,累计移动次数4n,但这是最坏的情况下做出的判断,在经历过第一次排序之后,已经比刚才更接近有序,不会所有的元素都要排序,所以次数必定是小于4n的,而后面的预排序也是与这个一样的,所以我们并不确定其时间复杂度,只能算出一个大概的区间,具体情况只能跟当前排序的数据元素相关,需要经过大量分析才能得出结论。
以上就是排序的第一讲:插入排序!下一节我们将会讲解选择排序,欢迎大家关注后续文章!
相关文章:

排序(插入排序)
现在,我们学习了之前数据结构的部分内容,即将进入一个重要的领域:排序,这是一个看起来简单,但是想要理清其中逻辑并不简单的内容,让我们一起加油把! 排序的概念及其运用 排序的概念 排序&…...
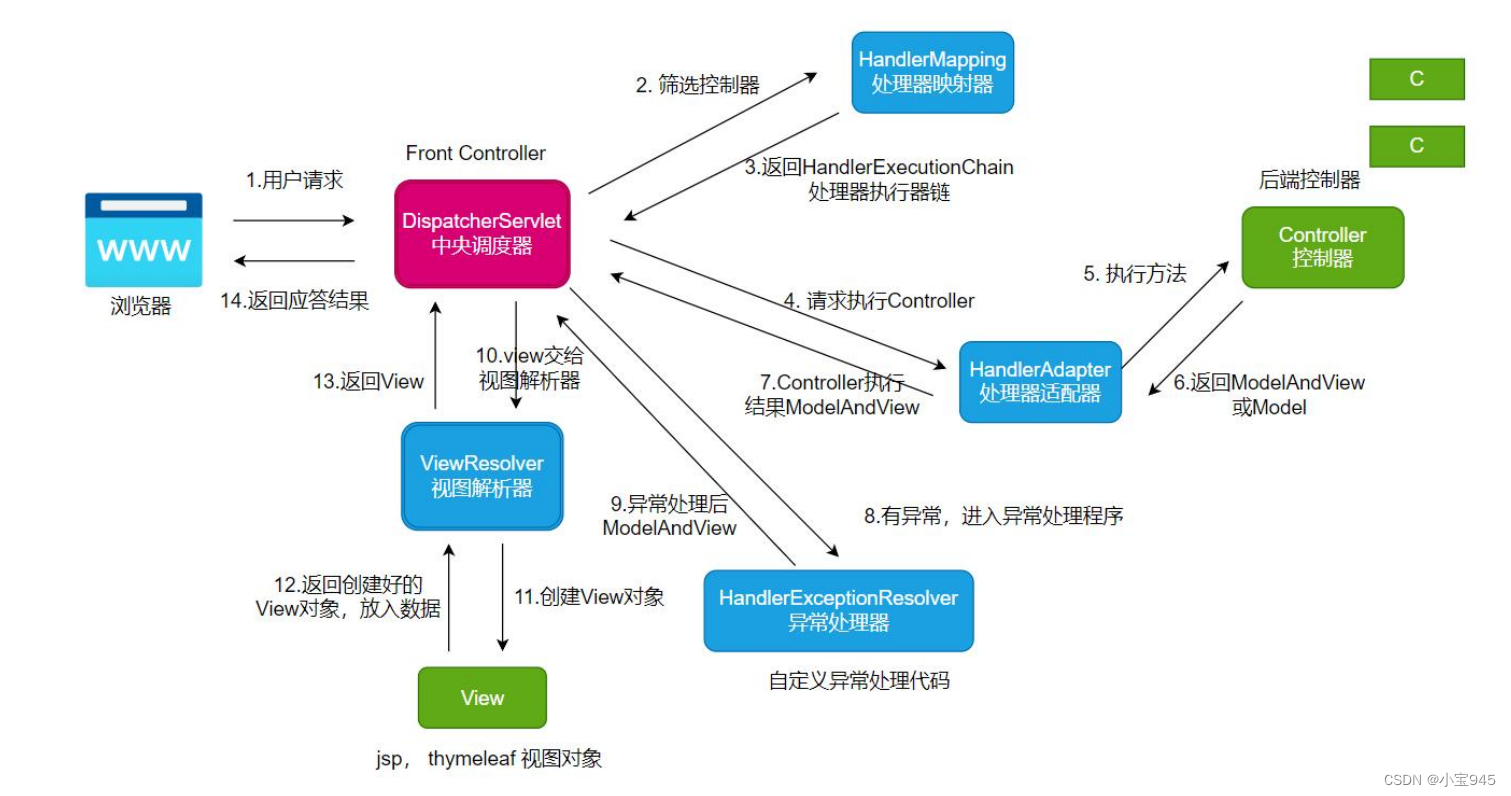
Spring MVC 请求流程
SpringMVC 请求流程 一、DispatcherServlet 是一个 Servlet二、Spring MVC 的完整请求流程 Spring MVC 框架是基于 Servlet 技术的。以请求为驱动,围绕 Servlet 设计的。Spring MVC 处理用户请求与访问一个 Servlet 是类似的,请求发送给 Servlet…...
鸿蒙ArkUI 宫格+列表+HttpAPI实现
鸿蒙ArkUI学习实现一个轮播图、一个九宫格、一个图文列表。然后请求第三方HTTPAPI加载数据,使用了axios鸿蒙扩展库来实现第三方API数据加载并动态显示数据。 import {navigateTo } from ../common/Pageimport axios, {AxiosResponse } from ohos/axiosinterface IDa…...
【C++中的STL】常用算法1——遍历算法和查找算法
常用算法1 常用算法常用遍历算法for_eachtransform 常用查找算法findfind_ifadjacent_findbinary_searchcountcount_if 常用算法 算法主要是由头文件<algorithm><functional><numeric>组成。 <algorithm>是所有STL头文件中最大的一个,范围…...
Jmeter性能测试: 基于JDK 21 安装 Jmeter 5.6.3
目录 一、实验 1.环境 2.JDK下载 3.Jmeter下载 4.Windows安装JDK 21 5.Windows安装Jmeter 5.6.3 6.Linux安装JDK 21 7.Linux安装Jmeter 5.6.3 二、问题 1. Linux 的profile、bashrc、bash_profile文件有哪些区别 一、实验 1.环境 (1)主机 表…...
)
Linux命令-apropos命令(在 whatis 数据库中查找字符串)
补充说明 apropos命令 在一些特定的包含系统命令的简短描述的数据库文件里查找关键字,然后把结果送到标 准输出。 如果你不知道完成某个特定任务所需要命令的名称,可以使用一个关键字通过Linux apropos实用程 序来搜索它。该实用程序可以搜索关键字并且…...

【算法】解决动态规划问题的通用步骤思路及示例算法:打家劫舍【动态规划】
动态规划(Dynamic Programming,简称DP)是一种解决问题的算法设计技术,通常用于优化问题。它通过将问题分解为更小的子问题,并解决这些子问题,然后合并它们的解决方案来解决原始问题。动态规划通常用于具有重叠子问题和最优子结构性质的问题。 动态规划的主要思想是避免重…...

蓝桥杯之即约分数
求1~N的所有即约分数 公约数求法:可以使用欧几里得除法求得公约数 算法原理: a,b为两个整数,a>b a除以b的商q1和余数r1 如果r1为0,则最大公约数就为b 如果不为0,则继续使用b除以r取商为q2,余r2 如果r2为0࿰…...

Pointnet++改进优化器系列:全网首发Sophia优化器 |即插即用,实现有效涨点
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入Sophia优化器,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3...
)
1.27回溯(中等)
1.全排列 全排列 II 1.给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 2.给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,2,3…...
sql管理工具archery简介
在平时的工作过程中,我们肯定会遇到使用sql平台的场景,业内也有很多工具,类似阿里云的dms,但是这个是和云厂商绑定的,我们可能一般没有用到阿里云组件就比较困难了,那还有什么选项了,经过调研&a…...

DEM高程地形瓦片数据Cesium使用教程
一、简介 从开始写文章到现在,陆续发布了全球90m、30m(包括哥白尼及ALOS)、12.5m全球级瓦片数据,以及中国12.5、日本10m、新西兰8m、等国家级瓦片数据,同时也发布了台湾20m、中国34省区12.5m等地区级瓦片数据。在数据发布的文章中对数据如何…...
3个精美的wordpress律师网站模板
暗红色WordPress律师事务所网站模板 演示 https://www.zhanyes.com/qiye/23.html 暗橙色WordPress律师网站模板 演示 https://www.zhanyes.com/qiye/18.html 红色WordPress律所网站模板 演示 https://www.zhanyes.com/qiye/22.html...
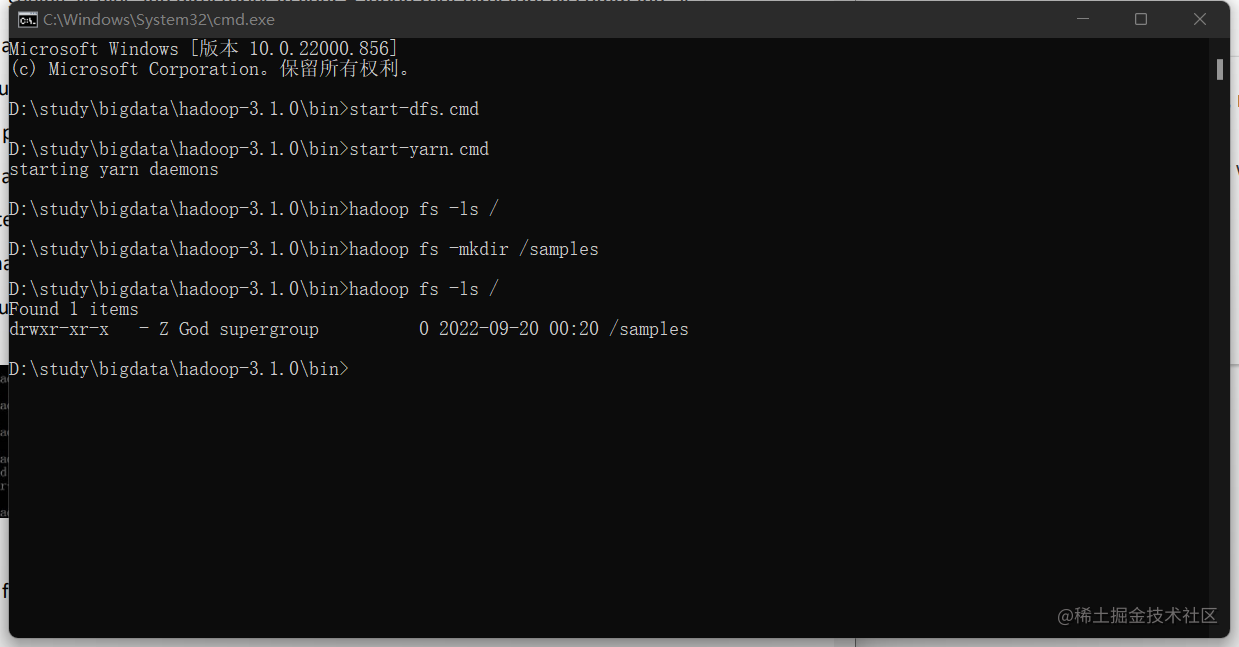
在windows环境下安装hadoop
Hadoop是一个分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。但这个架构是基于java语言开发的,所以要先进行jdk的安装,如果电脑已经配置过jdk或者是曾经运行成功过java文件,那就可以跳过第一步。 …...

大数据分析组件Hive-集合数据结构
Hive的数据结构 前言一、array数组类型二、map键值对集合类型三、struct结构体类型 前言 Hive是一个基于Hadoop的数据仓库基础设施,用于处理大规模分布式数据集。它提供了一个类似于SQL的查询语言(称为HiveQL),允许用户以类似于关…...

单核QPS近6000S,陌陌基于OceanBase的持久化缓存探索与实践
挚文集团于 2011 年 8 月推出了陌陌,这款立足地理位置服务的开放式移动视频社交应用在中国社交平台领域内独树一帜。陌陌和探探作为陌生人社交领域的主流应用,涵盖了多种核心业务模块,包括直播服务、附近动态功能、即时通讯(IM&am…...

关于css 的基础试题
CSS是什么的缩写? A. Creative Style SheetsB. Cascading Style SheetsC. Computer Style SheetsD. Colorful Style Sheets 在HTML中,通过什么标签引入CSS样式? A. <script>B. <style>C. <link>D. <css> 以下哪个选项…...

Keil-C语言小总结
1、 &取地址符,*取地址内容 int *ptr;//声明指针 2、ptr &c; // 将c的地址赋值给指针变量ptr 3、可选参数函数 4、C宏定义 5、 memset:最快的数据清零函数 void *memset(void *s, int ch, size_t n); 分别是 字符串 要值的数据(0…...

react的withRouter高阶组件:
withRouter的作用就是, 如果我们某个东西不是一个Router, 但是我们要依靠它去跳转一个页面, 比如点击页面的logo, 返回首页, 这时候就可以使用withRouter来做. 在 React Router 中,withRouter 是一个函数,用于与路由相关的组件。它接受一个组件作为参数&…...

小程序 样式 WXSS
文章目录 样式 WXSS尺⼨单位样式导⼊选择器⼩程序中使⽤less 样式 WXSS WXSS( WeiXin Style Sheets )是⼀套样式语⾔,⽤于描述 WXML 的组件样式。 与 CSS 相⽐,WXSS 扩展的特性有: 响应式⻓度单位 rpx样式导⼊ 尺⼨单位 rpx (…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
