蓝桥杯之即约分数
求1~N的所有即约分数
公约数求法:可以使用欧几里得除法求得公约数
算法原理:
a,b为两个整数,a>b
a除以b的商q1和余数r1
如果r1为0,则最大公约数就为b
如果不为0,则继续使用b除以r取商为q2,余r2
如果r2为0,则最大公约数是r1,
如果不为0,则继续使用r2除以r1
递归思想,始终是上一次的除数除以上一次的余数,然后判断是否本次余数为0否,为0,则返回除数
gcd(a,b)
return gcd(b,a%b);
当然,递归要加终止条件
完整版
int gcd(int a,int b )
{
if (b==0) return a;return gcd(b,a%b);
}
最终代码:
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b);
signed main()
{int ans=0;for(int i=1;i<=2020;i++) {for(int j=1;j<=i;j++)//if(__gcd(i,j)==1) ans++;if(gcd(i,j)==1) ans++;}cout<<2*ans-1<<endl;return 0;}
int gcd(int a,int b )
{
if (b==0) return a;return gcd(b,a%b);
}这里,最小公倍数就也很好计算了,
两个数相乘,除以最大公约数就是最小公倍数
改进算法
求即约分数,即要求分子与分母互质,互为质数。根据数论知识,1~n中与n互质的数的个数称为欧拉函数,记作phi[n]。
唯一分解定理,任何一个数,要么本身是质数,要么可以分解为有限个质数的乘积。
根据欧拉公式和唯一分解定理,可得算法如下:
唯一分解定理```cpp
//唯一分解定理,能够把任意一个数分解成有限个质数的相乘
int getPrime(int p[],int n)
{int k=0;//记录质数的个数for(int i=2;i*i<=n;i++){if(n%i==0) p[++k]=i;//如果能够被除掉,说明i就是其一个质数while(n%i==0) n/=i;//等同于n=n/i,出去其重复因子}if(n>1) p[++k]=n;//前面没有一个数满足要求,则这个数质数因子只有是n本身了return k;
}
```求Euler函数
```cpp
//求解欧拉函数
int getEuler(int n)
{int phi=n;int k=getPrime(P,n);for(int i=1;i<=k;i++){phi=phi-phi/P[i];}return phi;
}
```全部代码如下:
#include<bits/stdc++.h>
using namespace std;
int P[2020]={0};
//唯一分解定理,能够把任意一个数分解成有限个质数的相乘
int getPrime(int p[],int n)
{int k=0;//记录质数的个数for(int i=2;i*i<=n;i++){if(n%i==0) p[++k]=i;//如果能够被除掉,说明i就是其一个质数while(n%i==0) n/=i;//等同于n=n/i,出去其重复因子}if(n>1) p[++k]=n;//前面没有一个数满足要求,则这个数质数因子只有是n本身了return k;
}
//求解欧拉函数
int getEuler(int n)
{int phi=n;int k=getPrime(P,n);for(int i=1;i<=k;i++){phi=phi-phi/P[i];}return phi;
}int main()
{int ans=0;int ans1=0;ans=getPrime(P,2020); for(int i=1;i<=2020;i++)ans1+=getEuler(i);cout<<2*ans1-1<<endl;return 0;
}

相关文章:

蓝桥杯之即约分数
求1~N的所有即约分数 公约数求法:可以使用欧几里得除法求得公约数 算法原理: a,b为两个整数,a>b a除以b的商q1和余数r1 如果r1为0,则最大公约数就为b 如果不为0,则继续使用b除以r取商为q2,余r2 如果r2为0࿰…...

Pointnet++改进优化器系列:全网首发Sophia优化器 |即插即用,实现有效涨点
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入Sophia优化器,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3...
)
1.27回溯(中等)
1.全排列 全排列 II 1.给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 2.给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输入:nums [1,2,3…...
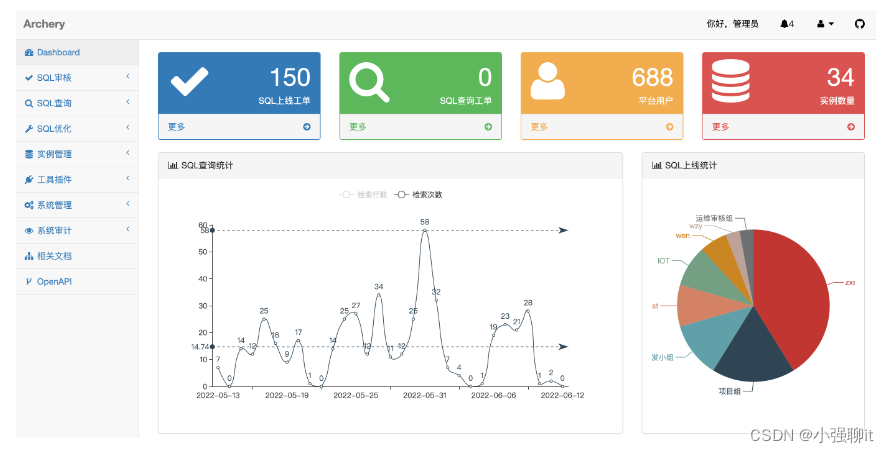
sql管理工具archery简介
在平时的工作过程中,我们肯定会遇到使用sql平台的场景,业内也有很多工具,类似阿里云的dms,但是这个是和云厂商绑定的,我们可能一般没有用到阿里云组件就比较困难了,那还有什么选项了,经过调研&a…...

DEM高程地形瓦片数据Cesium使用教程
一、简介 从开始写文章到现在,陆续发布了全球90m、30m(包括哥白尼及ALOS)、12.5m全球级瓦片数据,以及中国12.5、日本10m、新西兰8m、等国家级瓦片数据,同时也发布了台湾20m、中国34省区12.5m等地区级瓦片数据。在数据发布的文章中对数据如何…...
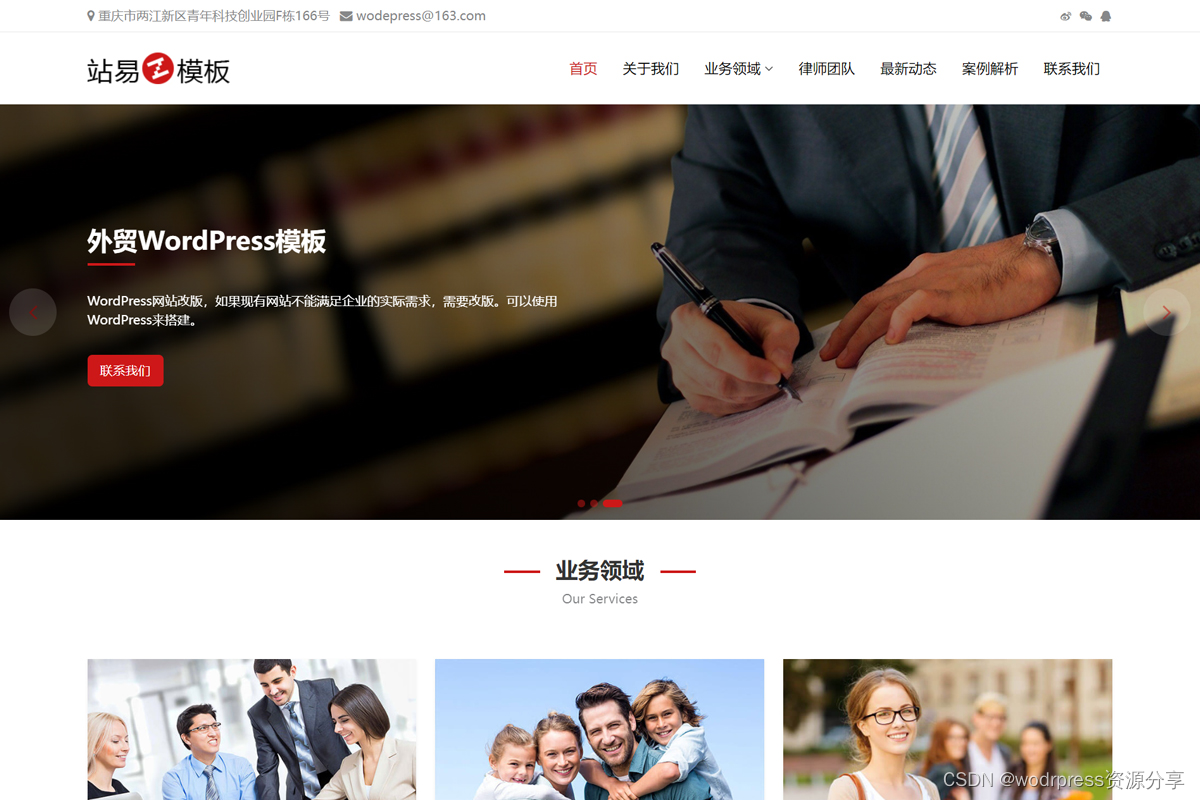
3个精美的wordpress律师网站模板
暗红色WordPress律师事务所网站模板 演示 https://www.zhanyes.com/qiye/23.html 暗橙色WordPress律师网站模板 演示 https://www.zhanyes.com/qiye/18.html 红色WordPress律所网站模板 演示 https://www.zhanyes.com/qiye/22.html...
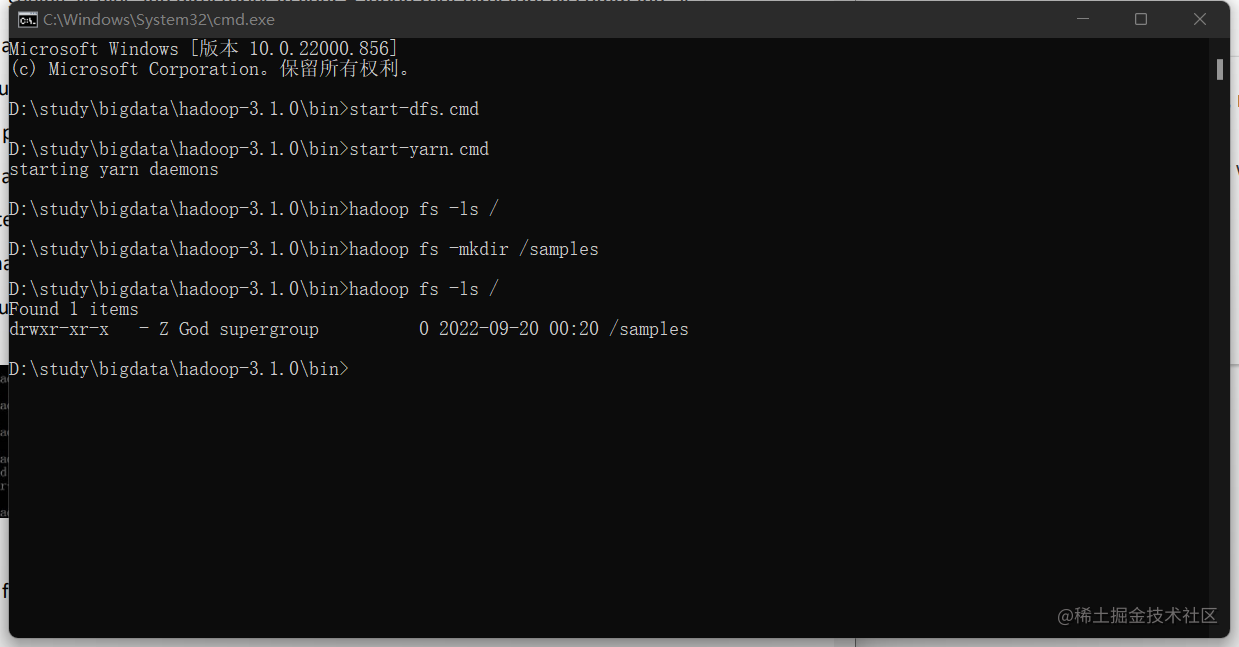
在windows环境下安装hadoop
Hadoop是一个分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。但这个架构是基于java语言开发的,所以要先进行jdk的安装,如果电脑已经配置过jdk或者是曾经运行成功过java文件,那就可以跳过第一步。 …...

大数据分析组件Hive-集合数据结构
Hive的数据结构 前言一、array数组类型二、map键值对集合类型三、struct结构体类型 前言 Hive是一个基于Hadoop的数据仓库基础设施,用于处理大规模分布式数据集。它提供了一个类似于SQL的查询语言(称为HiveQL),允许用户以类似于关…...

单核QPS近6000S,陌陌基于OceanBase的持久化缓存探索与实践
挚文集团于 2011 年 8 月推出了陌陌,这款立足地理位置服务的开放式移动视频社交应用在中国社交平台领域内独树一帜。陌陌和探探作为陌生人社交领域的主流应用,涵盖了多种核心业务模块,包括直播服务、附近动态功能、即时通讯(IM&am…...

关于css 的基础试题
CSS是什么的缩写? A. Creative Style SheetsB. Cascading Style SheetsC. Computer Style SheetsD. Colorful Style Sheets 在HTML中,通过什么标签引入CSS样式? A. <script>B. <style>C. <link>D. <css> 以下哪个选项…...

Keil-C语言小总结
1、 &取地址符,*取地址内容 int *ptr;//声明指针 2、ptr &c; // 将c的地址赋值给指针变量ptr 3、可选参数函数 4、C宏定义 5、 memset:最快的数据清零函数 void *memset(void *s, int ch, size_t n); 分别是 字符串 要值的数据(0…...

react的withRouter高阶组件:
withRouter的作用就是, 如果我们某个东西不是一个Router, 但是我们要依靠它去跳转一个页面, 比如点击页面的logo, 返回首页, 这时候就可以使用withRouter来做. 在 React Router 中,withRouter 是一个函数,用于与路由相关的组件。它接受一个组件作为参数&…...

小程序 样式 WXSS
文章目录 样式 WXSS尺⼨单位样式导⼊选择器⼩程序中使⽤less 样式 WXSS WXSS( WeiXin Style Sheets )是⼀套样式语⾔,⽤于描述 WXML 的组件样式。 与 CSS 相⽐,WXSS 扩展的特性有: 响应式⻓度单位 rpx样式导⼊ 尺⼨单位 rpx (…...
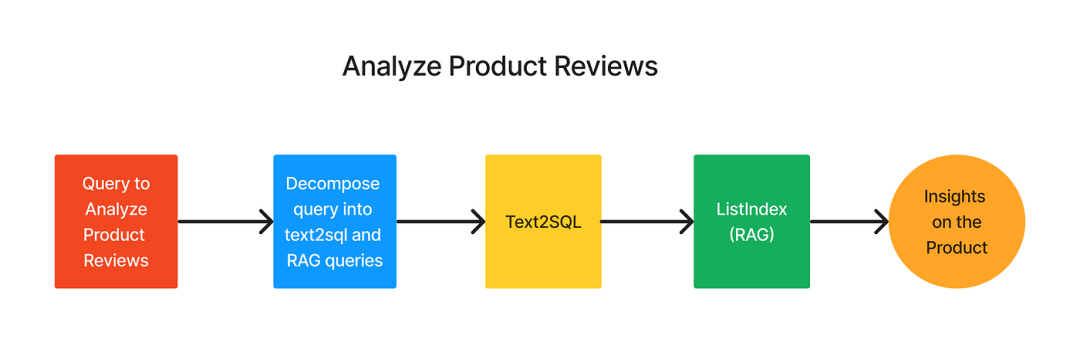
LLM之RAG实战(二十一)| 使用LlamaIndex的Text2SQL和RAG的功能分析产品评论
亚马逊和沃尔玛等电子商务平台上每天都有大量的产品评论,这些评论是反映消费者对产品情绪的关键接触点。但是,企业如何从庞大的数据库获得有意义的见解? 我们可以使用LlamaIndex将SQL与RAG(Retrieval Augmented Generation&#x…...
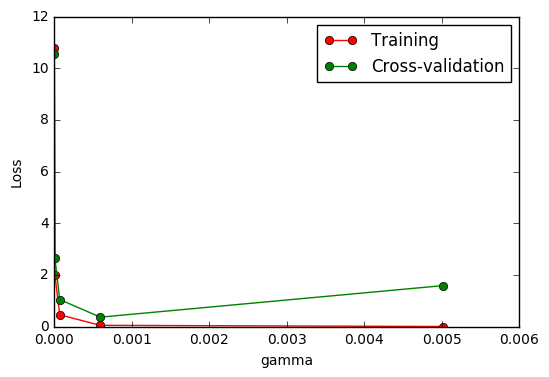
Scikit-learn (sklearn)速通 -【莫凡Python学习笔记】
视频教程链接:【莫烦Python】Scikit-learn (sklearn) 优雅地学会机器学习 视频教程代码 scikit-learn官网 莫烦官网学习链接 本人matplotlib、numpy、pandas笔记 1 为什么学习 Scikit learn 也简称 sklearn, 是机器学习领域当中最知名的 python 模块之一. Sk…...

支持向量机(SVM)详解
支持向量机(support vector machines,SVM)是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机。 1、线性可分支持向量机与硬间隔最大化 1.1、线性可分支持向量机 考虑一个二分…...

huggingface学习|云服务器部署Grounded-Segment-Anything:bug总会一个一个一个一个又一个的解决的
文章目录 一、环境部署(一)模型下载(二)环境配置(三)库的安装 二、运行(一) 运行grounding_dino_demo.py文件(二)运行grounded_sam_demo.py文件(三…...

【最佳实践】Go 组合模式对业务解耦
在 Go 语言中,组合模式(Composition)是通过嵌入结构体(embedding structs)来实现的。它允许我们构建复杂的对象,通过将简单对象组合成树形结构来表示整个部分的层次结构。在 Go 中,这种模式不仅…...

arm 汇编调用C
arm64 汇编调用C函数 main.s .section .text .globl main main:stp x29, x30, [sp, -16]! //store fp x29 lr x30mov x0, #0mov x1, #1bl addmov x1, x0 // x0 return ldp x29, x30, [sp], 16 //restore fp lrretadd.c #include <stdio.h> int add(int a, int…...
Vue3+Vite使用Puppeteer进行SEO优化(SSR+Meta)
1. 背景 【笑小枫】https://www.xiaoxiaofeng.com上线啦 资源持续整合中,程序员必备网站,快点前往围观吧~ 我的个人博客【笑小枫】又一次版本大升级,虽然知道没有多少访问量,但我还是整天没事瞎折腾。因为一些功能在Halo上不太好实…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
