【数据结构】邻接矩阵和邻接图的遍历

写在前面
本篇文章开始学习数据结构的图的相关知识,涉及的基本概念还是很多的。
本文的行文思路:
学习图的基本概念
学习图的存储结构——本文主要介绍邻接矩阵和邻接表
对每种结构进行深度优先遍历和广度优先遍历
先识概念
话不多说,狠活献上
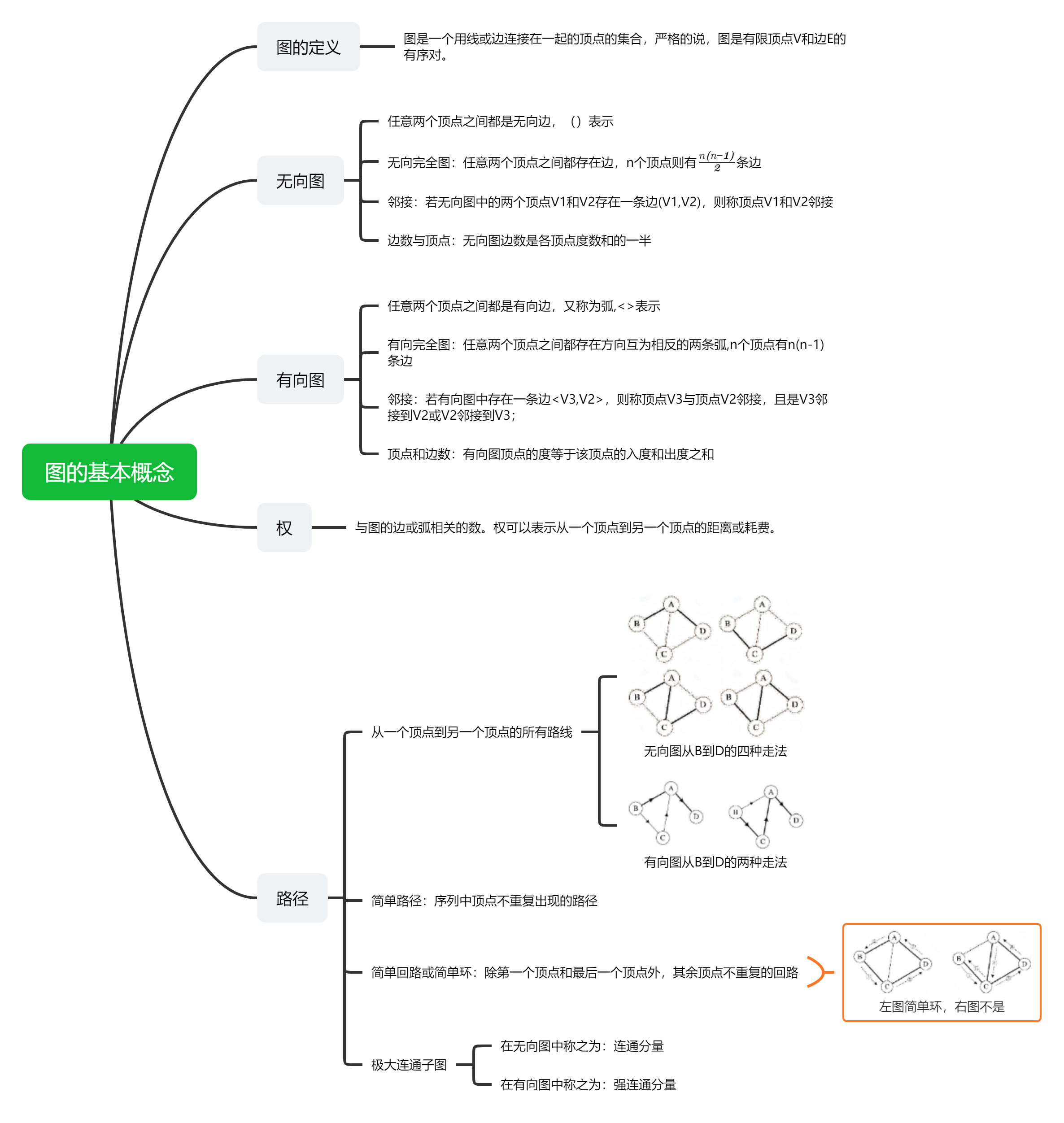
学习思想
等等,先别急,正式学习之前先认识几个英语单词及缩写
类型(Type)
顶点(vertex)
边(Edge)
邻接(adjacency,简写adj)
邻接矩阵(adjacency Matrix)
邻接表(adjacency List)
深度优先遍历(Depth First Search,简称BFS)
广度优先遍历(Breadth First Search,简称DFS)
邻接矩阵的存储结构
typedef char VertexType; //顶点类型
typedef int EdgeType; //边类型
#define MAXVEX 100 //最大顶点数目
#define INFINITY 65535 //用65535表示无穷//邻接矩阵的存储结构typedef struct
{VertexType vexs[MAXVEX]; //顶点数组EdgeType arc[MAXVEX][MAXVEX]; //边数组int numVertexes, numEdges; //当前顶点的顶点数和边数
}MGraph;邻接表的存储结构
#define MAXVEX 100
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上的权值类型int visited[MAXVEX];typedef struct EdgeNode //边表结点
{int adjvex; //存储该顶点对应的下标EdgeType info; //存储权值,非网图则无需struct EdgeNode* next;
}EdgeNode;typedef struct VertexNode //顶点结点
{VertexType data; //存储顶点信息EdgeNode* firstedge; //边表头指针
}VertexNode, AdjList[MAXVEX];//邻接表存储结构typedef struct
{AdjList adjList;int numVertexes, numEdges; //当前顶点数目和边数
}GraphAdjList;再学应用
邻接矩阵的深度遍历和广度遍历
深度遍历:实际上就是二叉树的前序遍历
广度遍历:实际上就是二叉树的层序遍历,要用到队列,我们自己还要写出队列的一些基本操作
#include<stdio.h>
#include<malloc.h>typedef char VertexType; //顶点类型
typedef int EdgeType; //边类型
#define MAXVEX 100 //最大顶点数目
#define INFINITY 65535 //用65535表示无穷//邻接矩阵的存储结构typedef struct
{VertexType vexs[MAXVEX]; //顶点数组EdgeType arc[MAXVEX][MAXVEX]; //边数组int numVertexes, numEdges; //当前顶点的顶点数和边数
}MGraph;//邻接矩阵的初始化void CreateMGraph(MGraph* G)
{int i, j, k;printf("请输入顶点的个数和边数:");scanf("%d%d", &G->numVertexes, &G->numEdges);for (i = 0; i < G->numVertexes; i++){printf("请输入%d个顶点: ", i + 1);scanf("%s", &G->vexs[i]);}//将矩阵的所有数据初始化为"无穷"for (i = 0; i < G->numVertexes; i++)for (j = 0; j < G->numVertexes; j++)G->arc[i][j] = INFINITY;//然后自定义矩阵中的数据for (k = 0; k < G->numEdges; k++){printf("请输入边(vi,vj)中的下标i和j: ");scanf("%d%d", &i, &j);G->arc[i][j] = 1;G->arc[j][i] = G->arc[i][j]; //无向图的邻接矩阵沿着右对角线对称}
}int visited[MAXVEX]; //访问标志的数组//深度优先递归算法void DFS(MGraph G, int i)
{int j;visited[i] = 1; //将第i个顶点标记为已访问printf("%c ", G.vexs[i]); //打印顶点,也可以是其他操作//循环遍历G中所有的顶点for (j = 0; j < G.numVertexes; j++){//判断当前正在遍历的顶点j和顶点i是否相邻且未被访问过,相连为1,不相连为0(前提是不带权的图)if (G.arc[i][j] == 1 && !visited[j]) DFS(G, j);}}//邻接矩阵的深度遍历操作void DFSTraverse(MGraph G)
{int i;//初始化所有顶点状态都是未访问过的 for (i = 0; i < G.numVertexes; i++){visited[i] = 0;}//对所有未访问过的顶点调用DFS,若为连通图则只执行一次for (i = 0; i < G.numVertexes; i++){if (!visited[i])DFS(G, i);}
}//队列的顺序存储结构
typedef struct
{char data[MAXVEX];int front;int rear;
}SqQueue;void InitQueue(SqQueue* Q)
{Q->front = 0;Q->rear = 0;
}void EnQueue(SqQueue* Q,int e)
{if ((Q->rear + 1) % MAXVEX == Q->front)return;Q->data[Q->rear] = e;Q->rear = (Q->rear + 1) % MAXVEX;
}void DeQueue(SqQueue* Q, int* e)
{if (Q->front == Q->rear)return;*e = Q->data[Q->front];Q->front = (Q->front + 1) % MAXVEX;}int QueueEmpty(SqQueue Q)
{return Q.front == Q.rear;
}//邻接矩阵的广度遍历void BFSTraverse(MGraph G)
{int i, j;SqQueue Q;for (i = 0; i < G.numVertexes; i++){visited[i] = 0; //将每一个顶点都设置未访问}InitQueue(&Q); //初始化一个辅助用的队列for (i = 0; i < G.numVertexes; i++){if (!visited[i]){visited[i] = 1; //设置当前顶点为已访问printf("%c ", G.vexs[i]);EnQueue(&Q, i); //将此顶点入队列while (!QueueEmpty(Q)){DeQueue(&Q, &i); //首元素出队,赋给ifor (j = 0; j < G.numVertexes; j++){if (G.arc[i][j] == 1 && !visited[j]) //边存在且未被访问过{visited[j] = 1; //设置当前顶点为已访问printf("%c ", G.vexs[j]); //打印顶点EnQueue(&Q, j); //将此顶点入队}}}}}
}int main()
{MGraph G;CreateMGraph(&G);printf("DFS遍历顺序:");DFSTraverse(G);printf("\n");printf("BFS遍历顺序:");BFSTraverse(G);printf("\n");return 0;
}
邻接表的深度遍历和广度遍历
#define _CRT_SECURE_NO_WARNINGS 1
//图的遍历主要有两种,深度优先遍历和广度优先遍历
//深度优先遍历实际上是二叉树的先序遍历,广度优先遍历实际上是二叉树的层序遍历#include<stdio.h>
#include<malloc.h>
#define MAXVEX 100
typedef char VertexType; //顶点类型
typedef int EdgeType; //边上的权值类型int visited[MAXVEX];typedef struct EdgeNode //边表结点
{int adjvex; //存储该顶点对应的下标EdgeType info; //存储权值,非网图则无需struct EdgeNode* next;
}EdgeNode;typedef struct VertexNode //顶点结点
{VertexType data; //存储顶点信息EdgeNode* firstedge; //边表头指针
}VertexNode, AdjList[MAXVEX];//邻接表存储结构typedef struct
{AdjList adjList;int numVertexes, numEdges; //当前顶点数目和边数
}GraphAdjList;//邻接表的初始化
void CreateALGraph(GraphAdjList* GL)
{int i, j, k;EdgeNode* e;printf("输入顶点数和边数:");scanf("%d%d", &GL->numVertexes, &GL->numEdges);//将数据存进顶点数组,把顶点指针域置空for (i = 0; i < GL->numVertexes; i++){getchar();printf("请输入第%d个顶点:", i + 1);scanf("%c", &GL->adjList[i].data);GL->adjList[i].firstedge = NULL;}for (k = 0; k < GL->numEdges; k++){printf("输入边(vi,vj)上的顶点序号:");scanf("%d%d", &i, &j);//结点i记录结点j的下标e = (EdgeNode*)malloc(sizeof(EdgeNode));e->adjvex = j;e->next = GL->adjList[i].firstedge; //下面两步相当于链表的头插法GL->adjList[i].firstedge = e;//结点j记录结点i的下标e = (EdgeNode*)malloc(sizeof(EdgeNode));e->adjvex = i;e->next = GL->adjList[j].firstedge; //下面两步相当于链表的头插法GL->adjList[j].firstedge = e;}}//邻接表的深度优先递归算法void DFS(GraphAdjList GL, int i)
{EdgeNode* p;visited[i] = 1;printf("%c ", GL.adjList[i].data);p = GL.adjList[i].firstedge;while (p){if (!visited[p->adjvex])DFS(GL, p->adjvex);p = p->next;}
}//邻接表的深度遍历操作
void DFSTraverse(GraphAdjList GL)
{int i;for (i = 0; i < GL.numVertexes; i++){visited[i] = 0;}for (i = 0; i < GL.numVertexes; i++){if (!visited[i])DFS(GL, i);}
}//队列的顺序存储结构
typedef struct
{char data[MAXVEX];int front;int rear;
}SqQueue;void InitQueue(SqQueue* Q)
{Q->front = 0;Q->rear = 0;
}void EnQueue(SqQueue* Q, int e)
{if ((Q->rear + 1) % MAXVEX == Q->front)return;Q->data[Q->rear] = e;Q->rear = (Q->rear + 1) % MAXVEX;
}void DeQueue(SqQueue* Q, int* e)
{if (Q->front == Q->rear)return;*e = Q->data[Q->front];Q->front = (Q->front + 1) % MAXVEX;}int QueueEmpty(SqQueue Q)
{return Q.front == Q.rear;
}//邻接表的广度优先遍历
void BFSTraverse(GraphAdjList GL)
{int i;EdgeNode* p;SqQueue Q;Q.front = Q.rear = 0;for (i = 0; i < GL.numVertexes; i++){visited[i] = 0;if (!visited[i]){visited[i] = 1;printf("%c ", GL.adjList[i].data);EnQueue(&Q, i);while (!QueueEmpty(Q)){DeQueue(&Q, &i);p = GL.adjList[i].firstedge;while (p){if (!visited[p->adjvex]){visited[p->adjvex] = 1;printf("%c ", GL.adjList[p->adjvex].data);EnQueue(&Q, p->adjvex);}p = p->next;}}}}
}int main()
{GraphAdjList GL;CreateALGraph(&GL);printf("DFS遍历顺序:");DFSTraverse(GL);printf("\n");printf("BFS遍历顺序:");BFSTraverse(GL);printf("\n");return 0;
}一点补充
下面补充一个小知识点,就是typedef定义数组类型,先看下面的代码是什么意思呢?
typedef struct VertexNode AdjList[MAXVEX];
上面语句的意思是:定义一个元素类型是 struct VertexNode,含有MAXVEX个元素的数组类型
换个例子:
typedef int vector[10];
vector v1,v2;
语句定义了vector类型的两个对象v1和v2,每个对象都是vector类型的一个数组,每个数组由10个整型元素所组成。
写在最后
上面的代码难免会有疏漏,如果各位大佬发现错误,请一定要指正🙏
👍🏻 点赞,你的认可是我创作的动力!
⭐ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!
相关文章:

【数据结构】邻接矩阵和邻接图的遍历
写在前面 本篇文章开始学习数据结构的图的相关知识,涉及的基本概念还是很多的。本文的行文思路:学习图的基本概念学习图的存储结构——本文主要介绍邻接矩阵和邻接表对每种结构进行深度优先遍历和广度优先遍历先识概念话不多说,狠活献上学习思想等等&…...
设计跳表(动态设置节点高度)
最近学习redis的zset时候,又看到跳表的思想,突然对跳表的设置有了新的思考 这是19年设计的跳表,在leetcode的执行时间是200ms 现在我对跳表有了新的想法 1、跳表的设计,类似二分查找,但是不是二分查找,比较…...

基于神经辐射场(Neural Radiance Fileds, NeRF)的三维重建- 简介(1)
Nerf简介 Nerf(neural Radiance Fileds) 为2020年ICCV上提出的一个基于隐式表达的三维重建方法,使用2D的 Posed Imageds 来生成(表达)复杂的三维场景。现在越来越多的研究人员开始关注这个潜力巨大的领域,也…...
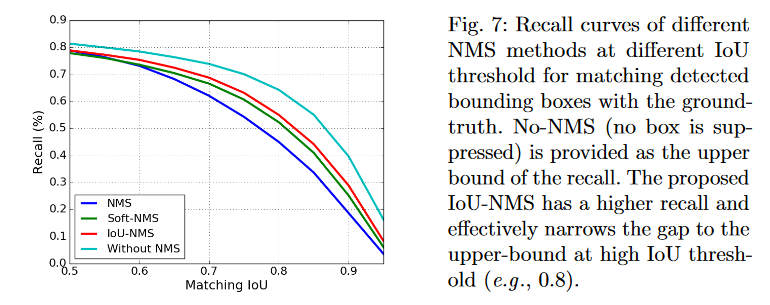
【AI面试】NMS 与 Soft NMS 的辨析
往期文章: AI/CV面试,直达目录汇总【AI面试】L1 loss、L2 loss和Smooth L1 Loss,L1正则化和L2正则化 一、NMS 非极大值抑制(Non-Maximum Suppression,NMS),并不是深度学习时期,目标…...
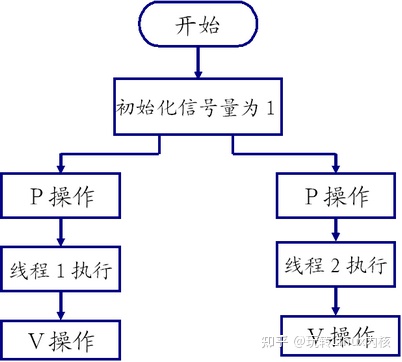
一文让你彻底理解Linux内核多线程(互斥锁、条件变量、读写锁、自旋锁、信号量)
一、互斥锁(同步) 在多任务操作系统中,同时运行的多个任务可能都需要使用同一种资源。这个过程有点类似于,公司部门里,我在使用着打印机打印东西的同时(还没有打印完),别人刚好也在…...
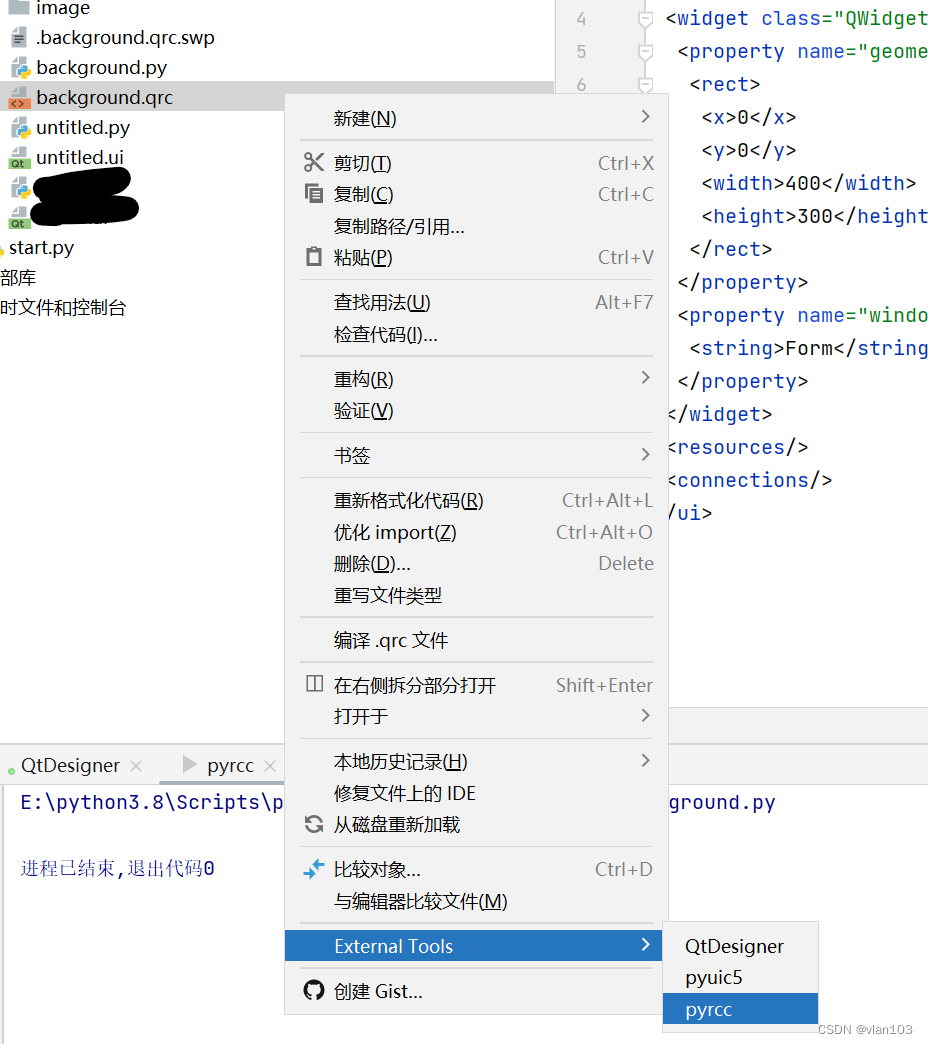
利用python写一个gui小公举--环境搭建
文章目录背景搭建环境安装必要库添加工具快捷方式检验背景 在实习过程中遇到一个问题,某项目是通过python代码实现的,而且需要一直修改参数实现功能,过程有些繁琐。虽然师兄用PHP study搭了一个网站用于查看结果,但是还是过于繁琐…...

英飞凌Tricore实战系列02_ENDINIT属性看门狗原理及应用
目录 1.概述2.ENDINIT功能及使用2.1 ENDINIT属性2.2 改写受ENDINIT保护寄存器的步骤3. Tricore 看门狗介绍及使用3.1 看门狗系统介绍3.1.1 安全看门狗介绍3.1.2 CPU看门狗介绍3.2 看门狗模式介绍3.2.1 Time-out模式3.2.2 正常模式(Normal Mode)3.2.3 禁用模式(Disabled Mode…...

Java Number类
Java Number 类是一个抽象类,它是所有数字类的基类。Java 中的数字类包括 Byte、Short、Integer、Long、Float 和 Double,它们都继承自 Number 类。Java Number 类提供了一些常用的方法,可以用于将数字类型转换为不同的格式,以及进…...
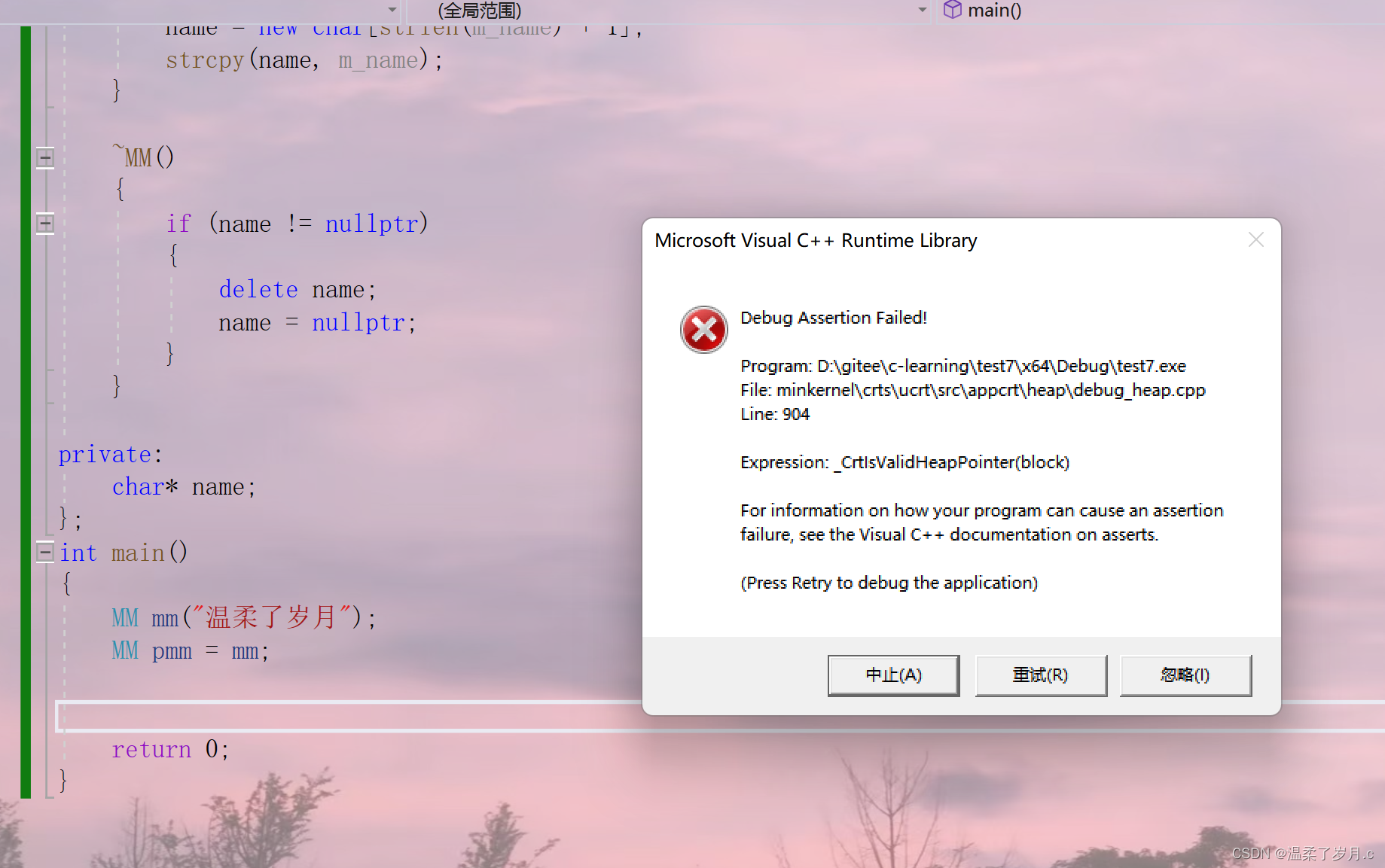
C++构造和析构
欢迎来观看温柔了岁月.c的博客 目前 设有C学习专栏 C语言项目专栏 数据结构与算法专栏 目前主要更新C学习专栏,C语言项目专栏不定时更新 待C专栏完毕,会陆续更新C项目专栏和数据结构与算法专栏 一周主要三更,星期三,星期五&#x…...
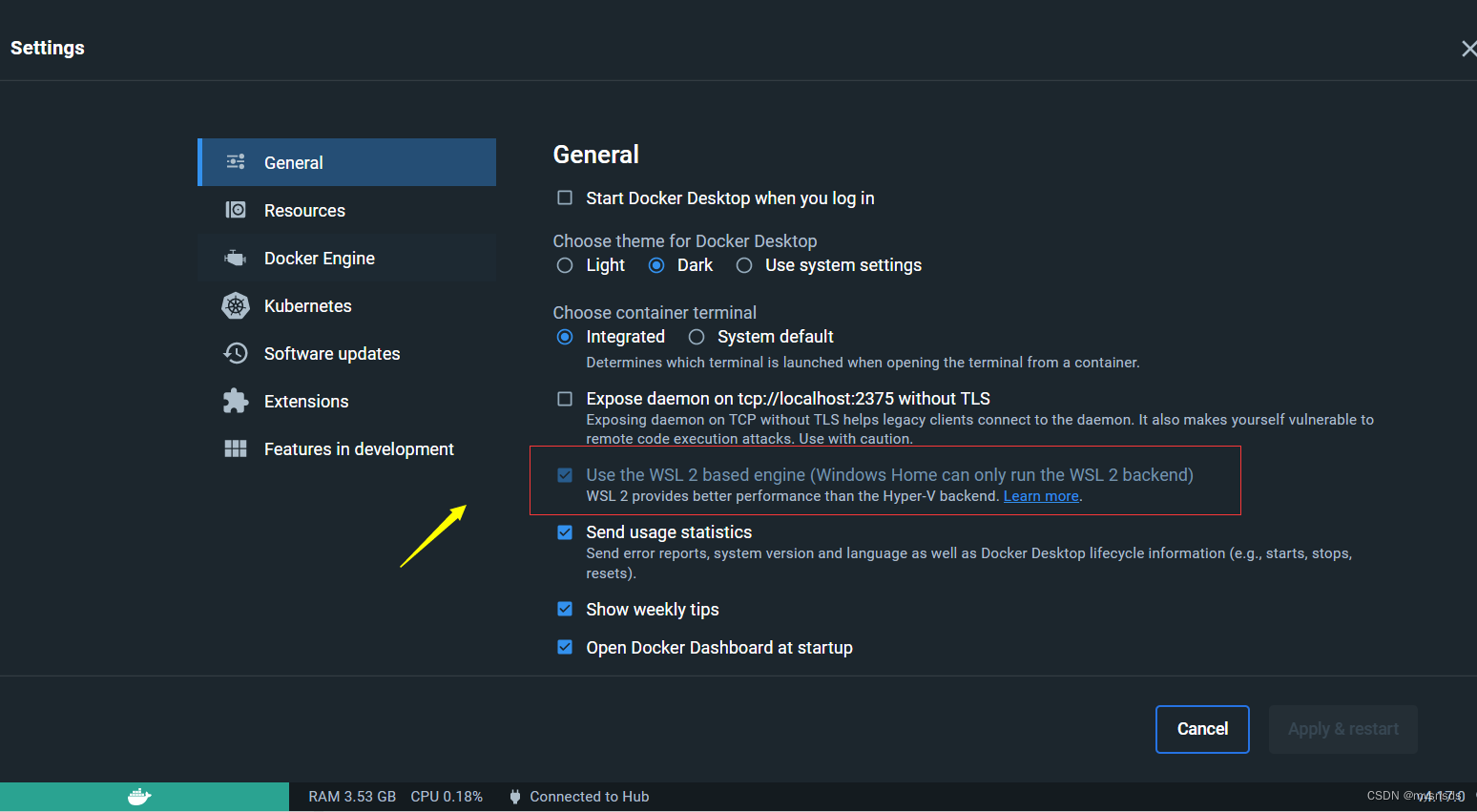
docker安装即docker连接mysql(window)
一 安装docker 1.什么是docker Docker容器与虚拟机类似,但二者在原理上不同。容器是将操作系统层虚拟化,虚拟机则是虚拟化硬件,因此容器更具有便携性、高效地利用服务器。 2.WSL2 WSL,即Windows Subsystem on Linux,中…...

HMM-维特比算法
HMM-维特比算法(viterbi)HMM回顾隐马科夫链解法:维特比算法(Viterbi)HMM回顾 最终的公式可以解释主要分为两个部分: P(xi|yi),发射概率,字面意思是从一个词性中发射/生成出某一个单…...
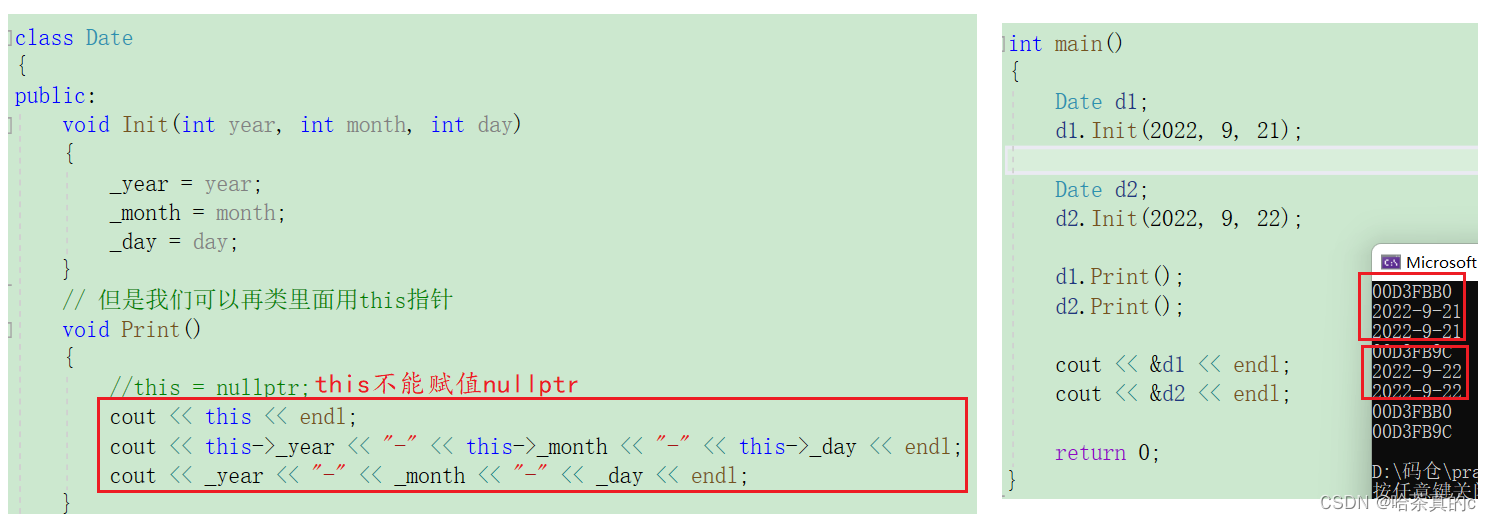
【C++初阶】2. 类和对象_1
1. 面向过程和面向对象的初步认识 2. 类的引入 C语言结构体中只能定义变量,在C中,结构体内不仅可以定义变量,也可以定义函数。比如: 之前在数据结构初阶中,用C语言方式实现的栈,结构体中只能定义变量&#…...

kotlin把函数作为参数转递给另一个函数
kotlin把函数作为参数转递给另一个函数 fun say(s: String, foo: (String) -> Unit) {print("hello")foo(s) }fun hi(str: String) {println(str) }fun main(args: Array<String>) {say("hello", ::hi) } 输出: hellohello...
海思嵌入式开发-005-OpenHarmony源码编译问题
海思嵌入式开发-005-OpenHarmony源码编译问题一、问题描述二、解决方案2.1解决原理2.2获取OpenHarmony 3.1.1 Release源码2.3最后解决问题,编译成功。一、问题描述 按照链接拉取master源码,出现如下问题,打开build.log文件 提示相应位置的文…...
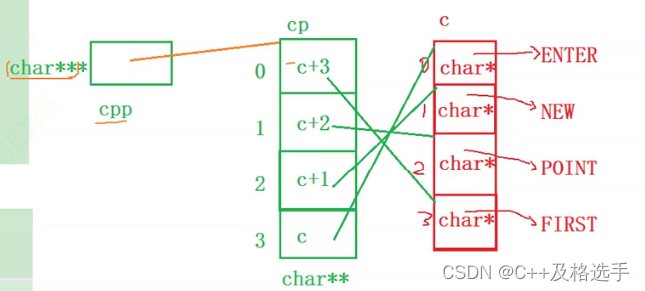
指针的进阶续(笔试题强化练习)
写在前面:在上次我们学习了指针的相关类型的知识,对指针家族的成员基本有了了解,这次让我们跟着一些题目来练习和补充一些知识,这有助于我们强化理解这些知识。 话不多说,我们马上开始: 1.指针和数组的笔…...

一个供参考的计算机的学习路线
本文是介绍如何成为一个Geek,一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人,避免走一些弯路。 仅代表个人想法,供批判性参考。 第一门入门的必备功课-语法与算法 什么是计算机?…...
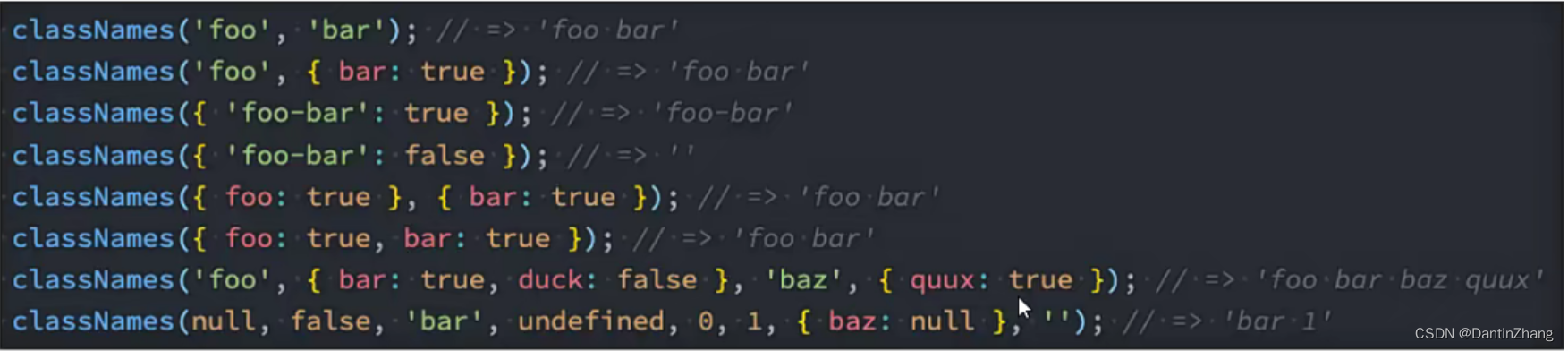
React(五):受控组件、高阶组件、Portals、Fragment、CSS的编写方式
React(五)一、受控组件1.什么是受控组件(v-model)2.收集表单数据:input和单选框3.收集表单数据:下拉框二、非受控组件三、高阶组件1.什么是高阶组件2.高阶组件的应用13.高阶组件的应用2-注入Context4.高阶组件的应用3-登录鉴权5.高…...
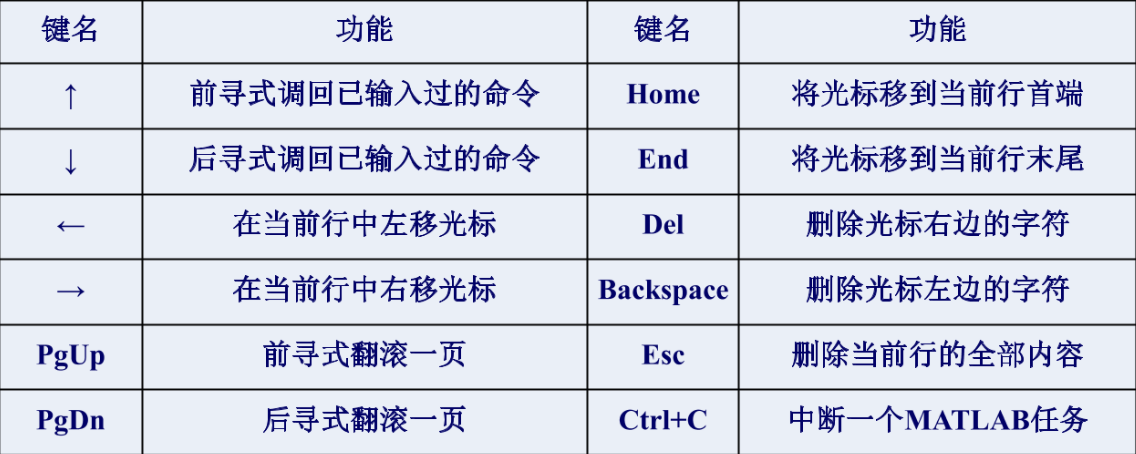
MATLAB——系统环境
MATLAB概述MATLAB的发展MATLAB:MATrix LABoratory1980年前后,Cleve Moler教授编写的Linpack 和Eispack的接口程序。1984年,MATLAB第1版(DOS版)1992年,MATLAB4.0版1994年,MATLAB 4.2版1997年,MATLAB 5.0版1999年&#x…...

2 GateWay工作流程+GateWay搭建
GateWay工作流程GateWay搭建 核心流程图如下: 核心概念: 客户端向 Spring Cloud Gateway 发出请求。如果Gateway Handler Mapping确定请求与路由匹配,则将其发送到Gateway Web Handler 处理程序。此处理程序通过特定于请求的Fliter链运行请求…...

【微信小程序】富文本rich-text的图片预览效果的几种方法
前言 使用原生小程序开发,实现在富文本rich-text中的图片预览效果的几种方法对比。 1.正则wx.previewImage(有明显不足) 一个不需要用额外组件或插件的方法: 思路:使用正则把图片的url进行剖离出来,push…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
