百度搜索智能精选是什么东西、怎么加入?
百度搜索智能精选是什么?
提问及具体展示如上图,这是白杨SEO一个好友提问的。他是觉得这个入口篇幅这么大,做宣传推广不错,问我是什么,怎么可以加入进去?
其实这就是百度搜索智能精选,只能是PC端才能这么显示,百度APP上没有这样。再白话一点,百度搜索智能精选就是百度PC端搜索设置里一个实时预测功能,方便用户快速找到自己想要的。
比如,我随便搜一下木工怎么学,如图。你也可以去搜索试试。
百度搜索智能精选入口及怎么开启?
百度PC端搜索智能精选入口不是固定的,只有当你输入关键词时搜索结果才能展示,比如上面的“木工怎么学”。
百度PC端搜索智能精选怎么开启?其实如果你现在用百度PC搜,默认就是开启的,除非你关闭掉。
打开你的百度,然后点右上角的设置,然后点搜索设置,就出来了,如图:
百度搜索智能精选怎么加入?
百度PC端搜索智能精选是花钱进入的吗?不是的。我相信除了提问这个朋友,其它朋友也想知道怎么可以加入进去,是不是?
其实,这并不是百度一个新的产品,其实这种样式七年前百度移动端就有了,这几年百度的精选摘要也是这种形式。如图:
只是,百度现在搜索智能精选的结果不再是调到第三方网站或者百度自己产品如百家号文章上面,而是直接以https://answer.baidu.com/这样网址显示。
怎么加入呢?白杨SEO有二点建议:
第一点,就是你做的这个词一定是小众的产品,或者知道人并不多
第二点,也是最重要的,就是针对这个产品的内容一定要按照顺序 1、2、3、4这样列好,如果有小标题也要列好,逻辑一定要清楚。同时内容准确、无误,全面更好。
以上这2点做到,大概率有可能出现。为什么是大概?因为你还要保证你的内容被收录啊。所以如果你对百度SEO基础感兴趣,也想学习可以看《白杨SEO全网SEO训练营视频课程介绍》关于百度SEO里的课程哈。
作者介绍:
白杨SEO,专注SEO十年,全网SEO流量实战派,对互联网精准流量有深入研究。
相关文章:

百度搜索智能精选是什么东西、怎么加入?
百度搜索智能精选是什么? 提问及具体展示如上图,这是白杨SEO一个好友提问的。他是觉得这个入口篇幅这么大,做宣传推广不错,问我是什么,怎么可以加入进去? 其实这就是百度搜索智能精选,只能是P…...

小程序开发平台:全功能小程序商城功能 带完整的安装代码包以及搭建教程
移动互联网的普及和用户对购物体验要求的提高,传统电商网站已经不能满足用户的需求。因此,许多商家开始将目光转向小程序商城,以提供更加便捷、高效的购物体验。然而,由于小程序开发门槛较高,许多商家和开发者对于小程…...
)
Vue3生命周期 VS Vue2生命周期(小记)
概念:Vue组件实例在创建时要经历一系列的初始化步骤,在此过程中Vue会在合适的时机,调用特定的函数,从而让开发者有机会在特定阶段运行自己的代码,这些特定的函数统称为:生命周期钩子。 规律: 生…...
MYSQL基本查询(CURD:创建、读取、更新、删除)
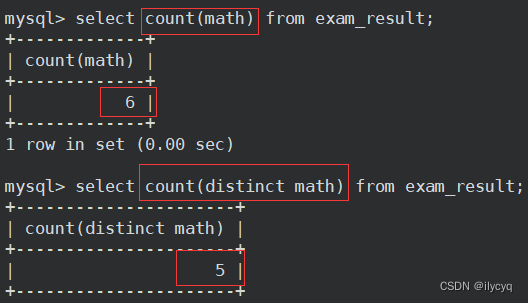
文章目录 前言一、Create1.全列插入2.指定列插入3.插入否则更新4.替换 二、Retrieve1.SELECT列2.WHERE条件3.结果排序4.筛选分页结果 三、Update四、Delete1.删除数据2.截断表 五、插入查询结果六、聚合函数 前言 操作关系型数据库的编程语言,定义了一套操作关系型…...

头歌C语言指针进阶
目录 第1关:输出若干个学生成绩中的最高分.要求用指针函数实现 任务描述 第2关:采用指针变量表示地址的方法输入输出数组中的个元素 任务描述 相关知识(略) 编程要求 第3关:用指针实现数组循环移动 任务描述 第…...

民安智库-公共健身场所满意度调研
公共健身场所作为市民锻炼身心的热门场所,其满意度情况对于提升市民生活质量具有重要意义。民安智库近期受客户委托对某市进行了一项全面的公共健身场所满意度调查,旨在了解市民的需求与期望,为改善健身环境提供依据。 在本次调研中…...

《HTML 简易速速上手小册》第3章:HTML 的列表与表格(2024 最新版)
文章目录 3.1 创建无序和有序列表(📝🌟👍 信息的时尚搭配师)3.1.1 基础示例:创建一个简单的购物清单3.1.2 案例扩展一:创建一个旅行计划清单3.1.3 案例扩展二:创建一个混合列表 3.2 …...

IBeginDragHandler,IEndDragHandler,IDragHandler拖拽接口
IBeginDragHandler, IEndDragHandler, 和 IDragHandler 是Unity的接口,用于处理拖拽相关的功能。需要引用 UnityEngine.EventSystems。 IBeginDragHandler 这个接口定义了一个方法,该方法在玩家开始拖拽一个对象时被调用。它通常用于初始化拖拽相关的变量…...

面试经典 150 题 ---- 删除排序数组中的重复项
面试经典 150 题 ---- 删除排序数组中的重复项 删除排序数组中的重复项方法一:双指针 删除排序数组中的重复项 方法一:双指针 有是一个原地修改的题目,大概率依旧是双指针。 定义 right 表示遍历数组到达的下标位置,left 指针表…...

深度学习(6)---Transformer
文章目录 一、介绍二、架构2.1 Multi-head Attention2.2 Encoder(编码器)2.3 Decoder(解码器) 三、Encoder和Decoder之间的传递四、Training五、其他介绍5.1 Copy Mechanism5.2 Beam Search 一、介绍 1. Transformer是一个Seq2Seq(Sequence-to-Sequence)…...
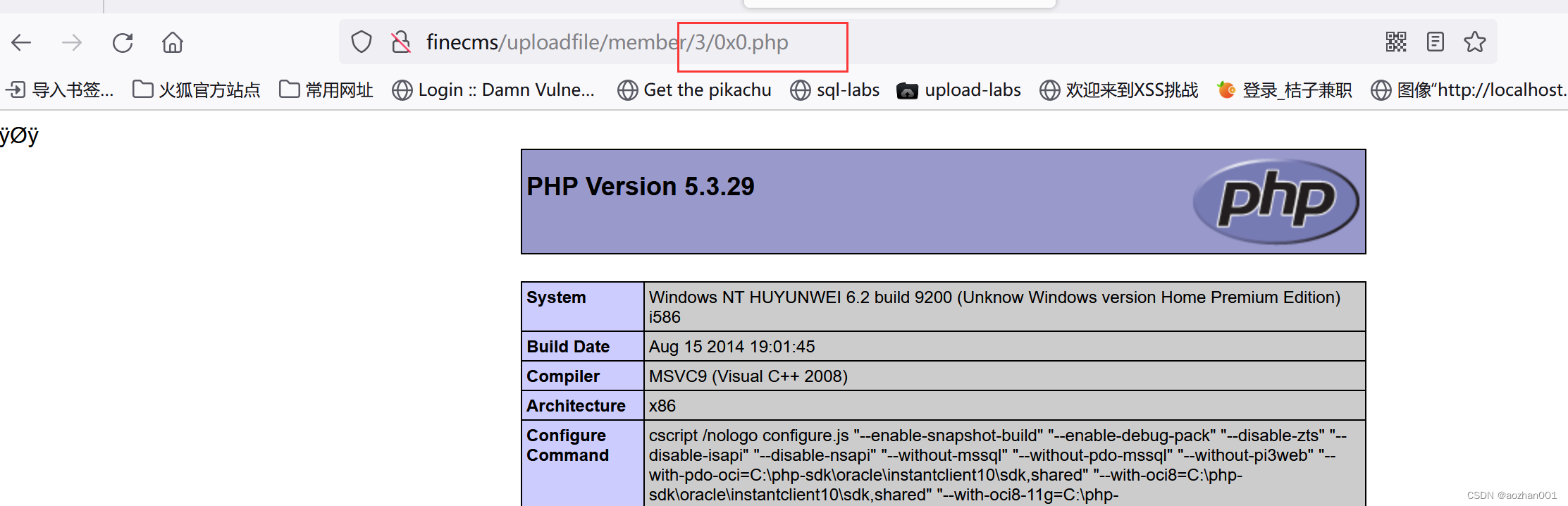
day34WEB 攻防-通用漏洞文件上传黑白盒审计逻辑中间件外部引用
目录 一,白盒审计-Finecms-代码常规-处理逻辑 黑盒思路:寻找上传点抓包修改突破获取状态码及地址 审计流程:功能点-代码文件-代码块-抓包调试-验证测试 二,白盒审计-CuppaCms-中间件-.htaccess 三,白盒审计-Metin…...

面试经典 150 题 ---- 移除元素
面试经典 150 题 ---- 移除元素 移除元素方法一:双指针方法二:双指针优化 移除元素 方法一:双指针 题目要求在原数组的基础进行元素的删除,所以输出的数组长度一定小于原数组的长度,因此可以使用双指针,r…...

12.如何将图像转化为矩阵形式
read_image (Image, printer_chip/printer_chip_01) *获取图片大小 get_image_size (Image, Width, Height) *获取区域里各点(每个点)的坐标 *Image 输入参数, *Rows 输出参数 数组, *Columns 输出参数,数组 get_region_points (Image, Rows…...
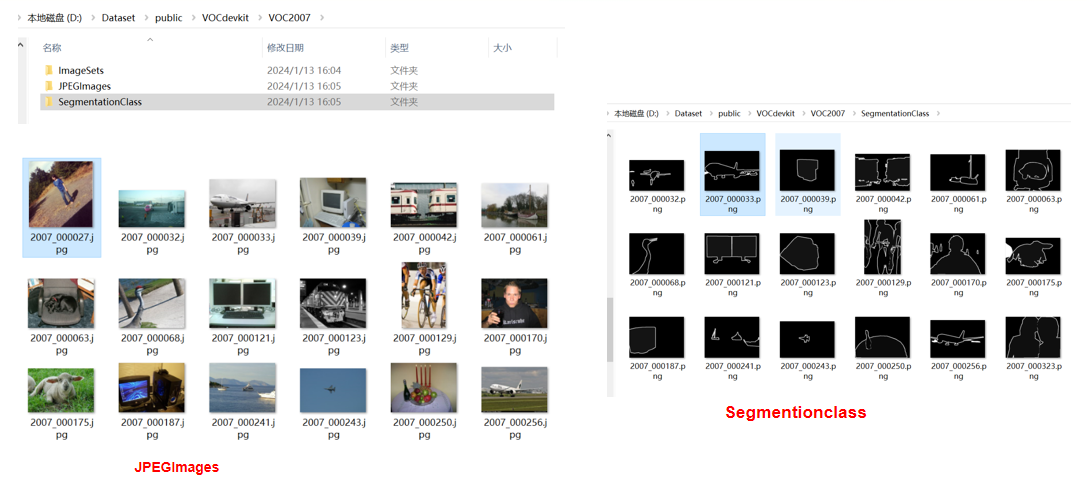
语义分割(2) :自定义Dataset和Dataloader
文章目录 1. 数据处理1.1 标签转换(json2mask和json2yolo)1.1.1 json2mask1.1.2 json2yolo 1.2 划分数据集1.2 不规范的标签图片处理1.3 批量修改图片后缀 2 自定义Dataset 和 Dataloader2.1 自定义Dataset2.1.1 数据增强(1) 对图像进行缩放并且进行长和宽的扭曲(2) 随机翻转图…...
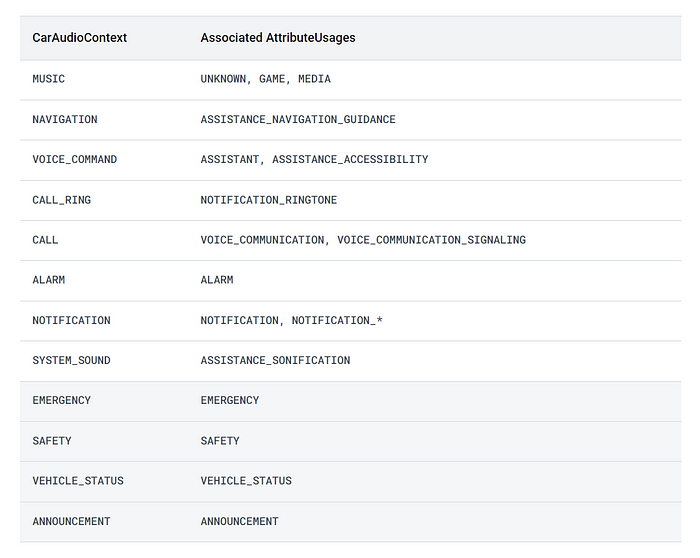
Android Automotive:在路上释放 Android 操作系统的力量
Android Automotive:在路上释放 Android 操作系统的力量 Android 在汽车行业的历程车载信息娱乐系统 (IVI) 的演变汽车中的 Android:演变和进步Android 汽车操作系统的崛起Polestar 2:开创 Android 汽车体验Android 开源项目 (AOSP) 及其他项…...

从零开始做题:逆向 ret2shellcode orw
1.题目信息 BUUCTF在线评测 下载orw时防病毒要关闭 2.题目分析 orw是open、read、write的简写。有时候binary会通过prctl、seccomp进行沙箱保护,并不能getshell。只能通过orw的方式拿到flag。 fdopen(‘./flag’); # 打开flag文件,得到fd…...
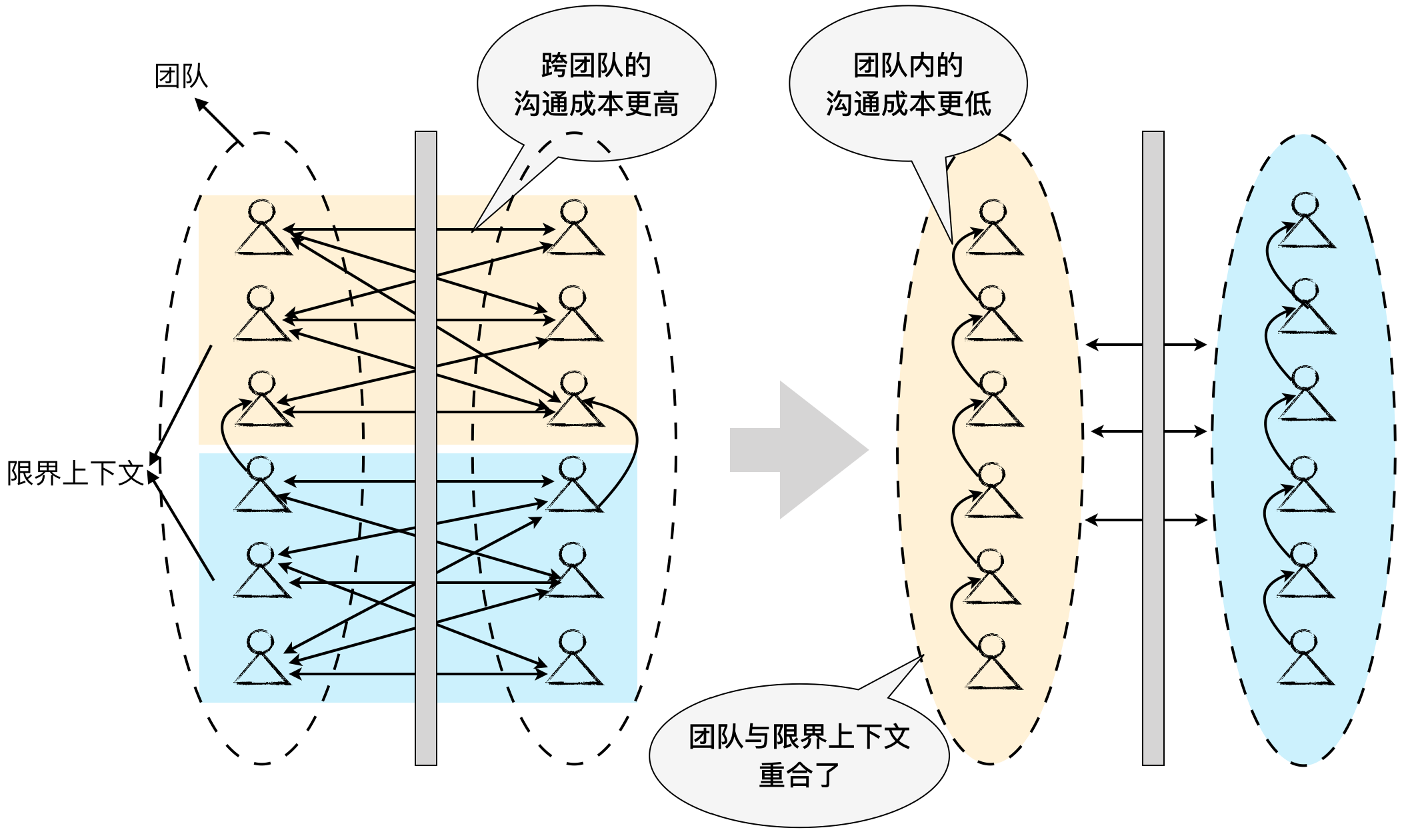
【DDD】学习笔记-限界上下文的控制力
引入限界上下文的目的,不在于如何划分,而在于如何控制边界。因此,我们就需要将对限界上下文的关注转移到对控制边界的理解。显然,对应于统一语言,限界上下文是语言的边界,对于领域模型,限界上下…...

springboot(ssm医院疫情防控系统 疫苗核酸预约系统Java系统
springboot(ssm医院疫情防控系统 疫苗核酸预约系统Java系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7&a…...

go语言中的Mutex
Golang以其并发性Goroutines而闻名。不仅是并发,还有更多。 因此,在这种情况下,我们必须确保多个goroutines不应该同时试图修改资源,从而导致冲突。 为了确保资源一次只能被一个goroutine访问,我们可以使用一个叫做syn…...

Vue的状态管理Vuex
文章目录 一、介绍二、install三、store1、介绍2、创建并全局引入3、单一状态树4、多模块状态树(无命名空间)5、多模块状态树(有命名空间) 本人最近在找工作,有推荐的小伙伴私我,不胜感激。 一、介绍 Vue…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
