MATLAB - 仿真单摆的周期性摆动
系列文章目录
前言
本例演示如何使用 Symbolic Math Toolbox™ 模拟单摆的运动。推导摆的运动方程,然后对小角度进行分析求解,对任意角度进行数值求解。
一、步骤 1:推导运动方程
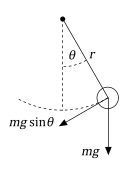
摆是一个遵循微分方程的简单机械系统。摆最初静止在垂直位置。当摆移动一个角度 θ 并释放时,重力将其拉回静止位置。它的动量会使它过冲并到达 -θ 角(如果没有摩擦力),以此类推。由于重力的作用,钟摆运动的恢复力为 -mgsinθ。因此,根据牛顿第二定律,质量乘以加速度必须等于 -mgsinθ。
syms m a g theta(t)
eqn = m*a == -m*g*sin(theta)eqn(t) = a m=−g m sin(θ(t))对于长度为 r 的摆锤,摆锤的加速度等于角加速度乘以 r。
用子项代替 a。
syms r
eqn = subs(eqn,a,r*diff(theta,2))
使用 isolate 隔离公式中的角加速度。
eqn = isolate(eqn,diff(theta,2))将常数 g 和 r 合并为一个参数,也称为固有频率。
syms omega_0
eqn = subs(eqn,g/r,omega_0^2)二、步骤 2:运动方程线性化
运动方程是非线性的,因此难以用解析法求解。假设角度很小,利用 sinθ 的泰勒展开式将方程线性化。
syms x
approx = taylor(sin(x),x,'Order',2);
approx = subs(approx,x,theta(t))运动方程变成了线性方程。
eqnLinear = subs(eqn,sin(theta(t)),approx)三、步骤 3:分析求解运动方程
使用 dsolve 求解方程 eqnLinear。将初始条件指定为第二个参数。使用 assume 假设 ω0 为实数,简化解法。
syms theta_0 theta_t0
theta_t = diff(theta);
cond = [theta(0) == theta_0, theta_t(0) == theta_t0];
assume(omega_0,'real')
thetaSol(t) = dsolve(eqnLinear,cond)四、步骤 4:ω0 的物理意义
项 ω 0 t 称为相位。余弦函数和正弦函数每 2π 重复一次。改变 ω 0 t 变化 2π 所需的时间称为时间周期。
时间周期 T 与摆长的平方根成正比,与质量无关。对于线性运动方程,时间周期与初始条件无关。
五、步骤 5:绘制摆的运动图
绘制小角度近似的摆运动图。
定义物理参数:
- 重力加速度
- 摆长
gValue = 9.81;
rValue = 1;
omega_0Value = sqrt(gValue/rValue);
T = 2*pi/omega_0Value;设置初始条件。
theta_0Value = 0.1*pi; % Solution only valid for small angles.
theta_t0Value = 0; % Initially at rest.将物理参数和初始条件代入一般解法。
vars = [omega_0 theta_0 theta_t0];
values = [omega_0Value theta_0Value theta_t0Value];
thetaSolPlot = subs(thetaSol,vars,values);绘制谐摆运动图。
fplot(thetaSolPlot(t*T)/pi, [0 5]);
grid on;
title('Harmonic Pendulum Motion');
xlabel('t/T');
ylabel('\theta/\pi');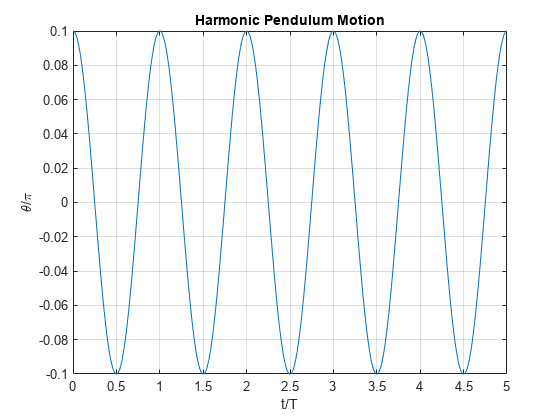
求出 θ(t) 的解后,想象一下摆的运动。
x_pos = sin(thetaSolPlot);
y_pos = -cos(thetaSolPlot);
fanimator(@fplot,x_pos,y_pos,'ko','MarkerFaceColor','k','AnimationRange',[0 5*T]);
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'),'AnimationRange',[0 5*T]);
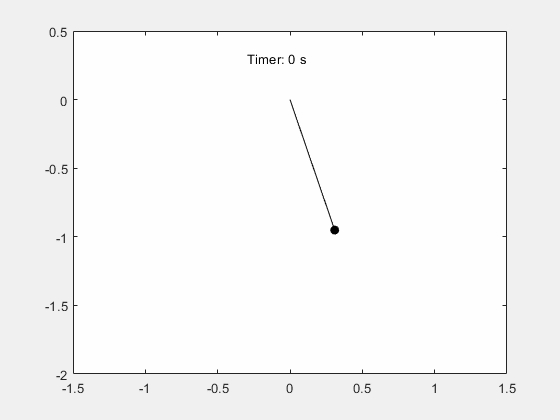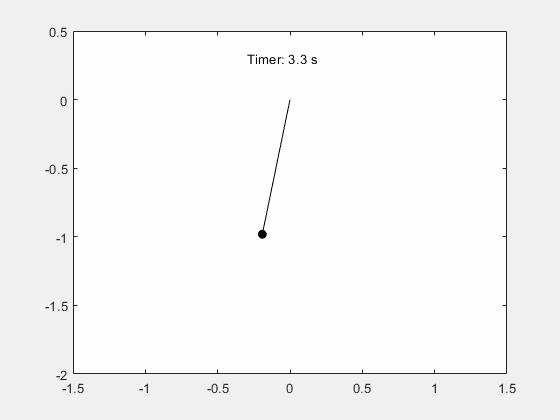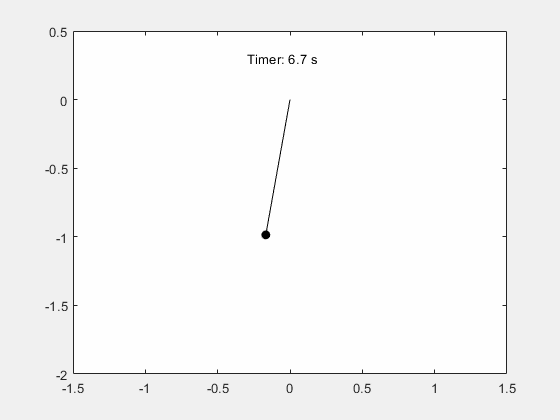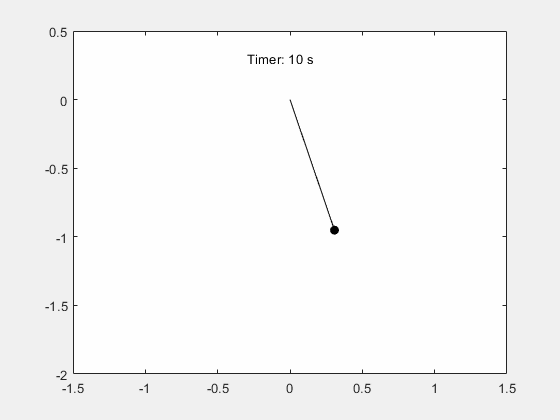
fanimator(@(t) text(-0.3,0.3,"Timer: "+num2str(t,2)+" s"),'AnimationRange',[0 5*T]);
输入 playAnimation 命令播放钟摆运动的动画。
六、步骤 6:使用恒定能量路径确定非线性摆运动
为了理解摆的非线性运动,请使用总能量方程来直观显示摆的运动轨迹。总能量是守恒的。
使用三角函数特性 和关系式
重写比例能量。
由于能量守恒,摆的运动可以用相空间中的恒定能量路径来描述。相空间是一个抽象空间,坐标为 θ 和 dθ/dt。使用 fcontour 将这些路径可视化。
syms theta theta_t omega_0
E(theta, theta_t, omega_0) = (1/2)*(theta_t^2+(2*omega_0*sin(theta/2))^2);
Eplot(theta, theta_t) = subs(E,omega_0,omega_0Value);figure;
fc = fcontour(Eplot(pi*theta, 2*omega_0Value*theta_t), 2*[-1 1 -1 1], ...'LineWidth', 2, 'LevelList', 0:5:50, 'MeshDensity', 1+2^8);
grid on;
title('Constant Energy Contours in Phase Space ( \theta vs. \theta_t )');
xlabel('\theta/\pi');
ylabel('\theta_t/2\omega_0');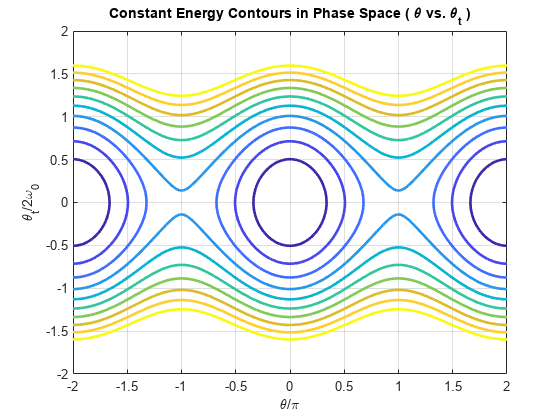
恒定能量等值线围绕 θ 轴和 dθ/dt 轴对称,沿 θ 轴呈周期性分布。图中显示了两个行为截然不同的区域。
等值线图的较低能量相互靠近。摆锤在两个最大角度和速度之间来回摆动。摆锤的动能不足以克服重力能,使摆锤绕一圈。

等值线图中的高能量不会自行闭合。摆锤始终沿着一个角度方向运动。钟摆的动能足以克服重力能,使钟摆能够绕一圈。

七、步骤 7:求解非线性运动方程
非线性运动方程是二阶微分方程。使用 ode45 求解器对这些方程进行数值求解。由于 ode45 只接受一阶系统,因此请将系统简化为一阶系统。然后生成函数句柄,作为 ode45 的输入。
将二阶 ODE 重写为一阶 ODE 系统。
syms theta(t) theta_t(t) omega_0
eqs = [diff(theta) == theta_t;diff(theta_t) == -omega_0^2*sin(theta)]
eqs = subs(eqs,omega_0,omega_0Value);
vars = [theta, theta_t];求出系统的质量矩阵 M 和方程 F 的右边。
[M,F] = massMatrixForm(eqs,vars)
M 和 F 指的就是这种形式。
为简化进一步计算,可将系统改写为 的形式。
f = M\F
使用 odeFunction 将 f 转换为 MATLAB 函数句柄。生成的函数句柄是 MATLAB ODE 求解器 ode45 的输入。
f = odeFunction(f, vars)f = function_handle with value:@(t,in2)[in2(2,:);sin(in2(1,:)).*(-9.81e+2./1.0e+2)]八、步骤 8:求解封闭能量等值线的运动方程
使用 ode45 求解封闭能量等值线的 ODE。
从能量等值线图来看,封闭等值线满足条件 . 将 θ 和 dθ/dt 的初始条件存储在变量 x0 中。
x0 = [0; 1.99*omega_0Value];指定一个从 0 秒到 10 秒的时间间隔,用于求解。这个时间间隔允许摆锤经历两个完整的周期。
tInit = 0;
tFinal = 10;求解 ODE。
sols = ode45(f,[tInit tFinal],x0)sols = struct with fields:solver: 'ode45'extdata: [1x1 struct]x: [0 3.2241e-05 1.9344e-04 9.9946e-04 0.0050 0.0252 0.1259 0.3449 0.6020 0.8591 1.1161 1.3597 1.5996 1.8995 2.2274 2.4651 2.7028 2.9567 3.2138 3.4709 3.7150 3.9511 4.2483 4.5759 4.8239 5.0719 5.3182 5.5764 5.8346 6.0803 ... ] (1x45 double)y: [2x45 double]stats: [1x1 struct]idata: [1x1 struct]
sols.y(1,:) 表示角位移 θ,sols.y(2,:) 表示角速度 dθ/dt。
绘制闭合路径解。
figure;yyaxis left;
plot(sols.x, sols.y(1,:), '-o');
ylabel('\theta (rad)');yyaxis right;
plot(sols.x, sols.y(2,:), '-o');
ylabel('\theta_t (rad/s)');grid on;
title('Closed Path in Phase Space');
xlabel('t (s)');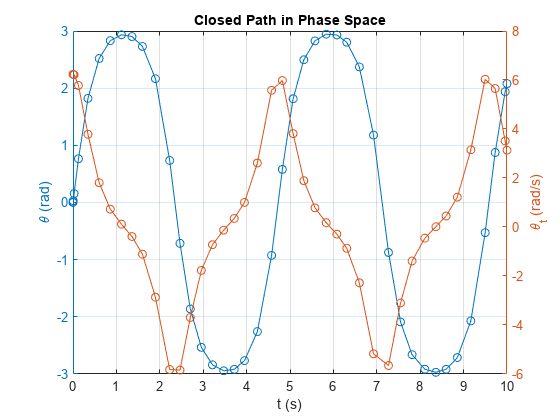
可视化钟摆的运动。
x_pos = @(t) sin(deval(sols,t,1));
y_pos = @(t) -cos(deval(sols,t,1));
figure;
fanimator(@(t) plot(x_pos(t),y_pos(t),'ko','MarkerFaceColor','k'));
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'));
fanimator(@(t) text(-0.3,1.5,"Timer: "+num2str(t,2)+" s"));
输入 playAnimation 命令播放钟摆运动的动画。
九、步骤 9:开放式能量等值线的求解
使用 ode45 求解开放式能量等值线的 ODE。从能量等值线图来看,开放式等值线满足条件 .
x0 = [0; 2.01*omega_0Value];
sols = ode45(f, [tInit, tFinal], x0);绘制开放式能量等值线的解。
figure;yyaxis left;
plot(sols.x, sols.y(1,:), '-o');
ylabel('\theta (rad)');yyaxis right;
plot(sols.x, sols.y(2,:), '-o');
ylabel('\theta_t (rad/s)');grid on;
title('Open Path in Phase Space');
xlabel('t (s)');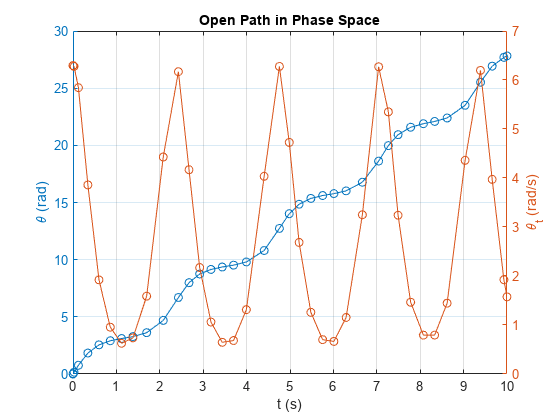
可视化钟摆的运动。
x_pos = @(t) sin(deval(sols,t,1));
y_pos = @(t) -cos(deval(sols,t,1));
figure;
fanimator(@(t) plot(x_pos(t),y_pos(t),'ko','MarkerFaceColor','k'));
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'));
fanimator(@(t) text(-0.3,1.5,"Timer: "+num2str(t,2)+" s"));
输入 playAnimation 命令播放钟摆运动的动画。
相关文章:

MATLAB - 仿真单摆的周期性摆动
系列文章目录 前言 本例演示如何使用 Symbolic Math Toolbox™ 模拟单摆的运动。推导摆的运动方程,然后对小角度进行分析求解,对任意角度进行数值求解。 一、步骤 1:推导运动方程 摆是一个遵循微分方程的简单机械系统。摆最初静止在垂直位置…...
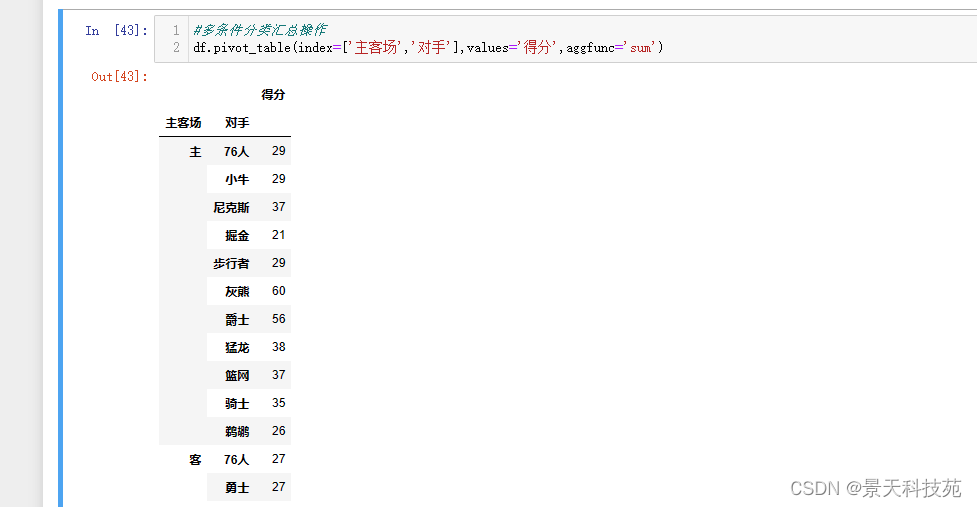
Pandas进阶--map映射,分组聚合和透视pivot_table详解
文章目录 1.Pandas的map映射(1)映射(2)map充当运算工具 2.数据分组和透视(1)分组统计 - groupby功能 是pandas最重要的功能(2)聚合agg 3.透视表pivot_table(1)…...

Visual Studio 和Clion配置Cocos2d-x环境
Visual Studio 和Clion配置Cocos2d-x环境 我就不贴图片的,懒得上传图床。懒。开发环境: 系统: Window11 编译器: CMake MSVC 开发工具:Clion or Visual Studio 请自行配置好,Python2.7,和Cmake Cocos2d-x下载…...
【百度Apollo】本地调试仿真:加速自动驾驶系统开发的利器
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《linux深造日志》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下…...

ztest中ddof起什么作用
⭐️ statsmodels 中 ztest 基本使用 statsmodels 也是一个强大的统计分析库,提供了丰富的统计模型和检验功能。对于 Z 检验,statsmodels 提供了 ztest 函数。 以下是使用 statsmodels 进行 Z 检验的示例: from statsmodels.stats.weights…...

linux 主机无法联网问题
主机不能联网 一 查看当前ip ping路由 ifconfig wlan0 wlan0: flags4163<UP,BROADCAST,RUNNING,MULTICAST> mtu 1500inet 192.168.2.78 netmask 255.255.255.0 broadcast 192.168.2.255ping 192.168.2.1查看是否能ping通 二 查看路由表 route -n Destination G…...

2024/1/27 备战蓝桥杯 1-1
目录 求和 0求和 - 蓝桥云课 (lanqiao.cn) 成绩分析 0成绩分析 - 蓝桥云课 (lanqiao.cn) 合法日期 0合法日期 - 蓝桥云课 (lanqiao.cn) 时间加法 0时间加法 - 蓝桥云课 (lanqiao.cn) 扫雷 0扫雷 - 蓝桥云课 (lanqiao.cn) 大写 0大写 - 蓝桥云课 (lanqiao.cn) 标题…...
支持下一代网络IpV6的串口服务器,IpV6串口485接口转网口
和IPv4比较,IPv6有两个极具吸引力的特点:一个是IPv6采用的128位地址格式,而IPv4采用32位的地址格式,因此IPv6使地址空间增大了296;另一个是IPv6物联网数据业务具有更强的支持能力,成为未来物联网的重要协议…...

uniapp H5 实现上拉刷新 以及 下拉加载
uniapp H5 实现上拉刷新 以及 下拉加载 1. 先上图 下拉加载 2. 上代码 <script>import DragableList from "/components/dragable-list/dragable-list.vue";import {FridApi} from /api/warn.jsexport default {data() {return {tableList: [],loadingHi…...
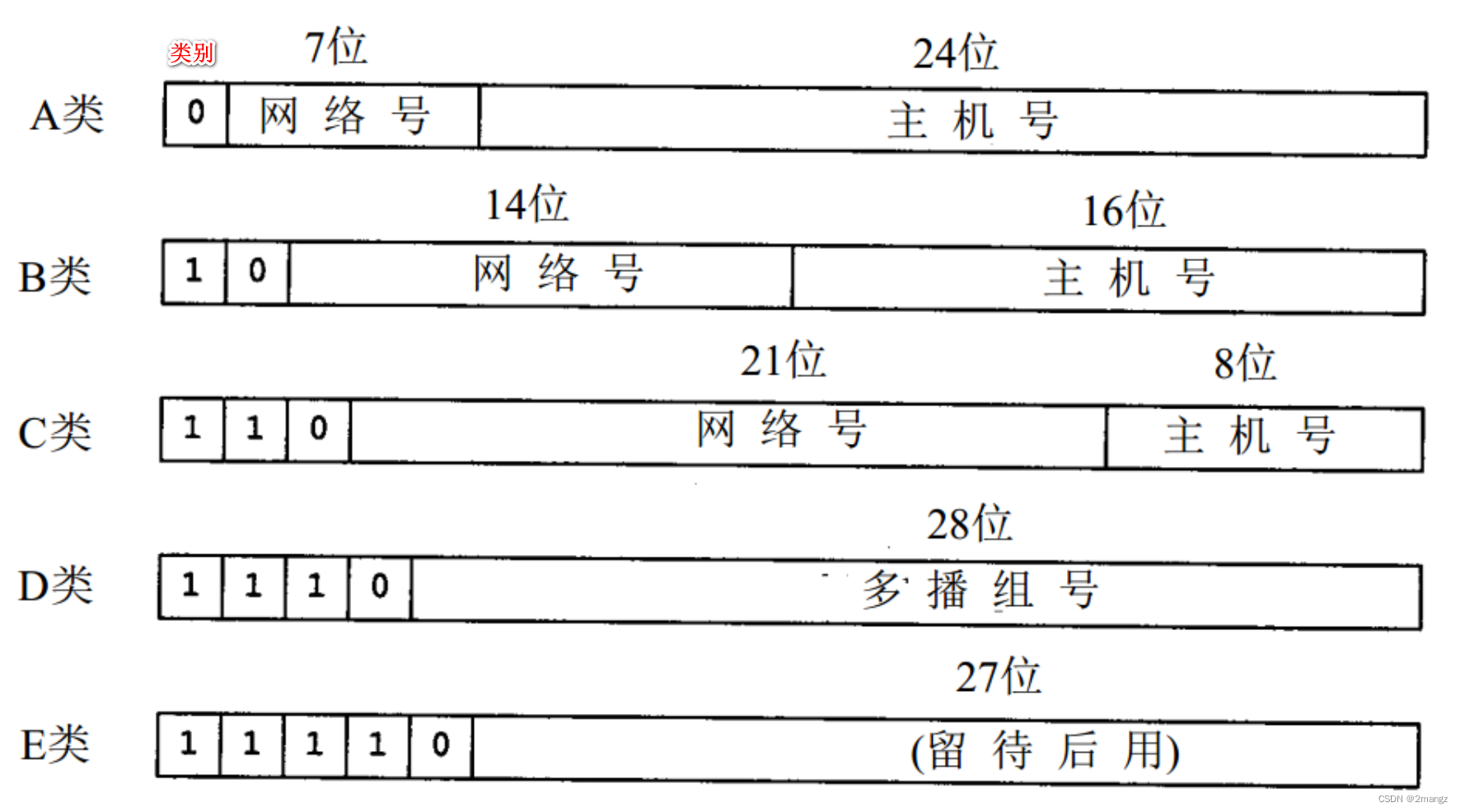
网络工程师必学知识:2、IPv4和IPv6地址划分
网络工程师必学知识:2、IPv4和IPv6地址划分 1.概述:2.IPv4:地址划分:有类划分,无类划分。一、有类划分:分为5类。ABCDE,掩码分别位8、16、24、28、27取值范围:出类别bit不变…...

Rust - 变量
不管学什么语言好像都得从变量开始,不过只需要懂得大概就可以了。 但在Rust里不先把变量研究明白后面根本无法进行… 变量绑定 变量赋值❌ 变量绑定✔️ Rust中没有“赋值”一说,而是称为绑定。 int a 3; //C中的变量赋值 a 3; //python中的…...

【Linux】压缩脚本、报警脚本
一、压缩搅拌 要求: 写一个脚本,完成如下功能 传递一个参数给脚本,此参数为gzip、bzip2或者xz三者之一; (1) 如果参数1的值为gzip,则使用tar和gzip归档压缩/etc目录至/backups目录中,并命名为/backups/etc…...

用Flask打造一个大模型智能问答WEB网站
目前已经有很多类似GPT的大模型开源,可以提供类似ChatGPT的智能问答功能。我也基于这些开源模型,用Flask来建立一个智能问答网站,可以方便用户建立自己的ChatGPT系统。 这个网站需要提供用户登录功能,对已登录的用户,可以在网站上提出问题,并由大模型处理后返回答案。演…...

学习python第三天
一.数据类型 1.获取数据类型 x 10 print(type(x))""" 输出 <class int> """2.复数类型(complex)详解 复数(Complex)是 Python 的内置类型,直接书写即可。换句话说,…...
(M)UNITY三段攻击制作
三段攻击逻辑 基本逻辑: 人物点击攻击按钮进入攻击状态(bool isAttack) 在攻击状态下, 一旦设置的触发器(trigger attack)被触发,设置的计数器(int combo)查看目前攻击…...
PHP的线程安全与非线程安全模式选哪个
曾经初学PHP的时候也很困惑对线程安全与非线程安全模式这块环境的选择,也未能理解其中意。近来无意中看到一个教程对线程安全(饿汉式),非线程安全(懒汉式)的描述,虽然觉得现在已经能够很明了透彻…...
asdf安装不同版本的nodejs和yarn和pnpm
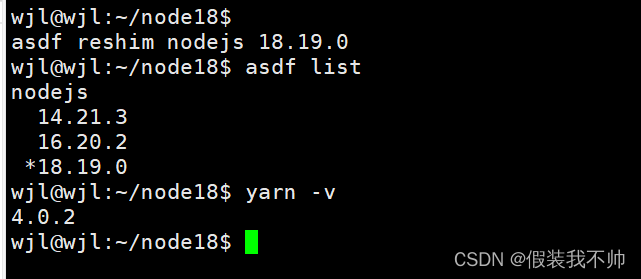
安装asdf 安装nodejs nodejs版本 目前项目中常用的是14、16和18 安装插件 asdf plugin add nodejs https://github.com/asdf-vm/asdf-nodejs.git asdf plugin-add yarn https://github.com/twuni/asdf-yarn.git可以查看获取所有的nodejs版本 asdf list all nodejs有很多找…...

Spring的事件监听机制
这里写自定义目录标题 1. 概述(重点)2. ApplicationEventMulticaster2.1 SimpleApplicationEventMulticaster2.2 AbstractApplicationEventMulticaster 3. ApplicationListener3.1 注册监听器3.2 自定义 4. SpringApplicationRunListeners 1. 概述&#…...
Zookeeper分布式命名服务实战
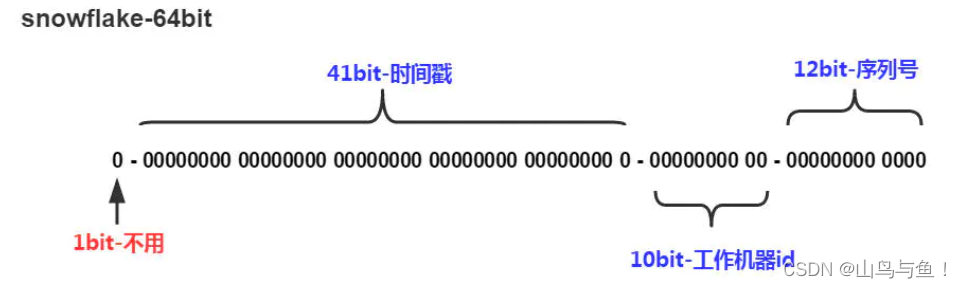
目录 分布式命名服务 分布式API目录 分布式节点的命名 分布式的ID生成器 分布式的ID生成器方案: 基于Zookeeper实现分布式ID生成器 基于Zookeeper实现SnowFlakeID算法 分布式命名服务 命名服务是为系统中的资源提供标识能力。ZooKeeper的命名服务主要是利用Z…...
)
DEV-C++ ege.h库 绘图教程(六)
一、前情回顾 DEV-C ege.h库 绘图教程(一) DEV-C ege.h库 绘图教程(二) DEV-C ege.h库 绘图教程(三) DEV-C ege.h库 绘图教程(四) DEV-C ege.h库 绘图教程(五)…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
