运动编辑学习笔记
目录
跳舞重建:
深度运动重定向
Motion Preprocessing Tool
anim_utils
MotionBuilder
跳舞重建:
https://github.com/Shimingyi/MotioNet
深度运动重定向
https://github.com/DeepMotionEditing/deep-motion-editin
游锋生/deep-motion-editing

Motion Preprocessing Tool
用于骨架动画和统计模型的可视化和编辑工具。它使用 vis_utils 的 OpenGL 渲染器,并提供了基于 anim_utils 的动画重定向和编辑功能。使用集成的数据库浏览器,可以从 https://motion.dfki.de 下载动作。数据库的代码在一个单独的仓库中,因此也可以设置自定义数据库。
https://github.com/eherr/motion_preprocessing_tool
anim_utils
https://github.com/eherr/anim_utils
from anim_utils.animation_data import BVHReader, MotionVector, SkeletonBuilder bvh = BVHReader("example.bvh")
mv = MotionVector()
mv.from_bvh_reader(bvh)
skeleton = SkeletonBuilder().load_from_bvh(bvh)
point_clouds = []
for frame in mv.frames: point_cloud = [] for j in skeleton.animated_joints: p = skeleton.nodes[j].get_global_position(frame) point_cloud.append(p) point_clouds.append(point_cloud)MotionBuilder
相关文章:

运动编辑学习笔记
目录 跳舞重建: 深度运动重定向 Motion Preprocessing Tool anim_utils MotionBuilder 跳舞重建: https://github.com/Shimingyi/MotioNet 深度运动重定向 https://github.com/DeepMotionEditing/deep-motion-editin 游锋生/deep-motion-editin…...
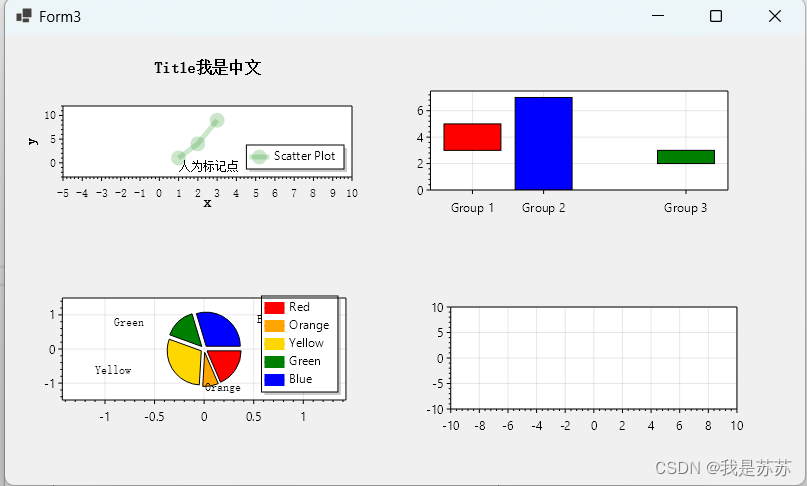
C#小结:ScottPlot 5.0在VS2022桌面开发的应用(以winform为例)
目录 一、官网文档地址 二、在VS2022中安装Scottplot 三、拖动Scottplot 四、使用Scottplot 五、效果图 一、官网文档地址 官网地址:ScottPlot 5.0 食谱 本文内容来自于官网,选取了官网的一些比较好用的功能展示,如需学习更多功能&a…...

Jmeter性能测试: Jmeter 5.6.3 分布式部署
目录 一、实验 1.环境 2.jmeter 配置 slave 代理压测机 3.jmeter配置master控制器压测机 4.启动slave从节点检查 5.启动master主节点检查 6.运行jmeter 7.观察jmeter-server主从节点变化 二、问题 1.jmeter 中间请求和响应乱码 一、实验 1.环境 (1&#…...

跟着cherno手搓游戏引擎【15】DrawCall的封装
目标: Application.cpp:把渲染循环里的glad代码封装成自己的类: #include"ytpch.h" #include "Application.h"#include"Log.h" #include "YOTO/Renderer/Renderer.h" #include"Input.h"namespace YO…...
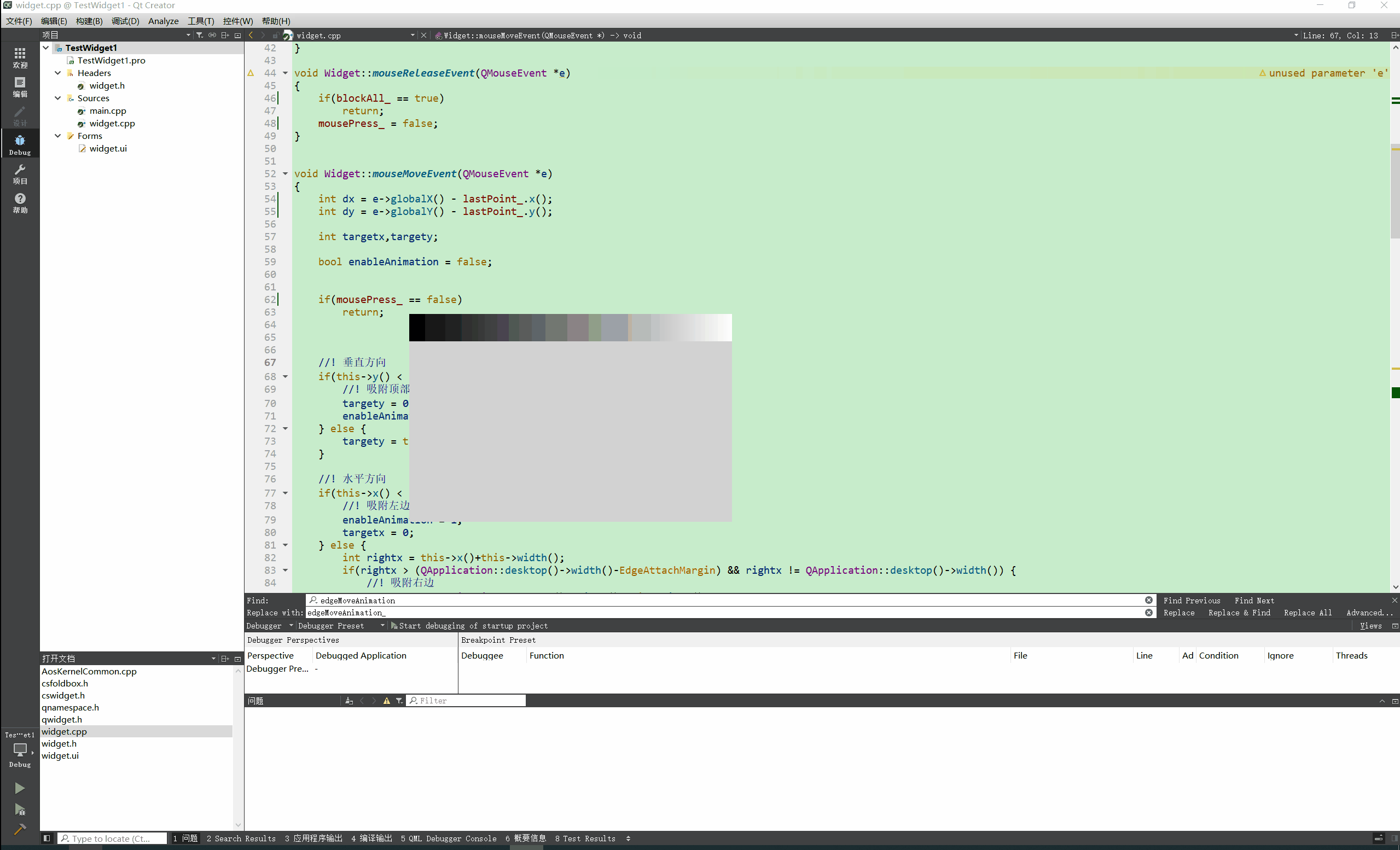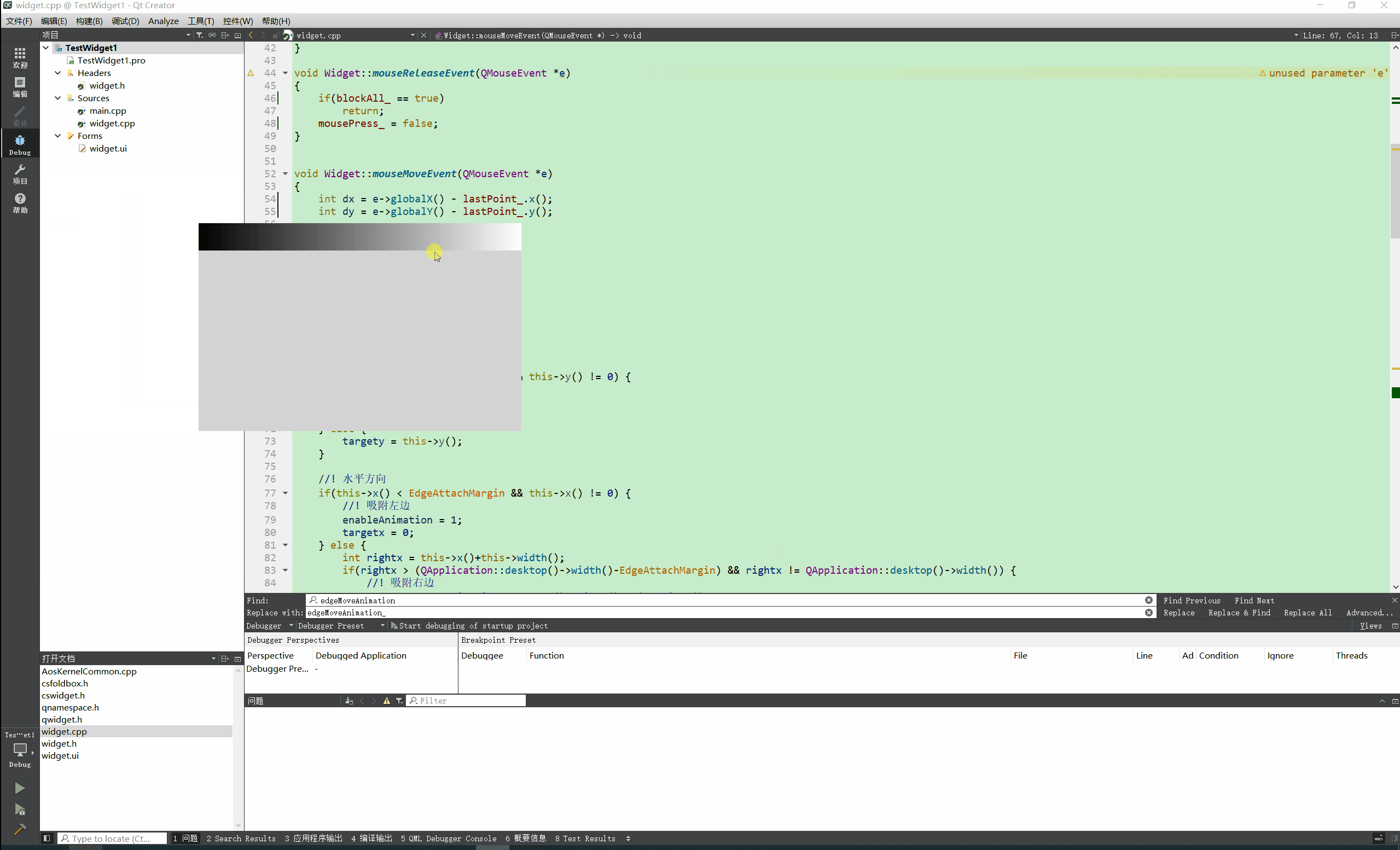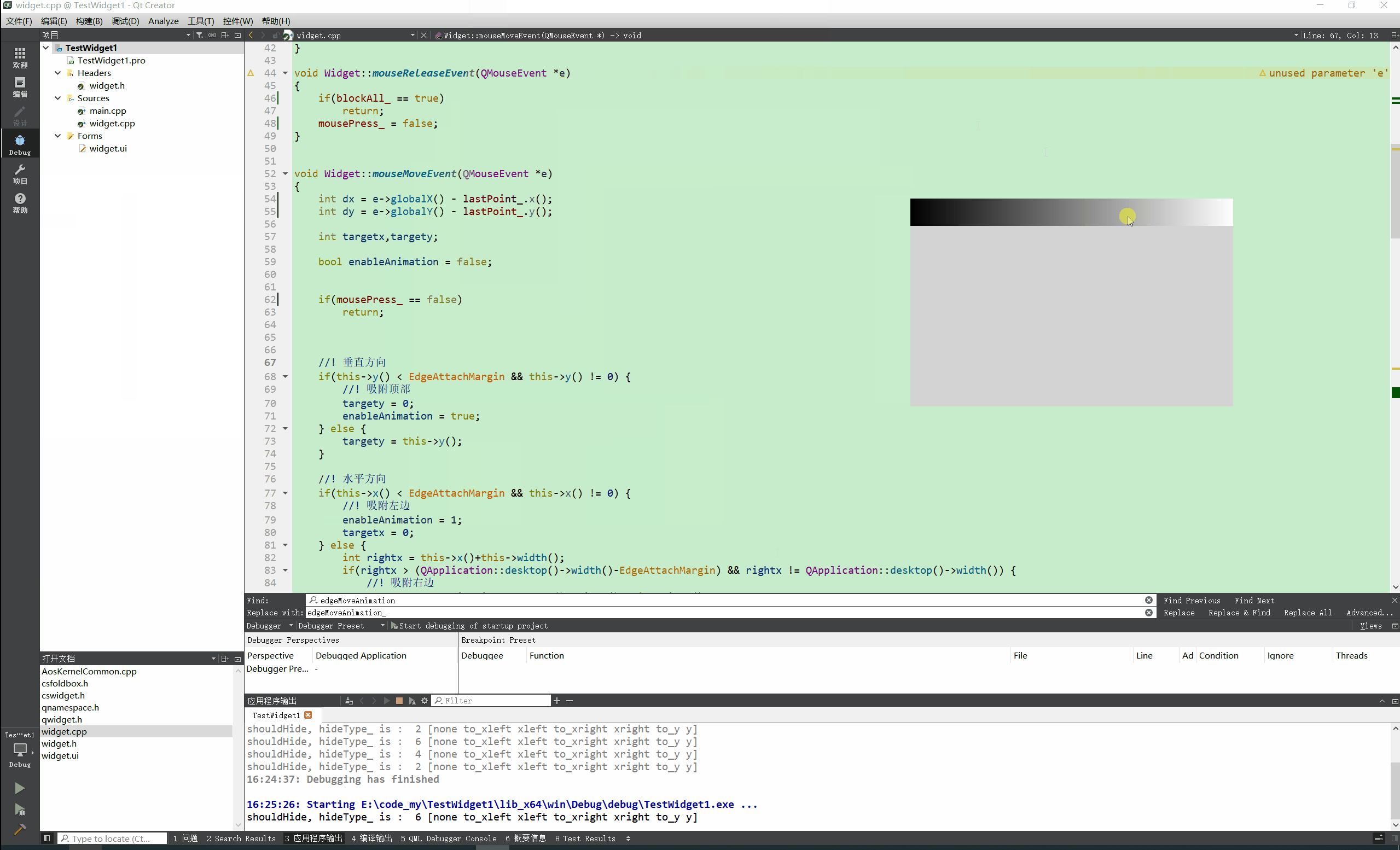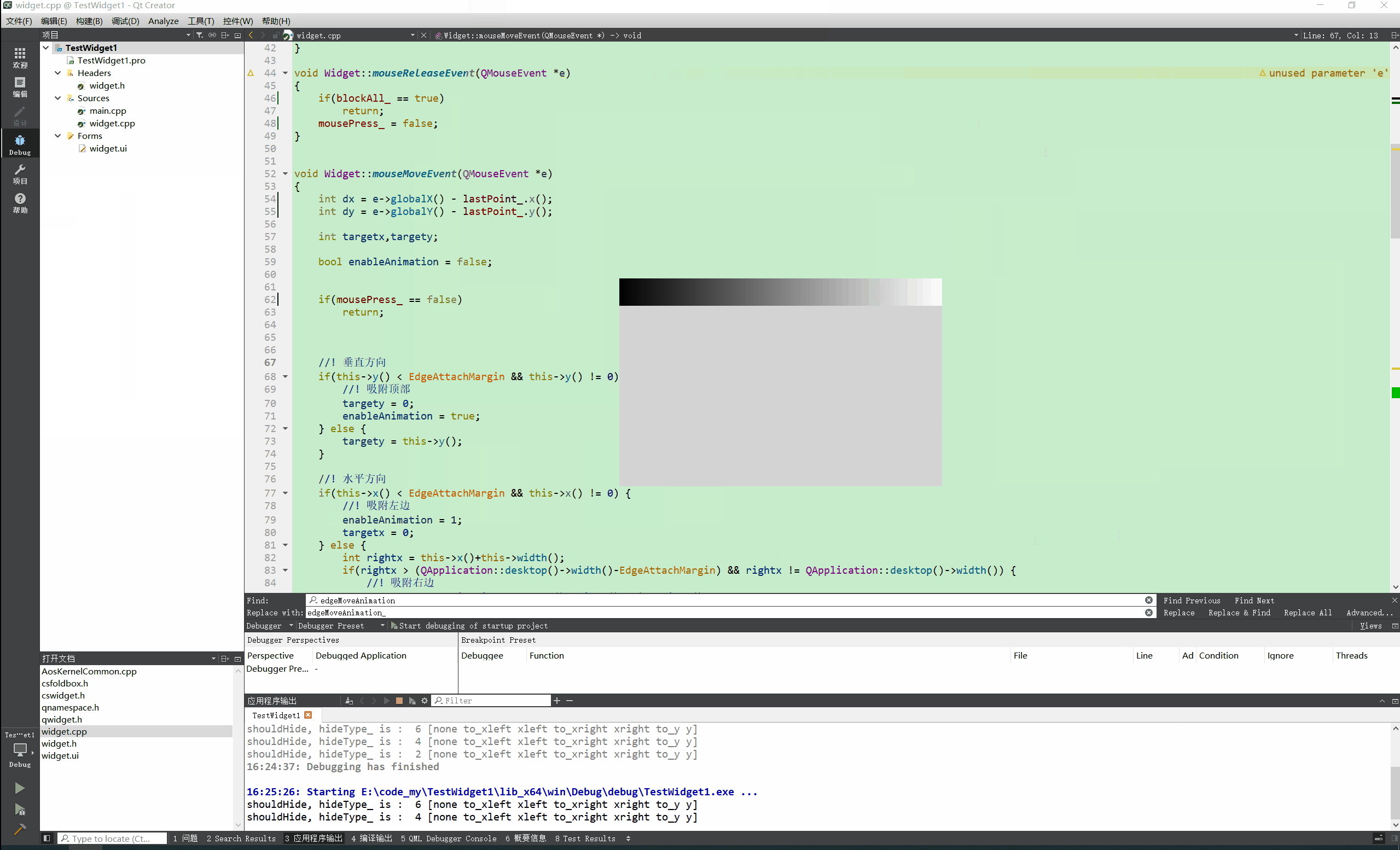
Qt实现窗口吸附屏幕边缘 自动收缩
先看效果: N年前的QQ就可以吸附到屏幕边缘,聊天时候非常方便,不用点击状态栏图标即可呼出QQ界面 自己尝试做了一个糙版的屏幕吸附效果。 关键代码: void Widget::mouseMoveEvent(QMouseEvent *e) {int dx e->globalX() - l…...
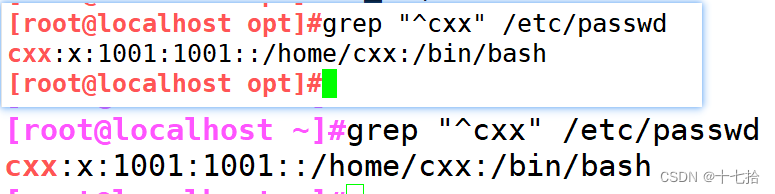
shell脚本之免交互
目录 一、Here Document 免交互 1、交互与免交互的概念 2、 Here Document 概述 二、Here Document 应用 1、使用cat命令多行重定向 2、使用tee命令多行重定向 3、使用read命令多行重定向 4、使用wc -l统计行数 5、使用passwd命令用户修改密码 6、Here Document 变量…...
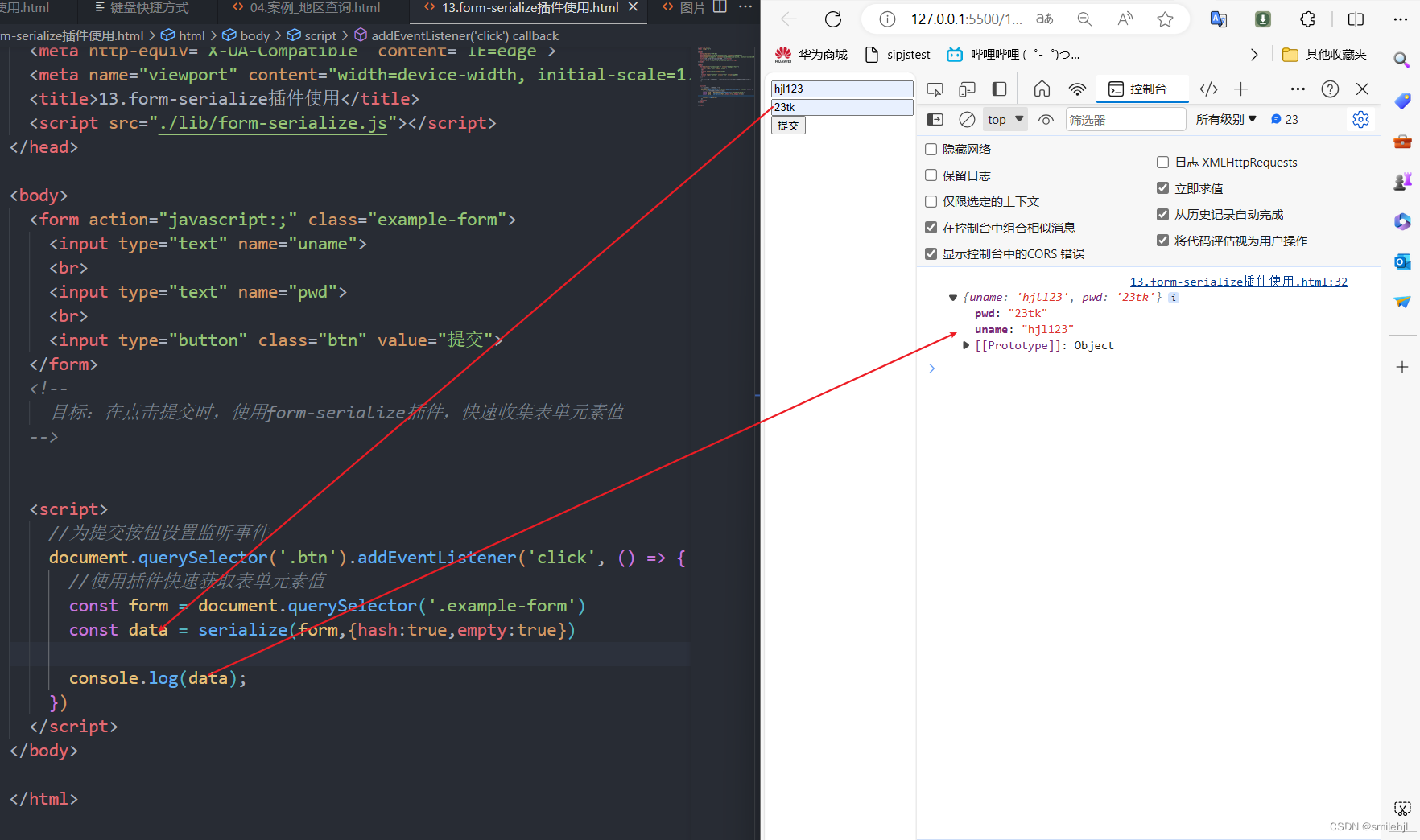
Ajax入门与使用
目录 ◆ AJAX 概念和 axios 使用 什么是 AJAX? 怎么发送 AJAX 请求? 如何使用axios axios 函数的基本结构 axios 函数的使用场景 1 没有参数的情况 2 使用params参数传参的情况 3 使用data参数来处理请求体的数据 4 上传图片等二进制的情况…...
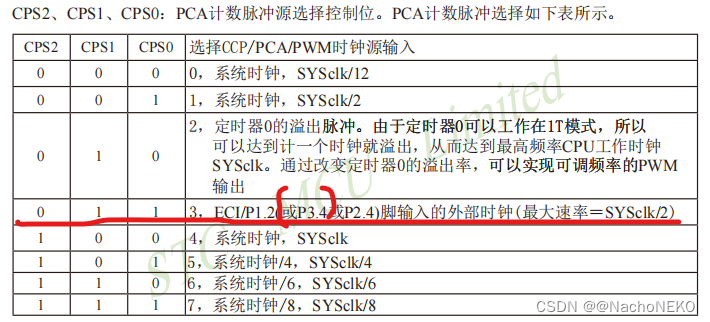
蓝桥杯备战——11.NE555测频
1.分析原理图 我们可以看到,上图就是一个NE555构建的方波发生电路,输出方波频率1.44/2(R8Rb3)C,如果有不懂NE555内部结构,工作原理的,可以到B站学习。实在不懂仿真也行,比如我下面就是仿真结果: 然后就是下…...

代码随想录算法训练营第三十三天|509. 斐波那契数 ,● 70. 爬楼梯 , 746. 使用最小花费爬楼梯
确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 代码随想录 视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩…...

Node.js 文件系统操作指南
文章目录 Node.js 文件系统操作完全指南一、引言二、基本文件操作2.1 读取文件2.2 写入文件2.3 追加内容到文件 三、文件与目录的创建与删除3.1 创建文件3.2 创建目录3.3 删除文件3.4 删除目录 四、文件与目录的信息查询4.1 检查文件或目录是否存在4.2 获取文件信息4.3 获取目录…...

Kotlin 协程1:深入理解withContext
Kotlin 协程1:深入理解withContext 引言 在现代编程中,异步编程已经变得非常重要。在 Kotlin 中,协程提供了一种优雅和高效的方式来处理异步编程和并发。在这篇文章中,我们将深入探讨 Kotlin 协程中的一个重要函数:wi…...
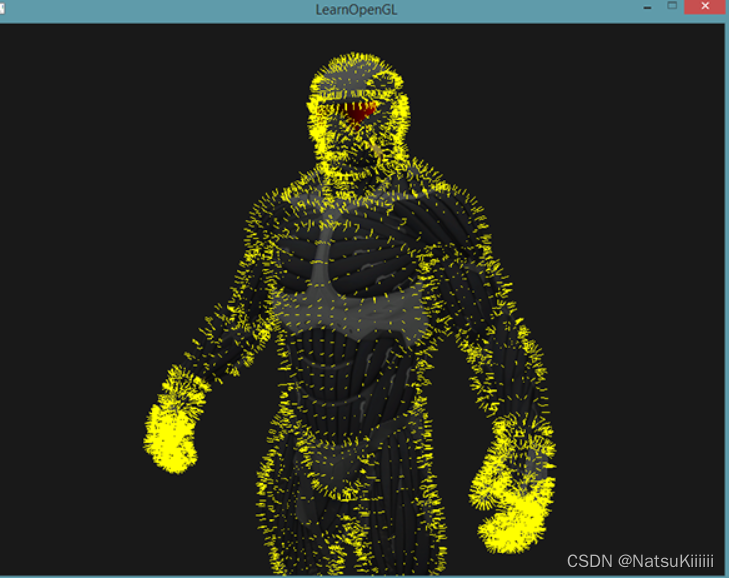
(自用)learnOpenGL学习总结-高级OpenGL-几何着色器
在顶点着色器和片段着色器中间还有一个几何着色器。 几何着色器的输入是一个图元的一组顶点,在几何着色器中进行任意变换之后再给片段着色器,可以变成完全不一样的图元、可以生成更多的顶点。 #version 330 core layout (points) in; layout (line_str…...
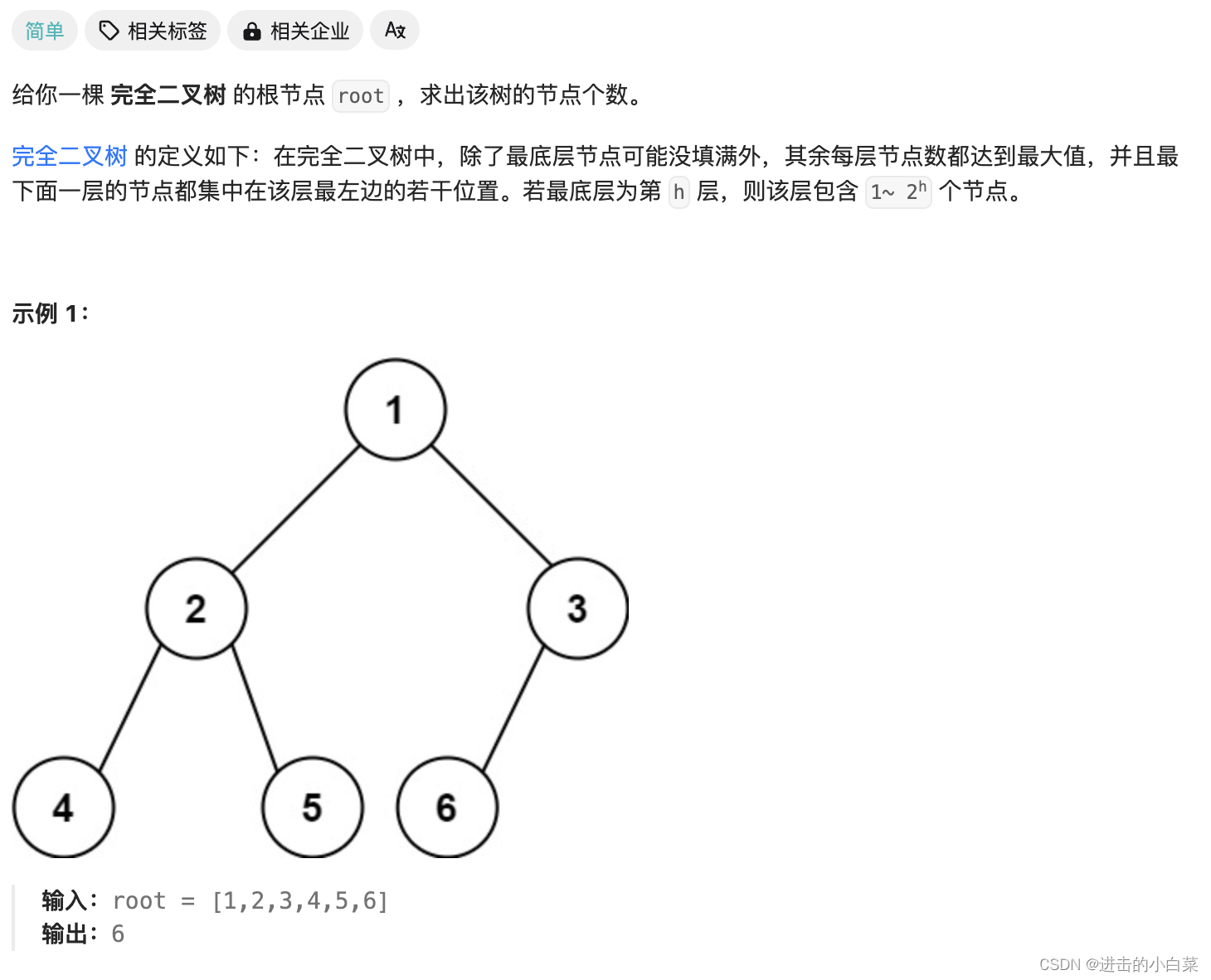
坚持刷题 | 完全二叉树的节点个数
Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数 题目 222.完全二叉树的节点个数 代码实现 class TreeNode {int val;TreeNode left, right;public TreeNode(int val) …...

K8S网络
一、介绍 k8s不提供网络通信,提供了CNI接口(Container Network Interface,容器网络接口),由CNI插件实现完成。 1.1 Pod通信 1.1.1 同一节点Pod通信 Pod通过虚拟Ethernet接口对(Veth Pair)与外部通信,Veth…...

【蓝桥杯51单片机入门记录】LED
目录 一、基础 (1)新建工程 (2)编写前准备 二、LED (1)点亮LED灯 (2)LED闪烁 延时函数的生成(stc-isp中生成) 实现 (3)流水灯…...
)
轻松使用python将PDF转换为图片(成功)
使用PyMuPDF(fitz)将PDF转换为图片 在处理PDF文件时,我们经常需要将PDF页面转换为图片格式,以便于在网页、文档或应用程序中显示。Python提供了多种方式来实现这一需求,本文将介绍如何使用PyMuPDF(也称为f…...

【目标检测】对DETR的简单理解
【目标检测】对DETR的简单理解 文章目录 【目标检测】对DETR的简单理解1. Abs2. Intro3. Method3.1 模型结构3.2 Loss 4. Exp5. Discussion5.1 二分匹配5.2 注意力机制5.3 方法存在的问题 6. Conclusion参考 1. Abs 两句话概括: 第一个真正意义上的端到端检测器最…...

[工具探索]Safari 和 Google Chrome 浏览器内核差异
最近有些Vue3的项目,使用了safari进行测试环境搞开发,发现页面存在不同程序的页面乱码情况,反而google浏览器没问题,下面我们就对比下他们之间的差异点: 日常开发google chrome占多数;现在主流浏览器 Goog…...

文本生成高清、连贯视频,谷歌推出时空扩散模型
谷歌研究人员推出了创新性文本生成视频模型——Lumiere。 与传统模型不同的是,Lumiere采用了一种时空扩散(Space-time)U-Net架构,可以在单次推理中生成整个视频的所有时间段,能明显增强生成视频的动作连贯性ÿ…...

时隔3年 | 微软 | Windows Server 2025 重磅发布
最新功能 以下是微软产品团队正在努力的方向: Windows Server 2025 为所有人提供的热补丁下一代 AD 活动目录和 SMB数据与存储Hyper-V 和人工智能还有更多… Ignite 发布视频 Windows Server 2025 Ignite Video 介绍 Windows Server 2022 正式发布日期是2021年…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
