C语言实现12种排序算法
1.冒泡排序
思路:比较相邻的两个数字,如果前一个数字大,那么就交换两个数字,直到有序。
- 时间复杂度:O(n^2),
- 稳定性:这是一种稳定的算法。
代码实现:
void bubble_sort(int arr[],size_t len){size_t i,j;for(i=0;i<len;i++){ bool hasSwap = false; //优化,判断数组是否已经有序,如果有序可以提前退出循环for(j=1;j<len-i;j++){ //这里j<len-i是因为最后面的肯定都是最大的,不需要多进行比较if(arr[j-1]>arr[j]){ //如果前一个比后一个大swap(&arr[j-1],&arr[j]); //交换两个数据hasSwap = true;} }if(!hasSwap){break; }}
}
2.插入排序
思路:把一个数字插入一个有序的序列中,使之仍然保持有序,如对于需要我们进行排序的数组,我们可以使它的前i个数字有序,然后再插入i+1个数字,插入到合适的位置使之仍然保持有序,直到所有的数字有序。
- 时间复杂度:O(n^2)
- 稳定性:稳定的算法
代码实现:
void insert_sort(int arr[],int len)
{int i,j;for(i=1;i<len;i++){int key = arr[i]; //记录当前需要插入的数据for(j= i-1;i>=0&&arr[j]>key;j--){ //找到插入的位置arr[j+1] = arr[j]; //把需要插入的元素后面的元素往后移}arr[j+1] = key; //插入该元素}
}
3.折半插入排序
思路:本质上是插入排序,但是通过半分查找法找到插入的位置,让效率稍微快一点。
- 时间复杂度:O(n^2),
- 稳定性:稳定的算法。
代码实现:
void half_insert_sort(int arr[],int len)
{int i,j;for(i=1;i<len;i++){int key = arr[i];int left = 0;int right = i-1;while(left<=right){ //半分查找找到插入的位置int mid = (left+right)/2;if(key<arr[mid]){right = mid-1; }else{left = mid+1; } }for(j=i-1;j>=left;j--){ //把后面的元素往后移arr[j+1]=arr[j]; }arr[j+1] = key; //插入元素}
}
4.希尔排序
思路:先取一个正整数d1<n,把所有序号相隔d1的数组元素放一组,组内进行直接插入排序;然后取d2<d1,重复上述分组和排序操作;直至di=1,即所有记录放进一个组中排序为止。
- 时间复杂度:O(n^1.3) ,算法效率上大大提高 。
- 稳定性:不稳定的算法。
- 代码实现
void shell_sort(int arr[],int len)
{ //本质上也是一种插入排序,避免了大量数据的移动,在每一组排序过后,每个数据已经到了大致的位置。int i,j;int step=0;for(step = len/2;step>=1;step=step/2){ //分组 分为step组,对每组的元素进行插入排序for(i=step;i<len;i++){int key = arr[i];for(j=i-step;j>=0&&arr[j]>key;j=j-step){arr[j+step] = arr[j]; } arr[j+step] = key;}}
}
5.选择排序
思路:通过循环找到最大值所在的位置,然后把最大值和最后一个元素进行交换,通过循环直到所有的数据有序。
- 时间复杂度:O(n^2)
- 稳定性:不稳定的算法
代码实现:
void select_sort(int arr[],size_t len)
{size_t i,j;for(i=0;i<len-1;i++){int max = 0; //最大值下标for(j=1;j<len-i;j++){if(arr[max]<arr[j]){ //找到最大值的下标max = j; } }if(max!=j-1){ swap(&arr[max],&arr[j-1]); //把最后一个元素和最大值进行交换}}
}
6.鸡尾酒排序
思路:选择排序的一种改进,一次循环直接找到最大值和最小值的位置,把最大值和最后一个元素进行交换,最小值和最前一个元素进行交换,所以最外层的循环只需要执行len/2次即可
- 时间复杂度:O(n^2)
- 稳定性:不稳定的算法
代码实现:
void cocktail_sort(int arr[],size_t len)
{size_t i,j;for(i=0;i<len/2;i++){int max = i; //最大值下标int min = i; //最小值下标for(j=i+1;j<len-i;j++){if(arr[max]<arr[j]){ //找到最大值下标max = j; } if(arr[min]>arr[j]){ //找到最小值下标min = j; }}if(max!=j-1){swap(&arr[max],&arr[j-1]); //交换最大值和未进行排序的最后一个元素}if(min == j-1){ //如果最小值在未进行排序的最后一个位置,那么经过最大值的交换,已经交换到了最大值所在的位置min = max; //把最小值的坐标进行改变}if(min!=i){swap(&arr[i],&arr[min]); //交换最小值和未进行排序的最前的元素}}
}
7.堆排序
思路:把数据进行大堆化,然后依次交换堆顶(最大值)和最后一个元素,在使堆顶重新大堆化,最后循环过后数组便有序。
最大堆调整(Max Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
创建最大堆(Build Max Heap):将堆中的所有数据重新排序
堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
- 时间复杂度:O(nlgn)
- 稳定性:不稳定的算法
代码实现:
void re_heap(int arr[],size_t index,size_t len)
{size_t child = 2*index+1; //左节点坐标int key = arr[index]; //当前节点值while(child<len){if(child+1<len&&arr[child]<arr[child+1]){ //如果右节点存在且右节点的值比左节点大,那就child记录较大字节点的坐标child++; } if(arr[child]>key){ //如果子节点的值比根节点的值大arr[index] = arr[child]; //改变根节点的值}else{break; }index = child;child = 2*index+1;}arr[index] = key; //插入记录好的值
}
void heap_sort(int arr[],size_t len)
{int i;for(i=len/2;i>=0;i--){re_heap(arr,i,len); //对第i个根节点进行大堆化}for(i=len-1;i>0;i--){swap(&arr[0],&arr[i]); //交换第一个和最后一个元素re_heap(arr,0,i); //对第一个元素进行大堆化}
}
8.快速排序
思路:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
过程:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
- 时间复杂度:O(nlog2n)
- 稳定性:不稳定的算法
- 代码实现:
void quick_sort(int arr[],size_t left,size_t right)
{if(left>=right){ //如果只有一个元素,那就是有序的,返回return; }int i = left;int j = right;int key = arr[left]; //基准值while(i<j){ //找到基准值的位置,使得基准值右边的元素都比基准值大,左边的元素都比基准值小while(i<j&&arr[j]>=key){ //从右边找一个比基准值小的数,--j;}arr[i] = arr[j];//把这个值放到基准值的位置处while(i<j&&arr[i]<=key){ //从左边找一个比基准值大的数++i; }arr[j] = arr[i]; //把这个元素放到j的位置}arr[i] = key;if(i-left>1) //元素个数至少两个才进行递归调用,这样可以少一次递归quick_sort(arr,left,i-1); //对基准值左边的元素进行排序if(right-i>1)quick_sort(arr,i+1,right); //对基准值右边的元素进行排序
}
9.归并排序
思路:对于两个有序的子序列,可以把它们合并在一起,变成一个新的完全有序的序列,因此归并排序和快排差不多,都是递归的进行。
- 时间复杂度:O(nlog2n)
- 稳定性:稳定的算法
代码实现:
void merge(int arr[],int left,int right)
{int i,j,k;int mid = (left+right)/2;int len = mid-left+1;int *temp = malloc(sizeof(arr[0])*len);for(i=0;i<len;i++){temp[i] = arr[i+left]; //把这个数组的所有元素都复制到临时数组中}i=0,j=mid+1,k=left;while(i<len&&j<=right){if(temp[i]<arr[j]){ //把临时数组的元素和 [mid+1,right]这部分的元素一个一个的进行比较,如果谁小,那么arr里就存放谁的元素arr[k++] = temp[i++]; }else{arr[k++] = arr[j++]; }}while(i<len){ //如果temp这个数组的元素还没有全部遍历完,那就把temp后面的元素都复制到arr里面去,//因为arr[mid+1,right] 这部分的元素本来就是arr后面部分的有序的元素,所以如果arr[mid+1,right]这部分没有遍历完也没关系的,arr[k++] = temp[i++]; }free(temp);
}
void merge_sort(int arr[],int left,int right)
{if(left>=right){ //如果只有一个元素说明这个序列有序,那就返回return; } int mid = (left+right)/2; //对两个有序的数组进行排序,merge_sort(arr,left,mid); //对[left,mid]这个区间的元素进行排序merge_sort(arr,mid+1,right); //对[mid+1,right]这个区间内的元素进行排序merge(arr,left,right); //这个序列的[left,mid]为有序的序列 [mid+1,right]也为有序的序列
}
10.计数排序
思路:这是一种基于比较的算法,我们用一个大数组来存放这些数据,这些数据在这个大数组中的表现形式是以这个大数组的下标存在的,比如57,60,42这三个数字进行排序,那么用一个大数组,这个大数组的arr[57] = 1,arr[60] = 1,arr[42] = 1,然后遍历这个大数组就行了。
- 时间复杂度:O(n+k),其中这个k为数据的范围,所以计数排序最适合数据比较集中的数组排序。
- 稳定性:稳定的算法
- 代码实现:
void count_sort(int arr[],size_t len)
{int max = arr[0]; //最大值int min = arr[0]; //最小值size_t i;for(i=0;i<len;i++){if(max<arr[i]){ //找到最大值max =arr[i]; }if(min > arr[i]){ //找到最小值min = arr[i]; }}int cnt = max-min+1; //范围int *prr = malloc(cnt*sizeof(int)); //申请临时空间for(i=0;i<cnt;i++){ //这个临时数组全部置0prr[i] = 0; }for(i=0;i<len;i++){ //对需要进行排序的序列进行遍历prr[arr[i]-min]++; //让下标为(arr[i]-min)的临时大数组的值+1}size_t j=0;for(i=0;i<cnt;i++){ //遍历这个临时数组while(prr[i]){ //如果这个数组下标为i的值不等于0arr[j++] = i+min; //那就让需要进行排序的数组的值为i+min;--prr[i];} }free(prr); //释放掉申请的动态内存
}
11.桶排序
思路:工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。
这是一种以消耗大量空间来换取高效率的排序方式,
- 时间复杂度:O(N+C),其中C=N*(logN-logM),M为桶的数量。所以对于桶排序,桶的数量越多,其排序效率越高。
- 稳定性:稳定的算法
代码实现:
首先定义桶这个类型:
typedef struct Bucket
{int vect[100]; //其实这里使用链表更好,但是我比较懒,就懒得用链表了int cnt; //当前桶内存放数据的个数
}Bucket;void bucket_sort(int arr[],size_t len)
{int min = arr[0];int max = arr[0];size_t i;for(i=0;i<len;i++){if(min>arr[i]){ //找到最小值min = arr[i]; }if(max<arr[i]){ //找到最大值max = arr[i]; }}int size = max-min+1;Bucket bucket[5] = {}; //其实桶可以动态规划,但为了方便我这里直接分为5个桶for(i=0;i<len;i++){ //遍历待排序的数组,把每个元素放到相应的桶当中,//比如[0,200]之间的元素放到下标为0的桶中,[201,400]之间的元素放到下标为1的桶中..//以此类推,直到放完所有的数据int index = (arr[i]-min)/(size/5); //用来判断当前元素arr[i]需要放到哪个桶当中bucket[index].vect[bucket[index].cnt++] = arr[i];}size_t j=0,k=0;for(i=0;i<5;i++){ //对这五个桶进行遍历count_sort(bucket[i].vect,bucket[i].cnt); //首先对这个桶内的元素进行排序,//这里可以调用其他排序方法,也可以递归调用当前排序方法,但是为了节省内存,我选择调用其他排序方法,for(j=0;j<bucket[i].cnt;j++){arr[k++] = bucket[i].vect[j]; //对排序好的桶进行遍历,并且把里面的元素复制到arr中去 }}
}
12.基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog®m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
解法:
1.首先根据个位数的数值,在走访数值时将它们分配至编号0到9的桶子中;
2.接下来将这些桶子中的数值重新串接起来,接着再进行一次分配,这次是根据十位数来分配;
3.接下来将这些桶子中的数值重新串接起来,持续进行以上的动作直至最高位数为止。
- 时间复杂度:设待排序列为n个记录,d个关键码,关键码的取值范围为radix,则进行链式基数排序的时间复杂度为O(d(n+radix)),其中,一趟分配时间复杂度为O(n),一趟收集时间复杂度为O(radix),共进行d趟分配和收集。
- 稳定性:稳定的算法;
代码实现:
还是定义桶的类型:
typedef struct Bucket{int vect[100]; //同样的可以用链表int cnt;
}Bucket;void base_sort(int arr[],size_t len)
{size_t i;Bucket bucket[10] = {}; //十个桶int max = arr[0];for(i=0;i<len;i++){ //寻找最大值,就可以判断最大值的位数if(arr[i]>max){max = arr[i]; } }size_t j,k;int num = 1; //用来获得相应位数上的数字的关键参数,//比如要获得个位上的参数时num = 1;//获得十位上的数字时num = 10;//以此类推do{for(i=0;i<len;i++){ //遍历待排序的数组,把每个元素放入相应的桶中//比如251,当获得个位上的数字时,251放到下标为1的桶当中//当获得十位上的数字时,251放到下标为5的桶当中//当获得百位上的数字时,251放到下标为2的桶当中//当获得千位上的数字时,251放到下标为0的桶当中//以此类推int index = arr[i]/num%10; //获得相应位数上的数字bucket[index].vect[bucket[index].cnt++] = arr[i]; //把这个数字放到相应的桶中}k=0;for(i=0;i<10;i++){for(j=0;j<bucket[i].cnt;j++){arr[k++] = bucket[i].vect[j]; //把这些桶按顺序依次遍历,//把桶中的元素重新放回arr当中} bucket[i].cnt = 0; //记得让桶中的cnt变为0,方便下一次存放}num*=10; //num*10}while(max/=10);//循环条件
}
=========以上内容来自:用C语言完整实现12种排序方法_c语言快速排序解决排序问题-CSDN博客============

相关文章:

C语言实现12种排序算法
1.冒泡排序 思路:比较相邻的两个数字,如果前一个数字大,那么就交换两个数字,直到有序。 时间复杂度:O(n^2),稳定性:这是一种稳定的算法。 代码实现: void bubble_sort(int arr[],…...

C语言应用实例——贪吃蛇
(图片由AI生成) 0.贪吃蛇游戏背景 贪吃蛇游戏,最早可以追溯到1976年的“Blockade”游戏,是电子游戏历史上的一个经典。在这款游戏中,玩家操作一个不断增长的蛇,目标是吃掉出现在屏幕上的食物,…...

Mac如何设置一位数密码?
一、问题 Mac如何设置一位数密码? 二、解答 1、打开终端 2、清除全局账户策略 sudo pwpolicy -clearaccountpolicies 输入开机密码,这里是看不见的,输入完回车即可 3、重新设置密码 (1)打开设置-->用户和群组…...

运动编辑学习笔记
目录 跳舞重建: 深度运动重定向 Motion Preprocessing Tool anim_utils MotionBuilder 跳舞重建: https://github.com/Shimingyi/MotioNet 深度运动重定向 https://github.com/DeepMotionEditing/deep-motion-editin 游锋生/deep-motion-editin…...
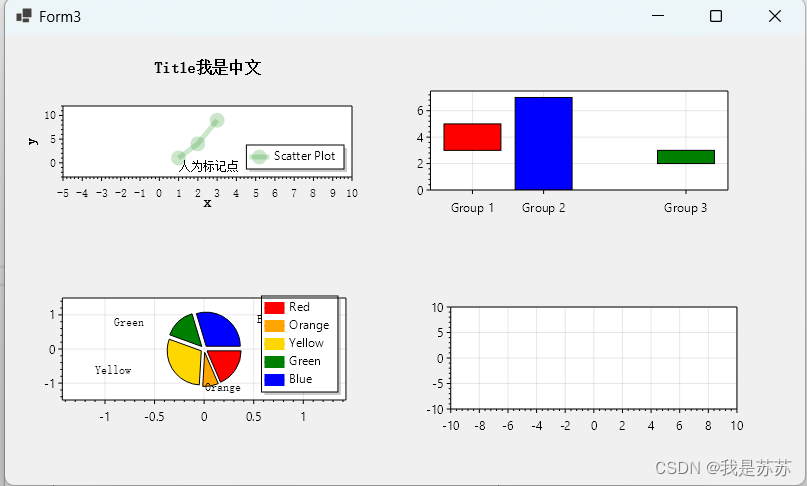
C#小结:ScottPlot 5.0在VS2022桌面开发的应用(以winform为例)
目录 一、官网文档地址 二、在VS2022中安装Scottplot 三、拖动Scottplot 四、使用Scottplot 五、效果图 一、官网文档地址 官网地址:ScottPlot 5.0 食谱 本文内容来自于官网,选取了官网的一些比较好用的功能展示,如需学习更多功能&a…...

Jmeter性能测试: Jmeter 5.6.3 分布式部署
目录 一、实验 1.环境 2.jmeter 配置 slave 代理压测机 3.jmeter配置master控制器压测机 4.启动slave从节点检查 5.启动master主节点检查 6.运行jmeter 7.观察jmeter-server主从节点变化 二、问题 1.jmeter 中间请求和响应乱码 一、实验 1.环境 (1&#…...

跟着cherno手搓游戏引擎【15】DrawCall的封装
目标: Application.cpp:把渲染循环里的glad代码封装成自己的类: #include"ytpch.h" #include "Application.h"#include"Log.h" #include "YOTO/Renderer/Renderer.h" #include"Input.h"namespace YO…...
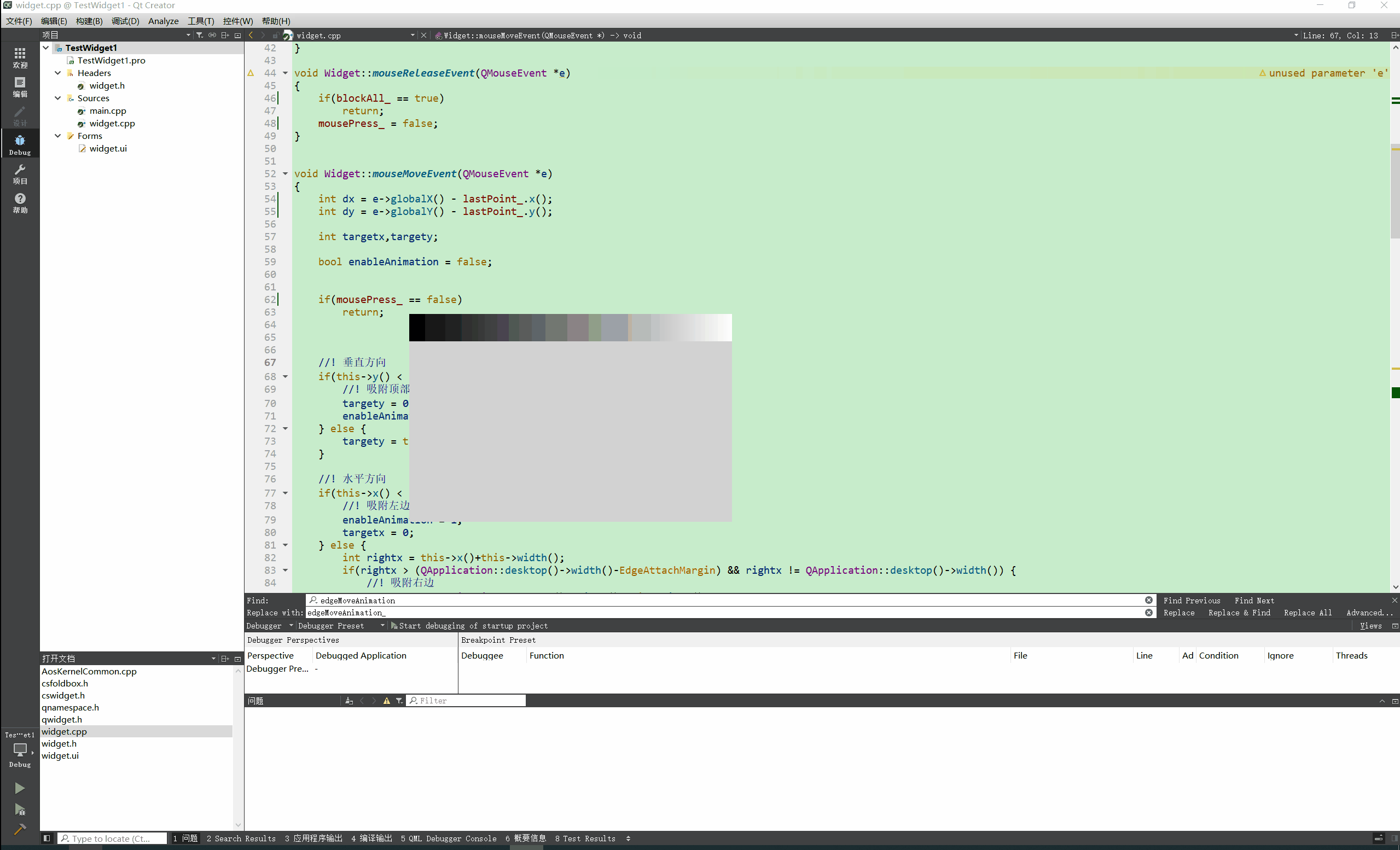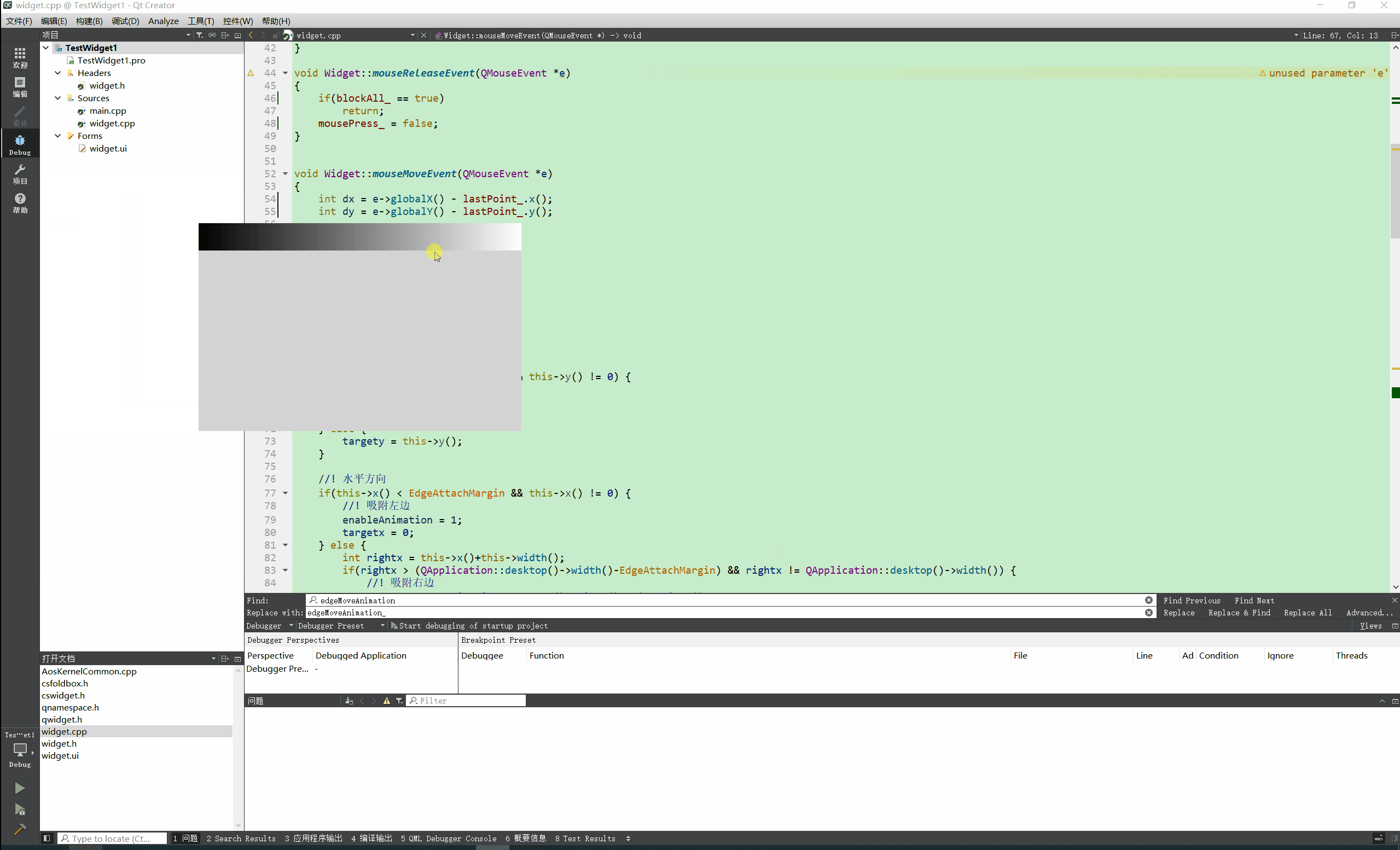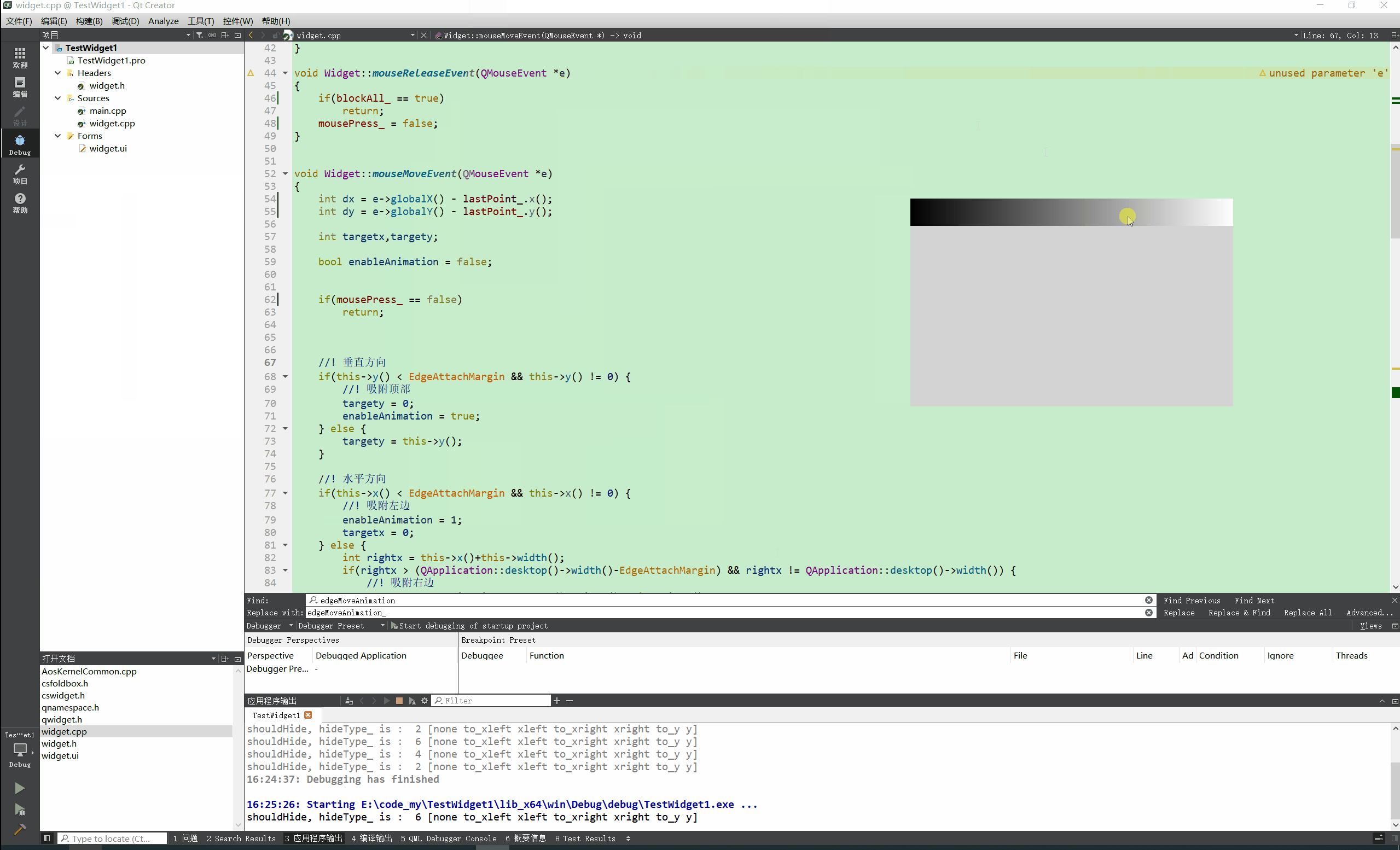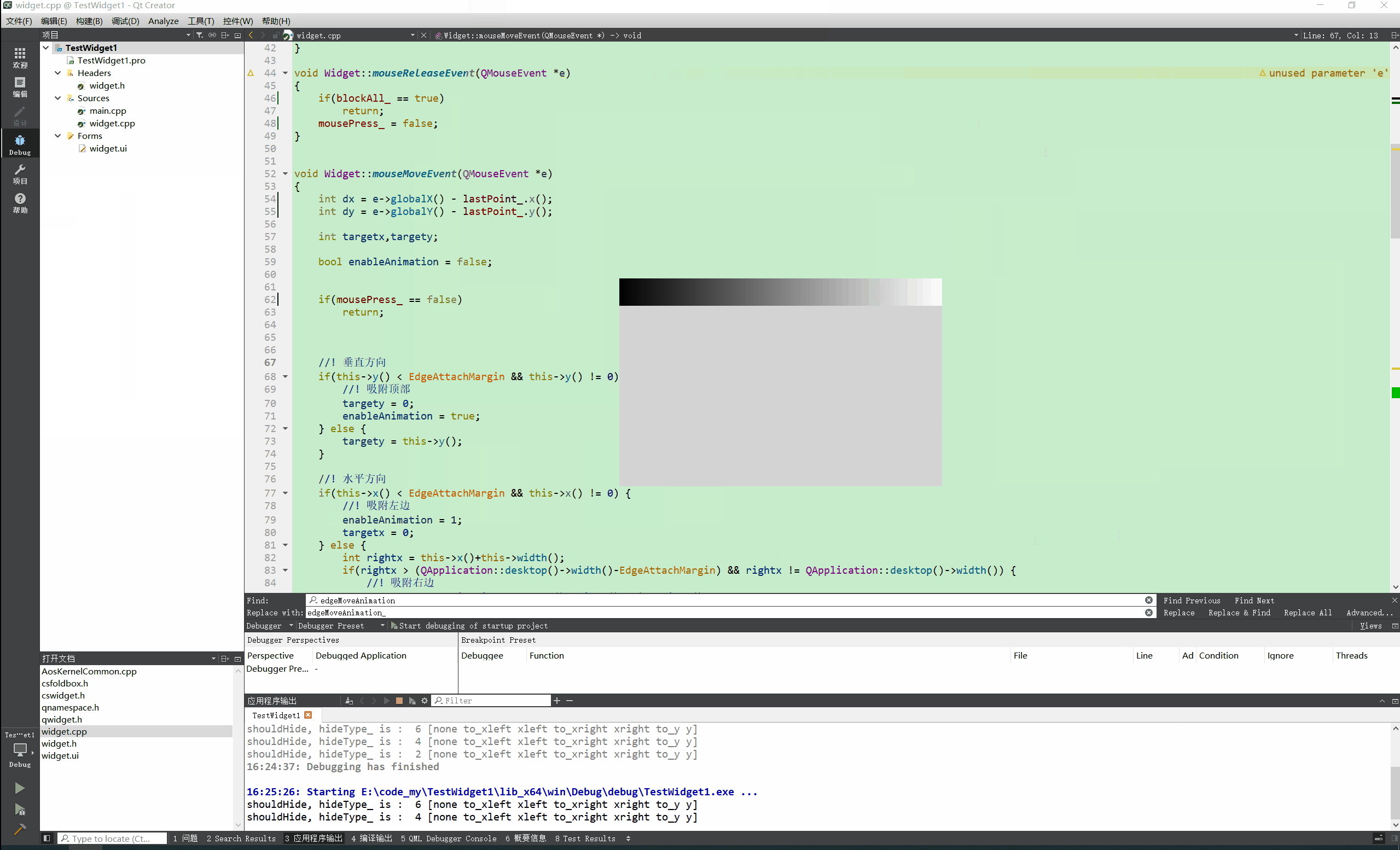
Qt实现窗口吸附屏幕边缘 自动收缩
先看效果: N年前的QQ就可以吸附到屏幕边缘,聊天时候非常方便,不用点击状态栏图标即可呼出QQ界面 自己尝试做了一个糙版的屏幕吸附效果。 关键代码: void Widget::mouseMoveEvent(QMouseEvent *e) {int dx e->globalX() - l…...
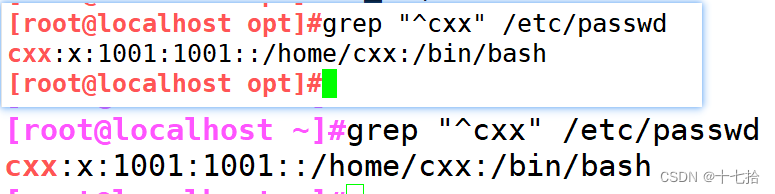
shell脚本之免交互
目录 一、Here Document 免交互 1、交互与免交互的概念 2、 Here Document 概述 二、Here Document 应用 1、使用cat命令多行重定向 2、使用tee命令多行重定向 3、使用read命令多行重定向 4、使用wc -l统计行数 5、使用passwd命令用户修改密码 6、Here Document 变量…...
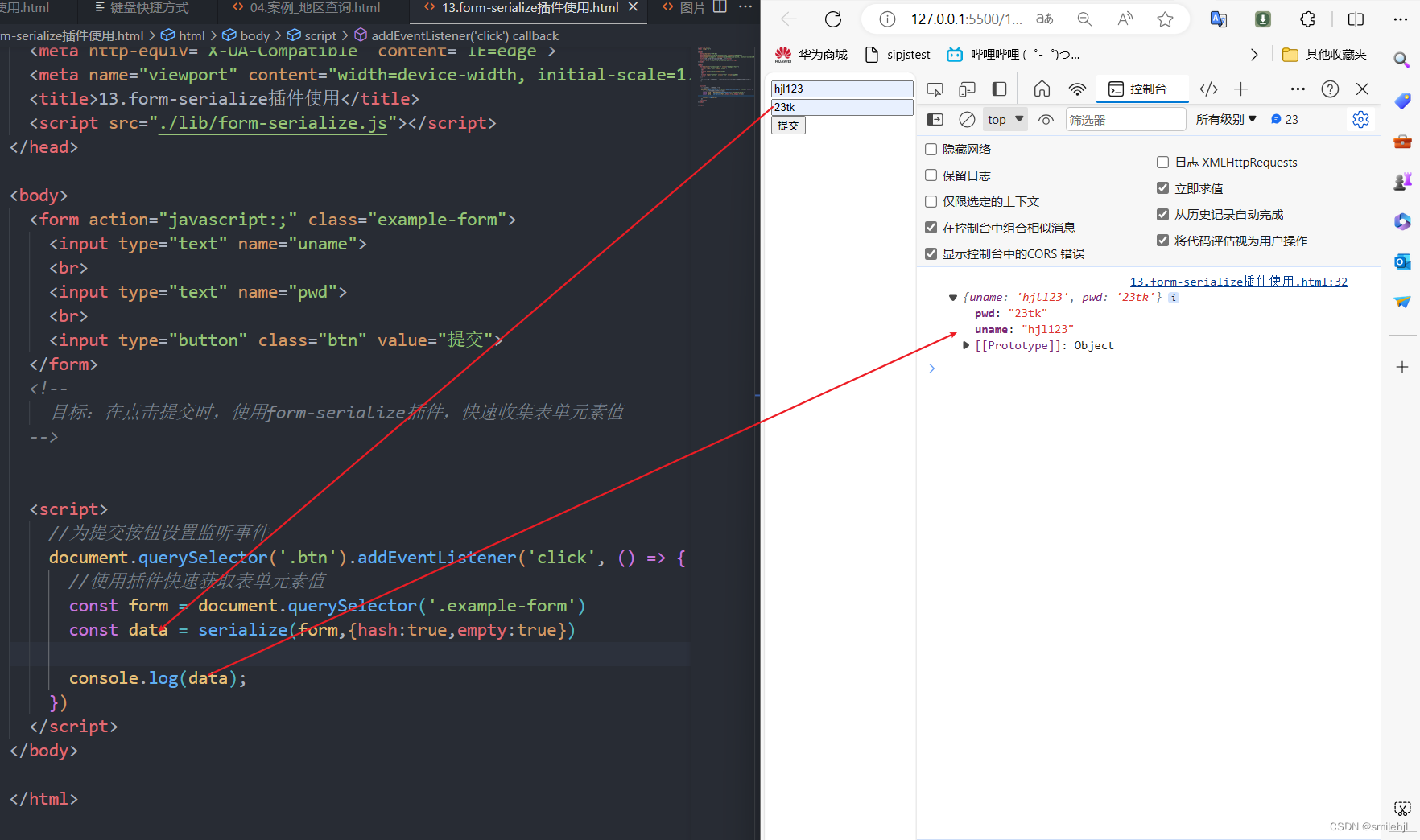
Ajax入门与使用
目录 ◆ AJAX 概念和 axios 使用 什么是 AJAX? 怎么发送 AJAX 请求? 如何使用axios axios 函数的基本结构 axios 函数的使用场景 1 没有参数的情况 2 使用params参数传参的情况 3 使用data参数来处理请求体的数据 4 上传图片等二进制的情况…...
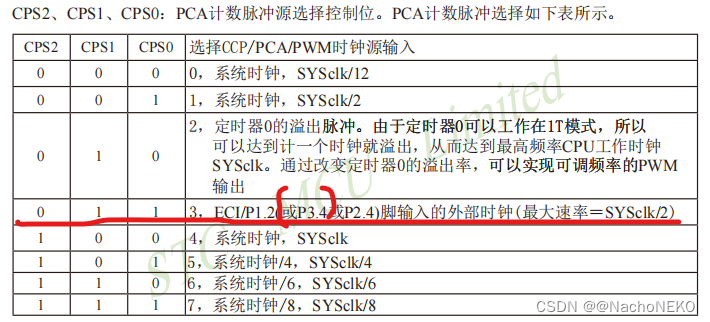
蓝桥杯备战——11.NE555测频
1.分析原理图 我们可以看到,上图就是一个NE555构建的方波发生电路,输出方波频率1.44/2(R8Rb3)C,如果有不懂NE555内部结构,工作原理的,可以到B站学习。实在不懂仿真也行,比如我下面就是仿真结果: 然后就是下…...

代码随想录算法训练营第三十三天|509. 斐波那契数 ,● 70. 爬楼梯 , 746. 使用最小花费爬楼梯
确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 代码随想录 视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩…...

Node.js 文件系统操作指南
文章目录 Node.js 文件系统操作完全指南一、引言二、基本文件操作2.1 读取文件2.2 写入文件2.3 追加内容到文件 三、文件与目录的创建与删除3.1 创建文件3.2 创建目录3.3 删除文件3.4 删除目录 四、文件与目录的信息查询4.1 检查文件或目录是否存在4.2 获取文件信息4.3 获取目录…...

Kotlin 协程1:深入理解withContext
Kotlin 协程1:深入理解withContext 引言 在现代编程中,异步编程已经变得非常重要。在 Kotlin 中,协程提供了一种优雅和高效的方式来处理异步编程和并发。在这篇文章中,我们将深入探讨 Kotlin 协程中的一个重要函数:wi…...
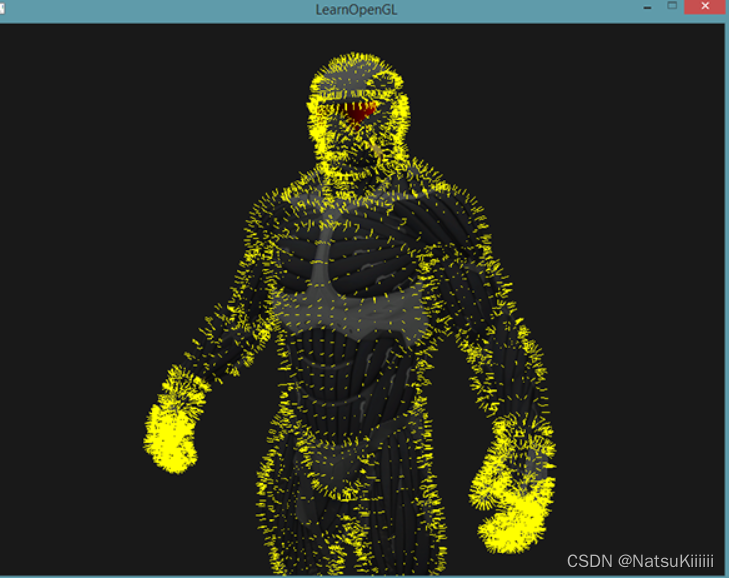
(自用)learnOpenGL学习总结-高级OpenGL-几何着色器
在顶点着色器和片段着色器中间还有一个几何着色器。 几何着色器的输入是一个图元的一组顶点,在几何着色器中进行任意变换之后再给片段着色器,可以变成完全不一样的图元、可以生成更多的顶点。 #version 330 core layout (points) in; layout (line_str…...
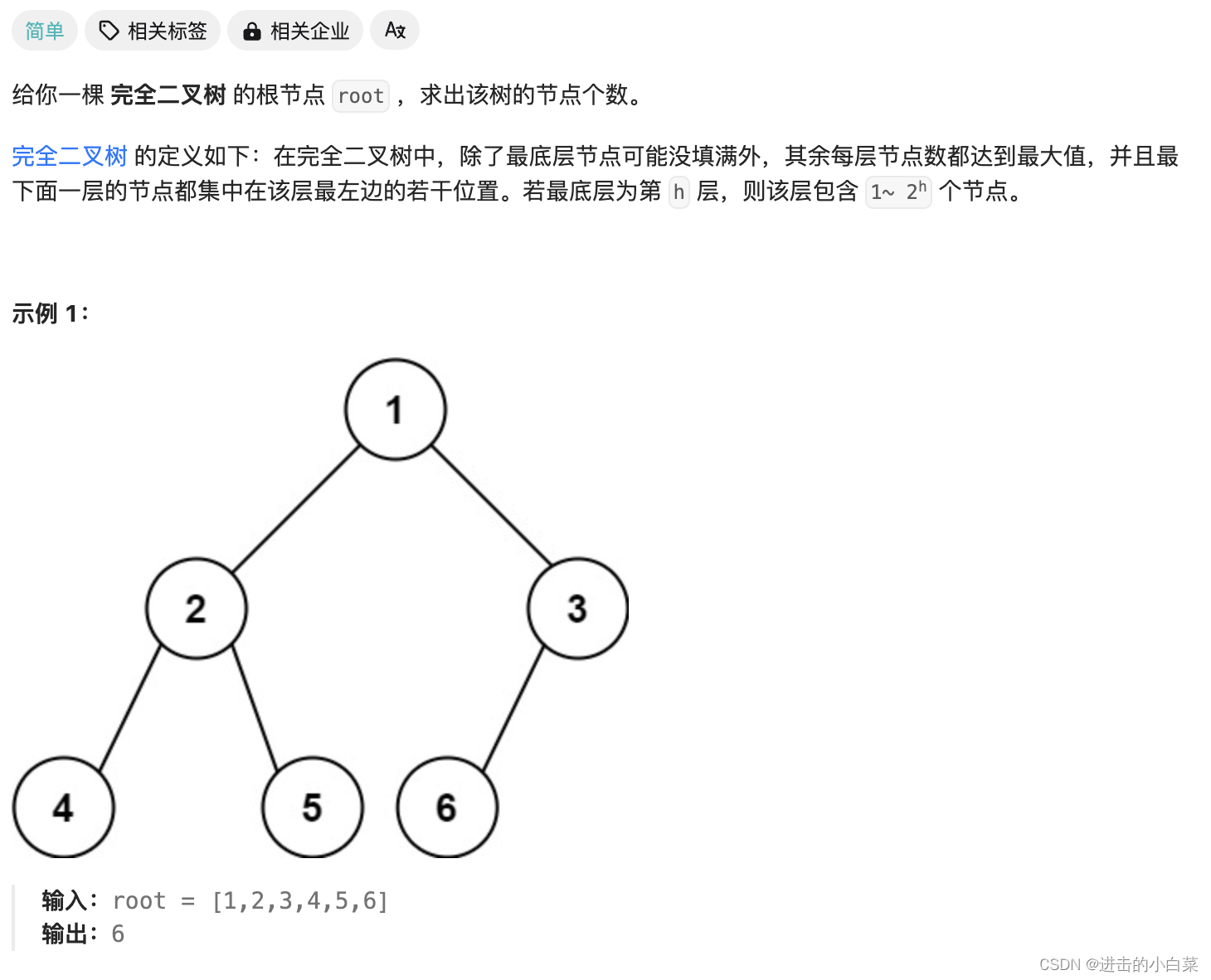
坚持刷题 | 完全二叉树的节点个数
Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数 题目 222.完全二叉树的节点个数 代码实现 class TreeNode {int val;TreeNode left, right;public TreeNode(int val) …...

K8S网络
一、介绍 k8s不提供网络通信,提供了CNI接口(Container Network Interface,容器网络接口),由CNI插件实现完成。 1.1 Pod通信 1.1.1 同一节点Pod通信 Pod通过虚拟Ethernet接口对(Veth Pair)与外部通信,Veth…...

【蓝桥杯51单片机入门记录】LED
目录 一、基础 (1)新建工程 (2)编写前准备 二、LED (1)点亮LED灯 (2)LED闪烁 延时函数的生成(stc-isp中生成) 实现 (3)流水灯…...
)
轻松使用python将PDF转换为图片(成功)
使用PyMuPDF(fitz)将PDF转换为图片 在处理PDF文件时,我们经常需要将PDF页面转换为图片格式,以便于在网页、文档或应用程序中显示。Python提供了多种方式来实现这一需求,本文将介绍如何使用PyMuPDF(也称为f…...

【目标检测】对DETR的简单理解
【目标检测】对DETR的简单理解 文章目录 【目标检测】对DETR的简单理解1. Abs2. Intro3. Method3.1 模型结构3.2 Loss 4. Exp5. Discussion5.1 二分匹配5.2 注意力机制5.3 方法存在的问题 6. Conclusion参考 1. Abs 两句话概括: 第一个真正意义上的端到端检测器最…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
