CodeForce 455A. Boredom
题目链接
CodeForce 455A. Boredom
思路
因为跟序列的下标无关,所以先对数组a排个序。那么每次选择只会影响两侧的元素。
记号
令dp[i]dp[i]dp[i]表示排序后a[1..i]a[1..i]a[1..i]能够获得的最大点数。
但是这样不足以区分是否当前元素可以被使用,所以再开一个维度,
令:
dp[i][0]dp[i][0]dp[i][0]表示我们无法使用当前元素a[i]a[i]a[i]所获得的最大点数。
dp[i][1]dp[i][1]dp[i][1]表示我们使用当前元素a[i]a[i]a[i]能够获得的最大点数。
那么对相邻的两个元素讨论即可。
状态转移方程
对于a[i] > a[i-1] + 1,
那么当前选择不会影响到之前的点数。所以
dp[i][1]=max(dp[i−1][0],dp[i−1][1])+a[i]dp[i][1] = max(dp[i-1][0],dp[i-1][1]) + a[i]dp[i][1]=max(dp[i−1][0],dp[i−1][1])+a[i]
对于a[i] == a[i-1]+1,
- 若此时选择a[i],则与a[i-1]相等的都不能被选中。j是最大满足a[j] < a[i-1]的下标j,那么dp[i][1]=dp[j]+a[i]dp[i][1] = dp[j] + a[i]dp[i][1]=dp[j]+a[i]
- 若此时不选择a[i],那么当然得选择a[i-1]才会更好。故dp[i][0]=dp[i−1][1]dp[i][0]=dp[i-1][1]dp[i][0]=dp[i−1][1]
对于a[i] == a[i-1],那么当a[i-1]不能被选择时,a[i]也不能被选择。反之亦然。
故有dp[i][0]=dp[i−1][0]dp[i][1]=dp[i−1][1]+a[i]dp[i][0]=dp[i-1][0] \\dp[i][1] = dp[i-1][1] + a[i] dp[i][0]=dp[i−1][0]dp[i][1]=dp[i−1][1]+a[i]
代码
#include<bits/stdc++.h>using namespace std;typedef long long LL;
vector<LL> a;int main() {int n;cin >> n;a.resize(n + 1);for (int i = 1; i <= n; ++i) {cin >> a[i];}sort(a.begin() + 1, a.end());vector<vector<LL>> dp(n + 1, vector<LL>(2));dp[1][1] = a[1];for (int i = 2; i <= n; ++i) {if (a[i] > a[i - 1] + 1) {// dp[i][1]表示使用了当前元素dp[i][1] = max(dp[i - 1][0], dp[i - 1][1]) + a[i];} else {if (a[i] == a[i - 1] + 1) {// the prev of first element equal to a[i-1]int j = lower_bound(a.begin() + 1, a.begin() + i, a[i - 1]) - a.begin() - 1;dp[i][1] = max(dp[j][1], dp[j][0]) + a[i];dp[i][0] = dp[i - 1][1];} else if (a[i] == a[i - 1]) {dp[i][0] = dp[i - 1][0];dp[i][1] = dp[i - 1][1] + a[i];}}
// printf("dp[%d]=%d\n", i, max(dp[i][0], dp[i][1]));}cout << max(dp[n][0], dp[n][1]);
}
相关文章:

CodeForce 455A. Boredom
题目链接 CodeForce 455A. Boredom 思路 因为跟序列的下标无关,所以先对数组a排个序。那么每次选择只会影响两侧的元素。 记号 令dp[i]dp[i]dp[i]表示排序后a[1..i]a[1..i]a[1..i]能够获得的最大点数。 但是这样不足以区分是否当前元素可以被使用,所…...

geoserver之BlobStores使用
概述 geoserver是常用的地图服务器之一,除了基本的能力之外,也提供了很多的插件方便大家使用。在本文,讲述一下如何在geoserver中使用BlobStores和gwc-sqlite-plugin插件实现地图的切片和部署。 BlobStores简介 在geoserver中,…...

跨域问题以及Ajax和Axios的区别
文章目录1. 同源策略2. 同源策略案例3. 什么是跨域4. 跨域解决方法4.1 Ajax的jsonp4.2 CORS方式4.3 Nginx 反向代理5. Axios 和 Ajax 的区别6. Axios 和 Ajax 的区别及优缺点6.1 Ajax:6.1.1 什么是Ajax6.1.2 Ajax的原理6.1.3 核心对象6.1.4 Ajax优缺点6.1.4.1 优点&…...
现代卷积神经网络(AlexNet)
专栏:神经网络复现目录 本章介绍的是现代神经网络的结构和复现,包括深度卷积神经网络(AlexNet),VGG,NiN,GoogleNet,残差网络(ResNet),稠密连接网络…...
单向非循环链表
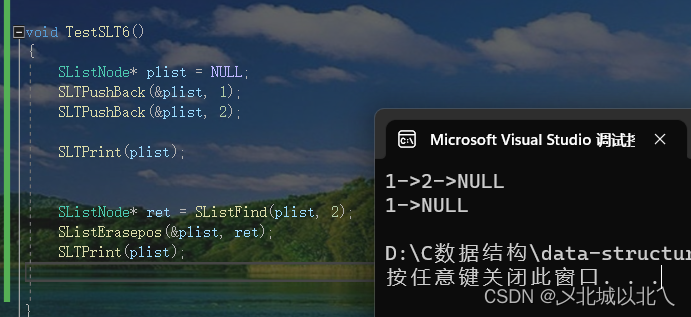
1、顺序表遗留问题 1. 中间/头部的插入删除,时间复杂度为O(N) 2. 增容需要申请新空间,使用malloc、realloc等函数拷贝数据,释放旧空间。会有不小的消耗。 3. 当我们以2倍速度增容时,势必会有一定的空间浪费。例如当前容量为100&a…...

Vue2的基本内容(一)
目录 一、插值语法 二、数据绑定 1.单向数据绑定 2.双向数据绑定 三、事件处理 1.绑定监听 2.事件修饰符 四、计算属性computed和监视属性watch 1.计算属性-computed 2.监视属性-watch (1)通过 watch 监听 msg 数据的变化 (2&a…...

蚁群算法优化最优值
%%%%%%%%%%%%%%蚁群算法求函数极值%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%% clear all; %清除所有变量 close all; %清图 clc; %清屏 m 20; %蚂蚁个数 G 500; %最大迭代次数 Rho 0.9; %信息素蒸发系数 P0 0.2; %转移概率常数 XMAX 5; %搜索变量 x…...

Docker镜像的内部机制
Docker镜像的内部机制 镜像就是一个打包文件,里面包含了应用程序还有它运行所依赖的环境,例如文件系统、环境变量、配置参数等等。 环境变量、配置参数这些东西还是比较简单的,随便用一个 manifest 清单就可以管理,真正麻烦的是文…...
每日的时间安排规划
14:23 2023年3月4日星期六 开始 现在我要做一套试卷。模拟6级考试。 现在是: 16:22 2023年3月4日星期六。 做完了线上的试卷! 发现我真的是不太聪明的样子! 明明买的有历年真题,做真题就行了,还要做它们出的模拟的…...
【C++】类和对象——六大默认成员函数
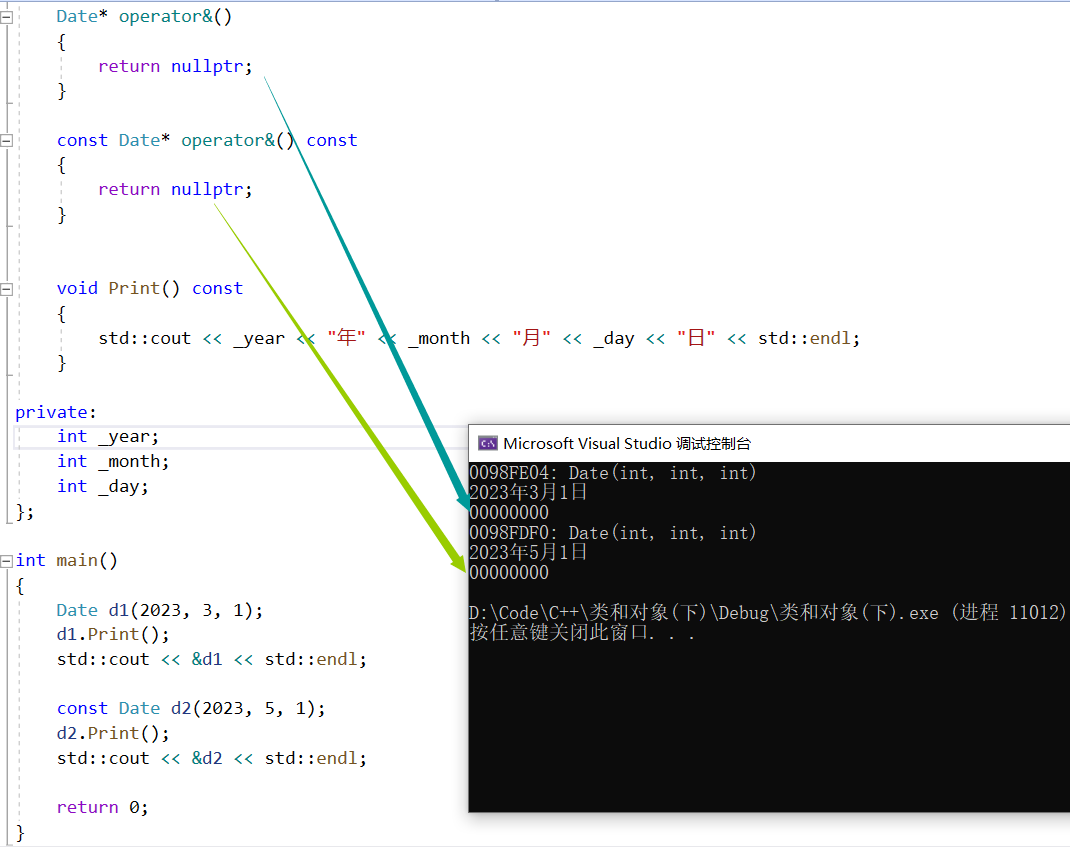
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录前言一、类的6个默认成员函数二、构造…...

远程debug被arthas watch了的idea
开发工具idea端(2021.2.1) 远程调试 被 应用了 修改的arthas端 的 鸡idea端(2022.3.2) A. 鸡idea端 鸡idea: “D:\IntelliJ IDEA 2022.3.2\bin\idea64.exe” 中安装有目标插件 比如 RedisNew-2022.07.24.zip 对文件 “D:\IntelliJ IDEA 2022.3.2\bin\idea64.exe.vmoptions” 新…...
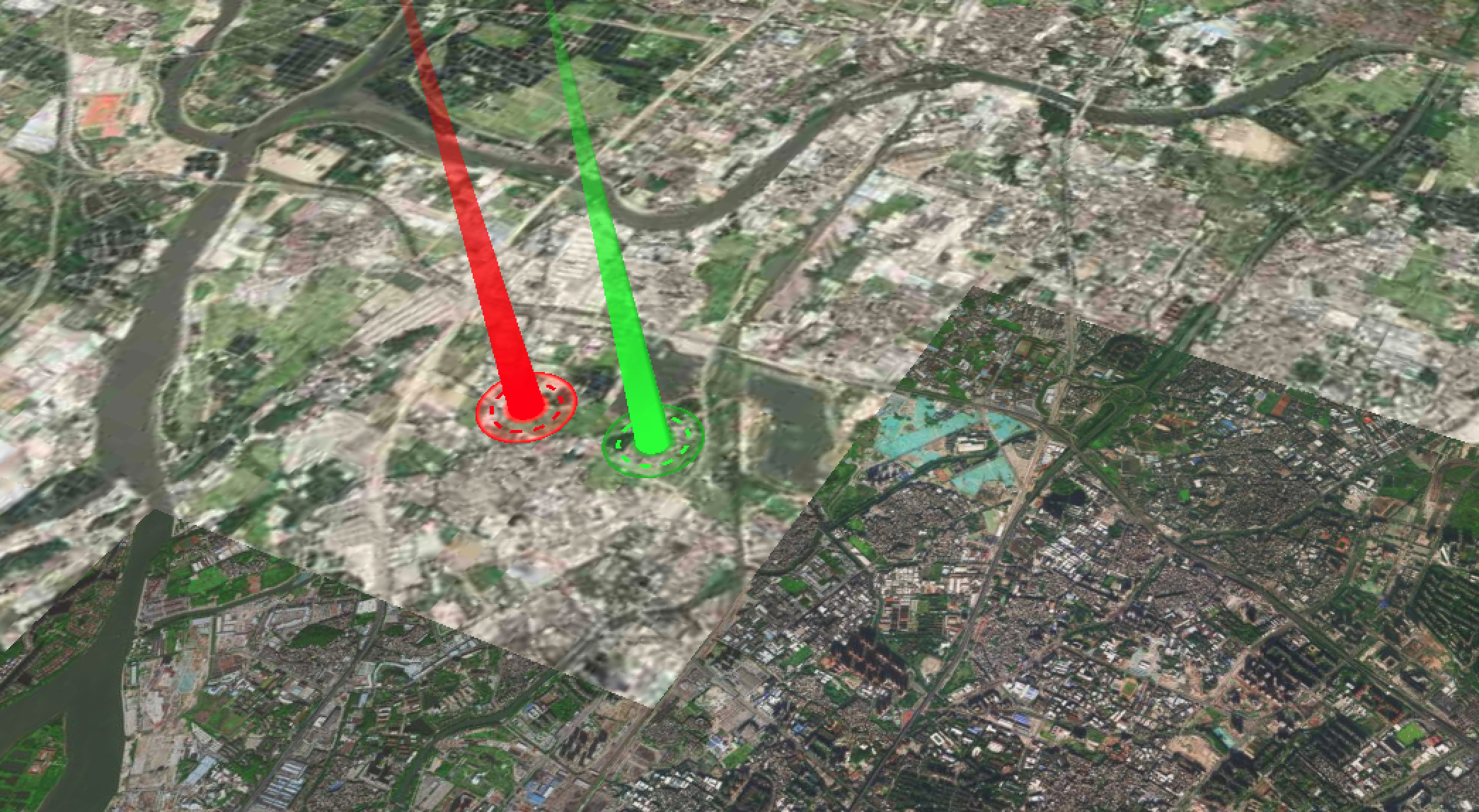
Cesium实现的光柱效果
Cesium实现的光柱效果 效果展示: 可以通过拼接两个entity来实现这个效果: 全部代码; index.html <!DOCTYPE html> <html><head><meta charset...
和splice())
你最爱记混的slice()和splice()
slice()方法:选取数组的一部分,并返回一个新数组 该方法不会改变原始数组,而是将截取到的元素封装到一个新数组中返回 语法:array.slice(start,end),参数的介绍如下: 语法:array.slice(start,end),参数的介绍如下: 1.start:截取开始的位置的索引,包含开始索引 2.…...

【LeetCode】剑指 Offer(15)
目录 题目:剑指 Offer 32 - II. 从上到下打印二叉树 II - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 32 - III. 从上到下打…...

【刷题笔记】之二分查找(搜索插入位置。在排序数组中查找元素的第一个和最后一个位置、x的平方根、有效的完全平方数)
1. 二分查找题目链接 704. 二分查找 - 力扣(LeetCode)给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -…...
)
一起Talk Android吧(第五百一十五回:绘制向外扩散的水波纹)
文章目录整体思路实现方法示例代码各位看官们大家好,上一回中咱们说的例子是"Java中的进制转换",这一回中咱们说的例子是"绘制向外扩散的水波纹"。闲话休提,言归正转, 让我们一起Talk Android吧! 整体思路 …...

基于粒子群改进的支持向量机SVM的情感分类识别,pso-svm情感分类识别
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于SVM的情感分类预测 代码 结果分析 展望 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型…...
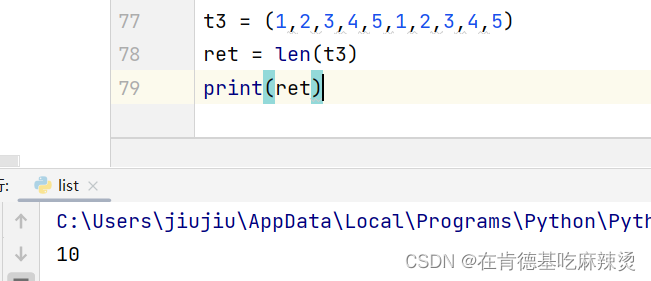
【python中的列表和元组】
文章目录前言一、列表及其使用1.列表的特点2. 列表的使用方法二、元组及其特点1.元组的类型是tuple1.元组的查找操作2. 计算元组某个元素出现的次数3.统计元组内元素的个数总结前言 本文着重介绍python中的列表和元组以及列表和元组之间的区别 一、列表及其使用 1.列表的特点…...

世界顶级五大女程序媛,不仅技术强还都是美女
文章目录1.计算机程序创始人:勒芙蕾丝伯爵夫人2.首位获得图灵奖的女性:法兰艾伦3.谷歌经典首页守护神:玛丽莎梅耶尔4.COBOL之母:葛丽丝穆雷霍普5.史上最强游戏程序媛-余国荔说起程序员的话,人们想到的都会是哪些理工科…...
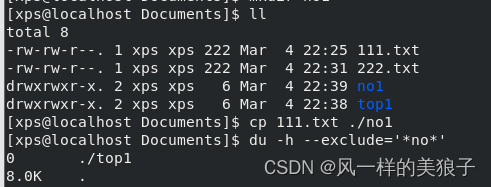
Linux- 系统随你玩之--文件管理-双生姐妹花
文章目录1、前言2、文件管理-双生姐妹花2.1、 df2.1.1、 df 语法2.1.1 、常用参数2.2、 du2.2.1、du 语法2.1.1、 常用参数2.3、双生姐妹花区别2.3.1、 查看文件统计 的计算方式不同2.3.2 、删除文件情况下统计结果 不同2.3.3 、针对双生姐妹花区别 结语3、双生姐妹花实操3.1 、…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
