机器学习5-线性回归之损失函数
在线性回归中,我们通常使用最小二乘法(Ordinary Least Squares, OLS)来求解损失函数。线性回归的目标是找到一条直线,使得预测值与实际值的平方差最小化。
假设有数据集
其中
是输入特征,
是对应的输出。
线性回归的模型假设是:
其中, 是输入特征,
是模型的参数。
损失函数(成本函数)表示预测值与实际值之间的差异。对于线性回归,损失函数通常采用均方误差(Mean Squared Error, MSE):
其中 是数据集中的样本数量。
求解损失函数的过程就是找到能够使损失函数最小化的模型参数 。我们通过最小化损失函数来找到最优的参数。这可以通过梯度下降等优化算法来实现。梯度下降的步骤如下:
1. 初始化参数:选择一组初始参数 .
2. 计算梯度:计算损失函数对每个参数的偏导数。
3. 更新参数:使用梯度信息来更新参数,减小损失函数值。
4. 重复步骤2和步骤3:直到收敛或达到预定的迭代次数。
对于线性回归的梯度下降算法,参数的更新规则为:
其中 是学习率,控制每次参数更新的步长。
在具体的计算中,求解偏导数 并代入梯度下降公式进行迭代,直到损失函数收敛到最小值。
下面是对损失函数的偏导数计算过程:
均方误差损失函数:
现在,我们将 展开并对每个
求偏导数。
首先,计算单个样本的损失:
然后,对 对
求偏导数:
现在,我们对 对
求偏导数:
将其代入损失函数的偏导数中:
这就是对于线性回归的均方误差损失函数的偏导数计算过程。在实际应用中,梯度下降算法会根据这些偏导数的信息,迭代更新参数,直至损失函数收敛到最小值。
结论:
以上就是线性回归中求解损失函数的基本过程。这个过程是通过迭代优化算法来找到最优参数,使得模型的预测值与实际值之间的均方误差最小。
相关文章:
机器学习5-线性回归之损失函数
在线性回归中,我们通常使用最小二乘法(Ordinary Least Squares, OLS)来求解损失函数。线性回归的目标是找到一条直线,使得预测值与实际值的平方差最小化。 假设有数据集 其中 是输入特征, 是对应的输出。 线性回归的…...
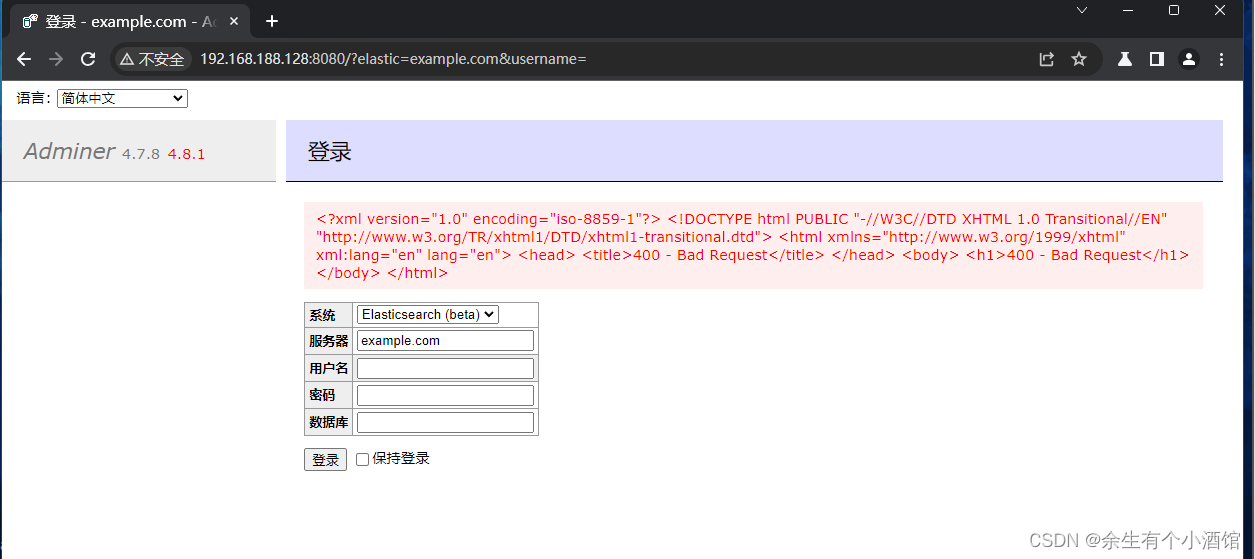
vulhub中Adminer ElasticSearch 和 ClickHouse 错误页面SSRF漏洞复现(CVE-2021-21311)
Adminer是一个PHP编写的开源数据库管理工具,支持MySQL、MariaDB、PostgreSQL、SQLite、MS SQL、Oracle、Elasticsearch、MongoDB等数据库。 在其4.0.0到4.7.9版本之间,连接 ElasticSearch 和 ClickHouse 数据库时存在一处服务端请求伪造漏洞(…...
浅谈Zookeeper及windows下详细安装步骤
1. Zookeeper介绍 1.1 分布式系统面临的问题 分布式系统是一个硬件或软件组件分布在不同的网络计算机上,彼此之间仅仅通过消息传递进行通信和协调的系统。 面临的问题:系统每个节点之间信息同步及共享 以一个小团队为例,面临的问题 通过网络进行信息…...

vite, vue3, vue-router, vuex, ES6学习日记
学习使用vitevue3的所遇问题总结(2024年2月1日) 组件中使用<script>标签忘记加 setup 这会导致Navbar 没有暴露出来,导致使用不了,出现以下报错 这是因为,如果不用setup,就得使用 export default…...

25考研|660/880/1000/1800全年带刷计划
作为一个参加过两次研究生考试的老学姐,我觉得考研数学的难度完全取决于你自己 我自己就是一个很好的例子 21年数学题目是公认的简单,那一年考130的很多,但是我那一年只考了87分。但是22年又都说是有史以来最难的一年,和20年的难度…...

Mybatis基础教程及使用细节
本篇主要对Mybatis基础使用进行总结,包括Mybatis的基础操作,使用注解进行增删改查的练习;详细介绍xml映射文件配置过程并且使用xml映射文件进行动态sql语句进行条件查询;为了简化java开发提高效率,介绍一下依赖&#x…...

10 分钟在K8s 中部署轻量级日志系统 Loki
转载至我的博客 https://www.infrastack.cn ,公众号:架构成长指南 Loki 是什么? Loki是由Grafana Labs开源的一个水平可扩展、高可用性,多租户的日志聚合系统的日志聚合系统。它的设计初衷是为了解决在大规模分布式系统中&#x…...
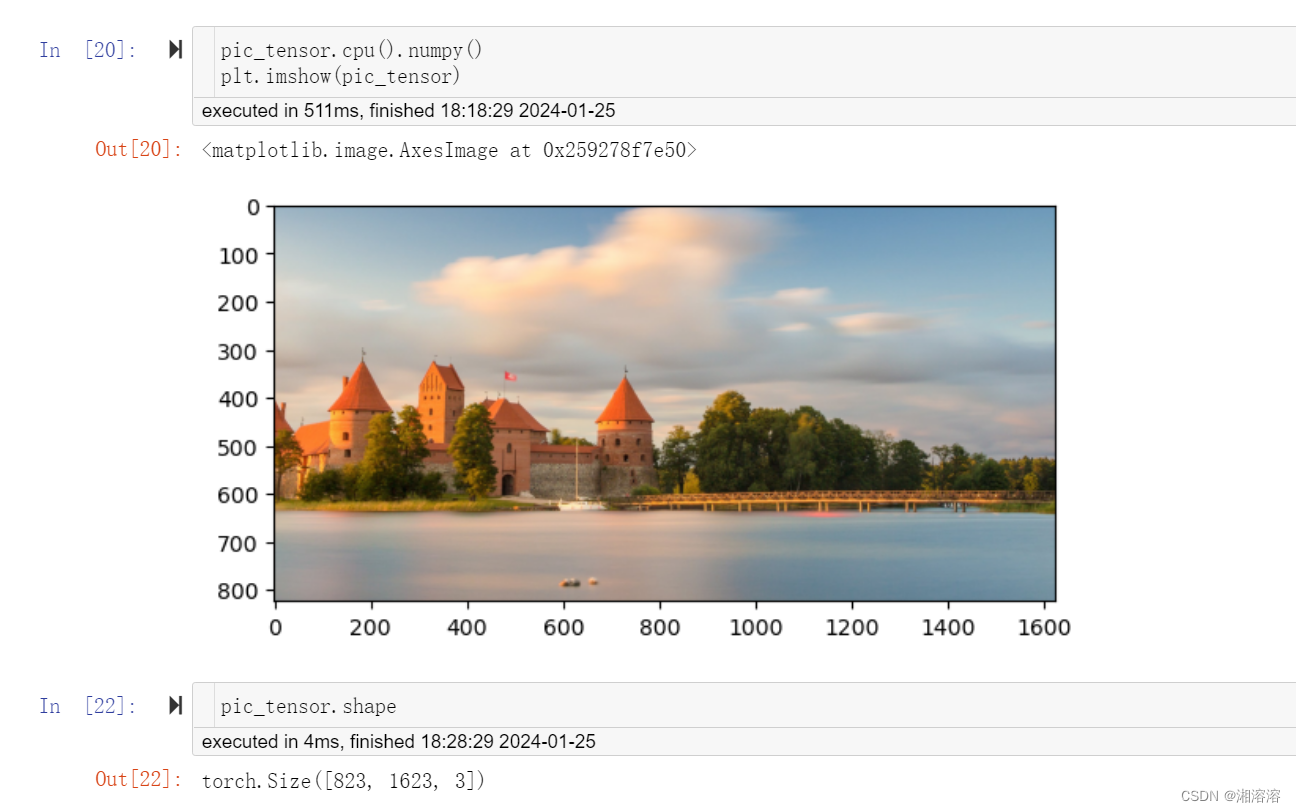
图像处理python基础
array 读取图片 tensor 模型预测 一般过程:读取数据np->tensor->model->result->np->画图 shape确保图像输入输出尺寸正确 读取图片 将在GPU上运行的tensor类型转变成在CPU上运行的np类型 三类计算机视觉任务的输入: 分类࿱…...
基于WordPress开发微信小程序2:决定开发一个wordpress主题
上一篇:基于WordPress开发微信小程序1:搭建Wordpress-CSDN博客 很快发现一个问题,如果使用别人的主题模板,多多少少存在麻烦,所以一咬牙,决定自己开发一个主题模板,并且开源在gitee上ÿ…...

[Python] 什么是网格搜索以及scikit-learn中GridSearch类的介绍和使用案例?
什么是网格搜索? 网格搜索是一种参数调优的方法,它可以帮助找到最佳的模型参数。在网格搜索中,我们先指定参数的候选值范围,然后枚举所有可能的参数组合,计算每个模型的性能指标(比如准确率、精确率等&…...
Linux-正则表达式
1.正则表达式的定义: 正则表达式通常用于判断语句中,使用字符串描述、匹配一系列符合某个规则的字符串。 正则表达式是由普通字符与元字符组成。 普通字符包括小写字母、数字、标点符号及一些其他符号。元字符是指在正则表达式中具有特殊意义的专用字符&…...

Java基础学习:System类和Static方法的实际使用
一、System类 1.在程序开发中,我们需要对这个运行的结果进行检验跟我们预判的结果是否一致,就会用到打印结果在控制台中显示出来使用到了System类。System类定义了一些和系统相关的属性和方法,它的属性和方法都是属于静态的,想使用…...
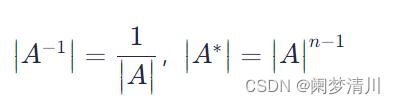
线性代数------矩阵的运算和逆矩阵
矩阵VS行列式 矩阵是一个数表,而行列式是一个具体的数; 矩阵是使用大写字母表示,行列式是使用类似绝对值的两个竖杠; 矩阵的行数可以不等于列数,但是行列式的行数等于列数; 1.矩阵的数乘就是矩阵的每个…...

Flutter 开发3:创建第一个Flutter应用
Step 1: 安装Flutter 1.1 下载Flutter SDK 首先,你需要访问Flutter官方网站下载最新的Flutter SDK。选择适合你操作系统的安装包。 $ cd ~/development $ unzip ~/Downloads/flutter_macos_2.2.3-stable.zip1.2 更新环境变量 接下来,你需要将Flutter…...

Linux中断下半部分:软中断,tasklet和工作队列
为什么要有下半部分 中断会打断其他程序,为了打断其他程序时间短,就需要中断处理程序快。执行中断处理程序后,相同中断不会触发,甚至所有中断都不能触发(设置IRQF_DISABLED,其他硬件与操作系统无法通信)中…...
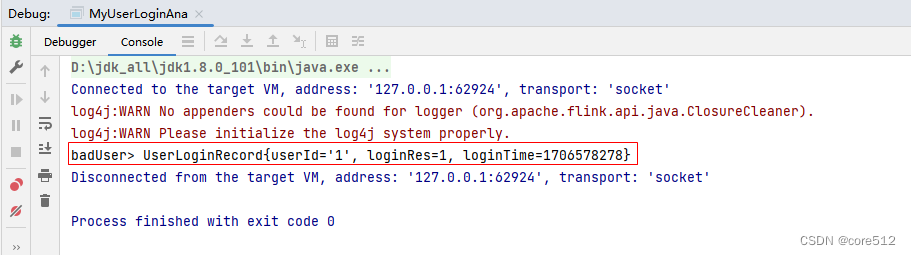
Flink CEP实现10秒内连续登录失败用户分析
1、什么是CEP? Flink CEP即 Flink Complex Event Processing,是基于DataStream流式数据提供的一套复杂事件处理编程模型。你可以把他理解为基于无界流的一套正则匹配模型,即对于无界流中的各种数据(称为事件),提供一种组合匹配的…...
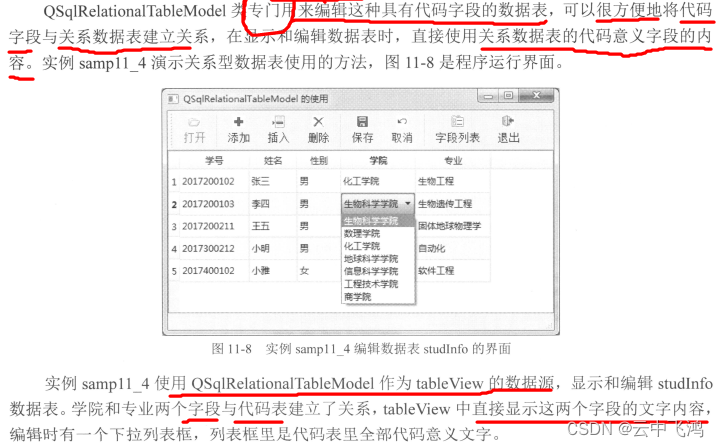
QSqlRelationalTableModel 关系表格模型
一、 1.1 QSqlRelationalTableModel继承自QSqlTableModel,并且对其进行了扩展,提供了对外键的支持。一个外键就是一个表中的一个字段 和 其他表中的主键字段之间的一对一的映射。例如,“studInfo”表中的departID字段对应的是“departments…...

JS和CSS实现的原生轮播图
JSCSS实现滑动轮播图 使用JS加CSS来实现的幻灯片,主要使用的是CSS的transform属性中的translate来实现,适合与用户交互的轮播图,展现轮播图的数量,用户可自由进行选择。 <!DOCTYPE html> <html lang"en">&…...
【微服务】skywalking自定义链路追踪与日志采集
目录 一、前言 二、自定义链路追踪简介 2.1 自定义链路追踪应用场景 2.2 链路追踪几个关键概念 三、skywalking 自定义链路追踪实现 3.1 环境准备 3.2 集成过程 3.2.1 导入核心依赖 3.2.2 几个常用注解 3.2.3 方法集成 3.2.4 上报追踪信息 四、skywalking 自定义日志…...

MYSQL基础问题
一.DBMS 是什么 DBMS(Database Management System),数据库管理系统,是一种操纵和管理 数据库的大型软件,用于建立、使用和维护数据库。对数据库进行统一的管理和 控制,以保证数据库的安全性和完整性。 二…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
