京东微前端框架MicroApp简介
一、MicroApp
1.1 MicroApp简介
MicroApp是由京东前端团队推出的一款微前端框架,它从组件化的思维,基于类WebComponent进行微前端的渲染,旨在降低上手难度、提升工作效率。MicroApp无关技术栈,也不和业务绑定,可以用于任何前端框架。
官网链接:https://micro-zoe.github.io/micro-app/
源码地址:https://github.com/micro-zoe/micro-app
微前端的概念是由ThoughtWorks在2016年提出的,它借鉴了微服务的架构理念,核心在于将一个庞大的前端应用拆分成多个独立灵活的小型应用,每个应用都可以独立开发、独立运行、独立部署,再将这些小型应用融合为一个完整的应用,或者将原本运行已久、没有关联的几个应用融合为一个应用。微前端既可以将多个项目融合为一,又可以减少项目之间的耦合,提升项目扩展性,相比一整块的前端仓库,微前端架构下的前端仓库倾向于更小更灵活。
微前端的出现主要是为了解决了两个问题:
1、随着项目迭代应用越来越庞大,难以维护。
2、跨团队或跨部门协作开发项目导致效率低下的问题。

图片
1.2 关于MicroApp
MicroApp借鉴了WebComponent的思想,通过js沙箱、样式隔离、元素隔离、路由隔离模拟实现了ShadowDom的隔离特性,并结合CustomEleme
相关文章:

京东微前端框架MicroApp简介
一、MicroApp 1.1 MicroApp简介 MicroApp是由京东前端团队推出的一款微前端框架,它从组件化的思维,基于类WebComponent进行微前端的渲染,旨在降低上手难度、提升工作效率。MicroApp无关技术栈,也不和业务绑定,可以用于任何前端框架。 官网链接:https://micro-zoe.gith…...
SpringBoot 使用定时任务(SpringTask)
Spring3.0以后自带的task,可以将它看成一个轻量级的Quartz,而且使用起来比Quartz简单许多。 使用步骤: 1.导入坐标 在spring-boot-starter-web坐标中,就包含了SpringTask,所以一般的Web项目都包含了。 <depende…...
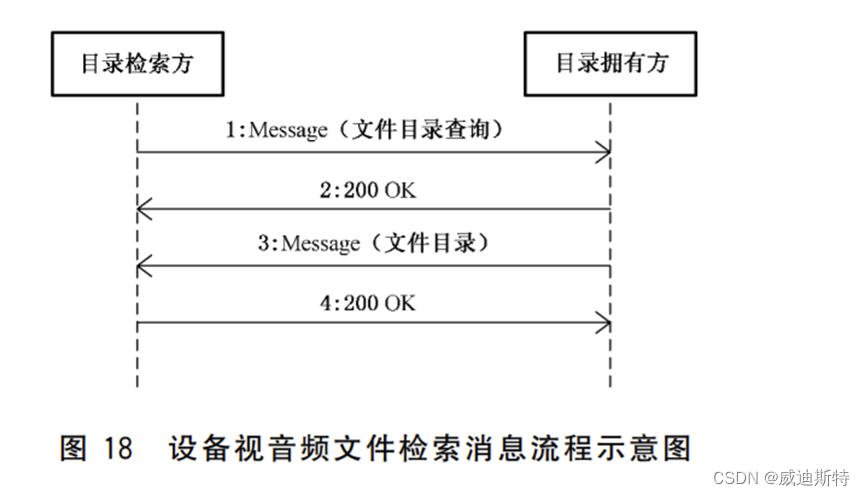
国标GB/T 28181详解:设备视音频文件检索消息流程
目 录 一、设备视音频文件检索 二、设备视音频文件检索的基本要求 三、命令流程 1、流程图 2、流程描述 四、协议接口 五、产品说明 六、设备视音频文件检索的作用 七、参考 在国标GBT28181中,定义了设备视音频文件检索消息的流程,主…...

openssl自签名CA根证书、服务端和客户端证书生成并模拟单向/双向证书验证
1. 生成根证书 1.1 生成CA证书私钥 openssl genrsa -aes256 -out ca.key 2048 1.2 取消密钥的密码保护 openssl rsa -in ca.key -out ca.key 1.3 生成根证书签发申请文件(csr文件) openssl req -new -sha256 -key ca.key -out ca.csr -subj "/CCN/STFJ/LXM/ONONE/OU…...

NIO Selector简介
1.Selector和Channel关系 Selector一般称为选择器,也叫多路复用器,NIO的核心组件,用于检查一个或多个Channel的状态是否处于可读、可写的状态。 2.可选择通道 (1)不是所有的channel都能被selector复用,…...
2023-12蓝桥杯STEMA考试 C++ 中高级试卷解析
蓝桥杯STEMA考试 C++ 中高级试卷(12月) 一、选择题 第一题 定义字符串 string a = "Hello C++",下列选项可以获取到字符 C 的是(B)。 A、a[7] B、a[6] C、a[5] D、a[4] 第二题 下列选项中数值与其它项不同的是( C)。 A、 B、 C、 D、 第三题 定义变量 int i =…...
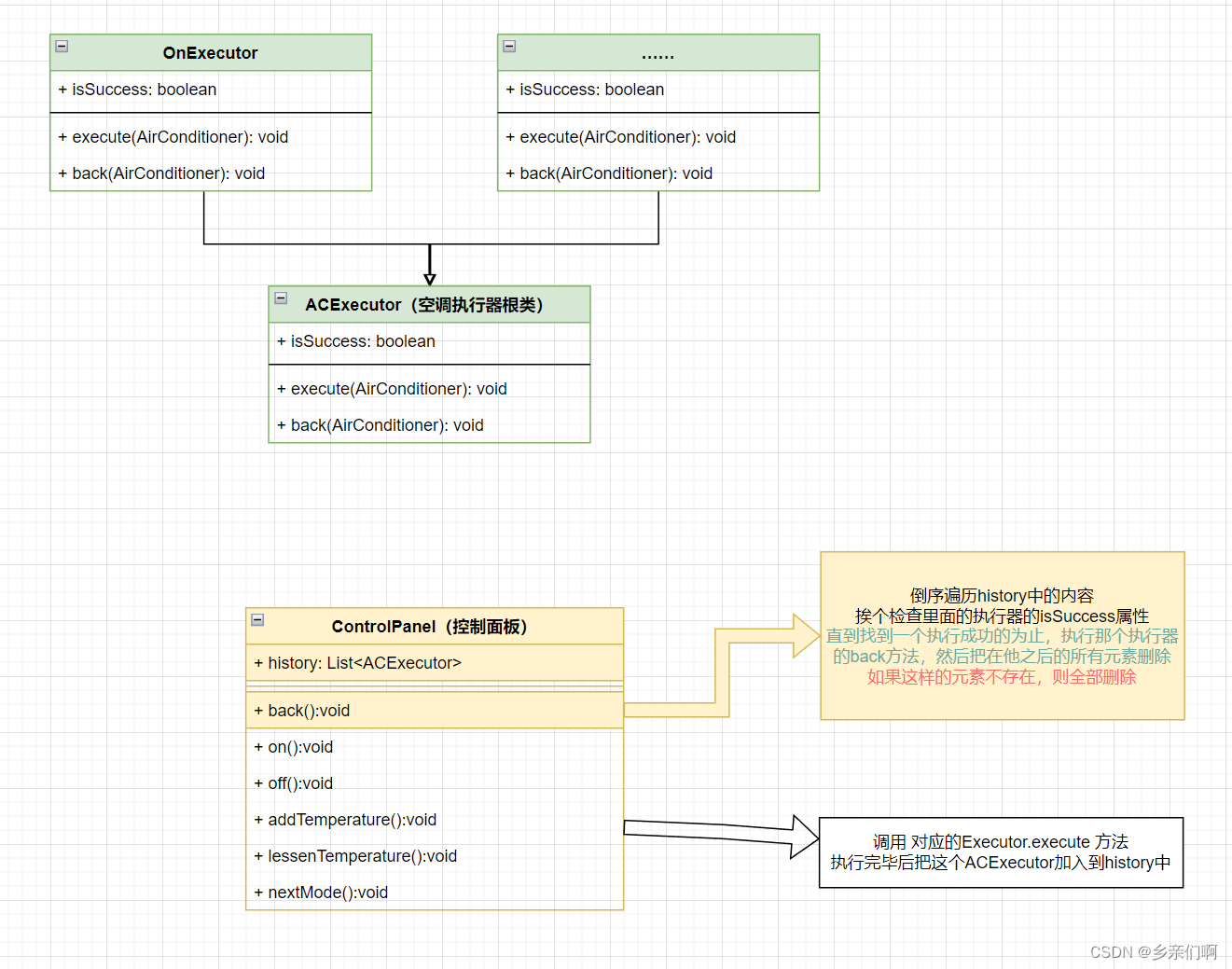
设计模式——2_1 命令(Command)
文章目录 定义图纸一个例子:空调和他的遥控器只有控制面板的空调遥控器可以撤销的操作 碎碎念命令和Runnable命令和事务 定义 把请求封装成一个对象,从而使你可以用不同的请求对客户进行参数化,对请求排队或记录请求日志,以及支持…...

HP数组面试题
PHP数组面试题 问题: 如何创建一个空数组和一个带有初始值的数组? 答案: 创建空数组:可以使用array()函数或空数组语法[]来创建一个空数组,例如$arr array();或$arr [];。创建带有初始值的数组:可以在创建…...
机器学习5-线性回归之损失函数
在线性回归中,我们通常使用最小二乘法(Ordinary Least Squares, OLS)来求解损失函数。线性回归的目标是找到一条直线,使得预测值与实际值的平方差最小化。 假设有数据集 其中 是输入特征, 是对应的输出。 线性回归的…...
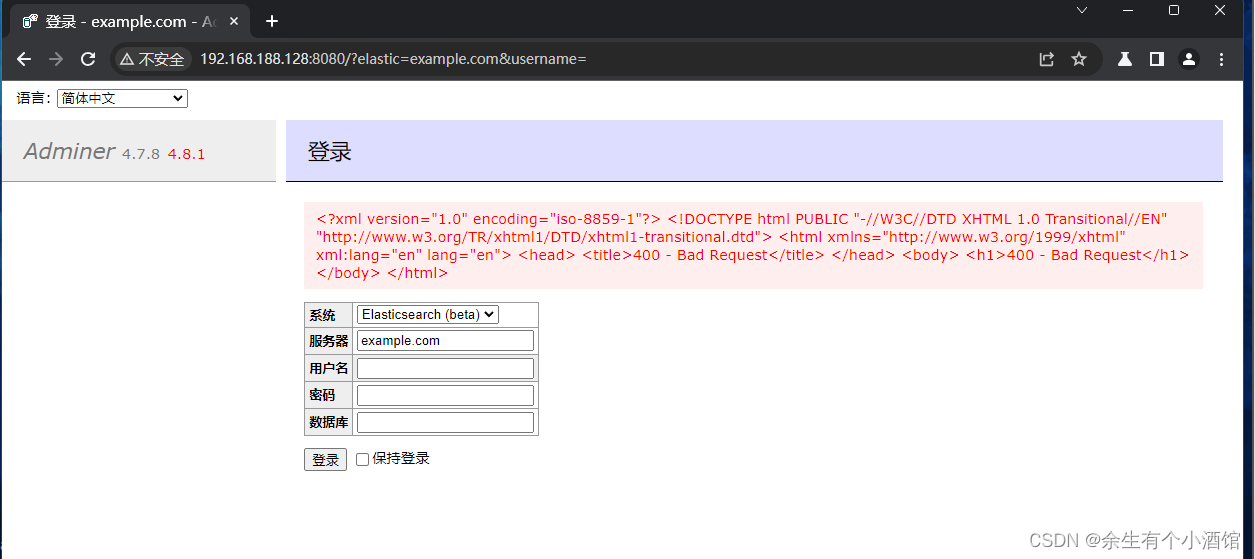
vulhub中Adminer ElasticSearch 和 ClickHouse 错误页面SSRF漏洞复现(CVE-2021-21311)
Adminer是一个PHP编写的开源数据库管理工具,支持MySQL、MariaDB、PostgreSQL、SQLite、MS SQL、Oracle、Elasticsearch、MongoDB等数据库。 在其4.0.0到4.7.9版本之间,连接 ElasticSearch 和 ClickHouse 数据库时存在一处服务端请求伪造漏洞(…...
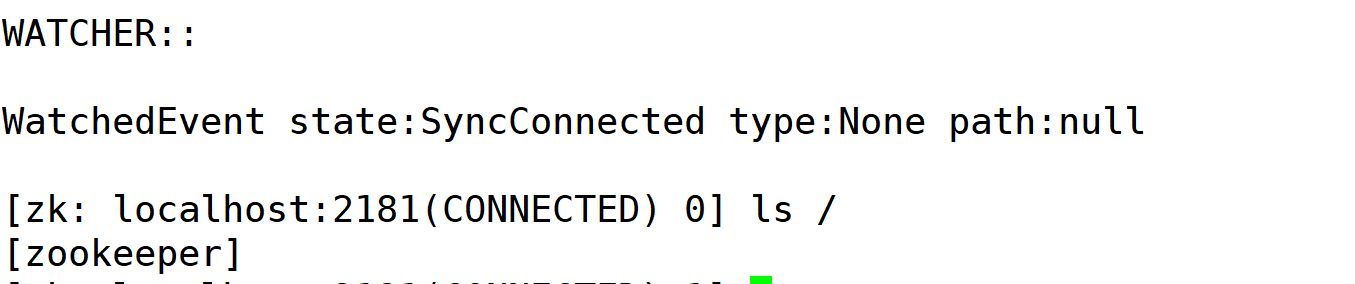
浅谈Zookeeper及windows下详细安装步骤
1. Zookeeper介绍 1.1 分布式系统面临的问题 分布式系统是一个硬件或软件组件分布在不同的网络计算机上,彼此之间仅仅通过消息传递进行通信和协调的系统。 面临的问题:系统每个节点之间信息同步及共享 以一个小团队为例,面临的问题 通过网络进行信息…...

vite, vue3, vue-router, vuex, ES6学习日记
学习使用vitevue3的所遇问题总结(2024年2月1日) 组件中使用<script>标签忘记加 setup 这会导致Navbar 没有暴露出来,导致使用不了,出现以下报错 这是因为,如果不用setup,就得使用 export default…...

25考研|660/880/1000/1800全年带刷计划
作为一个参加过两次研究生考试的老学姐,我觉得考研数学的难度完全取决于你自己 我自己就是一个很好的例子 21年数学题目是公认的简单,那一年考130的很多,但是我那一年只考了87分。但是22年又都说是有史以来最难的一年,和20年的难度…...

Mybatis基础教程及使用细节
本篇主要对Mybatis基础使用进行总结,包括Mybatis的基础操作,使用注解进行增删改查的练习;详细介绍xml映射文件配置过程并且使用xml映射文件进行动态sql语句进行条件查询;为了简化java开发提高效率,介绍一下依赖&#x…...

10 分钟在K8s 中部署轻量级日志系统 Loki
转载至我的博客 https://www.infrastack.cn ,公众号:架构成长指南 Loki 是什么? Loki是由Grafana Labs开源的一个水平可扩展、高可用性,多租户的日志聚合系统的日志聚合系统。它的设计初衷是为了解决在大规模分布式系统中&#x…...
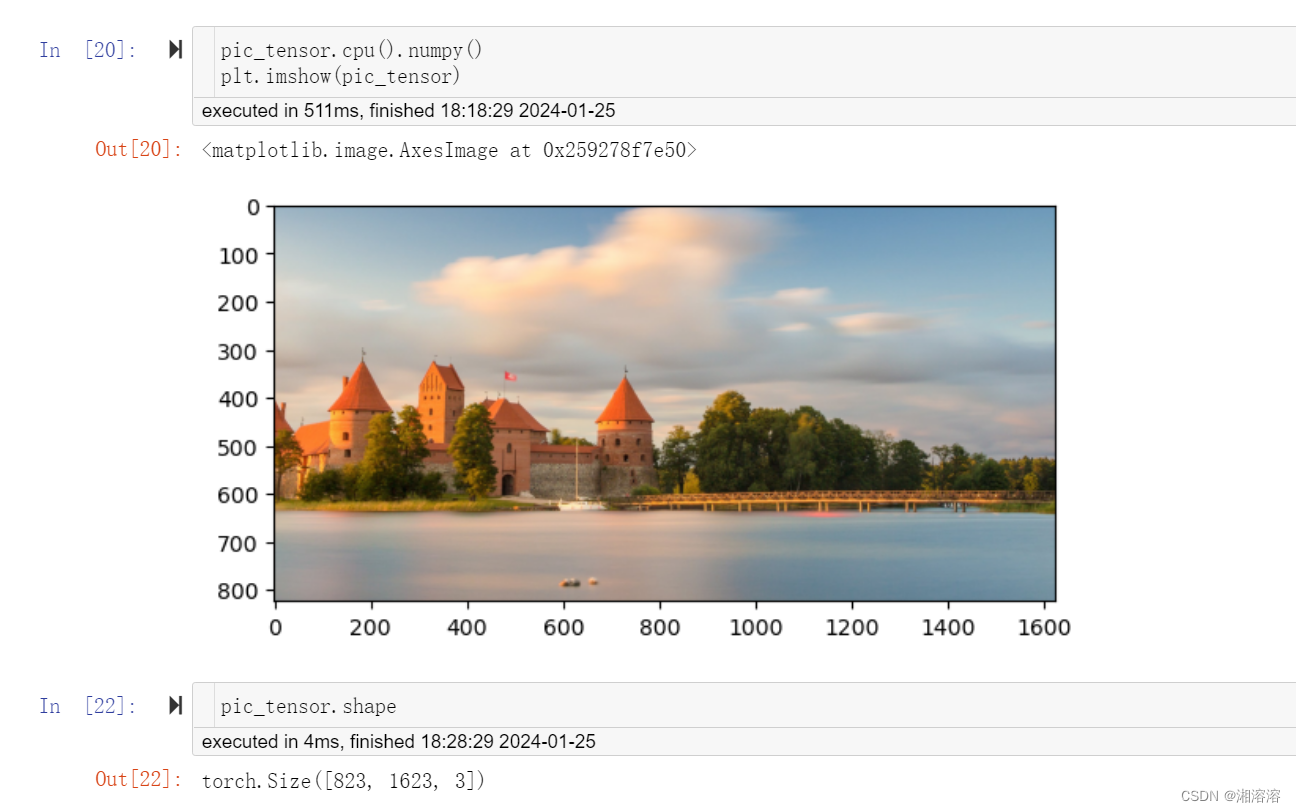
图像处理python基础
array 读取图片 tensor 模型预测 一般过程:读取数据np->tensor->model->result->np->画图 shape确保图像输入输出尺寸正确 读取图片 将在GPU上运行的tensor类型转变成在CPU上运行的np类型 三类计算机视觉任务的输入: 分类࿱…...
基于WordPress开发微信小程序2:决定开发一个wordpress主题
上一篇:基于WordPress开发微信小程序1:搭建Wordpress-CSDN博客 很快发现一个问题,如果使用别人的主题模板,多多少少存在麻烦,所以一咬牙,决定自己开发一个主题模板,并且开源在gitee上ÿ…...

[Python] 什么是网格搜索以及scikit-learn中GridSearch类的介绍和使用案例?
什么是网格搜索? 网格搜索是一种参数调优的方法,它可以帮助找到最佳的模型参数。在网格搜索中,我们先指定参数的候选值范围,然后枚举所有可能的参数组合,计算每个模型的性能指标(比如准确率、精确率等&…...
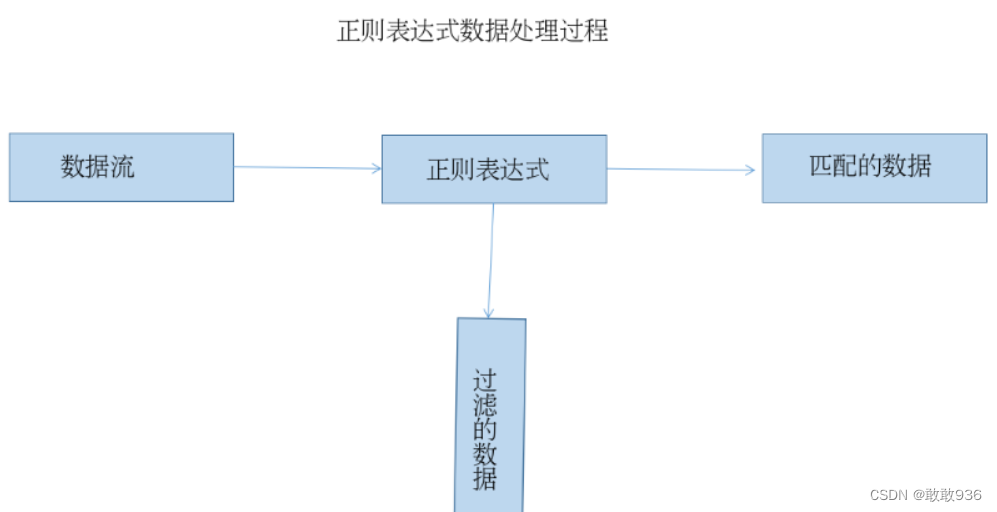
Linux-正则表达式
1.正则表达式的定义: 正则表达式通常用于判断语句中,使用字符串描述、匹配一系列符合某个规则的字符串。 正则表达式是由普通字符与元字符组成。 普通字符包括小写字母、数字、标点符号及一些其他符号。元字符是指在正则表达式中具有特殊意义的专用字符&…...

Java基础学习:System类和Static方法的实际使用
一、System类 1.在程序开发中,我们需要对这个运行的结果进行检验跟我们预判的结果是否一致,就会用到打印结果在控制台中显示出来使用到了System类。System类定义了一些和系统相关的属性和方法,它的属性和方法都是属于静态的,想使用…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
