蓝桥杯每日一题-----数位dp
前言
今天浅谈一下数位dp的板子,我最初接触到数位dp的时候,感觉数位dp老难了,一直不敢写,最近重新看了一些数位dp,发现没有想象中那么难,把板子搞会了,变通也会变的灵活的多!
引入
以一道例题作为数位dp的引入,题目如下,链接

数据范围为1e9,一般的算法很难把这道题拿下,类似求在一段区间范围内,满足某些条件的数字的个数,并且数据范围很大时就会联想到数位dp算法。
第一个板子
我遇到的数位dp板子有三个,第一个来源于y总的讲解,附上链接和这道题的代码,y总的讲解逻辑清晰,想学习可以直接看视频。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.Scanner;public class Main {static int[][] f = new int[11][10];static int k;
public static void main(String[] args) throws IOException {StreamTokenizer sc=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));sc.nextToken();//Scanner scanner = new Scanner(System.in);int t = (int)sc.nval;while(t> 0) {t--;sc.nextToken();k = (int)sc.nval;sc.nextToken();int l = (int)sc.nval;sc.nextToken();int r = (int)sc.nval;//int l = scanner.nextInt();//int r = scanner.nextInt();for (int i = 0; i < 11; i++) {Arrays.fill(f[i], 0);}init();System.out.println(dp(r) - dp(l - 1));//dp(r);}return;
}private static int dp(int num) {// TODO Auto-generated method stubif(num == 0) {return 0;}int res = 0;int last = 0;//上一个位数的数字int[] nu = new int[12];int n = 1;while (num > 0 ) {nu[n++] = num%10;num = num / 10;}n--;//System.out.println(n);for (int i = n; i > 0; i--) {//遍历位数int x = nu[i];int jj;if(i == n) {jj = 1;}else {jj = 0;}//System.out.println(x);//System.out.println(last);for (; jj < x; jj++) {//遍历该位数上可以填的数字if(Math.abs(jj - last) <= k || i == n) {//System.out.println("mm" + i);res += f[i][jj];}}if(Math.abs(x-last) <= k || i == n) {last = x;//System.out.println("1111");}else {break;}if(i==1) {res++;}}//加包含前导0的,其实就是加上不是和num同位数的数字,for (int i = 1; i < n; i++) {for (int j = 1; j < 10; j++) {//从1开始res += f[i][j];}}//System.out.println(res);return res;
}private static void init() {// TODO Auto-generated method stubfor (int i = 0; i < 10; i++) {//初始化只有一位数字的时候,一定符合要求f[1][i] = 1;//注意i一定从0开始}for (int i = 2; i < 10; i++) {//初始化其它位数的数字for (int j = 0; j < 10; j++) {//注意,这里可以包含0for (int m = 0; m < 10; m++) {if(Math.abs(m-j) <= k) {f[i][j] += f[i-1][m];}}}}
}
}
第二个板子
- 求区间[L,R]内符合条件的数字,转换为求区间[0,L-1]与[0,R]内符合条件的数字个数,答案就是这两个做差。
- 在遍历数字的时候,先遍历数字的位数,假设我要求[0,R]内满足条件的数字,R的位数为cnt,在遍历cnt的时候我要注意,不能超过R,如果R是23456,那么第cnt位能够选择的数字范围是[0,2]。如果我第cnt位选择了1,在遍历cnt-1位的时候我就不需要考虑遍历数字是否越界问题,因为cnt位已经决定了后面的位数怎么选都不会比23456大。如果第cnt位选择了2,在遍历cnt-1位时我可以填的范围就变成了[0,3],所以我需要有一个变量记录当前我前面选择的数字是否是贴上界的,令这个变量为limit,如果limit=1,当前位数可以选择的数字上界是a[cnt],否则就是9,其中数组a是把23456拆分的结果,拆分代码如下
int cnt = 0;while(n > 0) {a[++cnt] = (int) (n%10);n/=10;}
根据上述分析,会有如下代码,
int up = limit==1?a[cnt]:9;//求当前位数最大能够填的数字
limit&(i==up?1:0)//下一个limit是否还等于1,i表示当前位数填的数字,如果填了最大的那个数,且当前的limit是1,则填下一位数时能够填的最大数字也是受约束的
up表示当前位数可以填的数字上界。
-
接下来处理一下前导零,如果前导零的存在不会影响结果,那么不需要处理,否则就要处理一下前导零。比如求包含2和4的数字个数就不需要处理前导0,因为他不影响结果。如果要求数字各个位数不为0
假设我要求[0,R]内满足条件的数字,R的位数为cnt,在遍历cnt的时候我要注意,在这个位置填的0就是前导0,如果我在这个位置填了0,再去遍历第cnt-1位数字时,这里填的0还是前导0.如果我第cnt位没有填0,那么我在cnt-1位填的0就不是前导0,他是有效的一维数,就像001和101一样,00里面的0都是前导0,是无效的。而10里的0是十位上的0,是有效的。我们用zeros来表示当前位的0是否是前导0,第cnt位的0肯定是前导0,如果第cnt位填了0,第cnt-1位的0才是前导0,否则就不是。所以有zeros&(i==0?1:0)//表示下一位的zeros是否是0,i表示当前位填的数字,如果当前位填了0并且当前位的zeros是1,那么下一位的zeros也是1.
前导0的使用要比上界limit的使用更灵活一点,他是根据题目的要求来使用的。
-
这里主要讲记忆化递归。因为这一个板子用的是dfs,而dfs可能会有超时的问题,所以就有了记忆化递归。记忆化递归要标记好当前的状态,所以用来记忆当前状态的数组也是要根据题目设定。
当题目中有多个测评样例时,进行记忆化的时候要注意不要记住在特定数下的答案。所以有下面的代码if(limit == 0) dp[cnt][last][zeros] = res;
为什么要在limit=0时才进行记忆化呢?因为limit=1说明当前的数是贴上界的,而这个数是受当前这个样例影响的,比如2345这个数字,在遍历到百位数字3时,我是贴上界的,如果千位数字是2,那么此时十位数字只能选0-4,此时得到的res是从0-4递归得到的。但是如果换一个数字2377,在遍历到百位数字3时,我如果是不贴上界的,可选的数字应该是0-9,如果是贴上界的,可选的数字是0-7,明显此时的状态dp[3][3][0]和数字2345的转移是不一样的。所以我只有不贴上界的时候,说明后面的转移都是0-9时才进行记忆。
读取记忆的时候也是同样的道理,if(limit==0&&dp[cnt][last][zeros]!=-1) { return dp[cnt][last][zeros]; }
只有此时不贴上界的时候才能读取之前的记忆。
记忆化数组根据具体的题目来设定,并不是统一的,具有高度灵活性,只要解释起来没问题就可以。像小明数这道题没有记忆limit,有些情况也是可以记忆limit的。
分析题目
针对小明数而言,前导0会影响答案,为什么?题目要求相邻两数之差绝对值不超过k,如果存在前导0并且不加以判断那么会认为前导0也是有效数字,那么0后面只能填0-k,但实际前导0应该是无效数字,前面一个数字是前导0,后面可以填0~9中的任意一个数字。如果没有判断前导零,会导致结果比实际的小。 求某些数字相邻位数上的数字之差的绝对值不超过k,来想一下dfs的时候需要什么,必然要有的是当前的位数cnt和是否贴上界limit,刚刚也分析了需要判断前导零,所以有zeros。遍历到cnt位时,来判断一下当前位可以填啥,我要满足相邻位数上的数字之差的绝对值不超过k,我得知道前一个位数我填的是几,所以就有了last,指示前一个位数上填的数字。然后就没有其它的了,所以 dfs(cnt,last,zeros,limit),接下来就直接放代码了。
import java.util.Arrays;
import java.util.Scanner;
public class Main {static int dp[][][] = new int[20][20][2];//还要记录当前的状态是不是有前导零!!!!!!!static int a[] = new int[20];static int k,ans;static int nums[] = new int[20];
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();while(t-- > 0) {for(int i = 0;i < 20;i++)for(int j = 0;j < 20;j++)Arrays.fill(dp[i][j],-1);k = scanner.nextInt();long l = scanner.nextLong();long r = scanner.nextLong();System.out.println(solve(r)-solve(l-1));private static int solve(long n) {// TODO Auto-generated method stubint cnt = 0;while(n > 0) {a[++cnt] = (int) (n%10);n/=10;}return dfs(cnt,1,-1,1);
}private static int dfs(int cnt, int limit, int last,int zeros) {//前导0对答案有影响!!!!!!// TODO Auto-generated method stubif(cnt==0) {return 1;}if(limit==0&&dp[cnt][last][zeros]!=-1) {return dp[cnt][last][zeros];}int res =0;int up = limit==1?a[cnt]:9;for(int i = 0;i <= up;i++) {if(Math.abs(last-i)<=k||zeros==1) {//3 1 2 0 dp[1][0]nums[cnt] = i;res += dfs(cnt-1, limit&(i==up?1:0), i,zeros&(i==0?1:0));//120}}if(limit == 0) dp[cnt][last][zeros] = res; return res;
}
}如果代码有问题,欢迎在评论区内提出来!第三个板子就不讲啦,其实就是把第二个板子的dfs变成dp,但是个人感觉没有dfs灵活,目前在用第二个板子。
相关文章:

蓝桥杯每日一题-----数位dp
前言 今天浅谈一下数位dp的板子,我最初接触到数位dp的时候,感觉数位dp老难了,一直不敢写,最近重新看了一些数位dp,发现没有想象中那么难,把板子搞会了,变通也会变的灵活的多! 引入…...
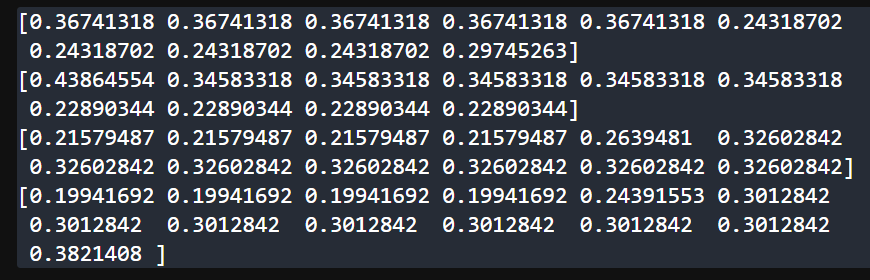
sklearn 计算 tfidf 得到每个词分数
from sklearn.feature_extraction.text import TfidfVectorizer# 语料库 可以换为其它同样形式的单词 corpus [list(range(-5, 5)),list(range(-6,4)),list(range(12)),list(range(13))]# corpus [ # [Two, wrongs, don\t, make, a, right, .], # [The, pen, is, might…...

Qt拖拽事件,实现控件内项的相互拖拽
文章目录 1拖拽演示2 步骤3 实现 这里主要以QTableview控件为例,实现表格内数据的相互拖拽。 1拖拽演示 2 步骤 自定以QTableView类,在自定义类中重写拖拽事件: void dropEvent(QDropEvent *event); void dragEnterEvent(QDragEnterEvent *…...

基于MATLAB实现的OFDM仿真调制解调,BPSK、QPSK、4QAM、16QAM、32QAM,加性高斯白噪声信道、TDL瑞利衰落信道
基于MATLAB实现的OFDM仿真调制解调,BPSK、QPSK、4QAM、16QAM、32QAM,加性高斯白噪声信道、TDL瑞利衰落信道 相关链接 OFDM中的帧(frame)、符号(symbol)、子载波(subcarriers)、导频…...
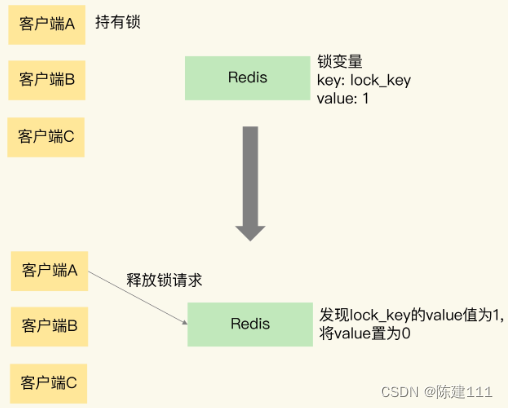
Redis核心技术与实战【学习笔记】 - 21.Redis实现分布式锁
概述 在《20.Redis原子操作》我们提到了应对并发问题时,除了原子操作,还可以通过加锁的方式,来控制并发写操作对共享数据的修改,从而保证数据的正确性。 但是,Redis 属于分布式系统,当有多个客户端需要争…...

17.Golang channel的基本定义及使用
目录 概述实践无缓冲 channel代码结果 缓冲 channel代码结果 channel的关闭特点代码结果range代码结果 select channel代码结果 结束 概述 此篇文章介绍 channel 的用法 无缓冲 channel缓冲 channelchannel的关闭特点range channelselect channel 每一种,配上完整…...

Linux - iptables 防火墙
一. 安全技术和防火墙 1.安全技术 入侵检测系统(Intrusion Detection Systems):特点是不阻断任何网络访问,量化、定位来自内外网络的威胁情况,主要以提供报警和事后监督为主,提供有针对性的指导措施和安全…...

如何在FBX剔除Lit.shader依赖
1)如何在FBX剔除Lit.shader依赖 2)Unity出AAB包(PlayAssetDelivery)模式下加载资源过慢问题 3)如何在URP中正确打出Shader变体 4)XLua打包Lua文件粒度问题 这是第371篇UWA技术知识分享的推送,精…...

cesium-测量高度垂直距离
cesium做垂直测量 完整代码 <template><div id"cesiumContainer" style"height: 100vh;"></div><div id"toolbar" style"position: fixed;top:20px;left:220px;"><el-breadcrumb><el-breadcrumb-i…...

Adobe Illustrator CEP插件开发入门指南
引言 Adobe Creative Cloud(创意云)中的Illustrator作为一款全球领先的矢量图形设计软件,为设计师提供了丰富的功能和无限的创作可能性。为了进一步增强其功能并满足个性化工作流程需求,Adobe引入了Common Extensibility Platform…...
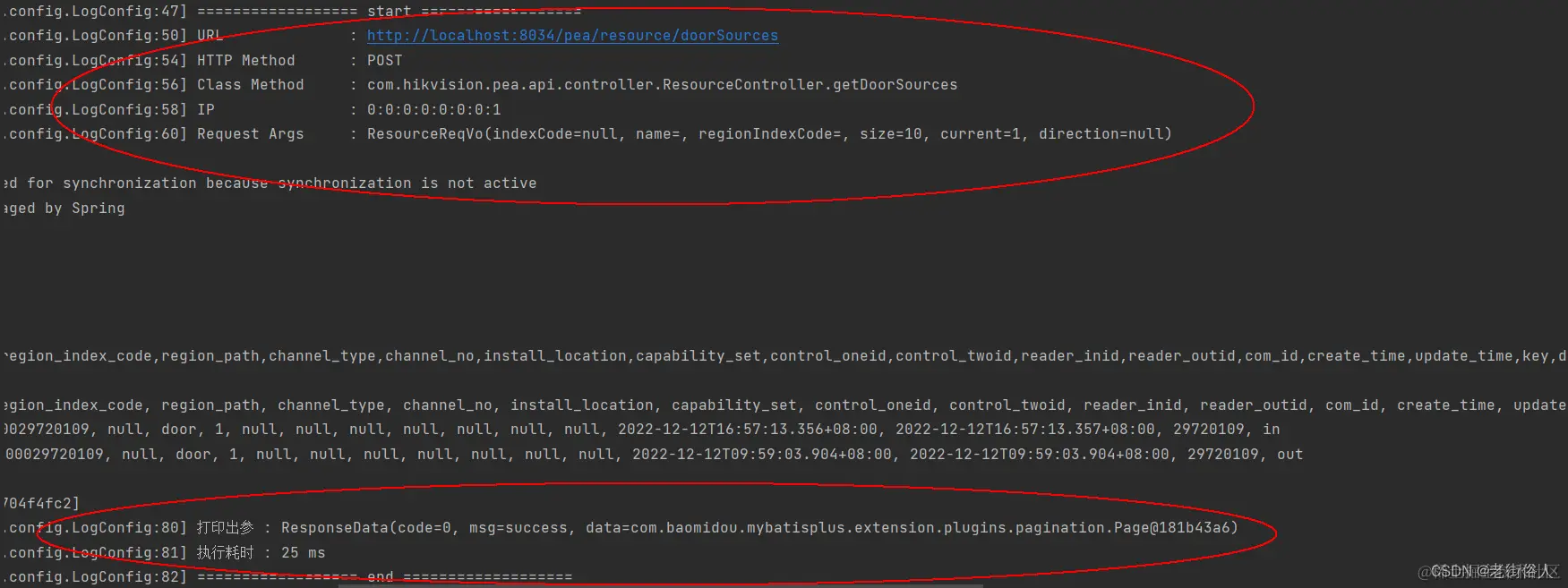
【Spring】自定义注解 + AOP 记录用户的使用日志
目录 编辑 自定义注解 AOP 记录用户的使用日志 使用背景 落地实践 一:自定义注解 二:切面配置 三:Api层使用 使用效果 自定义注解 AOP 记录用户的使用日志 使用背景 (1)在学校项目中,安防平台…...

linux互斥锁:递归锁,非递归锁用法详解
在实际的项目中经常涉及到共享资源,共享资源被多个线程访问会出现竞争现象;为了解决竞争和保护共享资源常用的机制之一就是互斥锁! 互斥锁又分为递归锁和非递归锁,互斥锁默认是非递归锁,也是我们常用的上锁方式。那么什么是递归锁和非递归锁呢? 非递归锁(Non-recursive …...

MacOS安装dmg提示已文件已损坏的解决方法
MacOS安装dmg提示已文件已损坏的解决方法 导致原因是应用没有上传到苹果的appstroe,系统限制了安装,破碎提示是苹果的误导小手段 方法 一 App 在macOS Catalina(比较新的系统,例如m1,m2也适用)下提示已损坏…...

前端输入框简单实现检测@成员输入
大体逻辑是 给input框添加一个input监听,并判断输入是否为获取当前光标的位置,你输入的肯定在光标之前,且肯定是最后一个input输入的内容换行可以被认为空格,需要进行全局替换判断成功的逻辑分为两部分,前方一般来说是…...
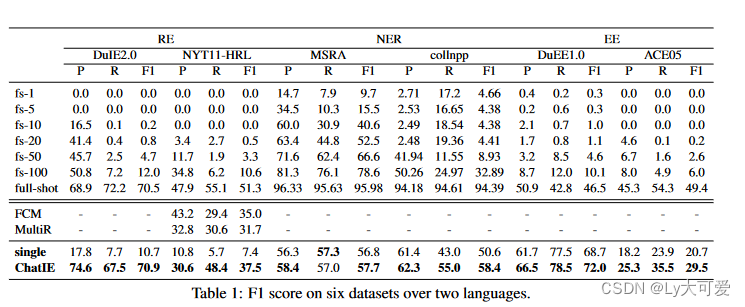
通过与chatGPT交流实现零样本事件抽取
1、写作动机: 近来的大规模语言模型(例如Chat GPT)在零样本设置下取得了很好的表现,这启发作者探索基于提示的方法来解决零样本IE任务。 2、主要贡献: 提出了基于chatgpt的多阶段的信息抽取方法:在第一阶…...

使用nodejs和html布局一个简单的视频播放网站,但是使用localhost:端口访问html无法加载视频
js代码: // app.js const express require(express); const path require(path); const app express();// 设置静态文件目录,这里假设你的视频文件在public/videos/目录下 app.use(express.static(path.join(__dirname, )));// 设置主页路由…...
【AG32VF407】国产MCU+FPGA Verilog双边沿检测输出方波
视频讲解 [AG32VF407]国产MCUFPGA Verilog双边沿检测输出方波 实验过程 本次使用使用AG32VF407开发板中的FPGA,使用双clk的双边沿进行检测,同步输出方波 同时可以根据输出的方波检测clk的频率,以及双clk的相位关系,如下为verilog…...

[晓理紫]每日论文分享(有中文摘要,源码或项目地址)--强化学习、模仿学习、机器人
专属领域论文订阅 关注{晓理紫},每日更新论文,如感兴趣,请转发给有需要的同学,谢谢支持 如果你感觉对你有所帮助,请关注我,每日准时为你推送最新论文。 为了答谢各位网友的支持,从今日起免费为3…...
为什么说TiDB在线扩容对业务几乎没有影响
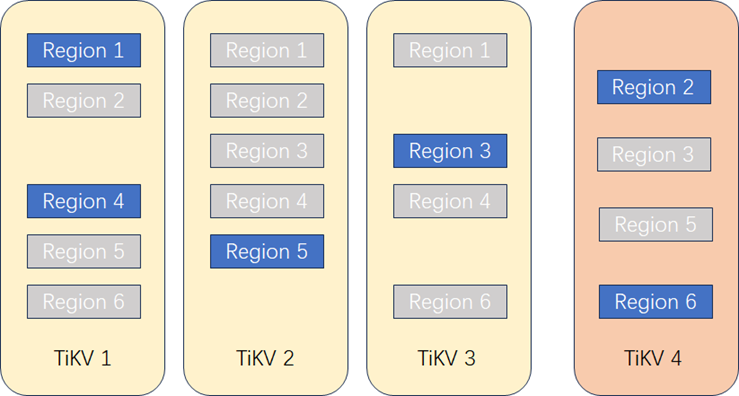
作者: 数据源的TiDB学习之路 原文来源: https://tidb.net/blog/e82b2c5f 当前的数据库种类繁多,墨天轮当前统计的所有国产数据库已经有 290个 ,其中属于关系型数据库的有 166个 。关系型数据库从部署架构上又可以分为集中式…...
STM32--SPI通信协议(2)W25Q64简介
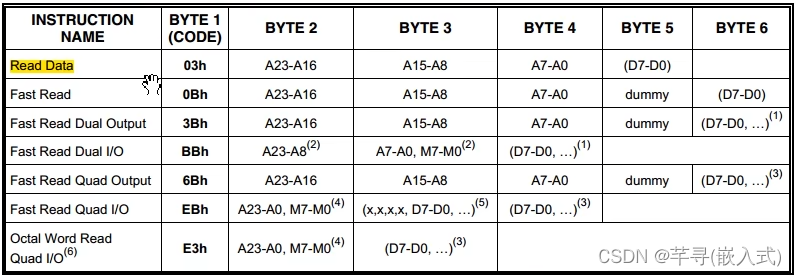
一、W25Q64简介 1、W25Qxx中的xx是不同的数字,表示了这个芯片不同的存储容量; 2、存储器分为易失性与非易失性,主要区别是存储的数据是否是掉电不丢失: 易失性存储器:SRAM、DRAM; 非易失性存储器ÿ…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
