14. 【Linux教程】文件压缩与解压
文件压缩与解压
前面小节介绍了如何对文件和目录删除、移动操作,本小节介绍如何使用命令对文件和目录进行压缩与解压操作,常见的压缩包格式有 .bz2、.Z、.gz、.zip、.xz,压缩之后的文件或目录占用更少的空间。
1. tar 命令介绍
下面列举 tar 命令的参数:
| tar 命令参数名称 | 功能与作用描述 |
|---|---|
| -c | 新建立压缩档案 |
| -x | 解压缩 |
| -t | 查看内容 |
| -u | 更新原压缩包的内容 |
| -z | gzip 属性的 |
| -j | bz2 属性的 |
| -Z | compress 属性的 |
| -v | 显示所有过程 |
| -O | 将文件解压缩成标准输出形式 |
| -f | 使用档案名字,此参数都是在最后,其后面跟上一个档案的名字 |
Tips:其中
-c、-x、-t、-u这五个参数是独立的,每次使用选其中一个,-f是最后一个参数,后面跟上档案名。
1.1 将指定类型文件打包成 tar 包
为了演示方便,先切入到 /home 目录下,使用 touch 命令创建几个 .txt 文件,然后使用 tar 命令将其打包,命令如下:
cd /hometouch a.txt b.txt c.txt d.txt e.txtls -ltar -cf alltxt.tar *.txt ls -l
执行结果如下图:
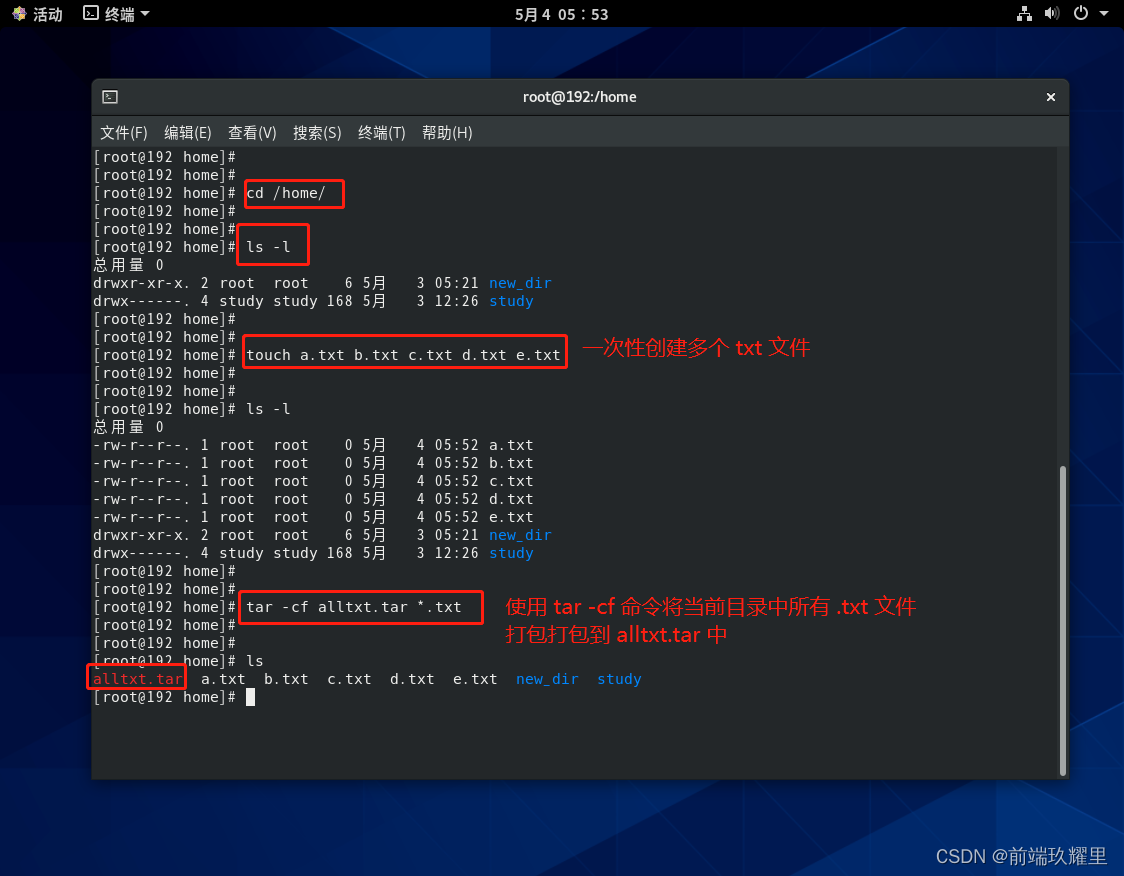
Tips:其中
alltxt.tar是一个自定义名称,后缀是tar,前半部分的名字可自行定义,*.txt中的*表示通配符代表所有的意思。
1.2 向现有的 tar 包中新增文件
这里再使用 touch 命令创建一个 g.txt 文件,使用 tar 命令将其新增至 alltxt.tar 中,命令如下:
touch g.txttar -rf alltxt.tar g.txt
执行结果如下图:
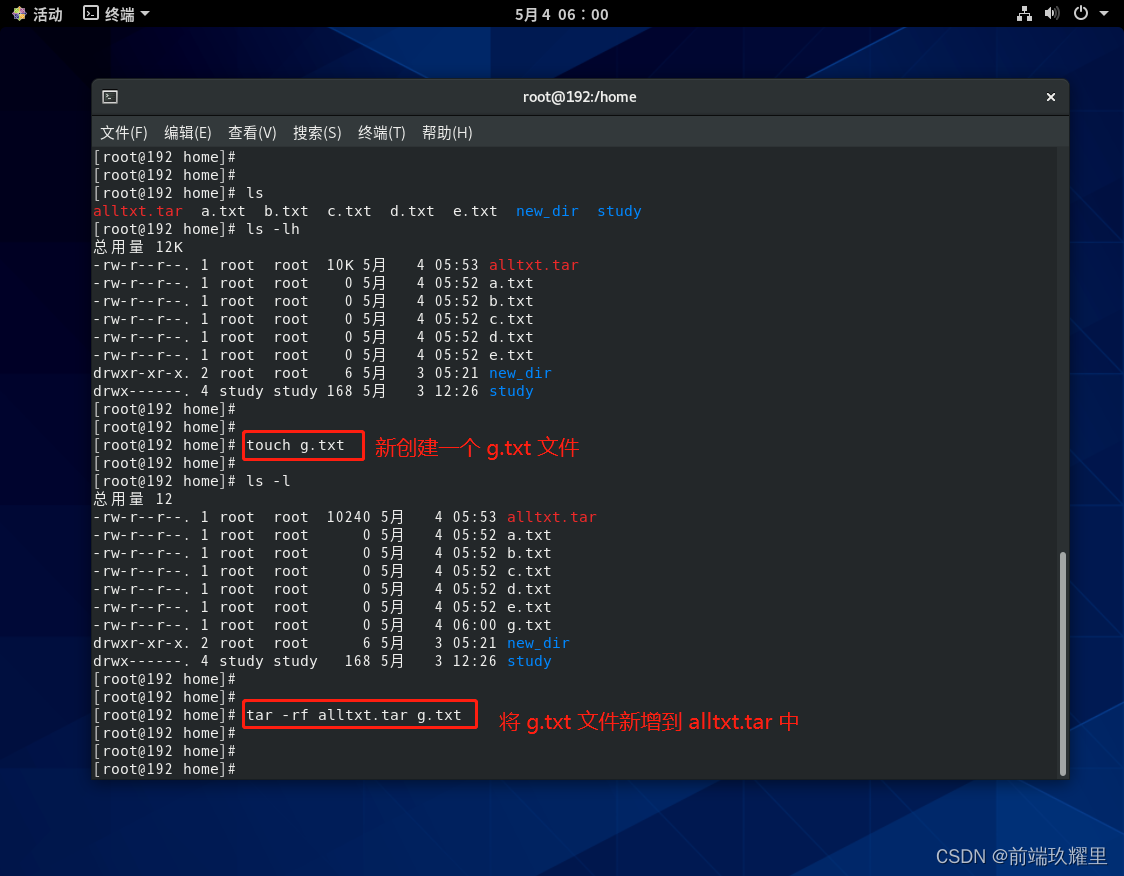
1.3 更新 原来 tar 包中的文件
使用 rm 命令删除 /home 目录中的 a.txt ,然后新建一个 a.txt 表示为更新后的 a.txt,使用 tar 命令将 a.txt 更新至 alltxt.tar 中,命令如下:
rm -f a.txttouch a.txttar -uf alltxt.tar a.txt
执行结果如下图:
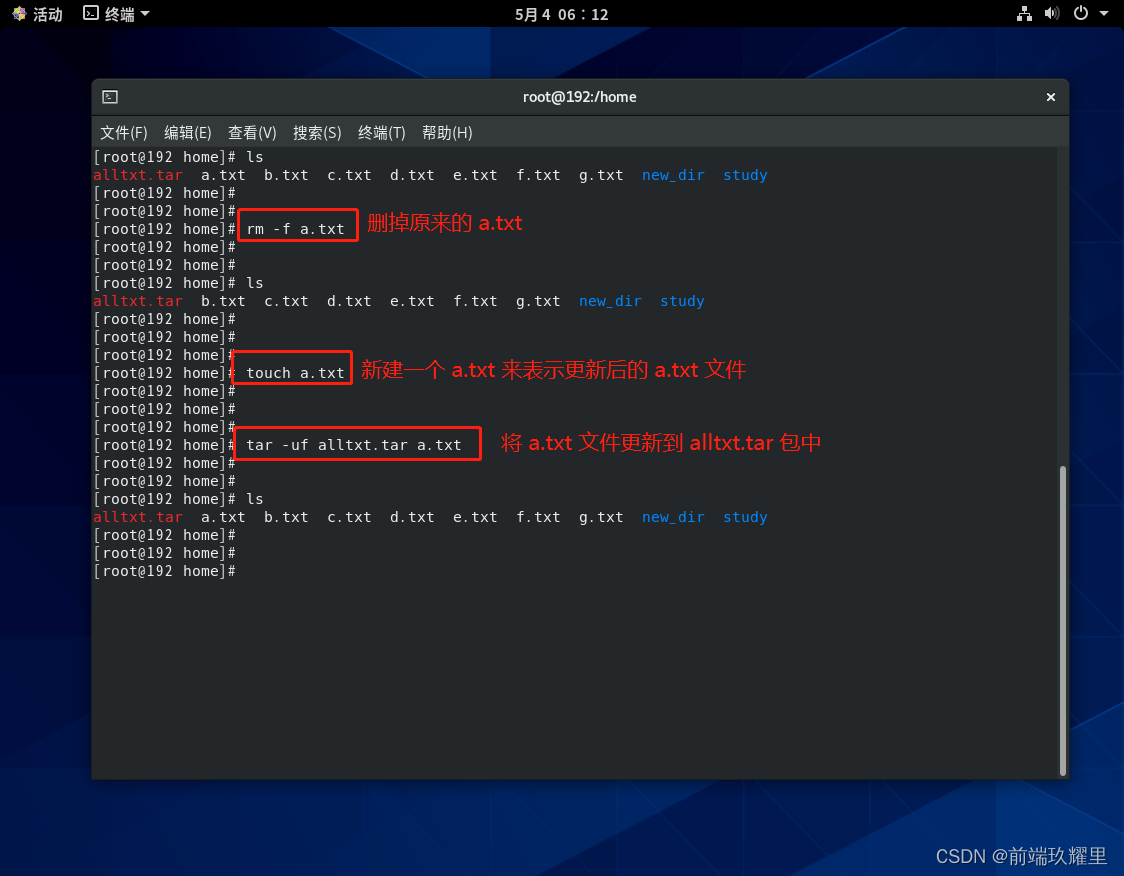
Tips:若
alltxt.tar中没有a.txt,那么使用tar -uf就会将a.txt新增到alltxt.tar中。
1.4 列出 tar 包中打包的所有文件
这里为了演示方便,将 /home 目录原有的 .txt 文件全都删除掉,然后使用 tar 命令查看 alltxt.tar 中所有文件列表,命令如下:
lsrm -f *.txtlstar -tf alltxt.tar
执行结果如下图:

1.5 解开 tar 包中所有文件
接着上面的内容,可以使用 tar 命令将 alltxt.tar 解开把文件释放到当前目录,命令如下:
lstar -xf alltxt.tarls
执行结果如下图:

1.6 使用 tar 命令压缩
上面打包的 alltxt.tar 文件并没有压缩文件,只是把文件都打包在一起,如下命令可以把 alltxt.tar 压缩成为不同格式的压缩包:
lstar -czf alltxt.tar.gz alltxt.tarlstar -cjf alltxt.tar.bz2 alltxt.tarlstar -cZf alltxt.tar.Z alltxt.tarls
执行结果如下图:
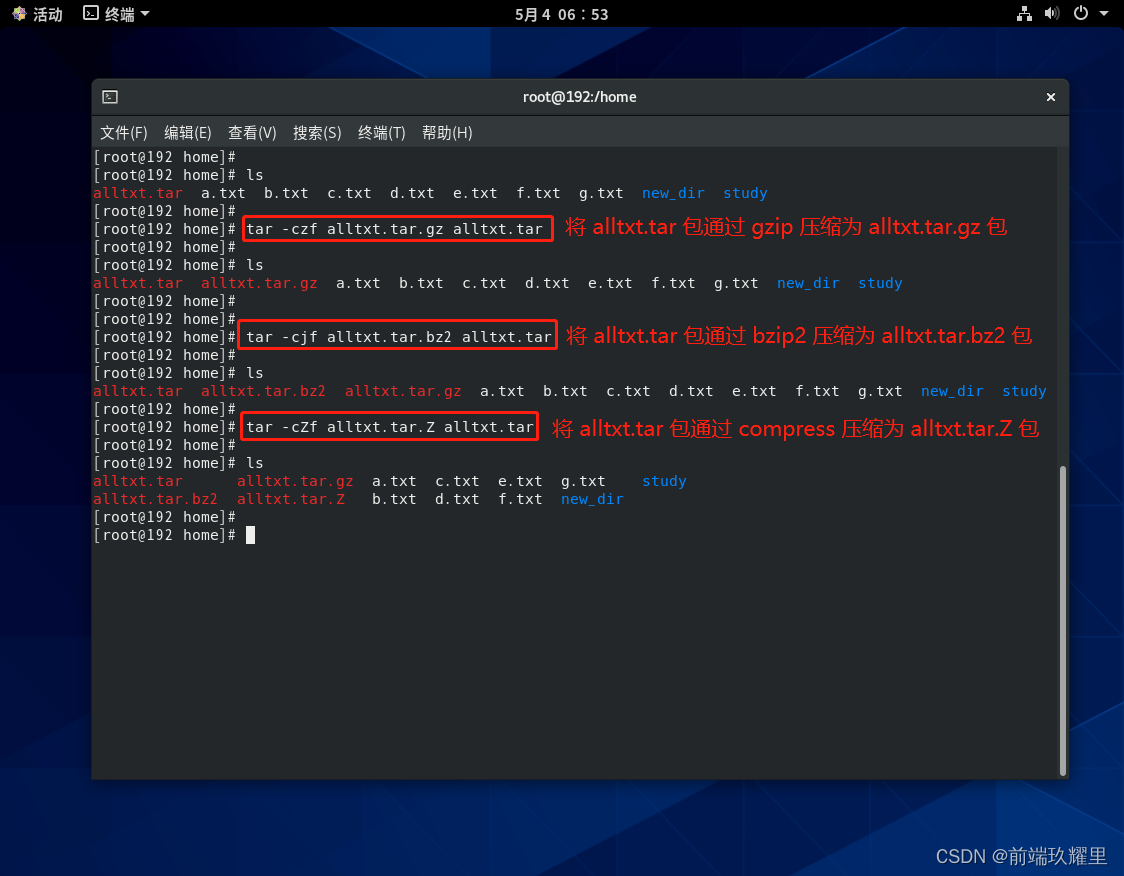
Tips:命令中参数的含义可参考前面参数表格中的功能描述。
1.7 使用 tar 命令解压缩
为了演示方便,防止读者混淆,先将 alltxt.tar.gz、alltxt.tar.bz2、alltxt.tar.Z 三种格式压缩包移动至 study 目录,然后使用 tar 命令解压,命令如下:
ls mv alltxt.tar.gz study/mv alltxt.tar.bz2 study/mv alltxt.tar.Z study/cd study/ls
移动过程执行如下图:

如上图所示,将需要解压的三种格式压缩包移动至 /home/study 目录中,下面对其解压缩,命令如下:
lstar -zxvf alltxt.tar.gzlsrm -f alltxt.tarlstar -jxvf alltxt.tar.bz2lsrm -f alltxt.tarlstar -Zxvf alltxt.tar.Zls
执行结果如下图:

Tips:命令中参数的含义可参考前面参数表格中的功能描述。
2. zip 格式压缩与解压
CentOS 8 系统中自带 zip、unzip 压缩与解压工具,可以使用 zip -v、unzip -v 命令查看当前是否安装 zip、unzip 工具,若是没有安装,则可以使用如下命令安装:
yum -y updateyum -y install zip unzip安装过程如下图:
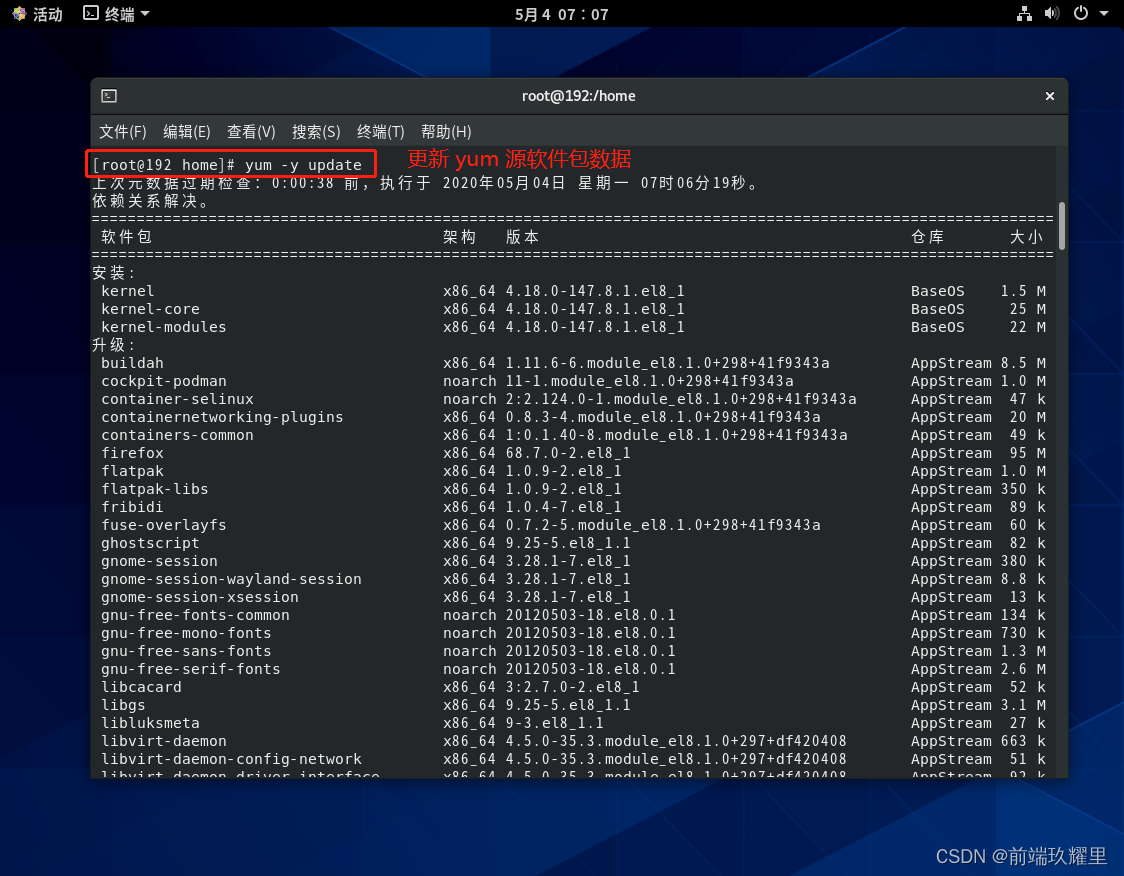
如上图所示,先要更新 yum 源的软件包数据,如下图所示为安装 zip、unzip 的过程执行图:
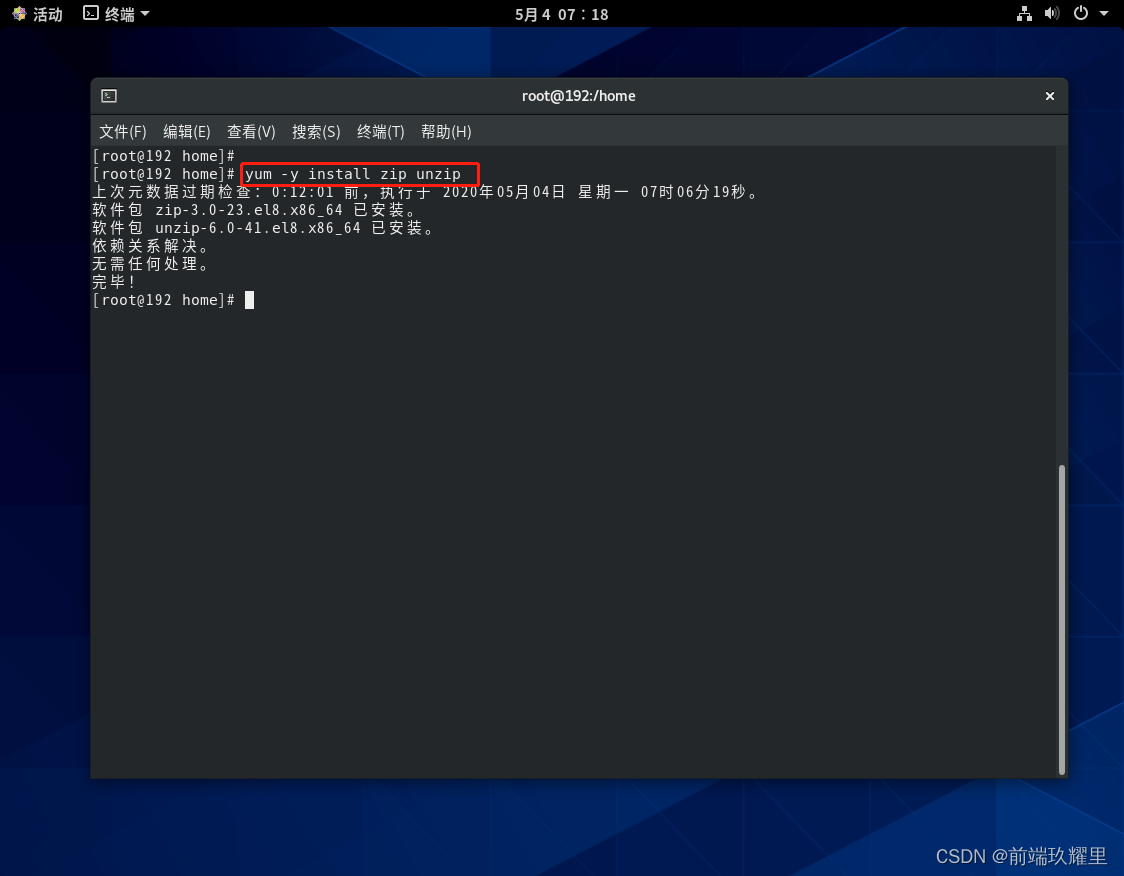
Tips:
yum是 Linux 中的一个软件管理仓库,关于yum如何安装软件后续小节会详细介绍。
2.1 使用 zip 压缩文件
使用 zip 命令可以将 alltxt.tar 包压缩为 .zip 压缩包,命令如下:
lszip alltxt.zip alltxt.tarls
执行结果如下:

Tips:可以使用
zip -r zip包名 目录名递归压缩目录以及目录中所有文件。
2.2 使用 unzip 解压缩
为了演示方便,先将 alltxt.zip 文件移动至 /home/study 中,然后解压,命令如下:
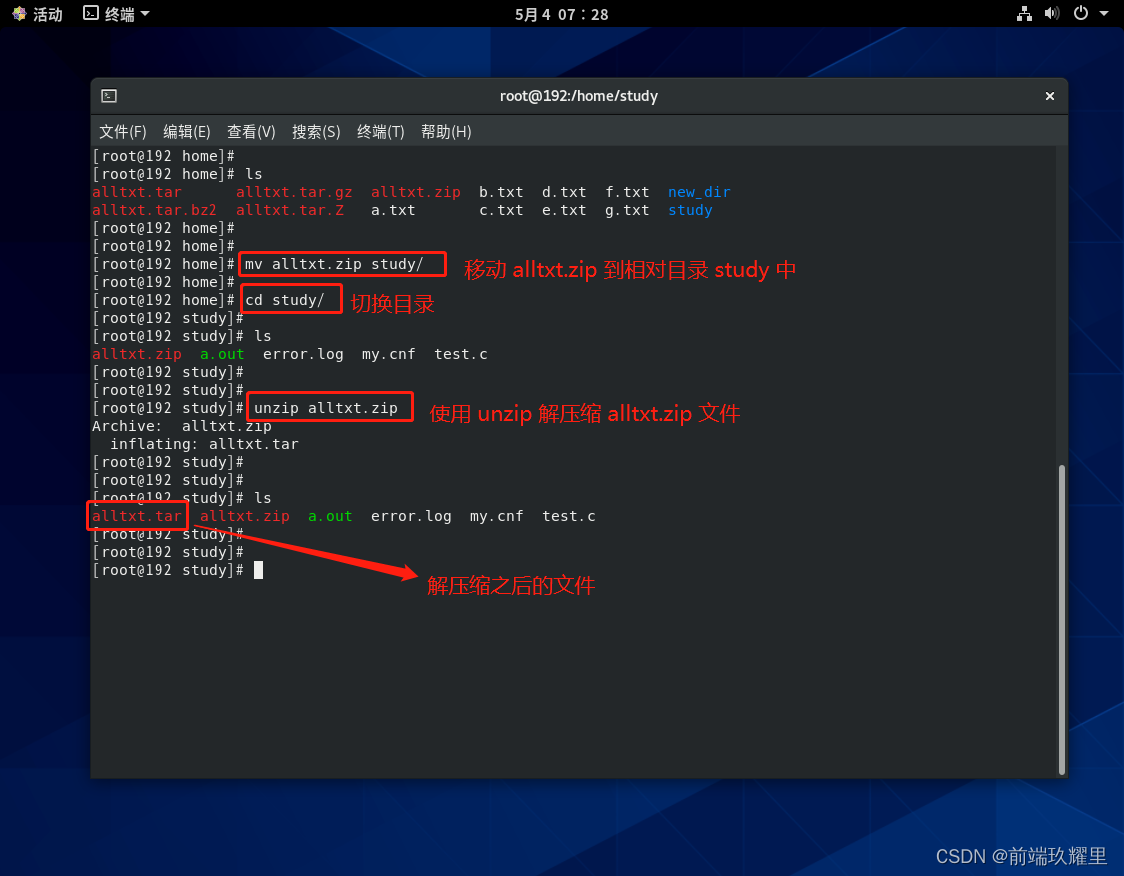
lsmv alltxt.zip study/cd study/lsunzip alltxt.zipls
执行结果如下图:
3. 小结
本小节介绍了如何使用 tar 命令打包文件和解开 tar 包,还介绍了如何使用 tar 将文件包压缩为 .gz、.bz2、.Z 格式的压缩包,如何解压缩它们,最后还介绍了如何使用 zip、unzip 工具压缩与解压 .zip 格式的压缩包,需要注意的是使用 tar 命令将文件打包成 tar 包之后,文件并没有被压缩,只是打包在一起了,压缩文件前,也可以不打包成 tar 包,可以直接对某个文件和目录进行压缩。
相关文章:

14. 【Linux教程】文件压缩与解压
文件压缩与解压 前面小节介绍了如何对文件和目录删除、移动操作,本小节介绍如何使用命令对文件和目录进行压缩与解压操作,常见的压缩包格式有 .bz2、.Z、.gz、.zip、.xz,压缩之后的文件或目录占用更少的空间。 1. tar 命令介绍 下面列举 ta…...
ruoyi-nbcio中xxl-job的安装与使用
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址: http://122.227.135.243:9666 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbach…...

从零学算法162
162.峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。 你可以假设 nums[-1] nums[n] -∞ 。 你必须实现时间复杂度为 O…...
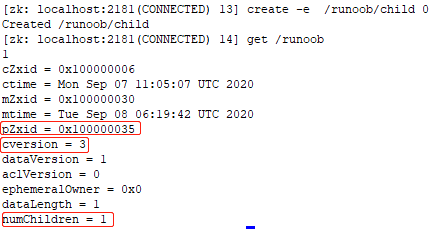
5.0 ZooKeeper 数据模型 znode 结构详解
数据模型 在 zookeeper 中,可以说 zookeeper 中的所有存储的数据是由 znode 组成的,节点也称为 znode,并以 key/value 形式存储数据。 整体结构类似于 linux 文件系统的模式以树形结构存储。其中根路径以 / 开头。 进入 zookeeper 安装的 …...

《数电》理论笔记-第1章-逻辑代数基础
参考:视频 和 《数字电路与逻辑设计》 电子书 一,第1章 逻辑代数基础 1 数字量和模拟量 略 2 数制(十进制,二进制,八进制和十六进制) 拨电话(BoDH)---(2八10十六&…...

计算指定路径下的可用空间大小
方法一、使用psutil库 import psutildef check_disk_space(path):usage psutil.disk_usage(path)## 1GB 1 * 1024 * 1024 * 1024字节if usage.free > 1 * 1024 * 1024 * 1024:return 1else:return 0disk_path "/home" result check_disk_space(disk_path) pr…...

2023年全球软件架构师峰会(ArchSummit上海站):核心内容与学习收获(附大会核心PPT下载)
微服务架构是当今软件架构的主流趋势之一。随着云计算和分布式系统的普及,越来越多的企业开始采用微服务架构来构建他们的应用。微服务架构可以将一个大型的应用拆分成多个小型的服务,每个服务都独立部署、独立运行,并通过轻量级的通信协议进…...
)
踩坑实录(Second Day)
作为公司的小菜鸟,每天都踩坑应该是一件很正常的事情吧,哈哈哈。今天遇到了比较棘手的问题,以前从来没有遇到过。然后就是在某平台上接的一个 bug 修改的单子,也拿出来和大家分享一下~ 此为第二篇(2024 年 02 月 05 日…...

已解决org.springframework.web.HttpMediaTypeNotAcceptableException异常的正确解决方法,亲测有效!!!
已解决org.springframework.web.HttpMediaTypeNotAcceptableException异常的正确解决方法,亲测有效!!! 文章目录 问题分析 报错原因 解决思路 解决方法 总结 问题分析 在Spring MVC应用中处理HTTP请求时,我们有…...
根据MySql建表语句创建Java实体类工具
点击下载《根据MySql建表语句创建Java实体类工具》 1. 前言 在软件开发领域,特别是在构建企业级应用时,数据模型与代码模型之间的映射是至关重要的。该软件是一款基于C#开发的高效工具,它将这一繁琐且容易出错的过程变得简洁且快速。此工具…...
做跨境电商需要使用住宅代理IP吗?
住宅代理IP是近年来跨境电商领域日益受到重视的技术工具,不仅可以保护隐私、优化网络速度,还能助推跨境电商的精细化管理。接下来,我们将深入探讨利用住宅代理IP如何为跨境电商业务带来竞争优势。 一、住宅代理IP与跨境电商 住宅代理IP&…...

vue3 之 组合式API—reactive和ref函数
ref() 作用:接收简单类型或者对象类型的数据传入并返回一个响应式的对象 核心步骤: 1️⃣ 从 vue 包中导入 ref 函数 2️⃣在 <script setup>// 导入import { ref } from vue// 执行函数 传入参数 变量接收const count …...

Python库-PyAutoGUI
pyautogui是一个Python库,可以自动控制键盘和鼠标,非常适合进行自动化任务。它可以用于各种场景,比如自动化测试、数据录入任务,甚至是简单的游戏机器人。下面是一个关于pyautogui的入门教程,包括它的安装、基本使用方…...

越权测试是什么?
一、越权测试是什么? 越权漏洞是web应用程序中常见的一种安全漏洞。它的威胁在于一个账户可控制全站用户数据。越权漏洞产生的原因主要是因为开发人员在对数据进行增删改查时对客户端的请求数据过分相信而遗漏了权限的判定。 二、越权漏洞的分类 越权分为2种&…...
H5 简约四色新科技风引导页源码
H5 简约四色新科技风引导页源码 源码介绍:一款四色切换自适应现代科技风动态背景的引导页源码,源码有主站按钮,分站按钮2个,QQ联系站长按钮一个。 下载地址: https://www.changyouzuhao.cn/11990.html...

使用 VTK 中的单元定位器来查找最近的点
开发环境: Windows 11 家庭中文版Microsoft Visual Studio Community 2019VTK-9.3.0.rc0vtk-example demo解决问题:使用 VTK 中的单元定位器来查找最近的点 关键点: 创建了一个球体数据源,并使用它构建了一个单元定位器&#x…...
时序预测 | MATLAB实现基于CNN-LSTM-AdaBoost卷积长短期记忆网络结合AdaBoost时间序列预测
时序预测 | MATLAB实现基于CNN-LSTM-AdaBoost卷积长短期记忆网络结合AdaBoost时间序列预测 目录 时序预测 | MATLAB实现基于CNN-LSTM-AdaBoost卷积长短期记忆网络结合AdaBoost时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现基于CNN-LST…...

Xcode 15 及以上版本:libarclite 库缺少问题
参考链接:Xcode 15 libarclite 缺失问题_sdk does not contain libarclite at the path /ap-CSDN博客 报错: SDK does not contain libarclite at the path /Applications/Xcode.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/lib/arc/libarcl…...

Spring设计模式之单例模式
文章目录 一、概述二、单例模式的优点三、Spring中的单例模式四、单例模式的实现方式五、总结 一、概述 单例模式是一种创建型设计模式,确保一个类只有一个实例,并提供一个全局访问点来获取该实例。在Spring框架中,单例模式是默认的Bean定义…...
Fink CDC数据同步(二)MySQL数据同步
1 开启binlog日志 2 数据准备 use bigdata; drop table if exists user;CREATE TABLE user(id INTEGER NOT NULL AUTO_INCREMENT,name VARCHAR(20) NOT NULL DEFAULT ,birth VARCHAR(20) NOT NULL DEFAULT ,gender VARCHAR(10) NOT NULL DEFAULT ,PRIMARY KEY(id) ); ALTER TA…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
