【射影几何15】python双曲几何工具geometry_tools
目录
- 一、说明
- 二、环境问题:如何安装
- 三、实现一个简单的例子
- 四、绘制双曲组
- 五、使用有限状态自动机加快速度
- 六、资源和代码
一、说明
Geometry_tools 是一个 Python 包,旨在帮助您处理和可视化双曲空间和射影空间上的群动作。
该包主要构建在 numpy、matplotlib 和 scipy 之上。或者,该包可以使用 Sage 提供的工具来执行(缓慢的)精确计算。
几何工具可以帮助您:
-
在多个模型(即克莱因模型、双曲面模型、射影模型、庞加莱模型和半空间模型)中对双曲空间中的对象执行数值(或有时是精确)计算
-
在双曲平面、实射影平面、复射影线上画出漂亮的图画
-
将有限生成组的表示处理为 O ( d , 1 ) \textrm{O}(d, 1) O(d,1)
, GL ( d , R ) \textrm{GL}(d, \mathbb{R}) GL(d,R), 和 GL ( d , C ) \textrm{GL}(d, \mathbb{C}) GL(d,C) -
使用 Coxeter 群的表示进行实际计算 GL ( d , R ) \textrm{GL}(d, \mathbb{R}) GL(d,R)
-
使用有限状态自动机在字双曲群中进行一些简单的计算在双曲平面、实射影平面、复射影线上画出漂亮的图画
还提供了对 3D 图形的一些有限支持(通过 matplotlib)。
这个包的所有功能(在数学上)都不是很深。大多数情况下,该软件包只是包装了更复杂的工具,旨在使您可以轻松地快速绘制好图画。在, H 2 \mathbb{H}^2 H2,和 H 3 \mathbb{H}^3 H3 和 R P 2 \mathbb{R}P^2 RP2 和 C P 1 \mathbb{C}P^1 CP1。
二、环境问题:如何安装
现在,最简单的安装方法是从 git 存储库下载或克隆geometry_tools项目,然后运行
pip install .
从您下载它的目录中。如果您没有安装 pip,则应先安装 pip。或者,您可以尝试从项目目录运行(不建议这样做)。
python setup.py install
三、实现一个简单的例子
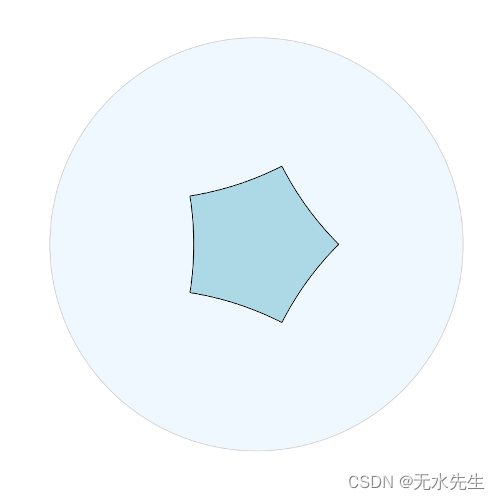
要在双曲平面上绘制直角五边形的图片:
from geometry_tools import hyperbolic, drawtools
from numpy import pi# make a right-angled pentagon
pentagon = hyperbolic.Polygon.regular_polygon(5, angle=pi/2)# draw the pentagon
figure = drawtools.HyperbolicDrawing()
figure.draw_plane()
figure.draw_polygon(pentagon, facecolor="lightblue")figure.show()
代码结果:
四、绘制双曲组
该软件包方便绘制平铺图片geometry_tools在 H 2 \mathbb{H}^2 H2空间.在这里,我们将可视化 (2,3,7) 三角形平铺:
from geometry_tools import hyperbolic, coxeter, drawtools
from geometry_tools.automata import fsa# make the triangle group representation and load a finite-state automaton
triangle_group = coxeter.TriangleGroup((2,3,7))
triangle_rep = triangle_group.hyperbolic_rep()
triangle_fsa = triangle_group.automaton()# find a fundamental domain for the action by finding
# fixed points of length-2 elements
vertices = triangle_rep.isometries(["ab", "bc", "ca"]).fixed_point()
fund_triangle = hyperbolic.Polygon(vertices)# find all orientation-preserving isometries of length at most 30
words = triangle_fsa.enumerate_words(30)
even_words = [word for word in words if len(word) % 2 == 0]
pos_isometries = triangle_rep.isometries(even_words)# draw the translated triangles
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(pos_isometries @ fund_triangle, facecolor="royalblue", edgecolor="none")fig.show()
首先,首先实例化该类coxeter.TriangleGroup以获得一个 (2,3,7) 三角形组,并将其几何表示计算为双曲平面的等距:
# get a representation for a triangle group.
# (these are built in to the program)
from geometry_tools import hyperbolic, coxeter, drawtoolstriangle_rep = coxeter.TriangleGroup((2,3,7)).hyperbolic_rep()
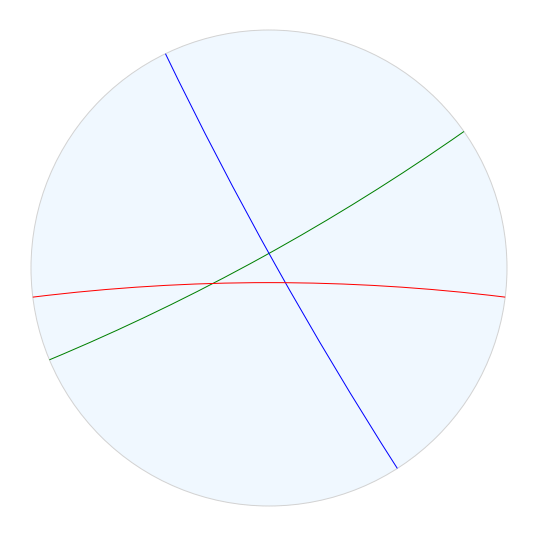
我们可以使用子包绘制组的反射墙:geometry_tools.drawtools
# find the fixed points at infinity for the generating reflectionsreflections = triangle_rep.isometries(["a", "b", "c"])
walls = hyperbolic.Geodesic.from_reflection(reflections)wall_a, wall_b, wall_c = wallsfig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()fig.draw_geodesic(wall_a, color="green")
fig.draw_geodesic(wall_b, color="blue")
fig.draw_geodesic(wall_c, color="red")
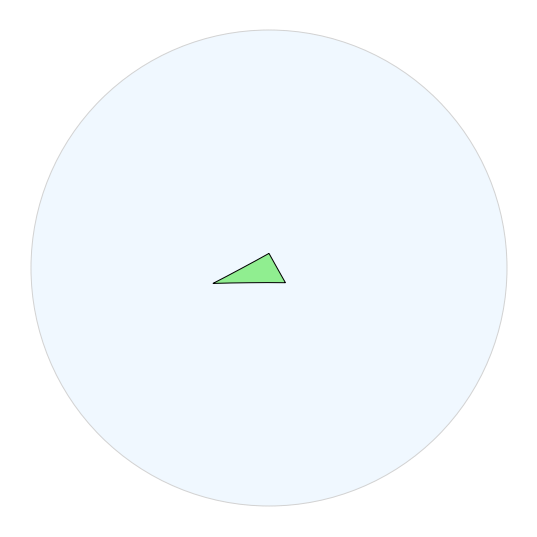
我们可以通过取三角形群的顶点是群的长度 2 元素的固定点的三角形来找到三角形群的基本域。
triangle_vertices = triangle_rep.isometries(["ab", "bc", "ac"]).fixed_point()
fund_triangle = hyperbolic.Polygon(triangle_vertices)
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(fund_triangle, facecolor="lightgreen")
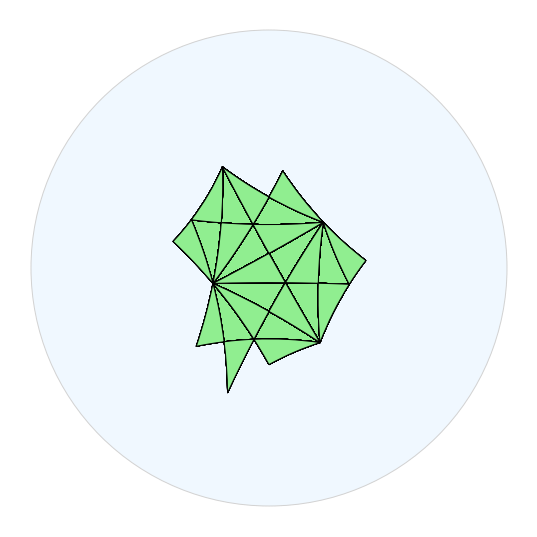
如果我们想开始可视化 ( H 2 ) (\mathbb{H}^2) (H2)我们从这个三角形组中得到,我们可以开始绘制这个基本域的翻译。要做到这一点,最简单(但效率较低且吸引人)的方法是,只绘制由组中自由简化的单词图像翻译的基本域的副本。
words = triangle_rep.free_words_less_than(5)
isometries = triangle_rep.isometries(words)tiles = isometries @ fund_trianglefig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()fig.draw_polygon(tiles, facecolor="lightgreen")
五、使用有限状态自动机加快速度
绘制由所有自由缩小的单词的图像翻译的三角形的副本有点慢。而且,我们最终多次在其顶部绘制同一个三角形。我们可以使用有限状态自动机为组中的每个元素选择一个唯一的单词,从而加快该过程。
Geometry_tools.automata 子包提供了一些用于处理有限状态自动机的工具。它可以加载和操作 kbmag 程序生成的自动机。虽然 kbmag 不包含在 Geometry_tools 中,但该包确实为许多单词双曲群提供了预先计算的自动机。要获取预先计算的自动机列表,请导入 automata.fsa 子模块并调用 fsa.list_builtins()。调用 fsa.load_builtin() 加载自动机。
感谢 Florian Stecker 提供的代码,geometry_tools 包还可以为任何 Coxeter 组生成自动机。所以我们可以得到 (2,3,7) 三角形组的自动机,如下所示:
# construct the (2,3,7) automaton
triangle_fsa = coxeter.TriangleGroup((2,3,7)).automaton()# get a unique word for each group element of length < 25.
# (we convert to a list since enumerate_words returns a generator)
words = list(triangle_fsa.enumerate_words(30))free_words = list(triangle_rep.free_words_less_than(9))# compare unique words of length <30 to freely reduced words of length <9.
# when we don't consider the relation, we get many redundant words!
len(words), len(free_words)
(5951, 585937)
为了让图片更漂亮一点,我们可以制作一个只接受偶数长度的单词的自动机。然后我们可以得到所有等距的集合,这些等距是这个自动机接受的单词的图像。
even_triangle_fsa = triangle_fsa.even_automaton()
pos_isometries = triangle_rep.automaton_accepted(even_triangle_fsa, 15)tiles = pos_isometries @ fund_trianglefig = drawtools.HyperbolicDrawing()
fig.draw_plane()
fig.draw_polygon(tiles, facecolor="royalblue", edgecolor="none")

回顾一下,以下是生成上图所需的所有代码:
from geometry_tools import hyperbolic, coxeter, drawtools# make the triangle group representation
triangle_group = coxeter.TriangleGroup((2,3,7))
triangle_rep = triangle_group.hyperbolic_rep()# find a fundamental domain for the action by finding
# fixed points of length-2 elements
vertices = triangle_rep.isometries(["ab", "bc", "ca"]).fixed_point()
fund_triangle = hyperbolic.Polygon(vertices)# find all orientation-preserving isometries of length at most 30 using an automaton
triangle_fsa = triangle_group.automaton(even_length=True)
pos_isometries = triangle_rep.automaton_accepted(triangle_fsa, 15)# draw the translated triangles
fig = drawtools.HyperbolicDrawing(model="poincare")
fig.draw_plane()
fig.draw_polygon(pos_isometries @ fund_triangle, facecolor="royalblue", edgecolor="none")
六、资源和代码
本文资源下载地址是:
https://download.csdn.net/download/gongdiwudu/88826390
(未完待续)
相关文章:

【射影几何15】python双曲几何工具geometry_tools
目录 一、说明二、环境问题:如何安装三、实现一个简单的例子四、绘制双曲组五、使用有限状态自动机加快速度六、资源和代码 一、说明 Geometry_tools 是一个 Python 包,旨在帮助您处理和可视化双曲空间和射影空间上的群动作。 该包主要构建在 numpy、…...

机器人抓取 [ 题目/摘要 ] 更新中..
题目:Robotic Grasping of Novel Objects using Visionl 链接:机器人抓取新物体 | IEEE Xplore(IEEE的Xplore) 【端到端】 摘要:我们考虑抓取新物体的问题,特别是第一次通过视觉看到的物体。抓取以前未知的…...
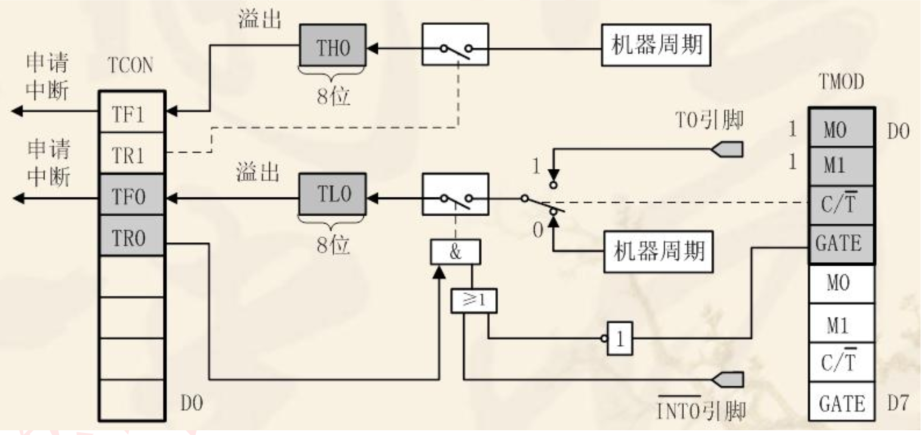
【51单片机】外部中断和定时器中断
目录 中断系统中断介绍中断概念 中断结构及相关寄存器中断结构中断相关寄存器 外部中断实验外部中断配置软件设计实验现象 定时器中断定时器介绍51 单片机定时器原理51 单片机定时/计数器结构51 单片机定时/计数器的工作方式 定时器配置硬件设计软件设计实验现象 中断系统 本章…...

零售行业供应商数据分发,怎样提高安全性和效率?
零售行业是我国经济发展的重要组成,零售行业包罗万象,如包括汽车零售、日化零售、快消品零售等,不同细分行业的运营模式各不相同,但大体来说,零售行业都具备最基础的供应商和零售商,供应商将商品或服务卖给…...
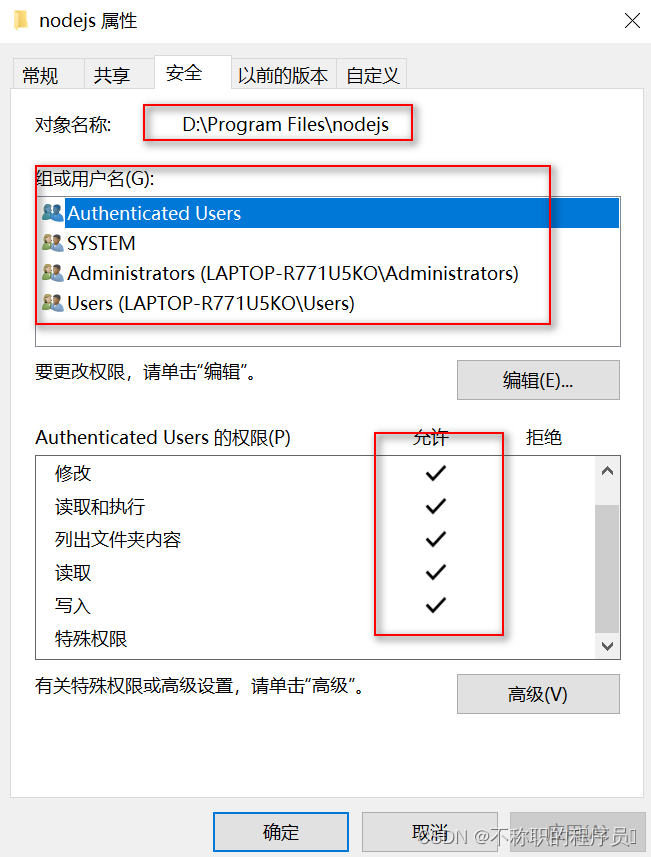
Windows下Node.js下载安装及环境变量配置教程
Windows下Node.js下载安装及环境变量配置教程 安装版本:node-v18.19.0-x64.msi 文章目录 Windows下Node.js下载安装及环境变量配置教程一、Node.js和NPM简介二、下载地址三、安装步骤四、环境配置五、安装淘宝镜像总结 一、Node.js和NPM简介 1、Node.js …...

广义表-C语言
广义表(Generalized List)是一种扩展了线性表的数据结构,它在线性表的基础上增加了元素可以是表的特点。在广义表中,元素不仅可以是单个的数据元素,还可以是一个子表,而子表中的元素也可以是数据元素或其他…...

uniapp+uView 【详解】录音,自制音频播放器
效果预览 代码实现 <template><view class"btnListBox"><view class"audioBox" v-if"audioLength"><u-row><u-col span"2"><u--text aligncenter :text"currentTime"></u--text>…...
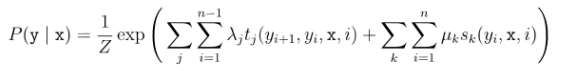
机器学习---概率图模型(隐马尔可夫模型、马尔可夫随机场、条件随机场)
1. 隐马尔可夫模型 机器学习最重要的任务是根据已观察到的证据(例如训练样本)对感兴趣的未知变量(例如类别标 记)进行估计和推测。概率模型(probabilistic model)提供了一种描述框架,将描述任…...

cool 框架 node 后端封装三方Api post请求函数
1.需求 现在一些数据源 ,需要从三方地址拿到一些数据 比如说电影列表 信息了 影院列表信息了 等一些展示的数据,但是人家这种东西 害需要使用 appkey appserect 这种验签 这种需求 你前端调用接口是直接调用不了的 因为需要用到验签 需要后端接口转接一…...

awd总结
总结: 由于是第一次参加AWD比赛,各方面经验都不足,在参赛的前几天也是疯狂搜集各种脚本、框架、工具等,同时也参考b站的视频进行学习,我发现就是还是实操才能更快的学习 我觉得就是我前期的准备工作不足,…...

【react】react+es6+antd5.13.2+ts,antd表格的操作如何在父组件写?
reactes6antd5.13.2ts,antd表格的操作如何在父组件写? 我的子组件columns.tsx,只加表头,操作放在父组件。 columns.tsx的代码: export const dataColumns [{title: 项目成员,dataIndex: name,key: name,},{title: 可选账号,alig…...

virtio笔记
最近在看虚拟化相关的东西,以virtio-console为例,记录下。 此文只是学习笔记,文中肯定有不少错误,不要参考 devicemd侧: virtio_console.c中,初始化会对port->cb赋值为 viritio_console_control_tx&am…...

初始web服务器(并基于idea来实现无需下载的tomcat)
前言 前面学习了对应的http协议,我们知道了他是在网络层进行数据传输的协议,负责相应数据以及接收数据的规则,但是在人员开发后端的时候不仅仅需要你写io流进行数据传输,还需要你进行对应的tcp协议来进行数据打包发送http协议-CSD…...
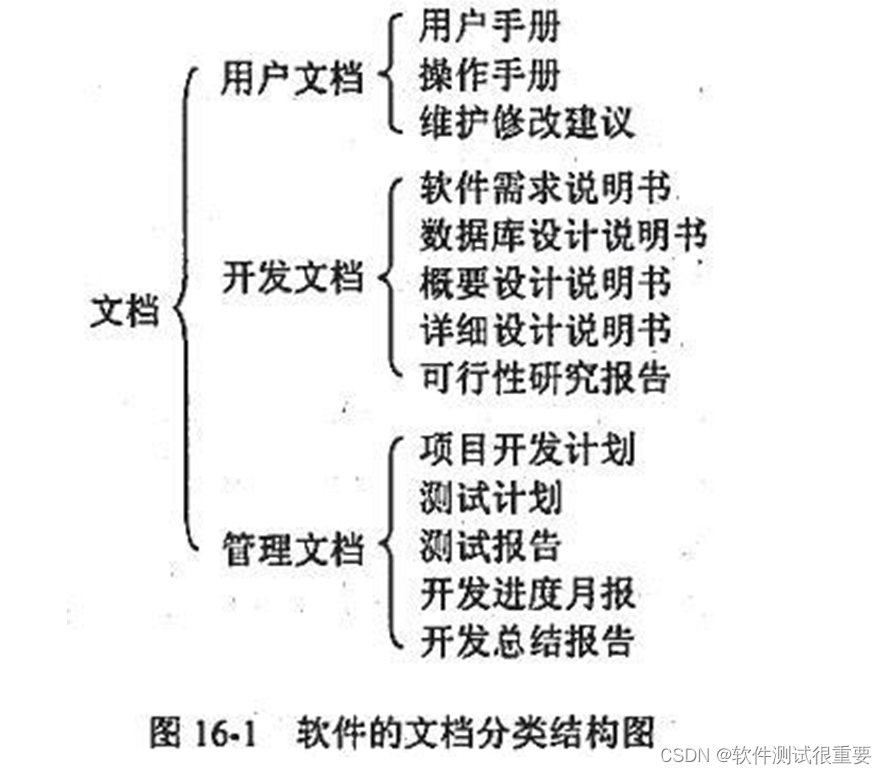
软件文档测试
1 文档测试的范围 软件产品由可运行的程序、数据和文档组成。文档是软件的一个重要组成部分。 在软件的整人生命周期中,会用到许多文档,在各个阶段中以文档作为前阶段工作成果的体现和后阶段工作的依据。 软件文档的分类结构图如下图所示: …...
从零开始手写mmo游戏从框架到爆炸(七)— 消息封装
导航:从零开始手写mmo游戏从框架到爆炸(零)—— 导航-CSDN博客 上一篇,我们初步把消息handler 注册到了服务中,在进行后续工作之前我们需要再做一些准备工作。 第一:把之前自己管理的bean放到spring中…...
)
从Unity到Three.js(画线组件line)
JavaScript 0基础,只是照着官方文档临摹了下,之后有时间再进行细节学习和功能封装。 import * as THREE from three; //引入threejsconst renderer new THREE.WebGLRenderer();//创建渲染器 //设置渲染范围,当前撑满全屏,屏幕左上角是&…...
)
LCP 30. 魔塔游戏 - 力扣(LeetCode)
题目描述 小扣当前位于魔塔游戏第一层,共有 N 个房间,编号为 0 ~ N-1。每个房间的补血道具/怪物对于血量影响记于数组 nums,其中正数表示道具补血数值,即血量增加对应数值;负数表示怪物造成伤害值,即血量减…...

数据结构——单向链表和双向链表的实现(C语言版)
目录 前言 1. 链表 1.1 链表的概念及结构 1.2 链表的分类 2. 单链表接口实现 2.1 数据结构设计与接口函数声明 2.2 创建结点,打印,查找 2.3 尾插,头插,尾删,头删 2.4 插入或删除 2.4.1在指定位置后 2.4.2在…...
(4)——4.使用TCP的协议有哪些?使用UDP的协议有哪些?)
TCP和UDP相关问题(重点)(4)——4.使用TCP的协议有哪些?使用UDP的协议有哪些?
4.使用TCP的协议有哪些?使用UDP的协议有哪些? 使用TCP的协议有:HTTP3.0之前的HTTP协议、HTTPS、FTP、SMTP、SSH... 使用UDP的协议有:HTTP3.0、DNS、DHCP......
Python进阶--爬取美女图片壁纸(基于回车桌面网的爬虫程序)
目录 一、前言 二、爬取下载美女图片 1、抓包分析 a、分析页面 b、明确需求 c、抓包搜寻 d、总结特点 2、编写爬虫代码 a、获取图片页网页源代码 b、提取所有图片的链接和标题 c、下载并保存这组图片 d、 爬取目录页的各种类型美女图片的链接 e、实现翻页 三、各…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
