算法沉淀——分治算法(leetcode真题剖析)

算法沉淀——分治算法
- 快排思想
- 01.颜色分类
- 02.排序数组
- 03.数组中的第K个最大元素
- 04.库存管理 III
- 归并思想
- 01.排序数组
- 02.交易逆序对的总数
- 03.计算右侧小于当前元素的个数
- 04.翻转对
分治算法是一种解决问题的算法范式,其核心思想是将一个大问题分解成若干个小问题,递归地解决这些小问题,最后将它们的解合并起来得到原问题的解。分治算法的一般步骤包括分解(Divide)、解决(Conquer)、合并(Combine)。
具体来说,分治算法包含以下几个步骤:
- 分解(Divide): 将原问题分解成若干个规模较小、相互独立的子问题。这一步通常是问题规模的减小或者数据规模的缩小。
- 解决(Conquer): 递归地解决这些子问题。对于规模较小的子问题,可以直接求解。
- 合并(Combine): 将子问题的解合并起来,得到原问题的解。
分治算法通常适用于能够被划分成相互独立子问题的问题,并且这些子问题的结构和原问题一样。经典的分治算法有许多,如归并排序、快速排序、二分搜索等。
经典例子:归并排序
- 分解(Divide): 将待排序的数组分成两半。
- 解决(Conquer): 对每个子数组进行归并排序,递归地进行排序。
- 合并(Combine): 合并已排序的子数组,得到最终的排序结果。
分治算法的优点包括:
- 模块化设计: 将问题分解成小问题,使得算法结构清晰,易于理解和实现。
- 可并行性: 分治算法通常适用于并行计算,因为子问题可以独立地求解。
- 适用范围广: 适用于一类问题,如排序、查找等。
快排思想
01.颜色分类
题目链接:https://leetcode.cn/problems/sort-colors/
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
提示:
n == nums.length1 <= n <= 300nums[i]为0、1或2
思路
具体的思路可以分为以下三个部分:
- 红色部分(0): 通过交换,保证红色元素的右边界
left的左侧都是红色元素。初始时,left设置为-1。 - 白色部分(1): 遍历过程中,遇到白色元素(1)时,直接将指针
i向右移动,不进行交换。白色元素已经排列在红色元素的右侧,所以不需要额外操作。 - 蓝色部分(2): 通过交换,保证蓝色元素的左边界
right的右侧都是蓝色元素。初始时,right设置为数组的长度。
整个过程在遍历指针 i 小于右边界 right 的情况下进行。当 i 与 right 相遇时,排序完成。
代码
class Solution {
public:void sortColors(vector<int>& nums) {for(int i=0,left=-1,right=nums.size();i<right;){if(nums[i]==0) swap(nums[++left],nums[i++]);else if(nums[i]==1) i++;else swap(nums[i],nums[--right]);}}
};
02.排序数组
题目链接:https://leetcode.cn/problems/sort-an-array/
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
思路
普通快排在这里是通过不了的,所以我们可以使用上面颜色分类的思想进行三路划分的优化
三路划分是对传统快速排序算法的一种改进,通过将数组划分为三个部分:小于、等于、大于基准值,从而在存在大量相同元素的情况下,提高了性能。
传统快速排序在处理有大量相同元素的数组时可能会导致不均匀的划分,使得递归树不平衡,进而影响性能。三路划分通过在划分过程中将数组分为小于、等于、大于基准值的三个部分,有效地解决了这一问题,具有以下优势:
- 减少重复元素的递归处理: 在存在大量相同元素的情况下,传统快速排序可能导致递归深度较大,而三路划分能够将相同元素聚集在一起,从而减少递归深度。
- 避免不必要的交换: 在传统快速排序中,可能会进行多次相同元素的交换,而三路划分通过将相同元素聚集在一起,避免了不必要的交换操作,提高了性能。
- 适用于含有大量重复元素的场景: 当数组中存在大量相同元素时,三路划分能够更好地利用重复元素的信息,提高排序效率。
三路划分的核心思想是通过一个循环,将数组划分为小于、等于、大于基准值的三个部分。这样,相同元素被聚集在等于基准值的部分,从而在递归过程中能够更高效地处理重复元素。这一优化使得算法在处理包含大量相同元素的数组时,性能更为稳定。
代码
class Solution {
public:int getRandom(vector<int>& nums,int left, int right){return nums[rand()%(right-left+1)+left];}void qsort(vector<int>& nums,int l, int r){if(l>=r) return;int key=getRandom(nums,l,r);int i=l,left=l-1,right=r+1;while(i<right){if(nums[i]<key) swap(nums[++left],nums[i++]);else if(nums[i]==key) i++;else swap(nums[--right],nums[i]);}qsort(nums,l,left);qsort(nums,right,r);}vector<int> sortArray(vector<int>& nums) {srand(time(NULL));qsort(nums,0,nums.size()-1);return nums;}
};
03.数组中的第K个最大元素
题目链接:https://leetcode.cn/problems/kth-largest-element-in-an-array/
给定整数数组 nums 和整数 k,请返回数组中第 **k** 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
思路
这里最常规的写法应该是使用堆排,但是这样达不到O(n)的时间复杂度,所以这里我们结合快排中的三路划分思想
代码
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand(time(NULL)); // 设置随机数种子return qsort(nums, 0, nums.size() - 1, k);}int qsort(vector<int>& nums, int l, int r, int k) {if (l == r) return nums[l];// 1. 随机选择基准元素int key = getRandom(nums, l, r);// 2. 根据基准元素将数组分为三块int left = l - 1, right = r + 1, i = l;while (i < right) {if (nums[i] < key) {swap(nums[++left], nums[i++]);} else if (nums[i] == key) {i++;} else {swap(nums[--right], nums[i]);}}// 3. 分情况讨论int c = r - right + 1, b = right - left - 1;if (c >= k) {// 第 k 大元素在右侧部分return qsort(nums, right, r, k);} else if (b + c >= k) {// 第 k 大元素等于基准元素return key;} else {// 第 k 大元素在左侧部分return qsort(nums, l, left, k - b - c);}}int getRandom(vector<int>& nums, int left, int right) {return nums[rand() % (right - left + 1) + left];}
};
- 计算左、右和基准三个部分的元素个数:
c表示右侧部分元素的个数,即大于基准元素的个数。b表示基准元素左侧部分元素的个数,即等于基准元素的个数。
- 判断第 k 大元素的位置:
- 如果右侧部分元素个数
c大于等于 k,说明第 k 大元素在右侧部分。因此,递归地在右侧部分中继续寻找第 k 大元素。 - 如果
b + c大于等于 k,说明第 k 大元素等于基准元素。此时,基准元素即为所求的第 k 大元素,直接返回基准元素的值。 - 如果以上两个条件都不满足,说明第 k 大元素在左侧部分。因此,递归地在左侧部分中继续寻找第 k 大元素,同时将
k减去右侧和基准元素的个数。
- 如果右侧部分元素个数
这样的划分和递归过程保证了在不同情况下都能正确地找到第 k 大元素,从而完成整个算法。这是随机化快速排序在选择第 k 大元素时的一种处理策略,通过考虑基准元素左右两侧的元素个数,提高了算法在寻找第 k 大元素时的效率。
04.库存管理 III
题目链接:https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof/
仓库管理员以数组 stock 形式记录商品库存表,其中 stock[i] 表示对应商品库存余量。请返回库存余量最少的 cnt 个商品余量,返回 顺序不限。
示例 1:
输入:stock = [2,5,7,4], cnt = 1
输出:[2]
示例 2:
输入:stock = [0,2,3,6], cnt = 2
输出:[0,2] 或 [2,0]
提示:
0 <= cnt <= stock.length <= 10000 0 <= stock[i] <= 10000
思路
这一题和上一题的思路基本一致,同样我们使用快速选择的算法,可以使时间复杂度达到O(n),只不过需要简单做一些调整
代码
class Solution {
public:void qsort(vector<int>& nums, int l, int r, int k) {if (l >= r) return;// 随机选择基准元素int key = nums[rand() % (r - l + 1) + l];int left = l - 1, right = r + 1, i = l;// 划分过程while (i < right) {if (nums[i] < key) {swap(nums[++left], nums[i++]);} else if (nums[i] == key) {i++;} else {swap(nums[--right], nums[i]);}}int a = left - l + 1, b = right - left - 1;// 根据划分情况递归处理if (a > k) {// 第 k 小元素在左侧部分qsort(nums, l, left, k);} else if (a + b >= k) {// 第 k 小元素在基准元素右侧,且可能包含部分基准元素return;} else {// 第 k 小元素在右侧部分qsort(nums, right, r, k - a - b);}}vector<int> inventoryManagement(vector<int>& stock, int cnt) {srand(time(NULL));// 调用随机化快速排序qsort(stock, 0, stock.size() - 1, cnt);// 返回前 cnt 小的商品return {stock.begin(), stock.begin() + cnt};}
};
归并思想
01.排序数组
题目链接:https://leetcode.cn/problems/sort-an-array/
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
思路
要理解分治中的归并思想,首先我们从归并排序入手,这里我直接编写代码,想看更清晰的排序剖析,可以翻看博主之前关于八大排序的博客
代码
class Solution {vector<int> tmp;
public:vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());mergeSort(nums, 0, nums.size() - 1);return nums;}void mergeSort(vector<int>& nums, int left, int right) {if (left >= right) return;// 计算中间位置int mid = (right + left) >> 1;// 递归对左右两部分进行归并排序mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);// 归并合并两个有序部分int cur1 = left, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= right)tmp[i++] = (nums[cur1] <= nums[cur2]) ? nums[cur1++] : nums[cur2++];while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= right) tmp[i++] = nums[cur2++];// 将归并后的结果拷贝回原数组for (int i = left; i <= right; ++i)nums[i] = tmp[i - left];}
};
02.交易逆序对的总数
题目链接:https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6]
输出:8
解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
限制:
0 <= record.length <= 50000
思路
这里我们使用归并的思想可以对数组边排序边进行逆序对的计算,我们在进行归并排序划分时,左边和右边都是相对有序的,我们在归并时,找到了左边相对右边大的那个数,就可以进行一次逆序对的组合,即此时左边被遍历的数及其之后的数都能和此时右边的数进行逆序匹配,此时我们累加逆序对的值,直到我们把整个数组归并完毕,逆序对的总数也就计算完毕了
代码
class Solution {int tmp[50000];
public:int reversePairs(vector<int>& record) {return mergeSort(record, 0, record.size() - 1);}int mergeSort(vector<int>& nums, int left, int right) {if (left >= right) return 0;int ret = 0;int mid = (left + right) >> 1;// 递归对左右两部分进行归并排序ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);// 归并合并两个有序部分,并统计逆序对个数int cur1 = left, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= right) {if (nums[cur1] <= nums[cur2]) {tmp[i++] = nums[cur1++];} else {ret += mid - cur1 + 1; // 统计逆序对个数tmp[i++] = nums[cur2++];}}while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= right) tmp[i++] = nums[cur2++];// 将归并后的结果拷贝回原数组for (int i = left; i <= right; ++i)nums[i] = tmp[i - left];return ret;}
};
03.计算右侧小于当前元素的个数
题目链接:https://leetcode.cn/problems/count-of-smaller-numbers-after-self/
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1]
输出:[0]
示例 3:
输入:nums = [-1,-1]
输出:[0,0]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
思路
我们可以继续利用上面的逆序对思想,只不过我们需要使用额外的数组来记录相对下标。
代码
class Solution {vector<int> ret;vector<int> index;int tmp[500000];int tindex[500000];
public:vector<int> countSmaller(vector<int>& nums) {int n=nums.size();ret.resize(n);index.resize(n);for(int i=0;i<n;i++) index[i]=i;mergeSort(nums,0,n-1);return ret;}void mergeSort(vector<int>& nums,int left,int right){if(left>=right) return;int mid=(left+right)>>1;mergeSort(nums,left,mid);mergeSort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=0;while(cur1<=mid&&cur2<=right){if(nums[cur1]<=nums[cur2]){tmp[i]=nums[cur2];tindex[i++]=index[cur2++];}else{ret[index[cur1]]+=right-cur2+1;tmp[i]=nums[cur1];tindex[i++]=index[cur1++];}}while(cur1<=mid){tmp[i]=nums[cur1];tindex[i++]=index[cur1++];}while(cur2<=right){tmp[i]=nums[cur2];tindex[i++]=index[cur2++];}for(int j=left;j<=right;j++){nums[j]=tmp[j-left];index[j]=tindex[j-left];}}
};
04.翻转对
题目链接:https://leetcode.cn/problems/reverse-pairs/
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个*重要翻转对*。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1]
输出: 2
示例 2:
输入: [2,4,3,5,1]
输出: 3
注意:
- 给定数组的长度不会超过
50000。 - 输入数组中的所有数字都在32位整数的表示范围内。
思路
总体思路依旧是使用归并,我们在每次排序前,找到当前的左边某个数大于右边的两倍,即可一次性计算该数后面的翻转对个数,数组排序完成,即可计算全部的翻转对
代码
class Solution {int tmp[50000];
public:int reversePairs(vector<int>& nums) {return mergeSort(nums,0,nums.size()-1);}int mergeSort(vector<int>& nums,int left,int right){if(left>=right) return 0;int ret=0;int mid=(left+right)>>1;ret+=mergeSort(nums,left,mid);ret+=mergeSort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=left;while(cur1<=mid){while(cur2<=right&&nums[cur2]>=nums[cur1]/2.0) cur2++;if(cur2>right) break;ret+=right-cur2+1;cur1++;}cur1=left,cur2=mid+1;while(cur1<=mid&&cur2<=right) tmp[i++]=nums[cur1]<=nums[cur2]?nums[cur2++]:nums[cur1++];while(cur1<=mid) tmp[i++]=nums[cur1++];while(cur2<=right) tmp[i++]=nums[cur2++];for(int j=left;j<=right;j++)nums[j]=tmp[j];return ret;}
};
相关文章:

算法沉淀——分治算法(leetcode真题剖析)
算法沉淀——分治算法 快排思想01.颜色分类02.排序数组03.数组中的第K个最大元素04.库存管理 III 归并思想01.排序数组02.交易逆序对的总数03.计算右侧小于当前元素的个数04.翻转对 分治算法是一种解决问题的算法范式,其核心思想是将一个大问题分解成若干个小问题&a…...

Qt 进程守护程序
Qt 进程守护程序 简单粗暴的监控,方法可整合到其他代码。 一、windows环境下 1、进程查询函数 processCount函数用于查询系统所有运行的进程中该进程运行的数量,比如启动了5个A进程,该函数查询返回的结果就为5。 windows下使用了API接口查询…...
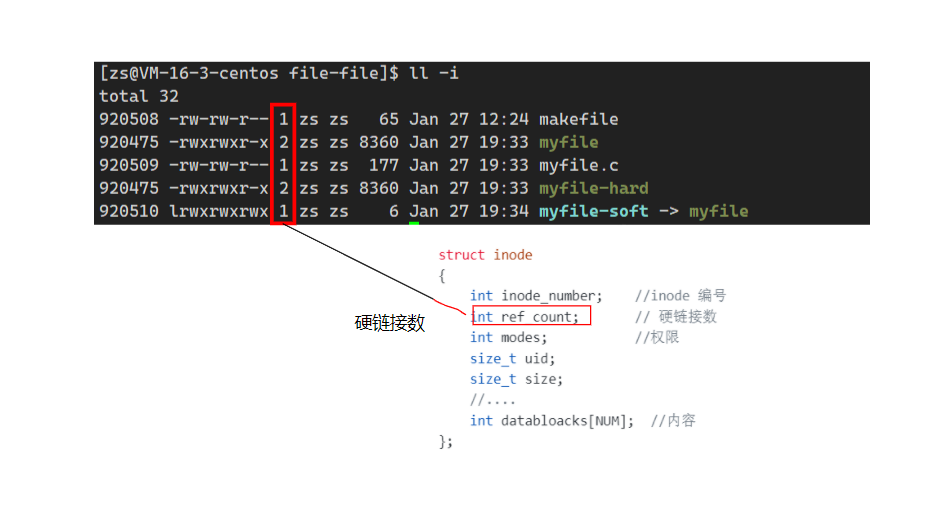
Linux_文件系统
假定外部存储设备为磁盘,文件如果没有被使用,那么它静静躺在磁盘上,如果它被使用,则文件将被加载进内存中。故此,可以将文件分为内存文件和磁盘文件。 内存文件 磁盘文件 软、硬链接 一.内存文件 1.1 c语言的文件接口 …...
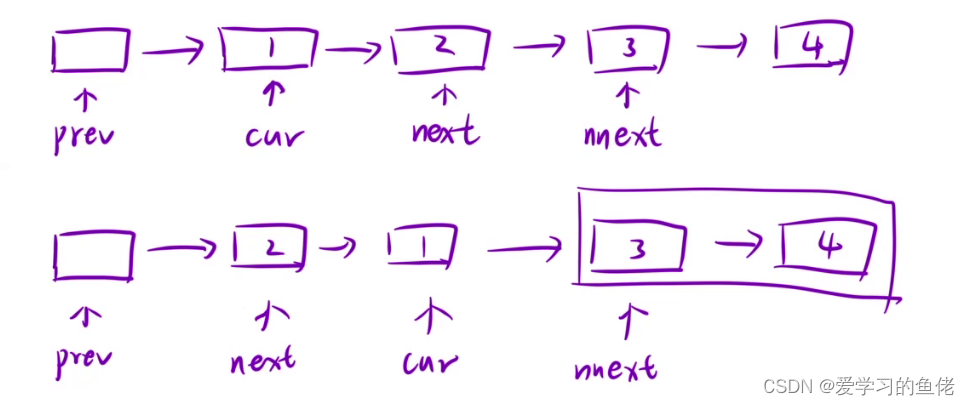
算法沉淀——链表(leetcode真题剖析)
算法沉淀——链表 01.两数相加02.两两交换链表中的节点03.重排链表04.合并 K 个升序链表05.K个一组翻转链表 链表常用技巧 1、画图->直观形象、便于理解 2、引入虚拟"头节点" 3、要学会定义辅助节点(比如双向链表的节点插入) 4、快慢双指针…...

Flink从入门到实践(一):Flink入门、Flink部署
文章目录 系列文章索引一、快速上手1、导包2、求词频demo(1)要读取的数据(2)demo1:批处理(离线处理)(3)demo2 - lambda优化:批处理(离线处理&…...

python分离字符串 2022年12月青少年电子学会等级考试 中小学生python编程等级考试二级真题答案解析
目录 python分离字符串 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序代码 四、程序说明 五、运行结果 六、考点分析 七、 推荐资料 1、蓝桥杯比赛 2、考级资料 3、其它资料 python分离字符串 2022年12月 python编程等级考试级编程题 一、题目要…...
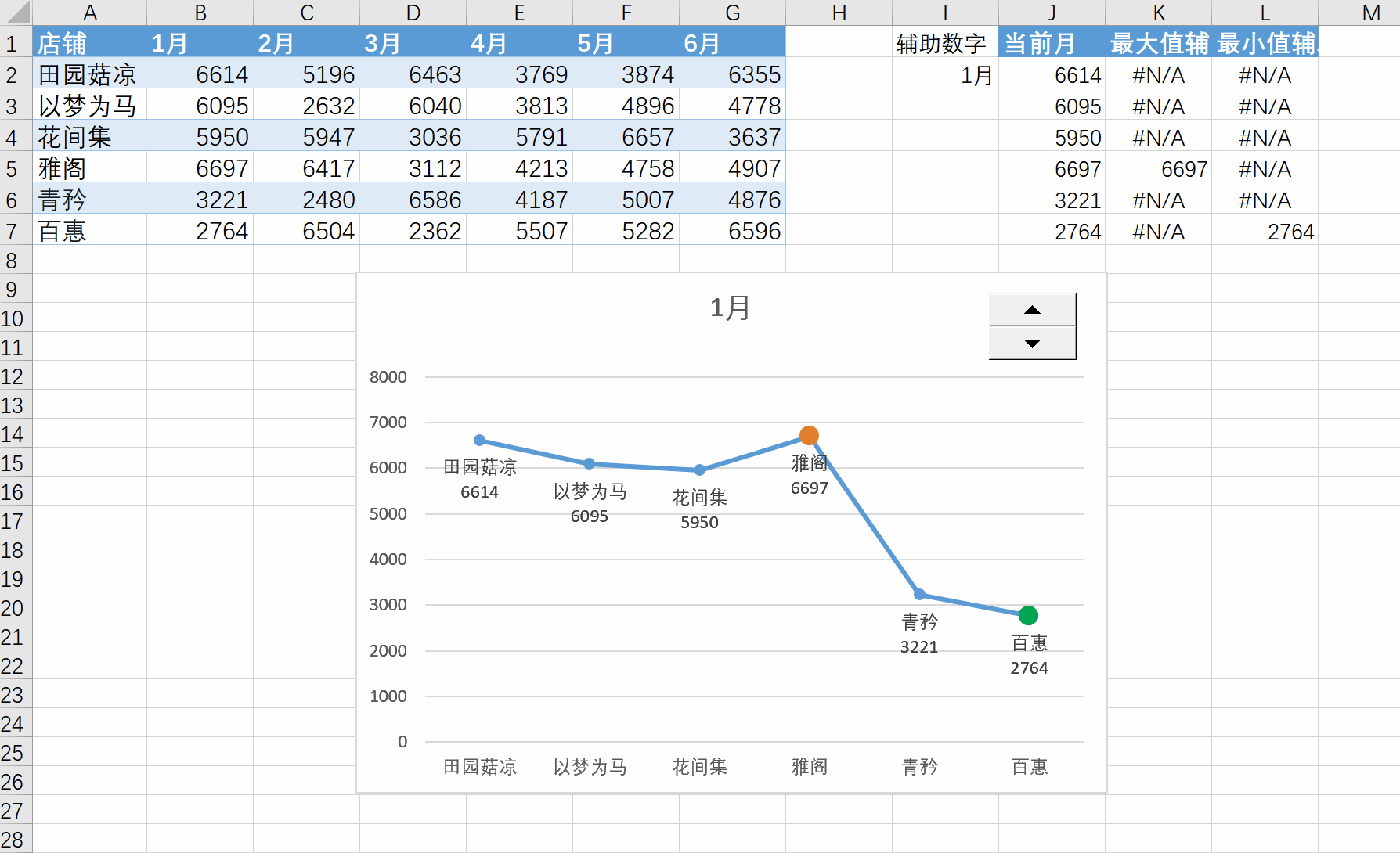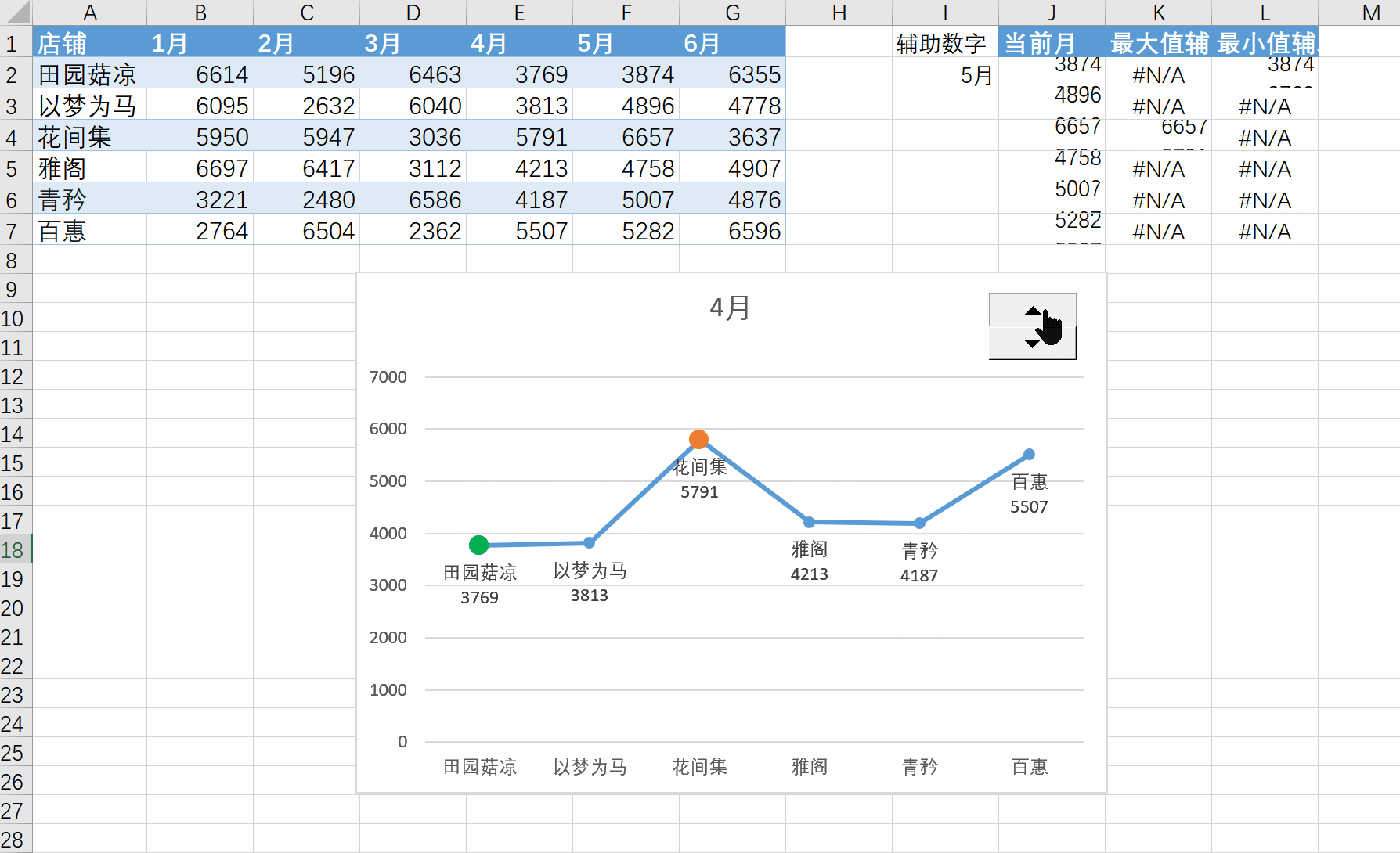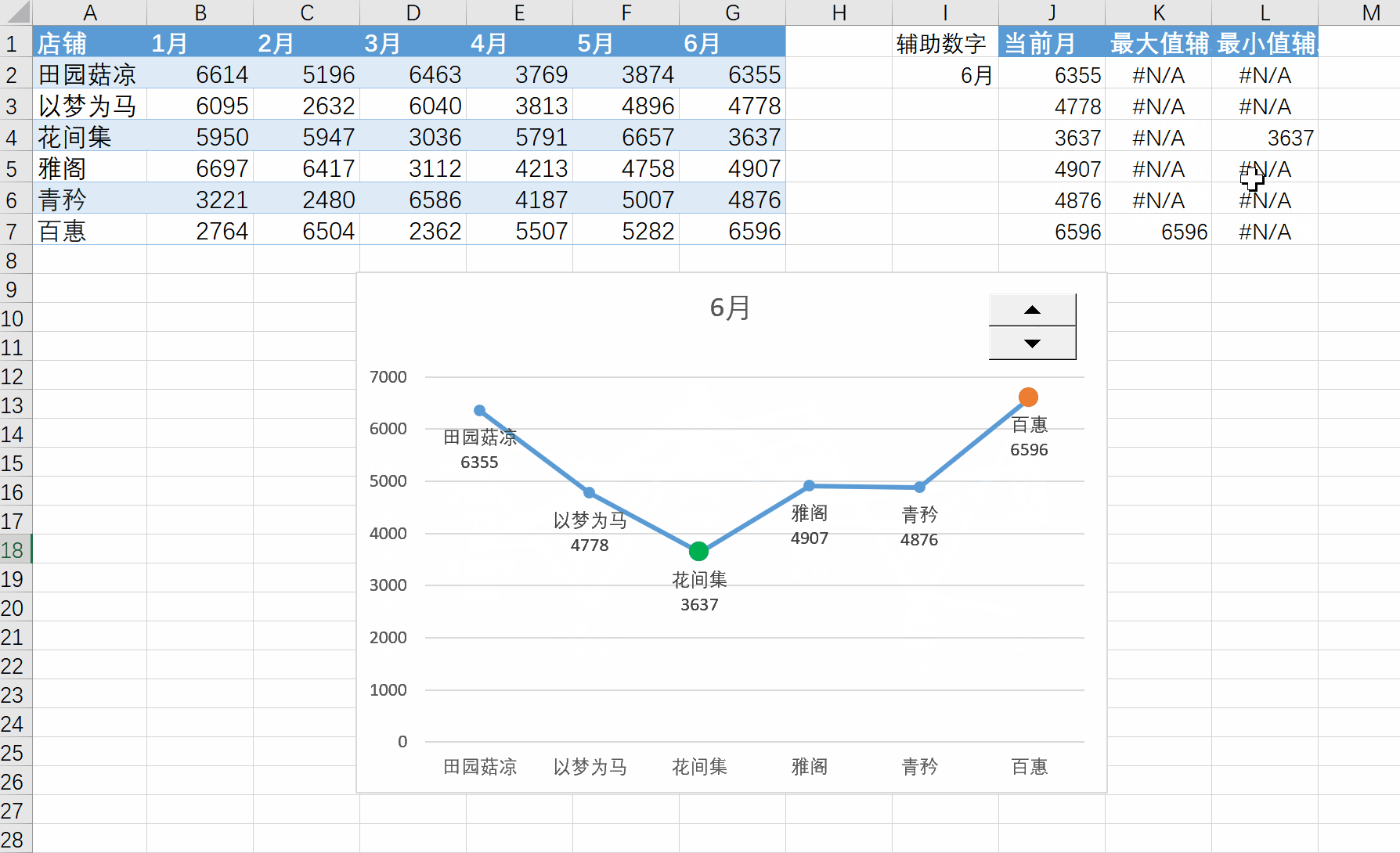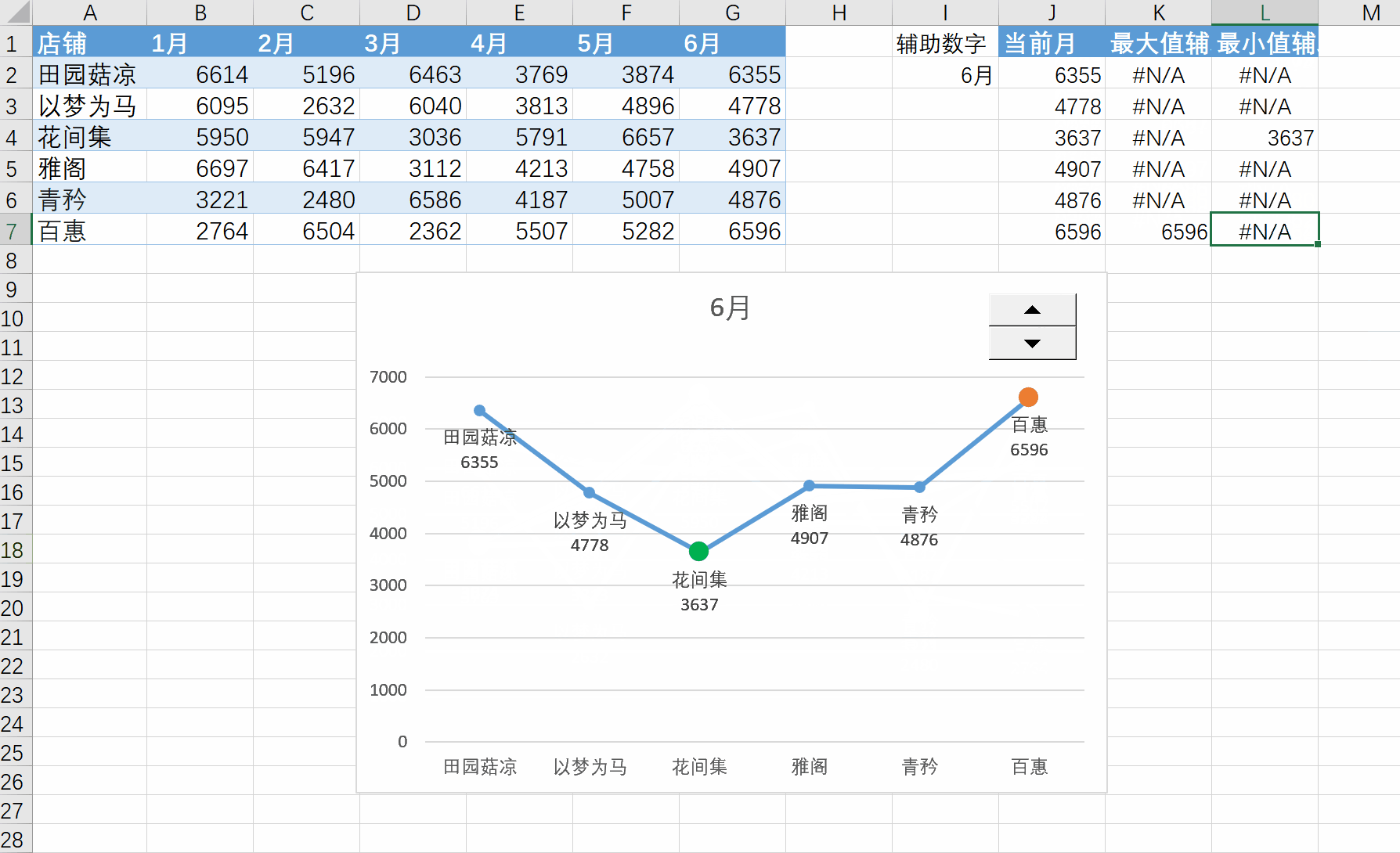
Excel练习:折线图突出最大最小值
Excel练习:折线图突出最大最小值 要点:NA值在折现图中不会被绘制,看似一条线,实际是三条线。换成0值和""都不行。 查看所有已分享Excel文件-阿里云 学习的这个视频:Excel折线图,…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之MenuItem组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之MenuItem组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、MenuItem组件 用来展示菜单Menu中具体的item菜单项。 子组件 无。 接口 Men…...

Mockito测试框架中的方法详解
这里写目录标题 第一章、模拟对象1.1)①mock()方法:1.2)②spy()方法: 第二章、模拟对象行为2.1)模拟方法调用①when()方法 2.2)模拟返回值②thenReturn(要返回的值)③doReturn() 2.3)模拟并替换…...

Atcoder ABC339 A - TLD
TLD 时间限制:2s 内存限制:1024MB 【原题地址】 所有图片源自Atcoder,题目译文源自脚本Atcoder Better! 点击此处跳转至原题 【问题描述】 【输入格式】 【输出格式】 【样例1】 【样例输入1】 atcoder.jp【样例输出1】 jp【样例说明…...

企业级DevOps实战
第1章 Zookeeper服务及MQ服务 Zookeeper(动物管理员)是一个开源的分布式协调服务,目前由Apache进行维护。 MQ概念 MQ(消息队列)是一种应用程序之间的通信方法,应用程序通过读写出入队列的消息࿰…...

C++中的new和delete
1.new和delete的语法 我们知道C语言的内存管理方式是malloc、calloc、realloc和free,而我们的C中除了可以使用这些方式之外还可以选择使用new和delete来进行内存管理。 new和delete的主要语法如下 从上面的代码我们只能知道new要比malloc好写一些,但是其…...

rtt设备io框架面向对象学习-dac设备
目录 1.dac设备基类2.dac设备基类的子类3.初始化/构造流程3.1设备驱动层3.2 设备驱动框架层3.3 设备io管理层 4.总结5.使用 1.dac设备基类 此层处于设备驱动框架层。也是抽象类。 在/ components / drivers / include / drivers 下的dac.h定义了如下dac设备基类 struct rt_da…...
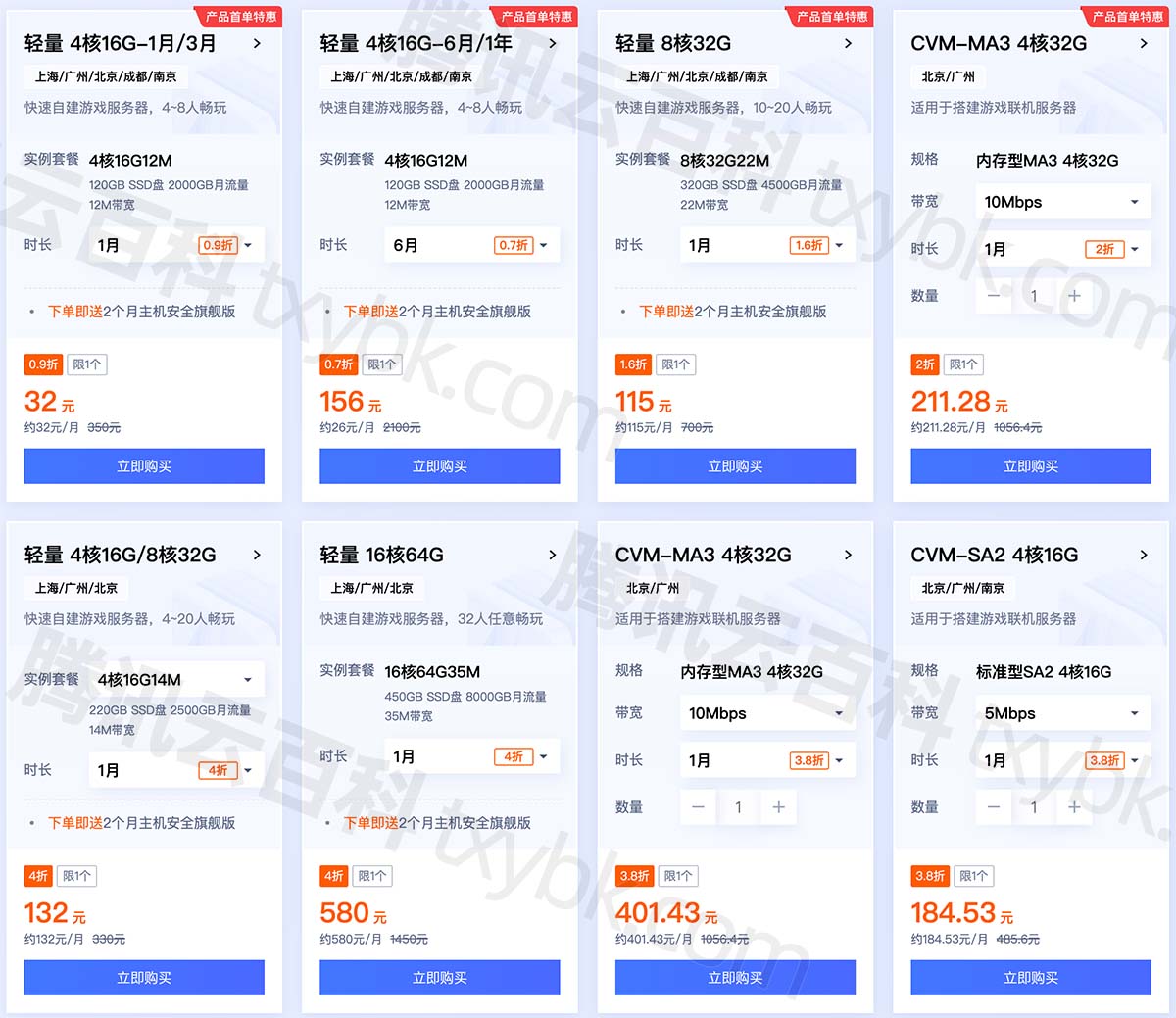
腾讯云幻兽帕鲁服务器配置怎么选择合适?
腾讯云幻兽帕鲁服务器配置怎么选?根据玩家数量选择CPU内存配置,4到8人选择4核16G、10到20人玩家选择8核32G、2到4人选择4核8G、32人选择16核64G配置,腾讯云百科txybk.com来详细说下腾讯云幻兽帕鲁专用服务器CPU内存带宽配置选择方法ÿ…...

796. 子矩阵的和
Problem: 796. 子矩阵的和 文章目录 思路解题方法复杂度Code 思路 这是一个二维前缀和的问题。二维前缀和的主要思想是预处理出一个二维数组,使得每个位置(i, j)上的值表示原数组中从(0, 0)到(i, j)形成的子矩阵中所有元素的和。这样,对于任意的子矩阵(x…...

如何在 Python 中处理 Unicode
介绍 Unicode 是世界上大多数计算机的标准字符编码。它确保文本(包括字母、符号、表情符号,甚至控制字符)在不同设备、平台和数字文档中显示一致,无论使用的操作系统或软件是什么。它是互联网和计算机行业的重要组成部分…...

CSDN文章导出PDF整理状况一览
最近CSDN有了导出文章PDF功能,导出的PDF还可以查询, 因此,把文章导出PDF,备份一下自己的重要资料。 目前整理内容如下 No.文章标题整理时间整理之后 文章更新Size (M)10001_本地电脑-开发相关软件保持位…...
)
jmeter-05变量(用户定义变量,用户参数,csv文档参数化)
文章目录 一、jmeter有三种变量二、用户定义变量(这个更多的可以理解为全局变量)1、设置2、引用三、用户参数(可以理解为局部变量)1、设置2、引用3、用户参数化要配合线程组的线程数使用4、结果五、csv文档参数1、创建csv文件2、设置2、引用csv文件可以配合线程组的线程数,…...

CSS之水平垂直居中
如何实现一个div的水平垂直居中 <div class"content-wrapper"><div class"content">content</div></div>flex布局 .content-wrapper {width: 400px;height: 400px;background-color: lightskyblue;display: flex;justify-content:…...

2.8日学习打卡----初学RabbitMQ(三)
2.8日学习打卡 一.springboot整合RabbitMQ 之前我们使用原生JAVA操作RabbitMQ较为繁琐,接下来我们使用 SpringBoot整合RabbitMQ,简化代码编写 创建SpringBoot项目,引入RabbitMQ起步依赖 <!-- RabbitMQ起步依赖 --> <dependency&g…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
