备战蓝桥杯---图论基础理论
图的存储:
1.邻接矩阵:

我们用map[i][j]表示i--->j的边权
2.用vector数组(在搜索专题的游戏一题中应用过)
3.用邻接表:
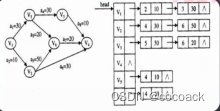 下面是用链表实现的基本功能的代码:
下面是用链表实现的基本功能的代码:
#include<bits/stdc++.h>
using namespace std;
struct node{int dian,zhi;struct node* next;
};
void insert(int x,int y,int z){node *p=new node;p->dian=y;p->zhi=z;p->next=head[x];head[x]=p;
}4.用伪邻接表(链式前向星)(注意第一个next=-1,开始直接memset head=-1即可)
对于(1,3,30,-1)表示1的点指向3,边权为30,下一条边.
我们把这个存在edge[1]里,并令head[1]=1;
(3,6,10,-1),我们存在edge[2]里,并令head[3]=2;
(1,2,10,head[1]),我们存在edge【3】里,并让head[1]=3;
下面是实现的代码:
#include<bits/stdc++.h>
using namespace std;
struct node{int dian,zhi;int next;
};
void insert(int x,int y,int z){edge[++m].dian=y;edge[m].zhi=z;edge[m].next=head[x];head[x]=m;
}欧拉图(前提是联通)
如果图的一个路径包括每个边恰好一次,则为欧拉路径。
欧拉路径+回路=欧拉回路。
具有欧拉回路的图为欧拉图,具有欧拉路径但无欧拉回路的图为半欧拉图
那么如何判断是否为欧拉图呢?
对于无向图,等价于该图所有顶点的度数为偶数(一进一出)+联通。
对于有向图,等价于该图所有顶点的入度==出度+联通。
拓扑排序
即按照一定的规则安排活动的先后次序(可能有多解)。
现在给一张图,a--》b表示要完成b必须先完成a,那我们如何排序呢?
1.先找没有前驱的点作为开始。
2.把它连着的边给删除,产生更多没有前驱的点作为下一步,入度-1。
3.删不动则无法完成。
具体实现中,我们不能总是去跑入度为0的点。
于是,我们用一个队列。在删后发现入度为0的点就放入队列中即可。
下面是实现的代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
struct node{int dian;int next;
}edge[1000000];
int head[1010],inc[1010];
queue<int> q;
void insert(int x,int y){edge[++cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
void tuopu(){for(int i=1;i<=n;i++){if(inc[i]==0) q.push(i);}int tot=0;while(!q.empty()){int x=q.front();q.pop();cout<<x<<endl;tot++;for(int i=head[x];i!=-1;i=edge[i].next){inc[edge[i].dian]--;if(inc[edge[i].dian]==0){q.push(edge[i].dian);}}}if(tot!=n) cout<<-1;
}
int main(){cin>>n>>m;memset(head,-1,sizeof(head));for(int i=1;i<=m;i++){int x,y;cin>>x>>y;insert(x,y);inc[y]++;}tuopu();
}拓扑排序的应用:
1.判断一个有向图是否有环,无环的图所有点都可以拓扑排序。
2.AOE网:


对于第一个,我们只用在拓扑排序上维护时间的max即可。
对于第二个,我们可以计算一下每一个活动的最早开始时间与最晚开始时间,因此我们相当于求最早开始时间等于最晚开始时间的点。
那么,我们如何求最晚开始时间呢?
我们只要从结尾反方向跑一回即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
struct node{int dian;int next;int zhi;
}edge[1000000];
int head[1010],inc[1010],shijian[1010];
queue<int> q;
void insert(int x,int y,int z){edge[++cnt].dian=y;edge[cnt].next=head[x];edge[cnt].zhi=z;head[x]=cnt;
}
void tuopu(){for(int i=1;i<=n;i++){if(inc[i]==0){q.push(i);shijian[i]=0;}}while(!q.empty()){int x=q.front();q.pop();for(int i=head[x];i!=-1;i=edge[i].next){inc[edge[i].dian]--;shijian[edge[i].dian]=max(shijian[edge[i].dian],shijian[x]+edge[i].zhi);if(inc[edge[i].dian]==0){q.push(edge[i].dian);}}}
}
int main(){cin>>n>>m;memset(head,-1,sizeof(head));for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;insert(x,y,z);inc[y]++;}tuopu();cout<<shijian[n];
}相关文章:

备战蓝桥杯---图论基础理论
图的存储: 1.邻接矩阵: 我们用map[i][j]表示i--->j的边权 2.用vector数组(在搜索专题的游戏一题中应用过) 3.用邻接表: 下面是用链表实现的基本功能的代码: #include<bits/stdc.h> using nam…...

[office] excel2003进行可视性加密的方法 #媒体#其他#知识分享
excel2003进行可视性加密的方法 Excel如何对重要文件进行可视性的加密处理呢?下面是小编带来的关于excel2003进行可视性加密的方法,希望阅读过后对你有所启发! excel2003进行可视性加密的方法: 可视性加密步骤1:打开你要加密的excel2003文档…...

算法沉淀——分治算法(leetcode真题剖析)
算法沉淀——分治算法 快排思想01.颜色分类02.排序数组03.数组中的第K个最大元素04.库存管理 III 归并思想01.排序数组02.交易逆序对的总数03.计算右侧小于当前元素的个数04.翻转对 分治算法是一种解决问题的算法范式,其核心思想是将一个大问题分解成若干个小问题&a…...

Qt 进程守护程序
Qt 进程守护程序 简单粗暴的监控,方法可整合到其他代码。 一、windows环境下 1、进程查询函数 processCount函数用于查询系统所有运行的进程中该进程运行的数量,比如启动了5个A进程,该函数查询返回的结果就为5。 windows下使用了API接口查询…...
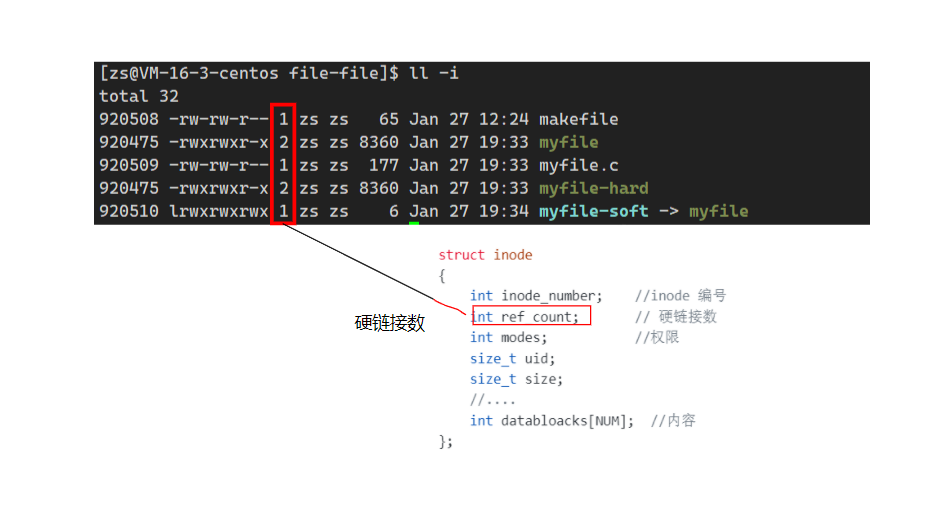
Linux_文件系统
假定外部存储设备为磁盘,文件如果没有被使用,那么它静静躺在磁盘上,如果它被使用,则文件将被加载进内存中。故此,可以将文件分为内存文件和磁盘文件。 内存文件 磁盘文件 软、硬链接 一.内存文件 1.1 c语言的文件接口 …...
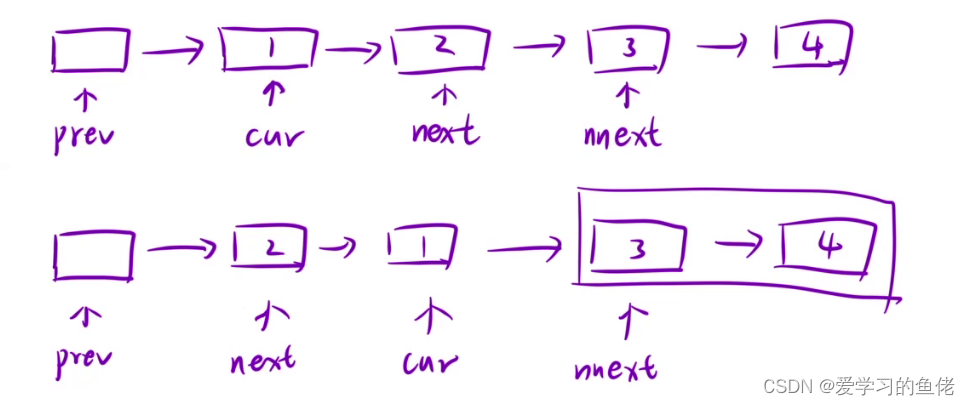
算法沉淀——链表(leetcode真题剖析)
算法沉淀——链表 01.两数相加02.两两交换链表中的节点03.重排链表04.合并 K 个升序链表05.K个一组翻转链表 链表常用技巧 1、画图->直观形象、便于理解 2、引入虚拟"头节点" 3、要学会定义辅助节点(比如双向链表的节点插入) 4、快慢双指针…...

Flink从入门到实践(一):Flink入门、Flink部署
文章目录 系列文章索引一、快速上手1、导包2、求词频demo(1)要读取的数据(2)demo1:批处理(离线处理)(3)demo2 - lambda优化:批处理(离线处理&…...

python分离字符串 2022年12月青少年电子学会等级考试 中小学生python编程等级考试二级真题答案解析
目录 python分离字符串 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序代码 四、程序说明 五、运行结果 六、考点分析 七、 推荐资料 1、蓝桥杯比赛 2、考级资料 3、其它资料 python分离字符串 2022年12月 python编程等级考试级编程题 一、题目要…...
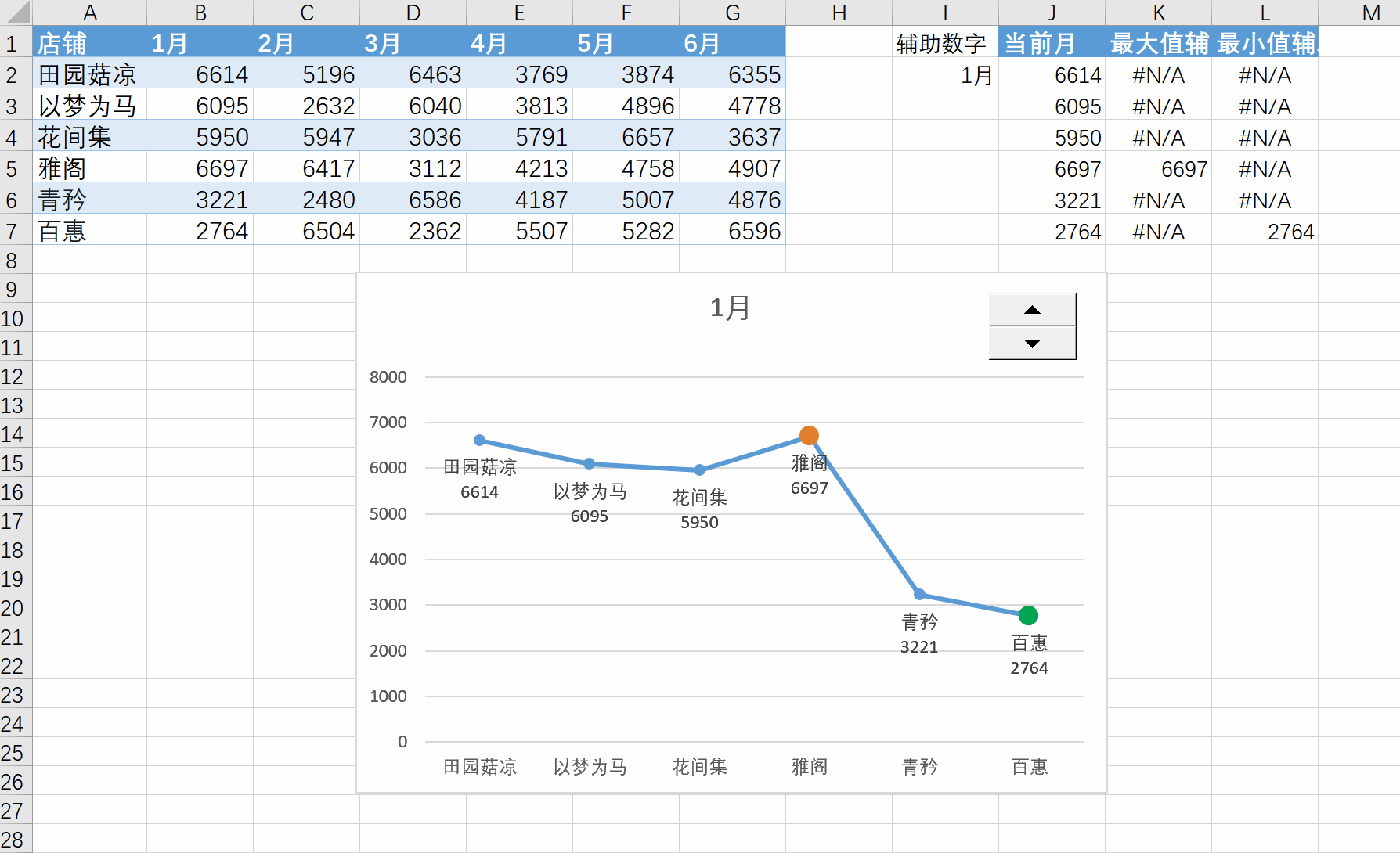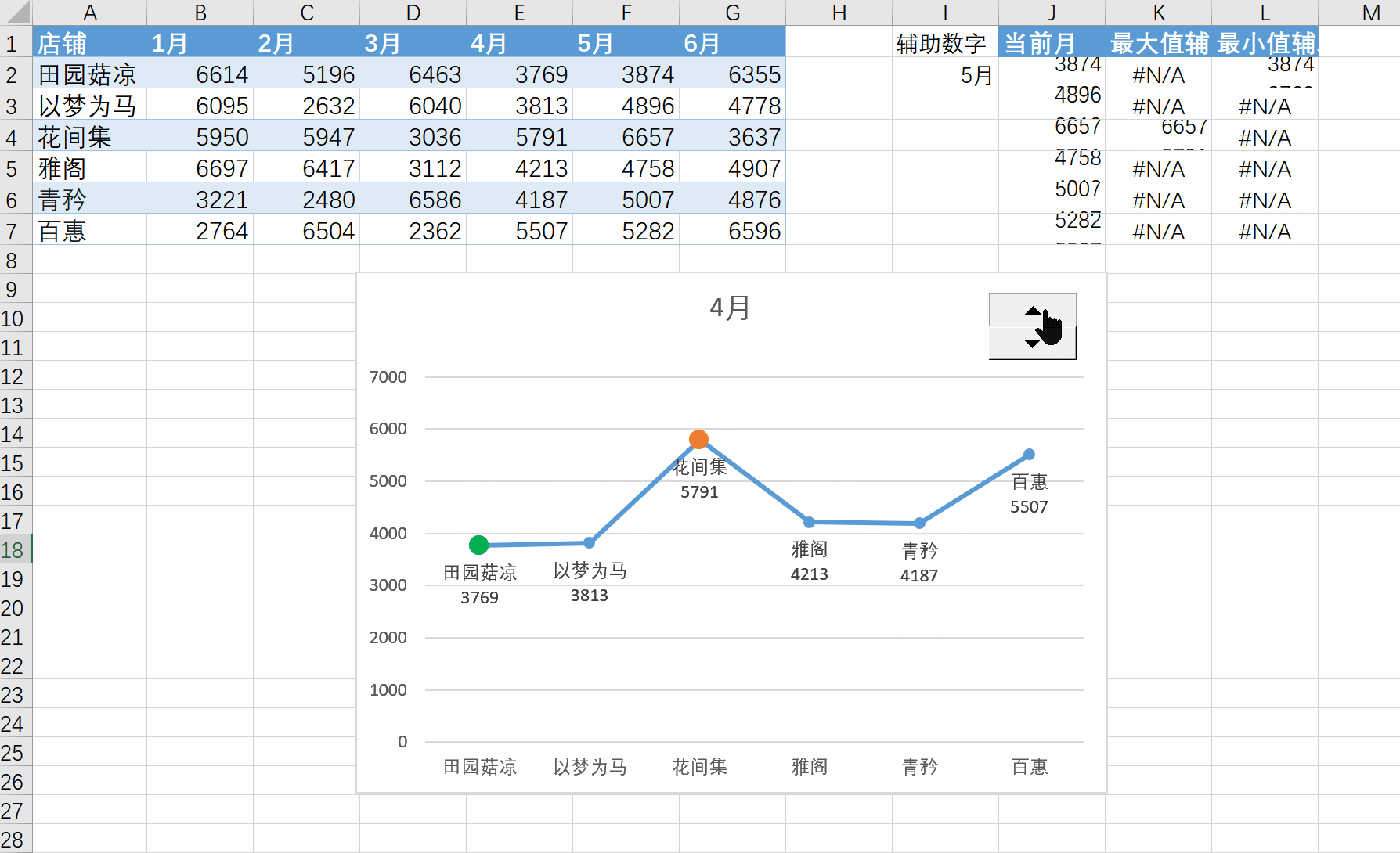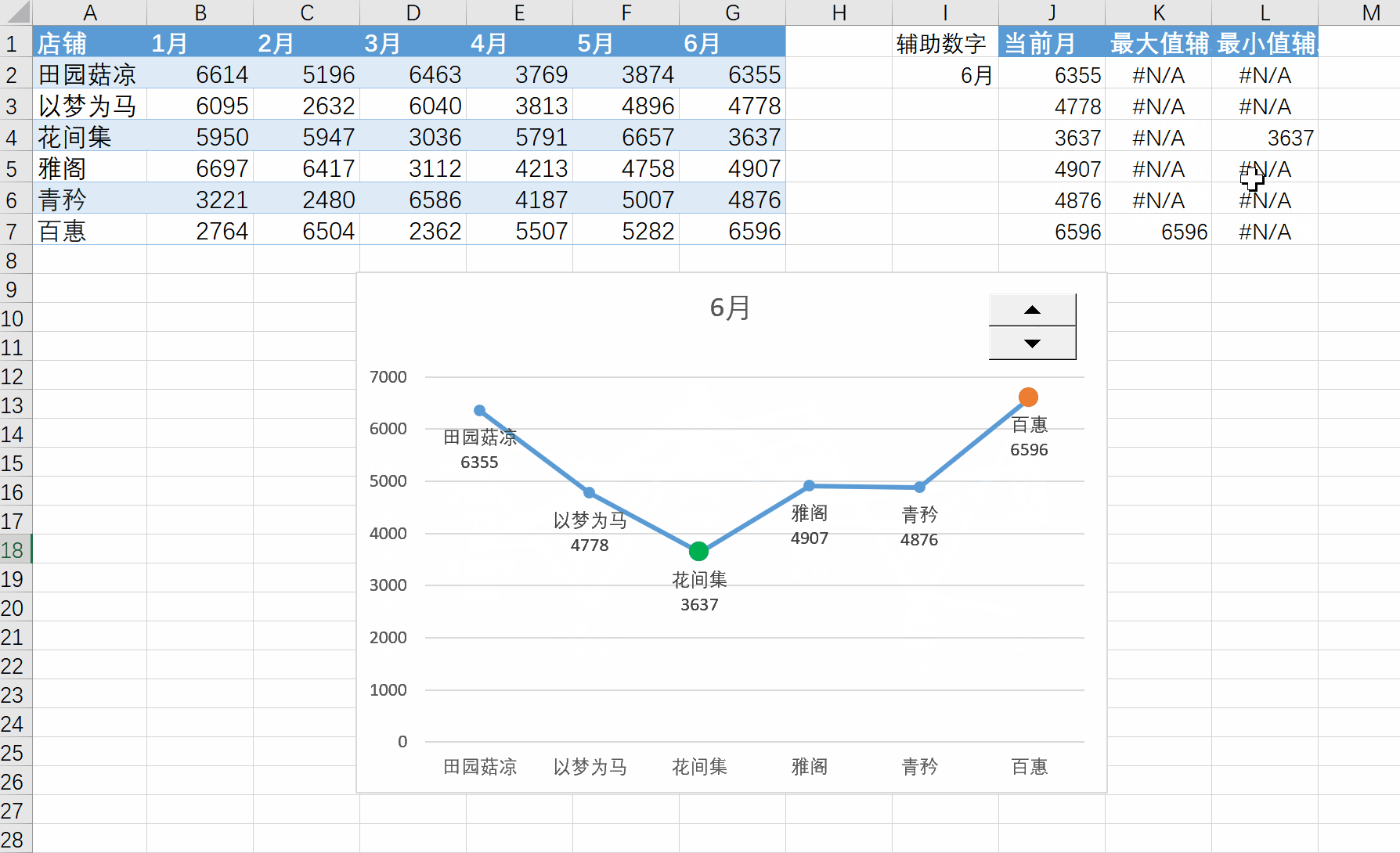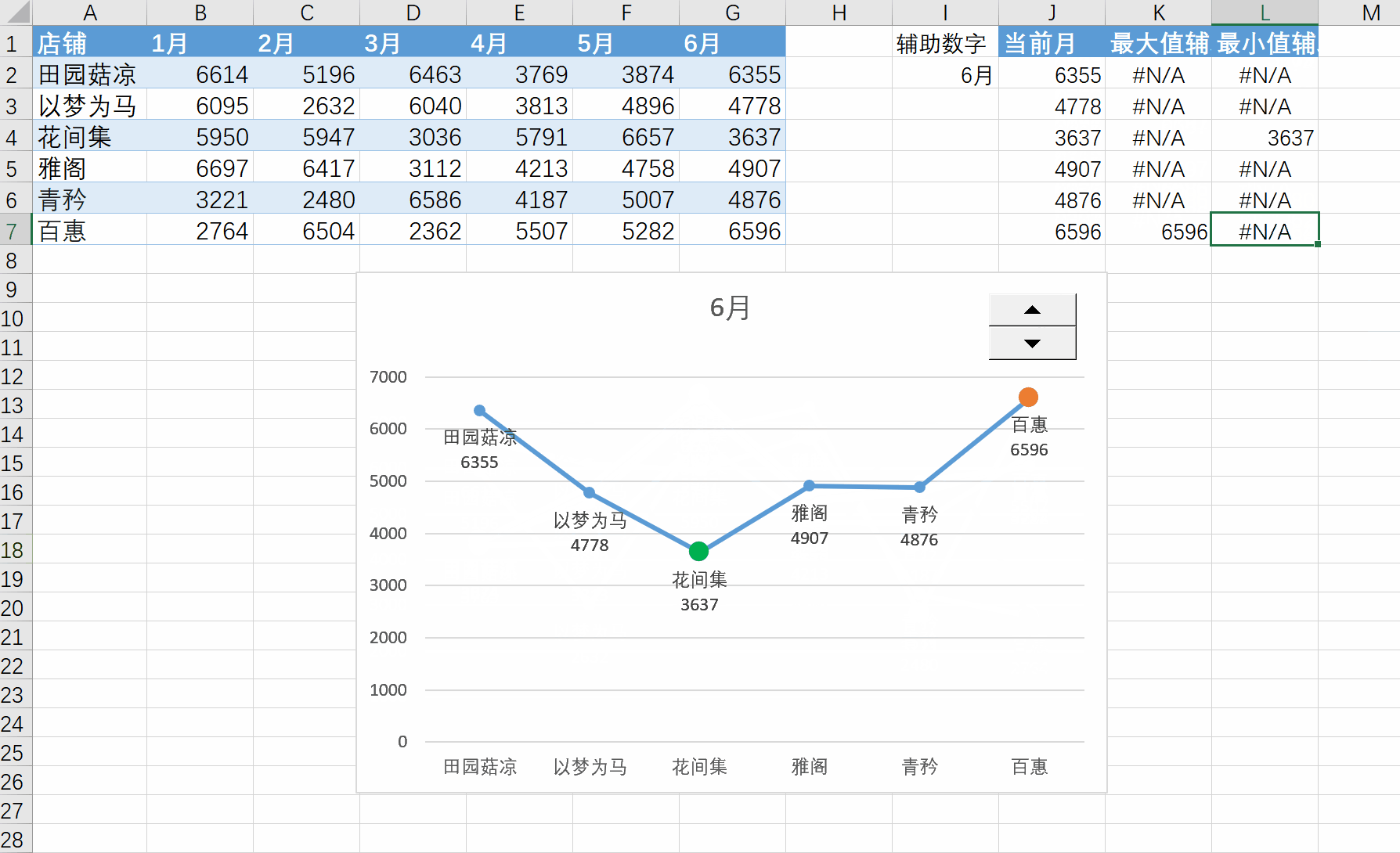
Excel练习:折线图突出最大最小值
Excel练习:折线图突出最大最小值 要点:NA值在折现图中不会被绘制,看似一条线,实际是三条线。换成0值和""都不行。 查看所有已分享Excel文件-阿里云 学习的这个视频:Excel折线图,…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之MenuItem组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之MenuItem组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、MenuItem组件 用来展示菜单Menu中具体的item菜单项。 子组件 无。 接口 Men…...

Mockito测试框架中的方法详解
这里写目录标题 第一章、模拟对象1.1)①mock()方法:1.2)②spy()方法: 第二章、模拟对象行为2.1)模拟方法调用①when()方法 2.2)模拟返回值②thenReturn(要返回的值)③doReturn() 2.3)模拟并替换…...

Atcoder ABC339 A - TLD
TLD 时间限制:2s 内存限制:1024MB 【原题地址】 所有图片源自Atcoder,题目译文源自脚本Atcoder Better! 点击此处跳转至原题 【问题描述】 【输入格式】 【输出格式】 【样例1】 【样例输入1】 atcoder.jp【样例输出1】 jp【样例说明…...

企业级DevOps实战
第1章 Zookeeper服务及MQ服务 Zookeeper(动物管理员)是一个开源的分布式协调服务,目前由Apache进行维护。 MQ概念 MQ(消息队列)是一种应用程序之间的通信方法,应用程序通过读写出入队列的消息࿰…...

C++中的new和delete
1.new和delete的语法 我们知道C语言的内存管理方式是malloc、calloc、realloc和free,而我们的C中除了可以使用这些方式之外还可以选择使用new和delete来进行内存管理。 new和delete的主要语法如下 从上面的代码我们只能知道new要比malloc好写一些,但是其…...

rtt设备io框架面向对象学习-dac设备
目录 1.dac设备基类2.dac设备基类的子类3.初始化/构造流程3.1设备驱动层3.2 设备驱动框架层3.3 设备io管理层 4.总结5.使用 1.dac设备基类 此层处于设备驱动框架层。也是抽象类。 在/ components / drivers / include / drivers 下的dac.h定义了如下dac设备基类 struct rt_da…...
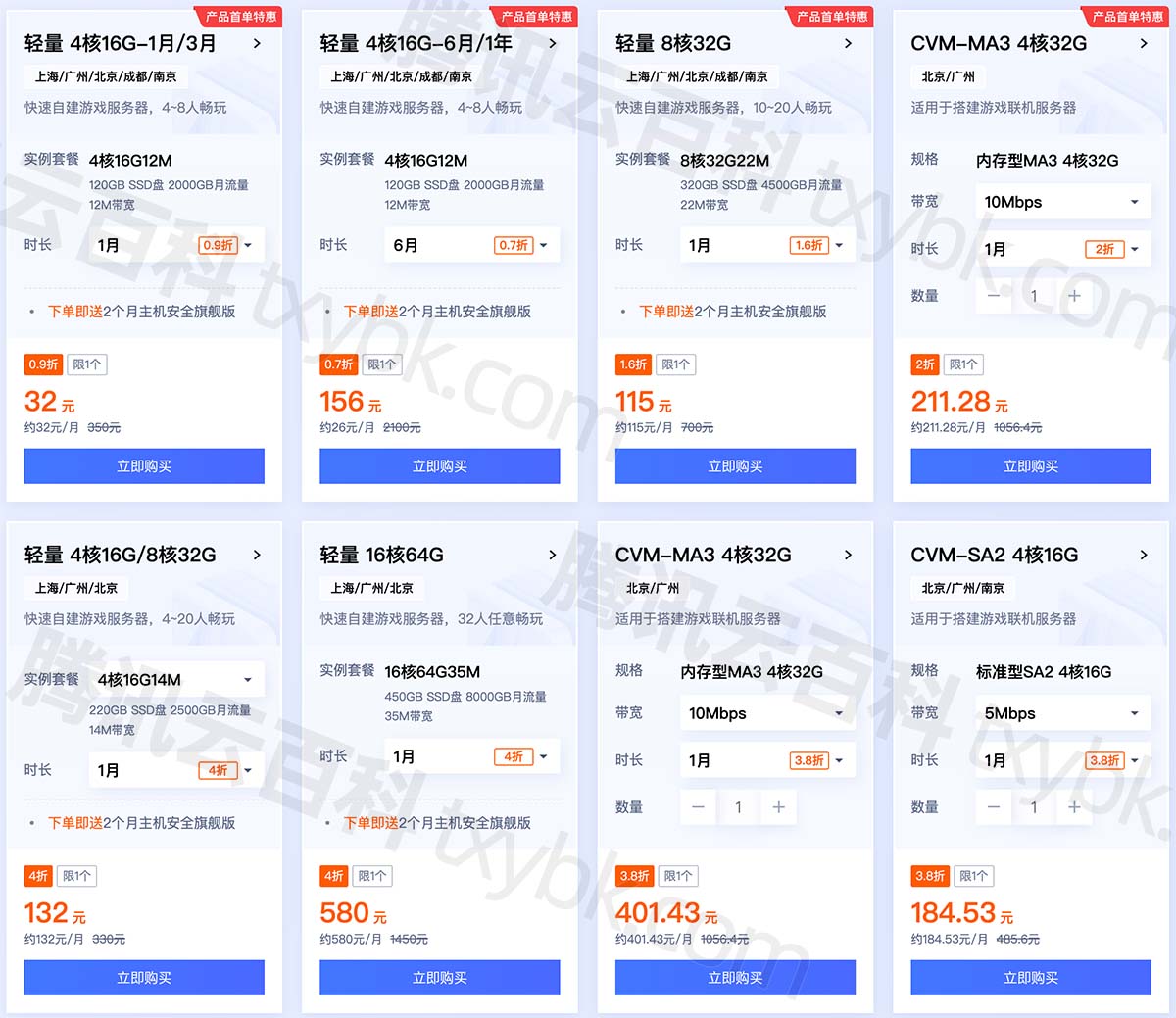
腾讯云幻兽帕鲁服务器配置怎么选择合适?
腾讯云幻兽帕鲁服务器配置怎么选?根据玩家数量选择CPU内存配置,4到8人选择4核16G、10到20人玩家选择8核32G、2到4人选择4核8G、32人选择16核64G配置,腾讯云百科txybk.com来详细说下腾讯云幻兽帕鲁专用服务器CPU内存带宽配置选择方法ÿ…...

796. 子矩阵的和
Problem: 796. 子矩阵的和 文章目录 思路解题方法复杂度Code 思路 这是一个二维前缀和的问题。二维前缀和的主要思想是预处理出一个二维数组,使得每个位置(i, j)上的值表示原数组中从(0, 0)到(i, j)形成的子矩阵中所有元素的和。这样,对于任意的子矩阵(x…...

如何在 Python 中处理 Unicode
介绍 Unicode 是世界上大多数计算机的标准字符编码。它确保文本(包括字母、符号、表情符号,甚至控制字符)在不同设备、平台和数字文档中显示一致,无论使用的操作系统或软件是什么。它是互联网和计算机行业的重要组成部分…...

CSDN文章导出PDF整理状况一览
最近CSDN有了导出文章PDF功能,导出的PDF还可以查询, 因此,把文章导出PDF,备份一下自己的重要资料。 目前整理内容如下 No.文章标题整理时间整理之后 文章更新Size (M)10001_本地电脑-开发相关软件保持位…...
)
jmeter-05变量(用户定义变量,用户参数,csv文档参数化)
文章目录 一、jmeter有三种变量二、用户定义变量(这个更多的可以理解为全局变量)1、设置2、引用三、用户参数(可以理解为局部变量)1、设置2、引用3、用户参数化要配合线程组的线程数使用4、结果五、csv文档参数1、创建csv文件2、设置2、引用csv文件可以配合线程组的线程数,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
