DAY50:完全背包、爬楼梯、322、279
70 爬楼梯 (进阶)
爬楼梯问题在我们刚开始学习动态规划的时候作为入门的问题。当时题目考虑的是1或2种走法。如果将能走的台阶设为M,则能产生进阶的题目。通过求解完全背包问题得到。
题目如下:
题目页面
如果最多能走m个台阶,那么1,2,...,m种走法就是物品,走到楼顶就是背包。因为先走5再走1和先走1再走5是不一样的,因此这道题是排列问题,所以背包容量要放在循环外面。
- 递归公式 dp[i] += dp[i - j]
代码如下:
#include <iostream>
#include <vector>
using namespace std;
int main() {int n, m;while (cin >> n >> m) {vector<int> dp(n + 1, 0);dp[0] = 1;for (int i = 1; i <= n; i++) { // 遍历背包for (int j = 1; j <= m; j++) { // 遍历物品if (i - j >= 0) dp[i] += dp[i - j];}}cout << dp[n] << endl;}
}Leetcode: 322 零钱兑换
基本规律
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
基本思路
1、确定下标
dp[i]表示凑足总额为i所需钱币的最少个数为dp[j]
2、递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1,所以dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
3、初始化
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
这里涉及到一个代码的写法
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;4、循环逻辑
因为本题寻找的是最小,所以无关物品和背包的关系,为了代码好写,选择了外层for循环遍历物品,内层for遍历背包。
时间复杂度: O(n * amount)
空间复杂度: O(amount)
代码如下:
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for(int i = 0; i < coins.size(); i++){for(int j = coins[i]; j <= amount; j++){if(dp[j - coins[i]] != INT_MAX){dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};Leetcode: 279 完全平方数
1、下标和含义
dp[j]:和为j的完全平方数的最少数量为dp[j]
2、递推公式
和上题基本一样,只不过物品变成了平方数。
3、遍历顺序
遍历背包和物品都可以。
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for(int j = 0; j <= n; j++){//遍历背包for(int i = 1; i*i <= j; i++){//遍历物品,注意当小于背包容量的时候停止dp[j] = min(dp[j - i*i] + 1, dp[j]);}}return dp[n];}
};代码随想录
相关文章:

DAY50:完全背包、爬楼梯、322、279
70 爬楼梯 (进阶) 爬楼梯问题在我们刚开始学习动态规划的时候作为入门的问题。当时题目考虑的是1或2种走法。如果将能走的台阶设为M,则能产生进阶的题目。通过求解完全背包问题得到。 题目如下: 题目页面 如果最多能走m个台阶,…...
-缓存的优化与清理)
MySQL性能调优篇(3)-缓存的优化与清理
MySQL数据库缓存的优化与清理 数据库缓存在MySQL中扮演着非常重要的角色,它可以显著提高数据库的性能和响应速度。在本篇博客中,我们将介绍如何优化和清理MySQL数据库的缓存,以进一步提高数据库的效率。 优化缓存 1. 适当调整缓存大小 My…...

Zig、C、Rust的Pk1
Zig、C、Rust的Pk1 github.com上看到“A basic comparitive analysis of C, C, Rust, and Zig.”:https://github.com/CoalNova/BasicCompare/tree/main 里边的代码是9个月之前的,用现在的zig 0.11.0 及0.12-dev都无法通过编译(具体为:zig-w…...

如何用 ChatGPT 做项目管理?
ChatGPT 可以通过创建和维护跨团队项目协作计划,让员工更容易理解他们的角色和职责。 这个协作计划里面会包括每个团队或个人要执行的具体任务,每个任务最后期限和任何事情之 间的依赖关系。 该场景对应的关键词库:(24 个) 项目管理、项目协作计划、跨…...
DS:树及二叉树的相关概念
创作不易,兄弟们来波三连吧!! 一、树的概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,…...
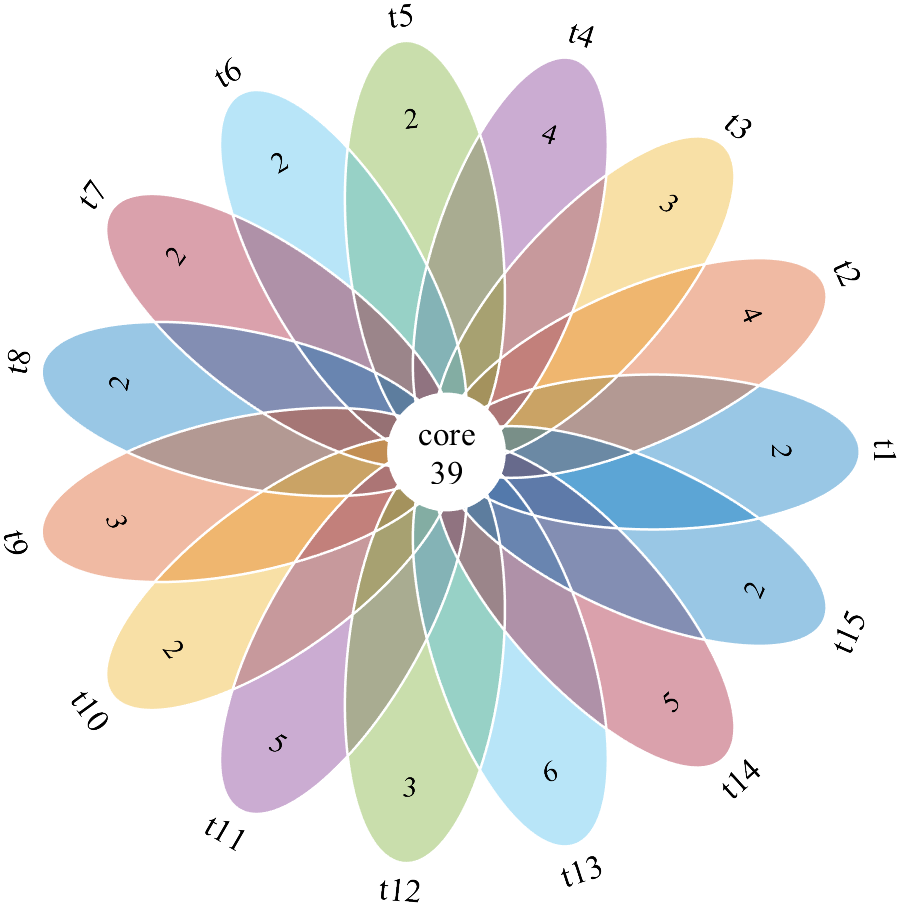
MATLAB | 情人节画个花瓣venn图?
之前七夕节情人节各种花,相册,爱心啥的都快画够了,今年画个花瓣韦恩图? 花瓣上的数字是仅属于该类的样本数,而中心的数字是属于每一类的样本数 教程部分 0 数据准备 % 给组起名t1 t2 t3...t15 setName compose(t%d,…...

[日常使用] Shell常用命令
Shell是什么? Shell简介 Shell是操作系统的外壳,是用户与操作系统内核之间的主要接口。它接收用户的命令并将其传递给内核执行,然后将执行结果返回给用户。Shell不仅是一个命令解释器,也是一种强大的编程语言。常见的Shell分为图…...
)
QT+OSG/osgEarth编译之八十七:osgdb_p3d+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_p3d)
文章目录 一、osgdb_p3d介绍二、文件分析三、pro文件四、编译实践一、osgdb_p3d介绍 P3DXML是Panda3D引擎中使用的一种文件格式,用于描述3D场景的层次结构和属性。它是一种基于XML(eXtensible Markup Language)的文本格式,可以被Panda3D引擎读取和解析。 P3DXML文件包含了…...
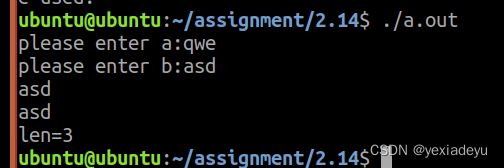
寒假 day13
1.请编程实现二维数组的杨慧三角 #include<stdio.h> #include<string.h> int main(int argc, const char *argv[]) { int n,i,j;printf("please enter n:");scanf("%d",&n);int arr[n][n];for(i0;i<n;i){for(j0;j<i;j){if(j0 || ij…...

探索微信小程序的奇妙世界:从入门到进阶
文章目录 一、什么是微信小程序1.1 简要介绍微信小程序的定义和特点1.2 解释小程序与传统应用程序的区别 二、小程序的基础知识2.1 微信小程序的架构2.2 微信小程序生命周期的理解2.3 探索小程序的目录结构和文件类型 三、小程序框架和组件3.1 深入了解小程序框架的核心概念和原…...
-std::forward_list)
容器库(4)-std::forward_list
std::forward_list是可以从任何位置快速插入和移除元素的容器,不支持快速随机访问,只支持正向迭代。 本文章的代码库: https://gitee.com/gamestorm577/CppStd 成员函数 构造、析构和赋值 构造函数 可以用元素、元素列表、迭代器或者另…...

Netty Review - 服务端channel注册流程源码解析
文章目录 PreNetty主从Reactor线程模型服务端channel注册流程源码解读入口 serverBootstrap.bind(port) 源码流程图 Pre Netty Review - ServerBootstrap源码解析 Netty Review - NioServerSocketChannel源码分析 Netty主从Reactor线程模型 Netty 使用主从 Reactor 线程模型…...

冒泡排序平均需要跑多少趟:拉马努金Q函数初探
摘要: 拉马努金Q函数在算法分析中的应用,初步体验 【对算法,数学,计算机感兴趣的同学,欢迎关注我哈,阅读更多原创文章】 我的网站:潮汐朝夕的生活实验室 我的公众号:算法题刷刷 我的知乎&#x…...
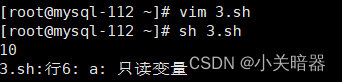
Shell 学习笔记(三)-shell变量
Shell 语言是一种动态类型和弱类型语言, 因此,在Shell中无需显示地声明变量, 且变量的类型会根据不同的操作符而发生变化. 静态类型语言: 在程序编译期间就确定变量类型的语言, 如java, C等 动态类型语言: 在程序运行期间才确定变量类型的语言, 如PHP, Python等. 一 shell变量…...

新冠:2022和2024两次新冠感染的对比
第一次 2022年底第一次放开管控,95%以上的人都感染了一次奥密克戎 症状 第一天:流涕,咽痛。 第二天:高烧40度,全身疼痛,动不了。没有胃口,头晕想吐。 吃了白加黑退烧药,清开灵颗粒…...

笔记:《NCT全国青少年编程能力等级测试教程Python语言编程二级》
NCT全国青少年编程能力等级测试教程Python语言编程二级 ISBN:9787302565857 绪论 专题1 模块化编程 考查方向 考点清单 考点 模块化编程 (一)模块化编程思想:结构清晰、降低复杂度;提高代码复用率;易于扩展、维护,方便阅读、优化。 …...

顶级思维方式——认知篇五(思想的觉醒)
目录 1、 女性的地位觉醒 2、电视剧《天道》之高人思维:丁元英为什么讲“人间黑白颠倒”? 3、 创业公司, 更应该大胆的创新. 4、 做到一定职务的时候, 你一定想到在你这个地位上你要做什么 1、 女性的地位觉醒 过去引以为鉴的例子&…...

面试技术栈 —— 2024网易雷火暑期实习真题
面试技术栈 —— 2024网易雷火暑期实习真题 1. 最长递增子序列。2. 集中限流和单机限流你觉得哪个好?3. redis部署服务器配置,为什么不用哨兵?4. 讲讲分布式session的原理。5. 数据库:表数据量大了,如何分表࿱…...
【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
我的成绩:小白(5/6) 完稿时间:2024-2-13 比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/ 相关资料: 1、出题人题解:“蓝桥杯双周赛第5次强者挑战赛/小白入门赛”出题人题解 - 知乎 (zhihu.com) 2、矩阵快速幂&…...
-yum二进制部署)
docker (二)-yum二进制部署
yum安装docker(Linux) 安装环境:CentOS 7.9 一 如果之前安装了旧版docker,请先删除 sudo yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
