【状态估计】深度传感器与深度估计算法(1/3)
深度传感器与深度估计算法
深度传感器概念
获得空间中目标位置或距离的传感器,按接收的媒介波来源可分为主动式和被动式两大范畴,主动式包括激光雷达、雷达、超声波传感器等,被动式主要为单目、多目相机等,同时两大类可组合为混合类型传感器,深度(即距离)测量机制可分为基于(被动)视差原理的机制和(主动)ToF(Time Of Flight)机制两种,使用结构光的RGBD相机,尽管其媒介波源于自身,但其工作原理实为双目视差。市面上已有面向室内应用的RGBD相机、面向自动驾驶应用的激光雷达+相机融合一体的传感器,其既有“被动测量深度”的单目或多目相机,又有“主动”测量深度的器件。由于环境信息规律的统一、不同种的媒介波的属性的统一,各式各样传感器的模型可再抽象为统一的深度传感器模型,进一步便引出了深度估计问题。
深度估计问题最早起源于双目立体视觉,后面扩展到多视图立体视觉并得到了详尽的研究可供借鉴,现在我们推广到一般的深度估计问题。
问题
自动驾驶应用为估计空间状态而使用多种具体的传感器,数据的具体处理方式不同,而此类硬件可被统一抽象为深度传感器,软件估计算法是否可以据此完成统一抽象?
首先总结问题的一般形式:已知传感器数据参考帧的位姿参数,帧上一个兴趣点的深度值和深度值方差的先验,提供帧序列和其位姿数据,通过一定方法获取相应同名点,估计该点的深度及其方差。此处深度指参考帧的坐标原点到空间点的距离。此问题需要设定深度分布的概率模型,然后给出一些参考思路。
深度传感器的概率模型
常用的概率模型有两种,第一种是高斯分布模型,较简单而易求解;第二种是高斯分布加均匀分布的混合分布,对现实传感器的属性描述更真实。高斯分布一般作为理想环境与传感器理想工作条件下传感器测量输出的分布,均匀分布则是对传感器运行异常或环境异常如遮挡问题等条件下假设的测量分布,两种分布的结合更能逼近描述真实世界。
深度求解的具体方法因特定传感器而异,下面首先以多视图图像估计深度为例给出具体估计方法,然后重点关注第二种概率模型的一般估计问题。
高斯分布模型的求解
深度期望估计
法I Triangulation求空间点坐标得出深度
x i x_{i} xi为图像点齐次坐标, P i P_i Pi为投影矩阵, X X X为空间点齐次坐标,投影方程如下,
x i = P i X x_i=P_iX xi=PiX
已知2帧以上的投影矩阵 P i P_i Pi和同名点,i=1,2……,求同名点的空间点估计X。
设 P j T P^{jT} PjT是 P i P_i Pi的第j行,则有
y p 3 T X − p 2 T X = 0 yp^{3T}X-p^{2T}X=0 yp3TX−p2TX=0
x p 3 T X − p 1 T X = 0 xp^{3T}X-p^{1T}X=0 xp3TX−p1TX=0
x p 2 T X − y p 1 T X = 0 xp^{2T}X-yp^{1T}X=0 xp2TX−yp1TX=0
第三行与前两行线性相关,利用多帧构造方程,
A X = 0 AX=0 AX=0
A的第i块为,
A i = [ y p 3 T − p 2 T x p 3 T − p 1 T ] A_i=\begin{bmatrix} yp^{3T}-p^{2T}\\xp^{3T}-p^{1T} \end{bmatrix} \quad Ai=[yp3T−p2Txp3T−p1T]
采用SVD求之。帧间运动不明显时易出现数值结果不稳定问题,实际测试中发现空间点坐标z经常为负数(以参考帧相机坐标系为参考坐标系,z应为正值),工程实现不考虑采用此法。
法II 射线法
设参考帧图像点对应一空间点的深度为 d r d_r dr,当前帧同一点的深度为 d c d_c dc, f r f_r fr, f c f_c fc分为参考帧、当前帧光心到空间点的射线单位矢量在相应帧坐标系下的表达,则有
d r f r = d c ( R r c f c ) + t r c d_rf_r=d_c(R_{rc}f_c)+t_{rc} drfr=dc(Rrcfc)+trc
令 f 2 = R r c f c f_2=R_{rc}f_c f2=Rrcfc, t = t r c t=t_{rc} t=trc,可构造如下方程,
[ f r T f r − f r T f 2 f 2 T f r − f 2 T f 2 ] [ d r d c ] = [ f r T t f 2 T t ] \begin{bmatrix} f^T_rf_r&-f^T_rf_2\\f^T_2f_r&-f^T_2f_2 \end{bmatrix} \quad\begin{bmatrix}d_r\\d_c\end{bmatrix}\quad=\begin{bmatrix}f^T_rt\\f^T_2t\end{bmatrix}\quad [frTfrf2Tfr−frTf2−f2Tf2][drdc]=[frTtf2Tt]
克莱默法则求解 d r d_r dr, d c d_c dc,获取参考帧下的光心到空间点下的矢量的两个表达式,
x m = d r f r x_m=d_rf_r xm=drfr
x n = d c f 2 + t x_n=d_cf_2+t xn=dcf2+t
取二者平均求结果模长即为新观测到的深度。
深度方差估计
考虑深度的不确定性,针对图像数据可考虑光度不确定性或几何不确定性,本文暂时只考虑几何关系造成的不确定性,假设角点观测误差为1个像素,以参考帧坐标系为参考系,设参考帧光心到当前帧光心的矢量为 t t t,参考帧光心到目标点的矢量为 p p p,当前帧光心到目标点的矢量为 a a a,
α = a r c c o s ( p ∗ t ∣ ∣ p ∣ ∣ ∗ ∣ ∣ t ∣ ∣ ) \alpha=arccos(\frac{p*t}{||p||*||t||}) α=arccos(∣∣p∣∣∗∣∣t∣∣p∗t)
β = a r c c o s ( a ∗ ( − t ) ∣ ∣ a ∣ ∣ ∗ ∣ ∣ t ∣ ∣ ) \beta=arccos(\frac{a*(-t)}{||a||*||t||}) β=arccos(∣∣a∣∣∗∣∣t∣∣a∗(−t))
β ′ = β + a r c t a n ( 1 / f ) \beta^\prime=\beta+arctan(1/f) β′=β+arctan(1/f)
γ = π − α − β ′ \gamma=\pi-\alpha-\beta^\prime γ=π−α−β′
∣ ∣ p ′ ∣ ∣ = ∣ ∣ t ∣ ∣ s i n β ′ s i n γ ||p^\prime||=||t||\frac{sin\beta^\prime}{sin\gamma} ∣∣p′∣∣=∣∣t∣∣sinγsinβ′
σ o b s = ∣ ∣ p ∣ ∣ − ∣ ∣ p ′ ∣ ∣ \sigma_{obs}=||p||-||p^\prime|| σobs=∣∣p∣∣−∣∣p′∣∣
σ o b s 2 = σ o b s ∗ σ o b s \sigma_{obs}^2=\sigma_{obs}*\sigma_{obs} σobs2=σobs∗σobs
相关文章:
)
【状态估计】深度传感器与深度估计算法(1/3)
深度传感器与深度估计算法 深度传感器概念 获得空间中目标位置或距离的传感器,按接收的媒介波来源可分为主动式和被动式两大范畴,主动式包括激光雷达、雷达、超声波传感器等,被动式主要为单目、多目相机等,同时两大类可组合为混…...
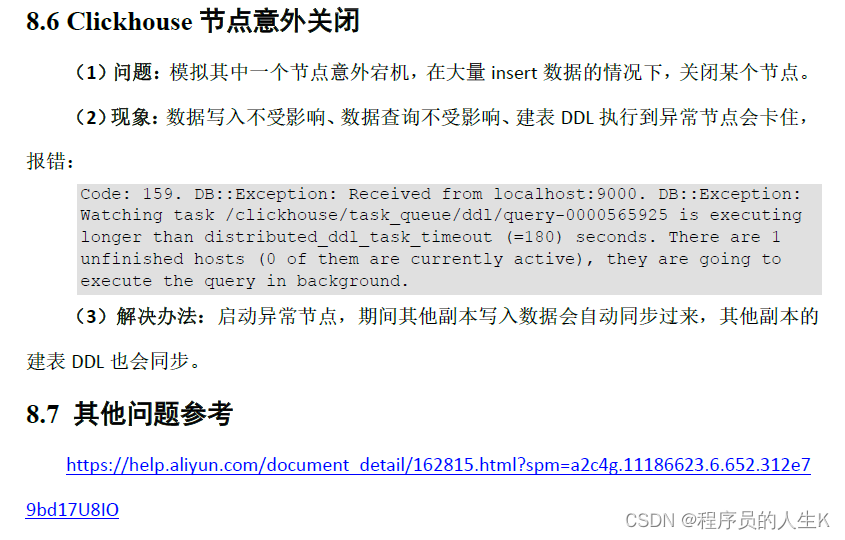
ClickHouse从入门到精通(高级)
第1章 Explain查看执行计划 第2章 建表优化 第3章 ClickHouse语法优化规则 第4章 查询优化 第5章 数据一致性(重点) 第6章 物化视图 第7章 MaterializeMySQL引擎 第8章 常见问题排查...

什么是Docker的容器编排工具,它们之间有何不同?
随着Docker容器技术的广泛应用,容器编排工具成为了自动化部署、扩展和管理容器化应用程序的关键组件。这些工具提供了一种抽象层,帮助开发者和管理员更高效地管理大量的Docker容器,确保它们在不同的主机和环境中能够可靠地运行。目前…...

qml之Control类型布局讲解,padding属性和Inset属性细讲
1、Control布局图 2、如何理解? *padding和*Inset参数如何理解呢? //main.qml import QtQuick 2.0 import QtQuick.Controls 2.12 import QtQuick.Layouts 1.12 import QtQuick.Controls 1.4 import QtQml 2.12ApplicationWindow {id: windowvisible: …...
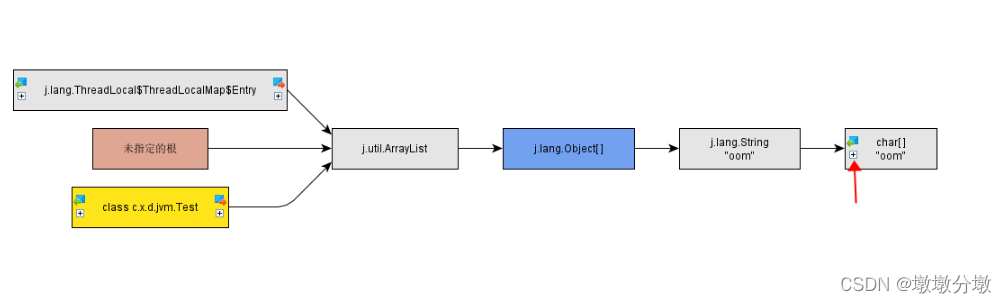
【Jvm】性能调优(拓展)Jprofiler如何监控和解决死锁、内存泄露问题
文章目录 Jprofiler简介1.安装及IDEA集成Jprofiler2.如何监控并解决死锁3.如何监控及解决内存泄露(重点)4.总结5.后话 Jprofiler简介 Jprofilers是针对Java开发的性能分析工具(免费试用10天), 可以对Java程序的内存,CPU,线程,GC,锁等进行监控和分析, 1.安装及IDEA集成Jprofil…...

运行错误(竞赛遇到的问题)
在代码提交时会遇见这样的错误: 此处运行错误不同于编译错误和答案错误,运行错误是指是由于在代码运行时发生错误,运行错误可能是由于逻辑错误、数据问题、资源问题等原因引起的。这些错误可能导致程序在运行时出现异常、崩溃。 导致不会显示…...

nodename nor servname provided, or not known
异常信息 在 Maven 打包过程中出现的 nodename nor servname provided, or not known 异常通常是由于 Maven 无法解析某个域名,这可能是因为网络问题、DNS 解析失败或者 Maven 配置中指定的仓库地址错误导致的。这个问题通常出现在 Maven 试图从远程仓库下载依赖时 …...

前端vue金额用逗号分隔
实现效果 代码 template部分 <el-input v-model"state.val"></el-input><div>{{ priceFor(state.val) }}</div> js部分 const state reactive({ val: });const priceFor (val)> {if(!val){return }else if(val.length<4){return…...
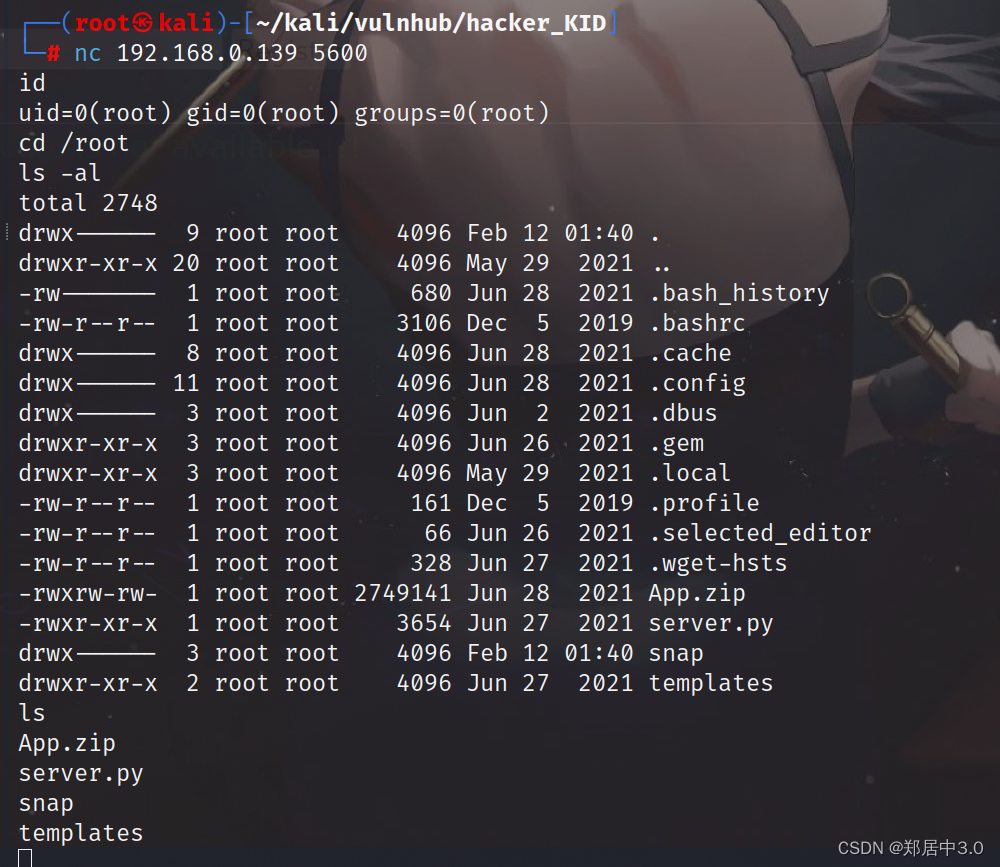
vulvhub-----Hacker-KID靶机
打靶详细教程 1.网段探测2.端口服务扫描3.目录扫描4.收集信息burp suite抓包 5.dig命令6.XXE漏洞读取.bashrc文件 7.SSTI漏洞8.提权1.查看python是否具备这个能力2.使用python执行exp.py脚本,如果提权成功,靶机则会开放5600端口 1.网段探测 ┌──(root…...
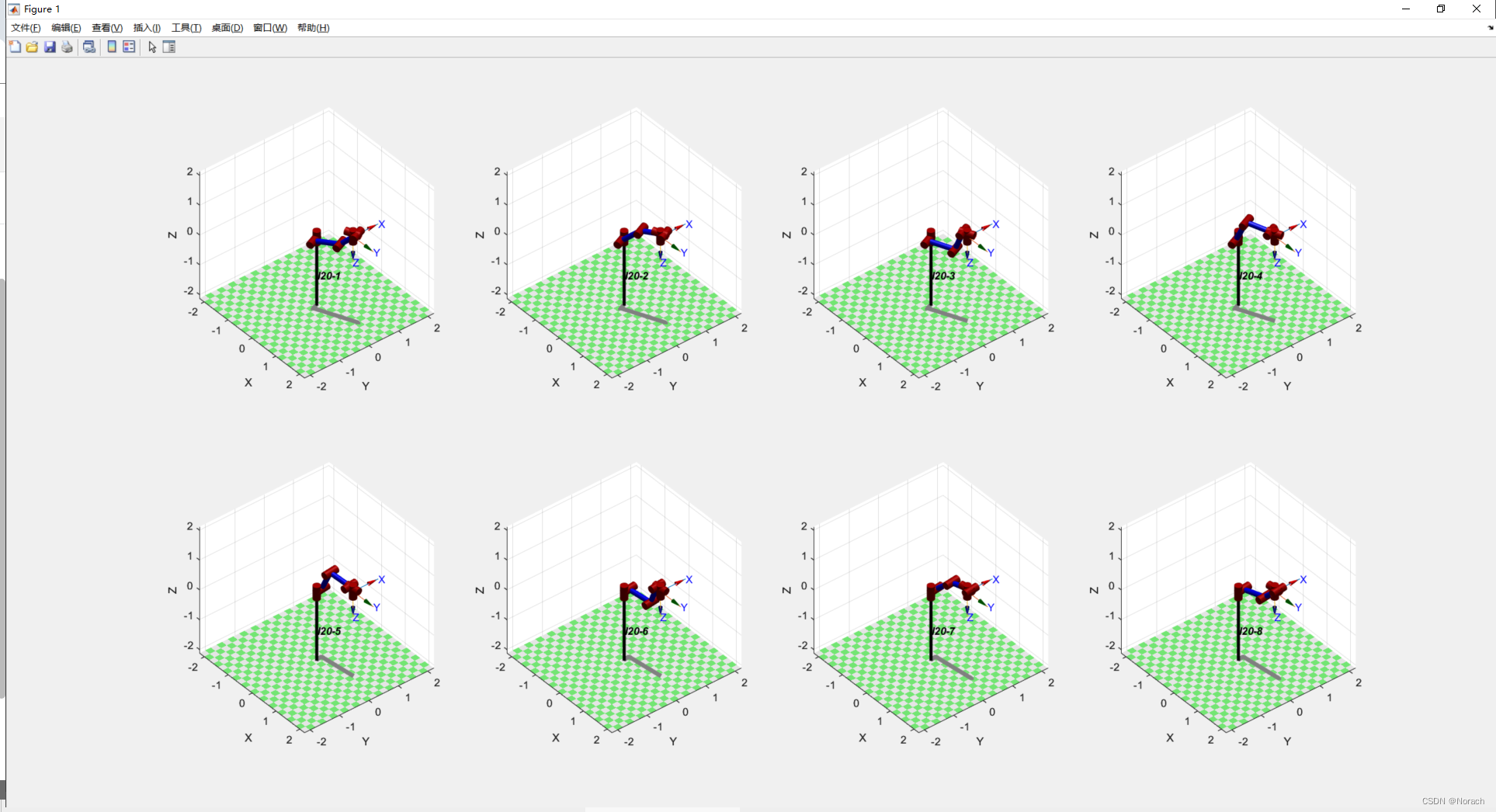
遨博I20协作臂关节逆解组Matlab可视化
AUBO I20协作臂关节逆解组Matlab可视化 前言1、RTB使用注意点2、代码与效果2.1、完整代码2.2、运行效果 总结 前言 注意:请预先配置好Matlab和RTB机器人工具箱环境,本文使用matlab2022b和RTB10.04版本 工作需要,使用matlab实现对六轴机械臂…...

力扣题目训练(15)
2024年2月8日力扣题目训练 2024年2月8日力扣题目训练507. 完美数520. 检测大写字母521. 最长特殊序列 Ⅰ221. 最大正方形237. 删除链表中的节点115. 不同的子序列 2024年2月8日力扣题目训练 2024年2月8日第十五天编程训练,今天主要是进行一些题训练,包括…...

PCB差模辐射是如何产生的
在电路应用中,高频时钟信号往往会采用差分线传输模式,其优点是在提高速率的同时减小功耗和提高抗扰度,因此,差模辐射就成为电路正常工作的结果,是电流流过导体形成的环路所产生,差模辐射模型可以被模拟为一个小环形天线,对于一个面积为A的小环路,载有电流Idm,在远场中…...
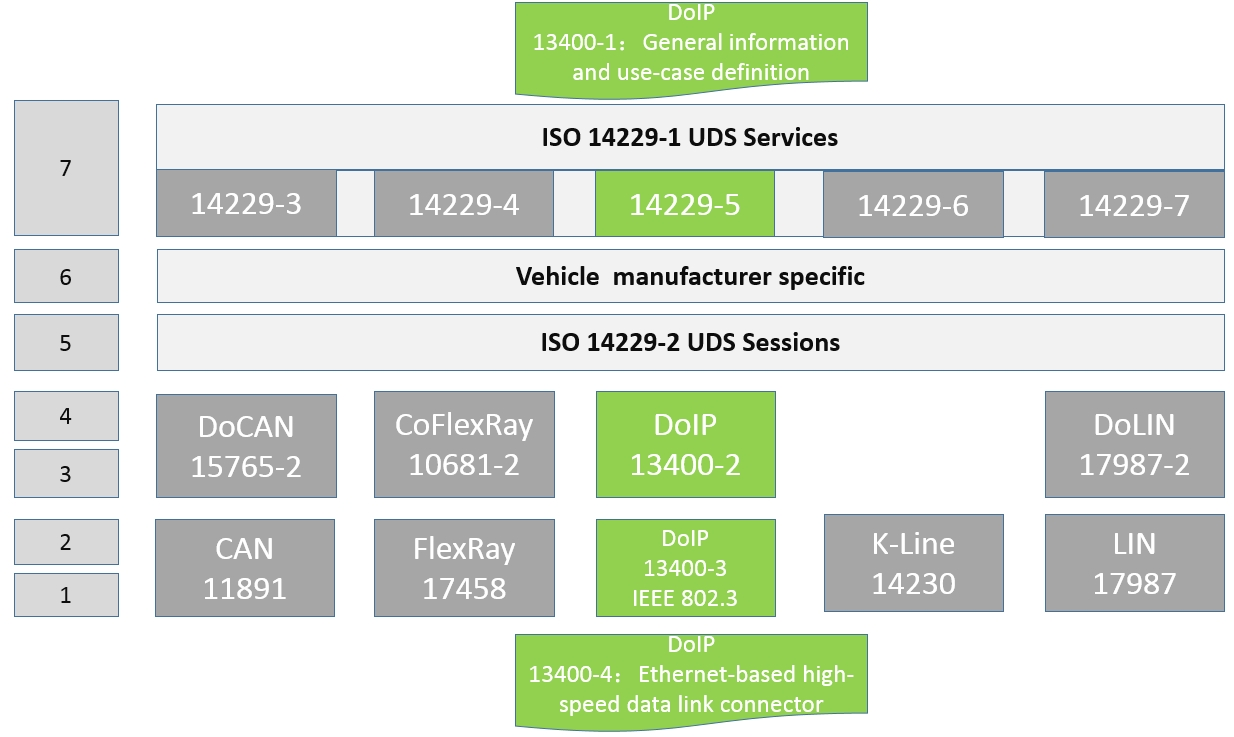
车载诊断协议DoIP系列 —— 协议中术语解释和定义
车载诊断协议DoIP系列 —— 协议中术语解释和定义 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,…...

【退役之重学前端】关于在控制台得到undefined的事
在浏览器控制台中,undefined 会时不时地,在我不想看到的地方出现。如果你遇到相同的问题,在这篇博客中你会得到答案。 先来看代码块 function test(){} test()//undefined再看下一个代码块 function test(){return 1; } test()//1再来看一个…...

指数和估计六大问题
1955年英国著名数学家R.A.Rankin在牛津大学出版的数学刊物Quart.J.Math.发表了论文(现 FRS D.R.Heath-Brown为主编),专门讲van der Corput方法产生的指数对理论(1933年E.Phillips提出的精彩理论,好友曲阜师范大学毕业中…...

【软件相关】基于Alist挂载云盘到本地文件资源管理器
文章目录 0 前言1 Alist挂载云盘2 RaiDrive配置3 rclone配置 0 前言 因为最近在研究各种云盘存储影视资源的方法,无意间看到一个教程是利用软件将云盘挂载到本地的资源管理器,这样就能实现类似本地文件操作的方式来操作云盘文件,还是有点意思…...

Java多线程系列——锁
0.引言 在并发编程中,锁是一种重要的同步机制,用于控制对共享资源的访问。Java 提供了多种锁的实现,每种锁都有不同的特性和适用场景。本文将深入介绍 Java 中常见的锁类型,包括内置锁、显式锁、读写锁等,并讨论它们的…...

蓝牙BLE学习-GAP
1.概述 GAP层(Generic access profile-通用访问配置文件)。GAP是对LL层payload(有效数据包)如何进行解析的两种方式的一种,而且也是最简单的一种。GAP简单的对LL payload进行一些规范和定义,因此GAP能实现的…...
, 贪心算法2)
算法训练营day28(补), 贪心算法2
//122. 买卖股票的最佳时机 II func maxProfit(prices []int) int { result : 0 //利润总和 for i : 1; i < len(prices); i { if prices[i]-prices[i-1] > 0 { result result (prices[i] - prices[i-1]) } } return result } //55. 跳跃游戏 func canJump(nums []…...
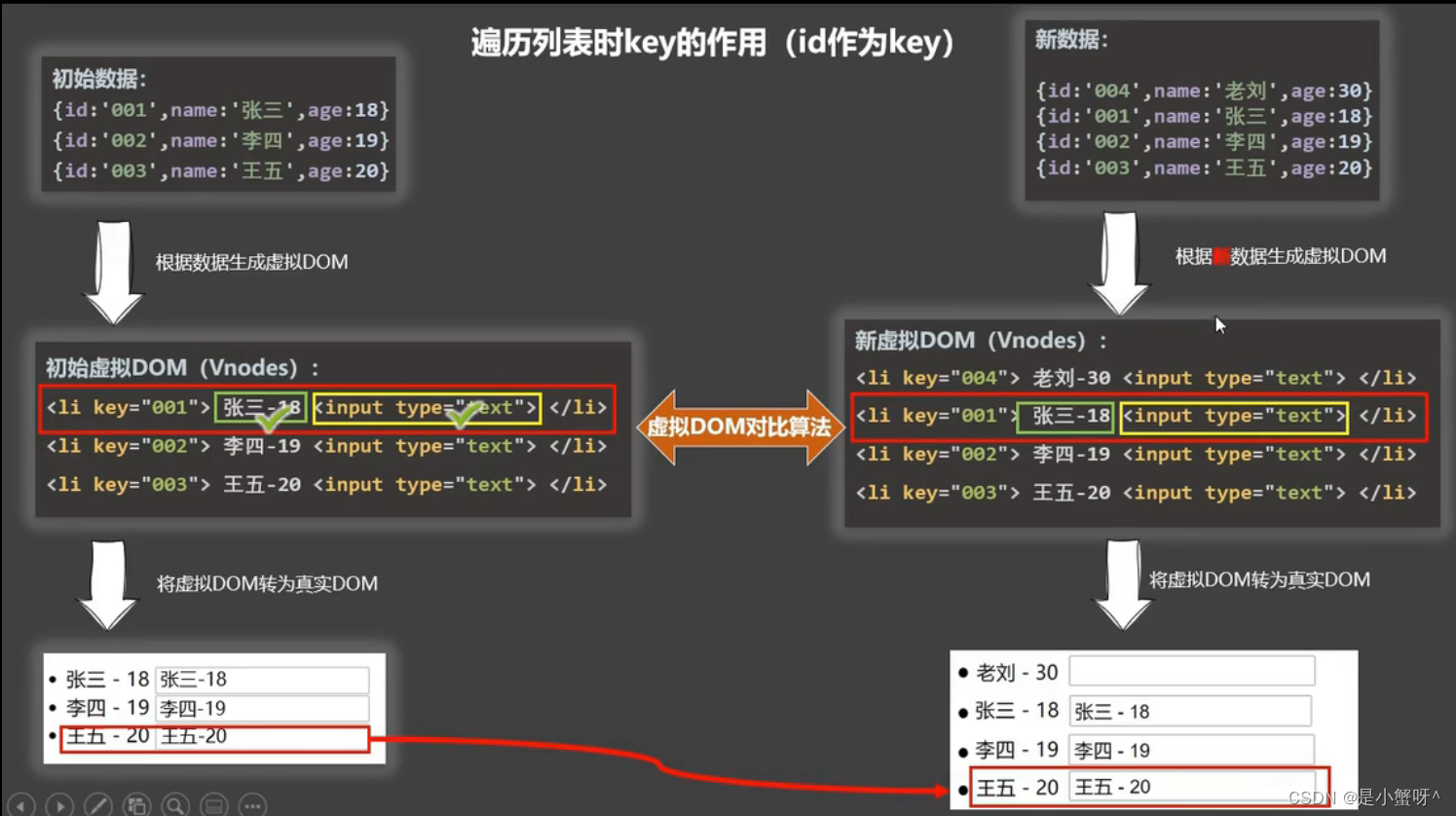
Vue核心基础4:绑定样式、条件渲染、列表渲染
1 绑定样式 【代码】 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>绑定样式</title><s…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
