龟兔赛跑算法
一、题目
给定一个长度为 n+1 的数组nums,数组中所有的数均在 1∼n1 的范围内,其中 n≥1。
请找出数组中任意一个重复的数。
样例
给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。返回 2 或 3。二、解析
解决这个问题的一种有效方法是使用快慢指针,也称为龟兔赛跑算法(Floyd's Cycle Detection Algorithm)。该算法的基本思想是在一个循环链表中,快指针和慢指针分别以不同的速度移动,如果存在环,则两者最终会相遇。
在这个问题中,可以将数组视为一个链表,数组中的元素值作为下一个节点的索引,构成一个链表。因为题目保证了数组中的元素值在 1 到 n 的范围内,所以数组中不存在负数,也不存在索引超出数组范围的情况。
原理:
当我们把数组中的元素看作链表中的节点时,题目要求找到数组中的任意一个重复数,实际上就是在链表中找到环的入口点。快慢指针算法的核心思想是利用两个不同速度的指针,如果存在环,这两个指针最终会相遇。
下面是算法的基本思路:
-
初始化:使用两个指针,一个慢指针
slow和一个快指针fast,初始时都指向数组的第一个元素nums[0]。 -
寻找相遇点:快指针每次前进两步,慢指针每次前进一步,直到两者相遇。相遇时,说明链表中存在环。
-
重置一个指针:将其中一个指针(例如慢指针)重置到数组的第一个元素
nums[0],而另一个指针保持在相遇点。 -
寻找环的入口点:两个指针再以相同速度前进,直到它们再次相遇。相遇点即为环的入口点,也即重复的数。
这个原理的关键在于,当两个指针相遇时,说明链表中存在环。在寻找环的入口点时,将一个指针重置到链表头,然后两个指针以相同的速度前进,它们再次相遇的点就是环的入口点。在这个问题中,环的入口点对应于数组中的重复数。
这个算法的时间复杂度为 O(n),其中 n 是数组的长度。算法的空间复杂度为 O(1),因为只使用了常数额外的空间。
下面是用C语言实现的代码:
#include <stdio.h>int findDuplicate(int* nums, int numsSize) {// 初始化快慢指针int slow = nums[0];int fast = nums[0];// 寻找相遇点do {slow = nums[slow];fast = nums[nums[fast]];} while (slow != fast);// 重置其中一个指针,并寻找环的入口点——这里可以想一想为什么:Aslow = nums[0];while (slow != fast) {slow = nums[slow];fast = nums[fast];}// 返回环的入口点,即重复的数return slow;
}int main() {// 示例用法int nums[] = {1, 3, 4, 2, 2};int numsSize = sizeof(nums) / sizeof(nums[0]);int duplicate = findDuplicate(nums, numsSize);printf("Duplicate: %d\n", duplicate);return 0;
}
A:让我们来解释一下为什么这个过程能找到环的入口点:
-
首次相遇点:当快指针和慢指针首次相遇时,它们分别走过的步数之间存在关系,快指针走过的步数是慢指针的两倍。假设两者相遇时,慢指针走了 k 步,则快指针走了 2k 步,其中 k 是环的长度的整数倍。
-
重置指针位置:将慢指针重置到数组的第一个元素
nums[0],保持快指针在相遇点不动。 -
再次相遇:此时,慢指针从数组头部开始,而快指针还停留在相遇点。它们以相同的速度前进,当慢指针再次走了 k 步时,快指针走了 2k 步,即正好走完了环的若干圈,同时再次相遇。
-
相遇点即为入口点:再次相遇的点就是环的入口点。这是因为在第一次相遇后,慢指针已经在环内走了若干圈,而重置后再次相遇时,慢指针还需走若干圈才能达到入口点,而快指针已经在环内等待,因此它们在入口点相遇。
这个过程的本质是根据快慢指针相遇时,快指针已经走过的步数是慢指针的两倍的特性,找到环的入口点。这个算法的关键在于数学上的推理,而实际上这种方法是基于龟兔赛跑算法的原理。
相关文章:

龟兔赛跑算法
一、题目 给定一个长度为 n1 的数组nums,数组中所有的数均在 1∼n1 的范围内,其中 n≥1。 请找出数组中任意一个重复的数。 样例 给定 nums [2, 3, 5, 4, 3, 2, 6, 7]。返回 2 或 3。 二、解析 解决这个问题的一种有效方法是使用快慢指针…...
Yii2项目使用composer异常记录
问题描述 在yii2项目中,使用require命令安装依赖时,出现如下错误提示 该提示意思是:composer运行时,执行了yiisoft/yii2-composer目录下的插件,但是该插件使用的API版本是1.0,但是当前的cmposer版本提供的…...

【蓝桥杯 2021】图像模糊
图像模糊 题目描述 小蓝有一张黑白图像,由 nm 个像素组成,其中从上到下共 n 行,每行从左到右 m 列。每个像素由一个 0 到 255 之间的灰度值表示。 现在,小蓝准备对图像进行模糊操作,操作的方法为: 对于…...

【leetcode】贪心算法介绍
详细且全面地分析贪心算法常用的解题套路、数据结构和代码逻辑如下: 找最值型: 每一步选择都是局部最优解,最后得到的结果就是全局最优解。常用于找零钱问题、区间覆盖问题等。一般情况下,可以通过排序将数据进行处理,…...
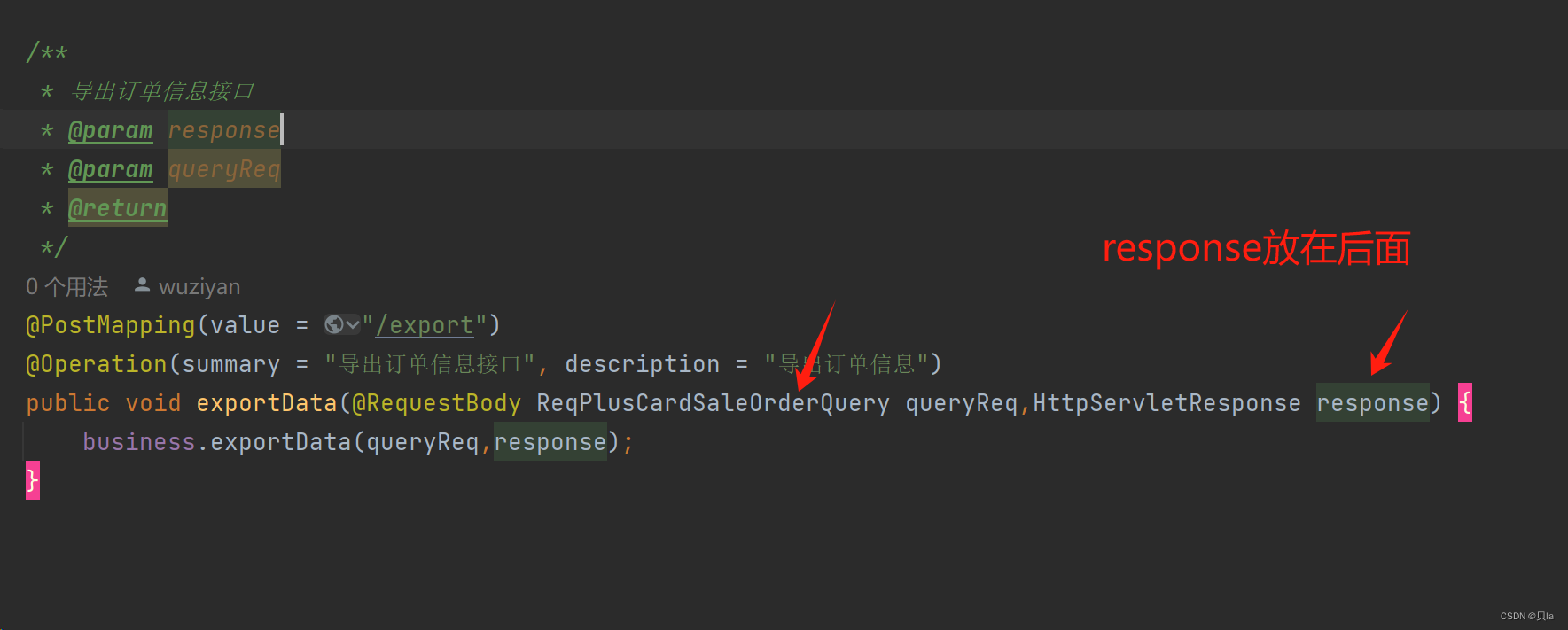
com.alibaba.fastjson.JSONException: toJSON error的原因
问题: 导出接口报错,显示json格式化异常 发现问题: 第一个参数为HttpResponse,转换成json的时候报错 修改方法: 1.调换两个参数的位置 2.在aop判断里边 把ServletAPI过滤掉 Before("excudeWebController()")pub…...
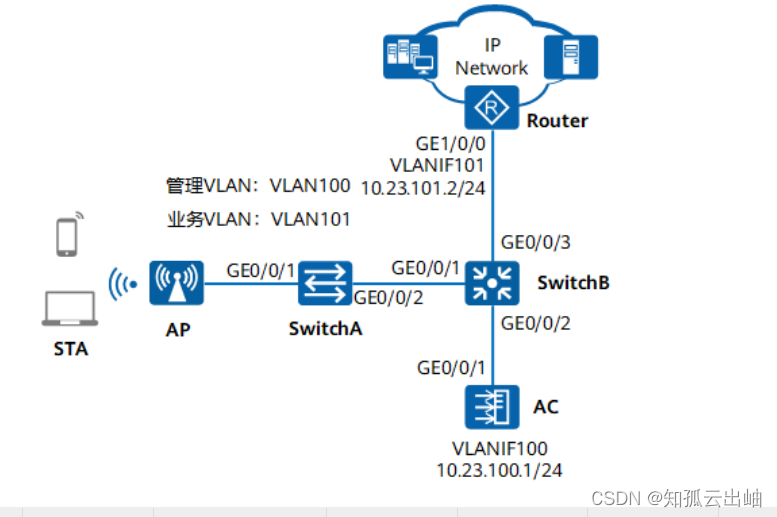
华为配置旁挂二层组网直接转发示例
配置旁挂二层组网直接转发示例 组网图形 图1 配置旁挂二层组网直接转发示例组网图 业务需求组网需求数据规划配置思路配置注意事项操作步骤配置文件扩展阅读 业务需求 企业用户通过WLAN接入网络,以满足移动办公的最基本需求。且在覆盖区域内移动发生漫游时ÿ…...

OLMo 以促进语言模型科学之名 —— OLMo Accelerating the Science of Language Models —— 全文翻译
OLMo: Accelerating the Science of Language Models OLMo 以促进语言模型科学之名 摘要 语言模型在自然语言处理的研究中和商业产品中已经变得无所不在。因为其商业上的重要性激增,所以,其中最强大的模型已经闭源,控制在专有接口之中&#…...

单例模式双端检测详解
正确写出doublecheck的单例模式_double check单例模式-CSDN博客...

秦PLUS荣耀版7.98万元起震撼上市,拉开“电比油低”大幕
2月19日,秦PLUS荣耀版正式上市,五大颠覆、三大焕新刷新A轿体验新高度。DM-i版本5款车型,官方指导价7.98万元——12.58万元;EV版本5款车型,官方指导价10.98万元——13.98万元。正式开启“电比油低”新时代。 电比油低&a…...

学习总结19
# 奶牛的耳语 ## 题目描述 在你的养牛场,所有的奶牛都养在一排呈直线的牛栏中。一共有 n 头奶牛,其中第 i 头牛在直线上所处的位置可以用一个整数坐标 pi(0< pi < 10^8) 来表示。在无聊的日子里,奶牛们常常在自己的牛栏里与其它奶牛交…...
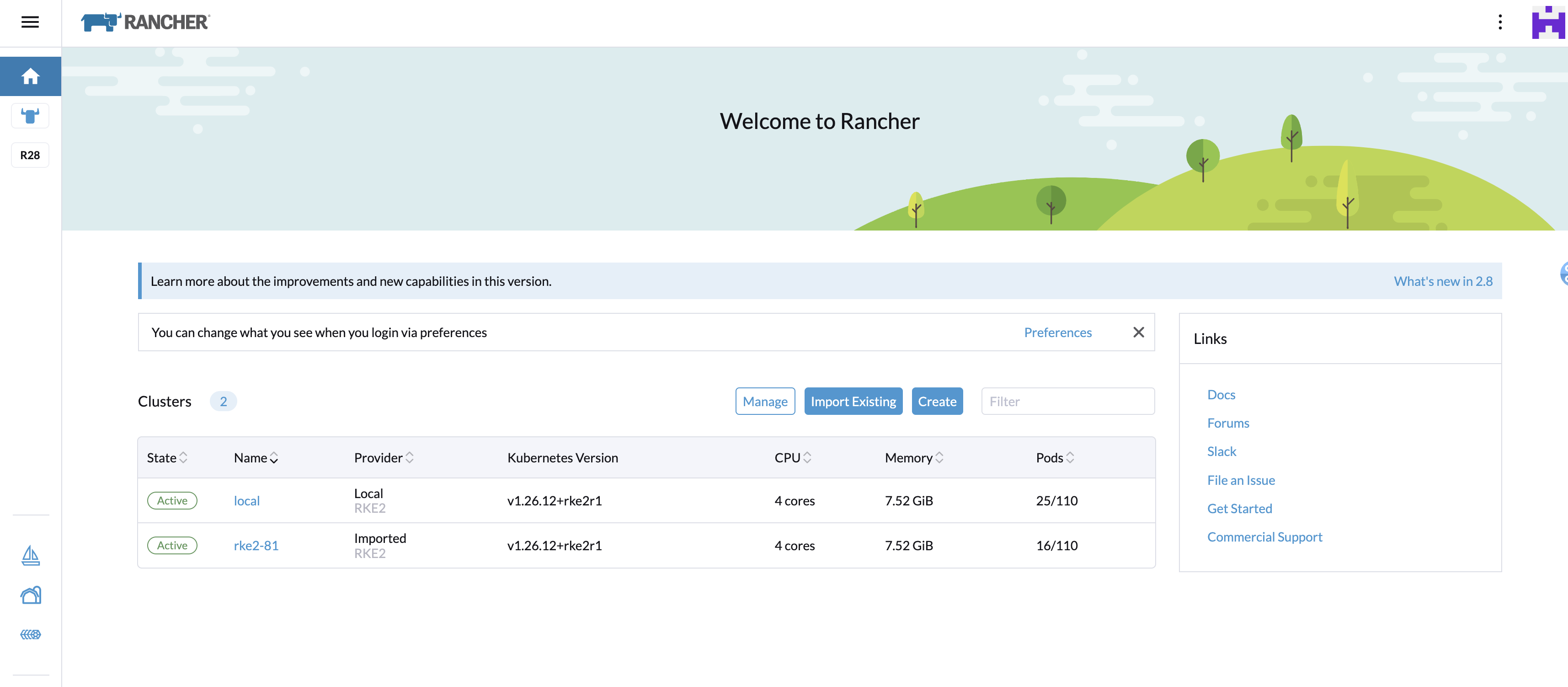
rancher v2.8.1 如何成功注册已有 k8s 集群
需要加入的集群为rke2部署的双节点集群 $ kubectl get node NAME STATUS ROLES AGE VERSION rke-master01 Ready control-plane,etcd,master,worker 94d v1.26.8rke2r1 rke-master02 Ready control-plane,etcd,mast…...

Vue中$root的使用方法
查看本专栏目录 关于作者 还是大剑师兰特:曾是美国某知名大学计算机专业研究生,现为航空航海领域高级前端工程师;CSDN知名博主,GIS领域优质创作者,深耕openlayers、leaflet、mapbox、cesium,canvas&#x…...

redis 异步队列
//produceMessage.ts 模拟生产者 import Redis from ioredis; const redis new Redis(); // 生产者:将消息推送到队列 async function produceMessage(queueName:string, message:string) {try {await redis.rpush(queueName, message);console.log(Produced messa…...

SpringBoot + Nacos 实现动态化线程池
1.背景 在后台开发中,会经常用到线程池技术,对于线程池核心参数的配置很大程度上依靠经验。然而,由于系统运行过程中存在的不确定性,我们很难一劳永逸地规划一个合理的线程池参数。 在对线程池配置参数进行调整时,一…...

《Docker极简教程》--Dockerfile--Dockerfile的基本语法
Dockerfile是一种文本文件,用于定义Docker镜像的内容和构建步骤。它包含一系列指令,每个指令代表一个构建步骤,从基础镜像开始,逐步构建出最终的镜像。通过Dockerfile,用户可以精确地描述应用程序运行环境的配置、依赖…...

css中, grid-auto-rows: 怎样简写在grid:中
grid-auto-rows:100px; grid-template-columns:1fr 1fr; 👆可以写成👇 grid:auto-flow 100px / 1fr 1fr;在CSS Grid布局中,grid-auto-rows 属性用于指定自动生成的网格容器的行的大小。如果你想要将 grid-auto-rows 的值简写在 grid 属性中&a…...
|Day53(动态规划))
@ 代码随想录算法训练营第8周(C语言)|Day53(动态规划)
代码随想录算法训练营第8周(C语言)|Day53(动态规划) Day50、动态规划(包含题目 ● 123.买卖股票的最佳时机III ● 188.买卖股票的最佳时机IV ) 123.买卖股票的最佳时机III 题目描述 给定一个数组 price…...

算法-矩阵置零
1、题目来源 73. 矩阵置零 - 力扣(LeetCode) 2、题目描述 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1…...
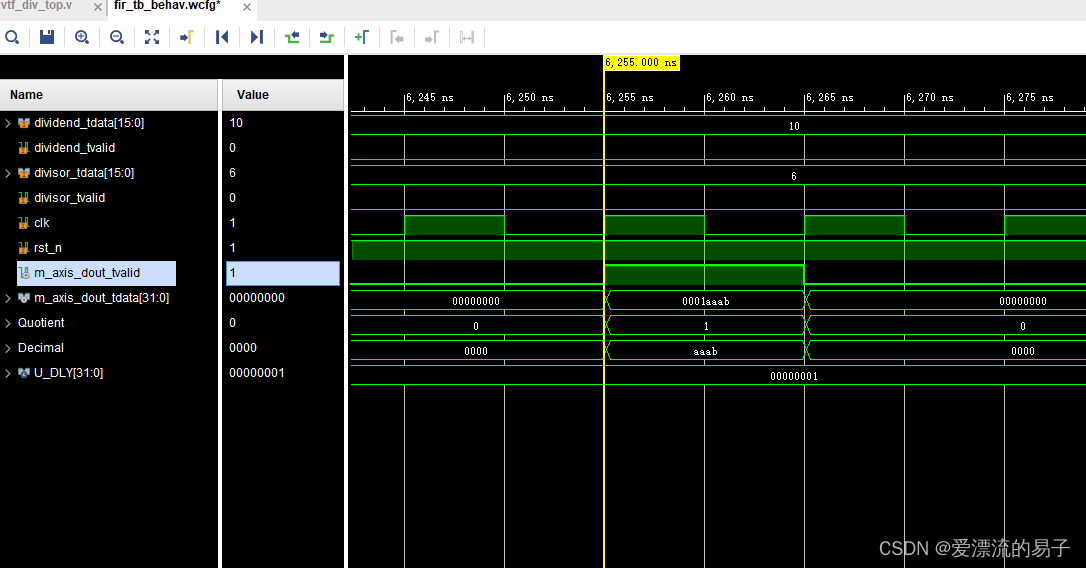
xilinx除法器的使用
平台:Vivado2018.3. 芯片:xcku115-flva1517-2-i (active) 最近学习使用了xilinx除法器,在使用过程中出现了很多次除法器的结果和我预计的结果不一致,特此记录学习一下。 参考文件:pg151.下载地址 pg151-div-gen.pdf …...
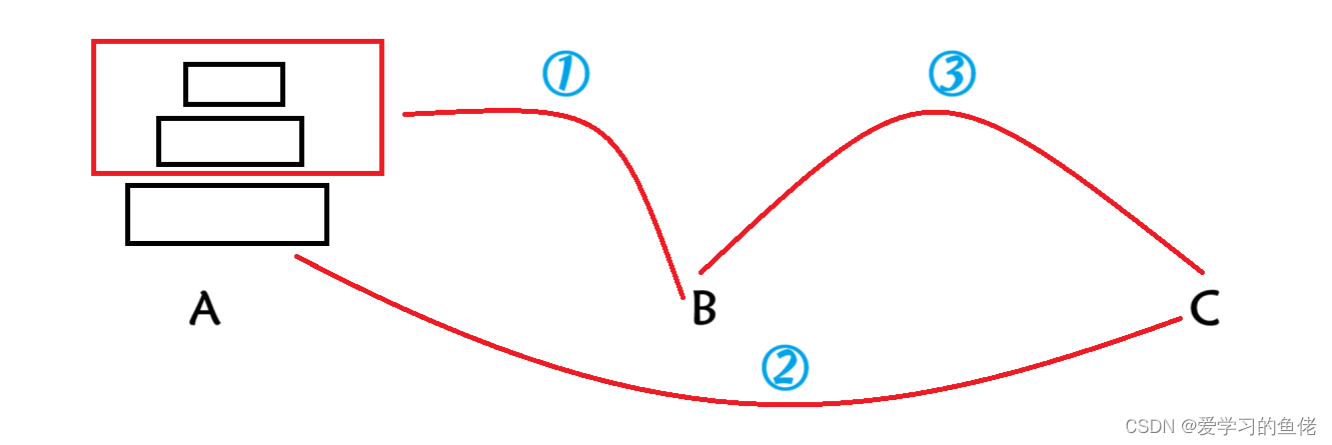
算法沉淀——递归(leetcode真题剖析)
算法沉淀——递归 01.汉诺塔问题02.合并两个有序链表03.反转链表04.两两交换链表中的节点05.Pow(x, n) 递归是一种通过调用自身的方式来解决问题的算法。在递归算法中,问题被分解为更小的相似子问题,然后通过对这些子问题的解进行组合来解决原始问题。递…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
